98. 验证二叉搜索树
给你一个二叉树的根节点
root,判断其是否是一个有效的二叉搜索树。有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:root = [2,1,3] 输出:true示例 2:
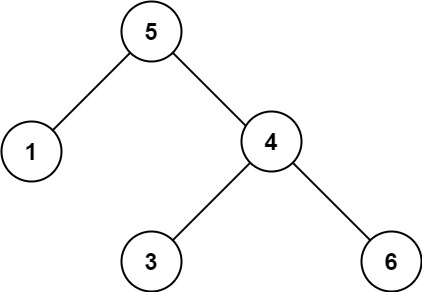
输入:root = [5,1,4,null,null,3,6] 输出:false 解释:根节点的值是 5 ,但是右子节点的值是 4 。提示:
- 树中节点数目范围在
[1, 104]内-231 <= Node.val <= 231 - 1
递归(通过形参改变取值范围):
class Solution {
public:bool func(TreeNode *root,long long lower,long long upper){if(root==nullptr)return true;if(root->val<=lower||root->val>=upper)return false;return func(root->left,lower,root->val)&&func(root->right,root->val,upper);}bool isValidBST(TreeNode* root) {return func(root,LONG_MIN,LONG_MAX);}
};递归(中序遍历)(通过比较当前节点值和上一个节点值):
中序遍历是左中右的顺序,刚刚好搜索二叉树的特点是左<中<右。
class Solution {
public:TreeNode *pre=nullptr;bool isValidBST(TreeNode* root) {if(root==nullptr)return true;bool left=isValidBST(root->left);if(pre!=nullptr&&pre->val>=root->val)return false;pre=root;bool right=isValidBST(root->right);return left&&right;}
};相关文章:
98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。 有效 二叉搜索树定义如下: 节点的左子树只包含 小于 当前节点的数。节点的右子树只包含 大于 当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。 示例 1: 输入&am…...

Stream API
Stream API执行流程 Stream API(java.util.stream)把真正的函数式编程风格引入到Java中,可以极大地提高程序员生产力,让程序员写出高效、简洁的代码 实际开发中项目中多数数据源都是来自MySQL、Oracle等关系型数据库,还有部分来自MongDB、Redis等非关系型数据库 …...

手写Spring:第3章-实现Bean的定义、注册、获取
文章目录 一、目标:实现Bean的定义、注册、获取二、设计:实现Bean的定义、注册、获取三、实现:实现Bean的定义、注册、获取3.1 工程结构3.2 实现Bean的定义、注册、获取类图3.3 定义Bean异常3.4 BeanDefinition定义和注册3.4.1 BeanDefinitio…...

这些国外客户真直接
最近在某平台上遇到的客户,很大一部分都是非英语国家的客户,然而他们也有很多共性的习惯。 第一种:直接表达自己对这个产品感兴趣,然后接下来就没有下文了,而之所以可以看得懂,则是借助平台本身的翻译系统&…...
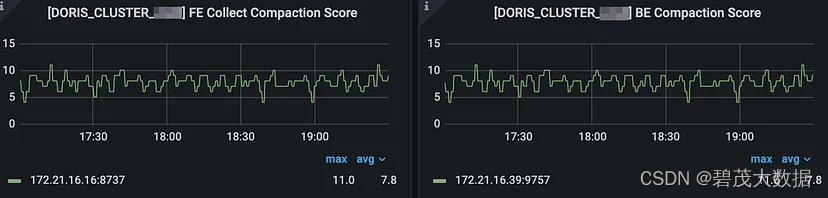
使用Apache Doris自动同步整个 MySQL/Oracle 数据库进行数据分析
Flink-Doris-Connector 1.4.0 允许用户一步将包含数千个表的整个数据库(MySQL或Oracle )摄取到Apache Doris(一种实时分析数据库)中。 通过内置的Flink CDC,连接器可以直接将上游源的表模式和数据同步到Apache Doris&…...
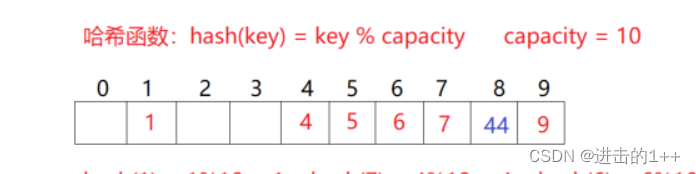
【1++的数据结构】之哈希(一)
👍作者主页:进击的1 🤩 专栏链接:【1的数据结构】 文章目录 一,什么是哈希?二,哈希冲突哈希函数哈希冲突解决 unordered_map与unordered_set 一,什么是哈希? 首先我们要…...
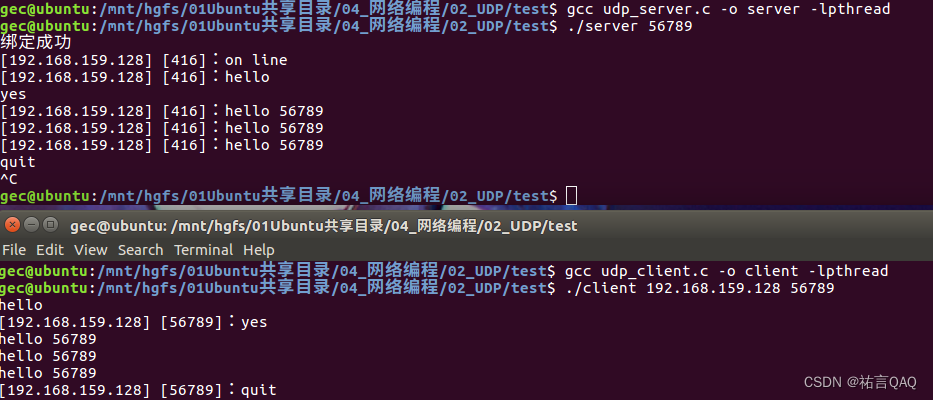
【网络编程】深入了解UDP协议:快速数据传输的利器
(꒪ꇴ꒪ ),Hello我是祐言QAQ我的博客主页:C/C语言,数据结构,Linux基础,ARM开发板,网络编程等领域UP🌍快上🚘,一起学习,让我们成为一个强大的攻城狮࿰…...
WordPress(5)在主题中添加文章字数和预计阅读时间
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 样式图一、添加位置二、找到主题文件样式图 提示:以下是本篇文章正文内容,下面案例可供参考 一、添加位置 二、找到主题文件 在主题目录下functions.php文件把下面的代码添加进去: // 文章字数…...
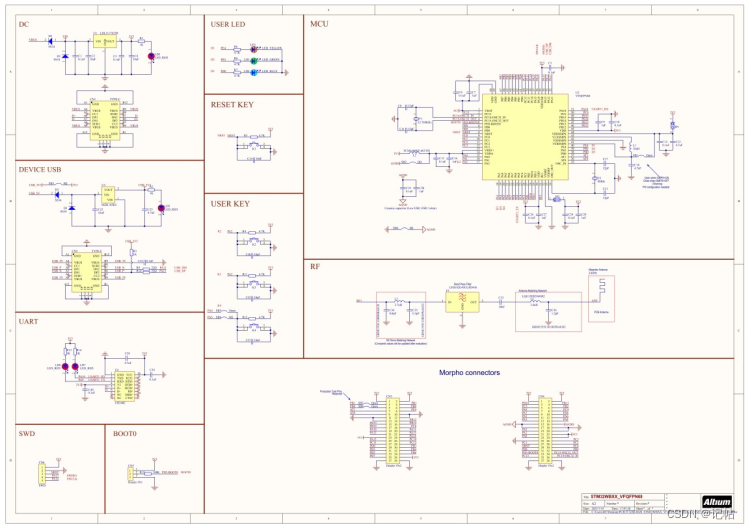
STM32WB55开发(1)----套件概述
STM32WB55开发----1.套件概述 所用器件视频教学样品申请优势支持协议系统控制和生态系统访问功能示意图系统框图跳线设置开发板原理图 所用器件 所使用的器件是我们自行设计的开发板,该开发板是基于 STM32WB55 系列微控制器所构建。STM32WBXX_VFQFPN68 不仅是一款评…...

CUDA相关知识科普
显卡 显卡(Video card,Graphics card)全称显示接口卡,又称显示适配器,是计算机最基本配置、最重要的配件之一。就像电脑联网需要网卡,主机里的数据要显示在屏幕上就需要显卡。因此,显卡是电脑进…...

恒运资本:总市值和总资产区别?
总市值和总财物是财政术语中经常被提到的两个概念,很多人会将它们混淆。在金融领域中,了解这两个概念的差异十分重要。本文将从多个视点深入分析总市值和总财物的差异。 1.定义 总市值是指公司发行的一切股票的商场总价值。所谓商场总价值…...

CTF安全竞赛介绍
目录 一、赛事简介 二、CTF方向简介 1.Web(Web安全) (1)简介 (2)涉及主要知识 2.MISC(安全杂项) (1)介绍 (2)涉及主要知识 3…...

DC/DC开关电源学习笔记(四)开关电源电路主要器件及技术动态
(四)开关电源电路主要器件及技术动态 1.半导体器件2.变压器3.电容器4.功率二极管5.其他常用元件5.1 电阻5.2 电容5.3 电感5.4 变压器5.5 二极管5.6 整流桥5.7 稳压管5.8 绝缘栅-双极性晶体管1.半导体器件 功率半导体器件仍然是电力电子技术发展的龙头, 电力电子技术的进步必…...
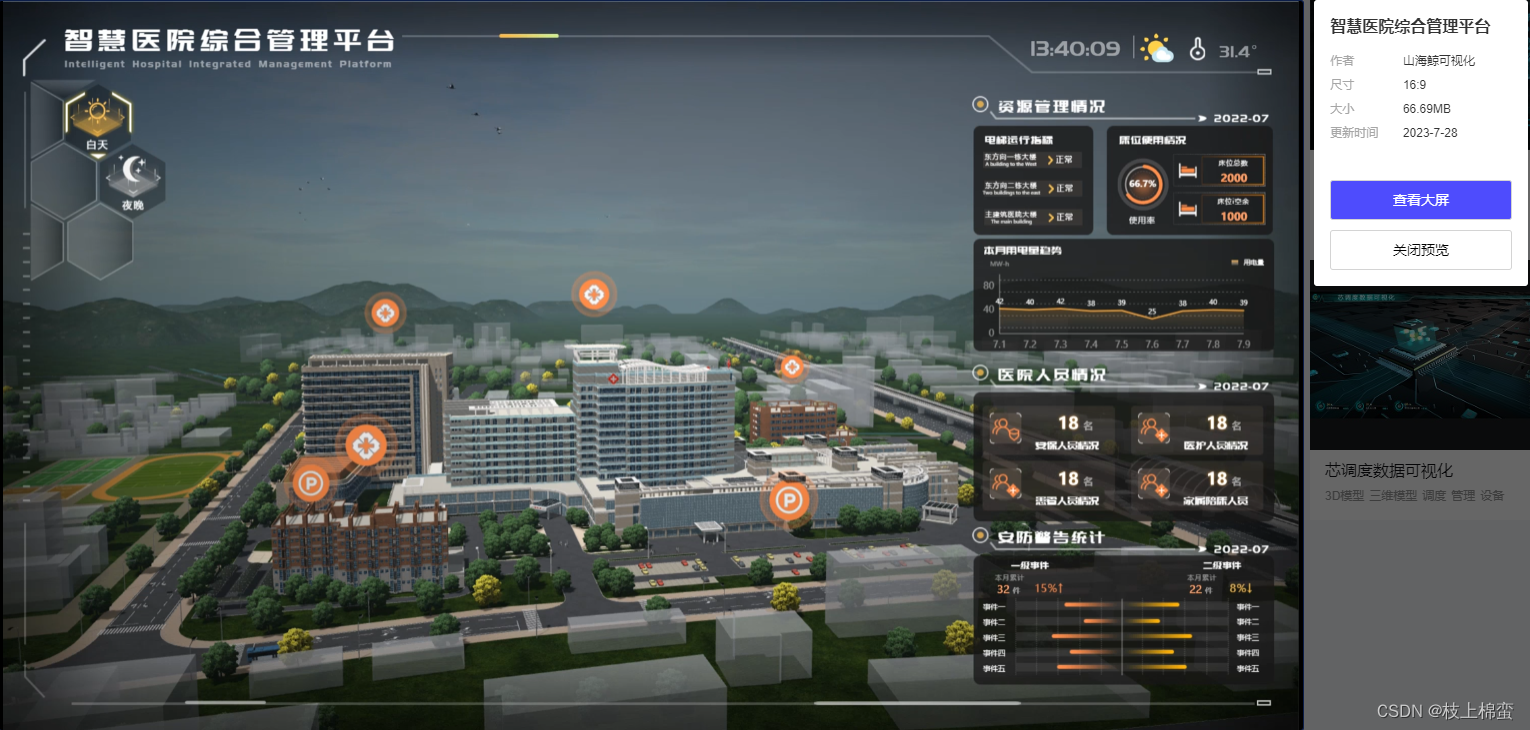
数据可视化与数字孪生:理解两者的区别
在数字化时代,数据技术正在引领创新,其中数据可视化和数字孪生是两个备受关注的概念。尽管它们都涉及数据的应用,但在本质和应用方面存在显著区别。本文带大探讨数据可视化与数字孪生的差异。 概念 数据可视化: 数据可视化是将复…...
)
C++ socket编程(TCP)
服务端保持监听客户端, 服务端采用select实现,可以监听多个客户端 客户端源码 在这里插入代码片 #include <iostream> //#include <windows.h> #include <WinSock2.h> #include <WS2tcpip.h> using namespace std; #pragma co…...

ldd用于打印程序或库文件所依赖的共享库列表
这是一个Linux命令行指令,将两个常用的命令 ldd 和 grep 组合使用。我来逐一为您解释: ldd: 这是一个Linux工具,用于打印程序或库文件所依赖的共享库列表。通常,当你有一个可执行文件并且想知道它链接到哪些动态库时,你…...
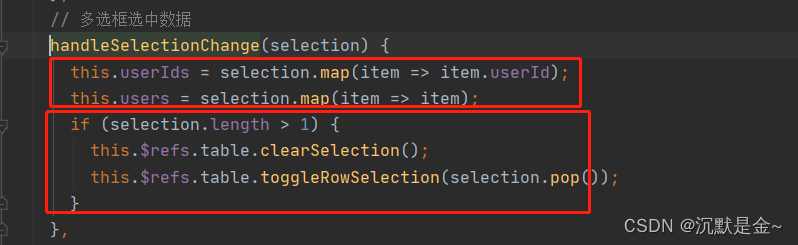
vue+elementUI el-table实现单选
if (selection.length > 1) {this.$refs.table.clearSelection();this.$refs.table.toggleRowSelection(selection.pop());}...
前端组件库造轮子——Message组件开发教程
前端组件库造轮子——Message组件开发教程 前言 本系列旨在记录前端组件库开发经验,我们的组件库项目目前已在Github开源,下面是项目的部分组件。文章会详细介绍一些造组件库轮子的技巧并且最后会给出完整的演示demo。 文章旨在总结经验,开…...
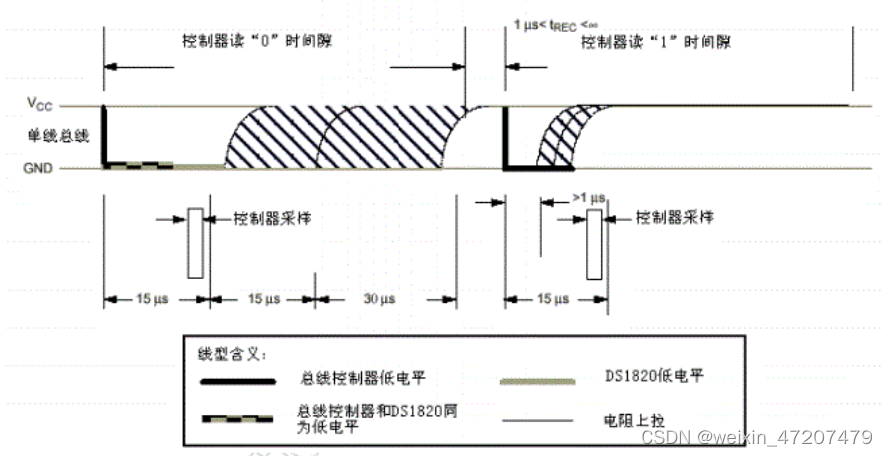
单片机第二季:温度传感器DS18B20
目录 1,DS18B20介绍 2,DS18B20数据手册 2.1,初始化时序 2.2,读写时序 3,DS18B20工作流程 4,代码 1,DS18B20介绍 DS18B20的基本特征: (1)内置集成ADC,外部数字接…...

抓包工具fiddler的基础知识
目录 简介 1、作用 2、使用场景 3、http报文分析 3.1、请求报文 3.2、响应报文 4、介绍fiddler界面功能 4.1、AutoResponder(自动响应器) 4.2、Composer(设计请求) 4.3、断点 4.4、弱网测试 5、app抓包 简介 fiddler是位于客户端和服务端之间的http代理 1、作用 监控浏…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

