day55 补
392.判断子序列
力扣题目链接(opens new window)
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
示例 1:
- 输入:s = "abc", t = "ahbgdc"
- 输出:true
示例 2:
- 输入:s = "axc", t = "ahbgdc"
- 输出:false
提示:
- 0 <= s.length <= 100
- 0 <= t.length <= 10^4
两个字符串都只由小写字符组成。
#算法公开课
《代码随想录》算法视频公开课 (opens new window):动态规划,用相似思路解决复杂问题 | LeetCode:392.判断子序列 (opens new window),相信结合视频再看本篇题解,更有助于大家对本题的理解。
#思路
(这道题也可以用双指针的思路来实现,时间复杂度也是O(n))
这道题应该算是编辑距离的入门题目,因为从题意中我们也可以发现,只需要计算删除的情况,不用考虑增加和替换的情况。
所以掌握本题的动态规划解法是对后面要讲解的编辑距离的题目打下基础。
动态规划五部曲分析如下:
- 确定dp数组(dp table)以及下标的含义
dp[i][j] 表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。
注意这里是判断s是否为t的子序列。即t的长度是大于等于s的。
有同学问了,为啥要表示下标i-1为结尾的字符串呢,为啥不表示下标i为结尾的字符串呢?
为什么这么定义我在 718. 最长重复子数组 (opens new window)中做了详细的讲解。
其实用i来表示也可以!
但我统一以下标i-1为结尾的字符串来计算,这样在下面的递归公式中会容易理解一些,如果还有疑惑,可以继续往下看。
- 确定递推公式
在确定递推公式的时候,首先要考虑如下两种操作,整理如下:
- if (s[i - 1] == t[j - 1])
- t中找到了一个字符在s中也出现了
- if (s[i - 1] != t[j - 1])
- 相当于t要删除元素,继续匹配
if (s[i - 1] == t[j - 1]),那么dp[i][j] = dp[i - 1][j - 1] + 1;,因为找到了一个相同的字符,相同子序列长度自然要在dp[i-1][j-1]的基础上加1(如果不理解,在回看一下dp[i][j]的定义)
if (s[i - 1] != t[j - 1]),此时相当于t要删除元素,t如果把当前元素t[j - 1]删除,那么dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了,即:dp[i][j] = dp[i][j - 1];
其实这里 大家可以发现和 1143.最长公共子序列 (opens new window)的递推公式基本那就是一样的,区别就是 本题 如果删元素一定是字符串t,而 1143.最长公共子序列 是两个字符串都可以删元素。
- dp数组如何初始化
从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1],所以dp[0][0]和dp[i][0]是一定要初始化的。
这里大家已经可以发现,在定义dp[i][j]含义的时候为什么要表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。
因为这样的定义在dp二维矩阵中可以留出初始化的区间,如图:

如果要是定义的dp[i][j]是以下标i为结尾的字符串s和以下标j为结尾的字符串t,初始化就比较麻烦了。
dp[i][0] 表示以下标i-1为结尾的字符串,与空字符串的相同子序列长度,所以为0. dp[0][j]同理。
vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
1
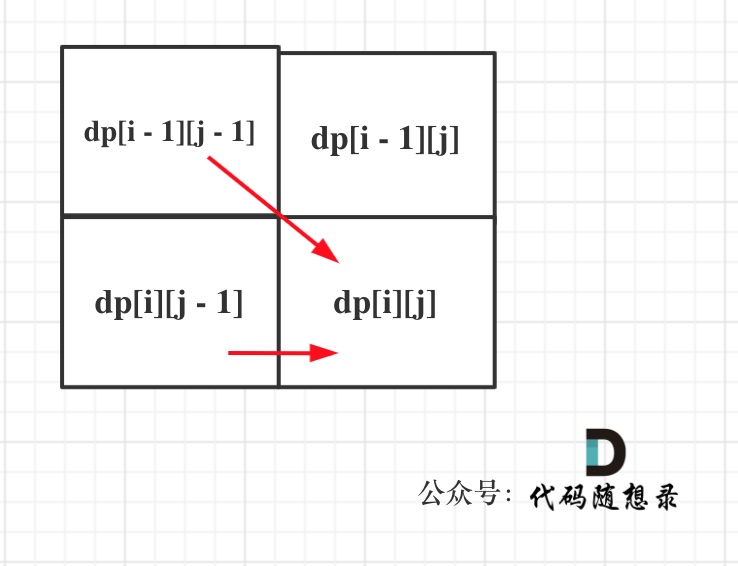
- 确定遍历顺序
同理从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1],那么遍历顺序也应该是从上到下,从左到右
如图所示:
- 举例推导dp数组
以示例一为例,输入:s = "abc", t = "ahbgdc",dp状态转移图如下:
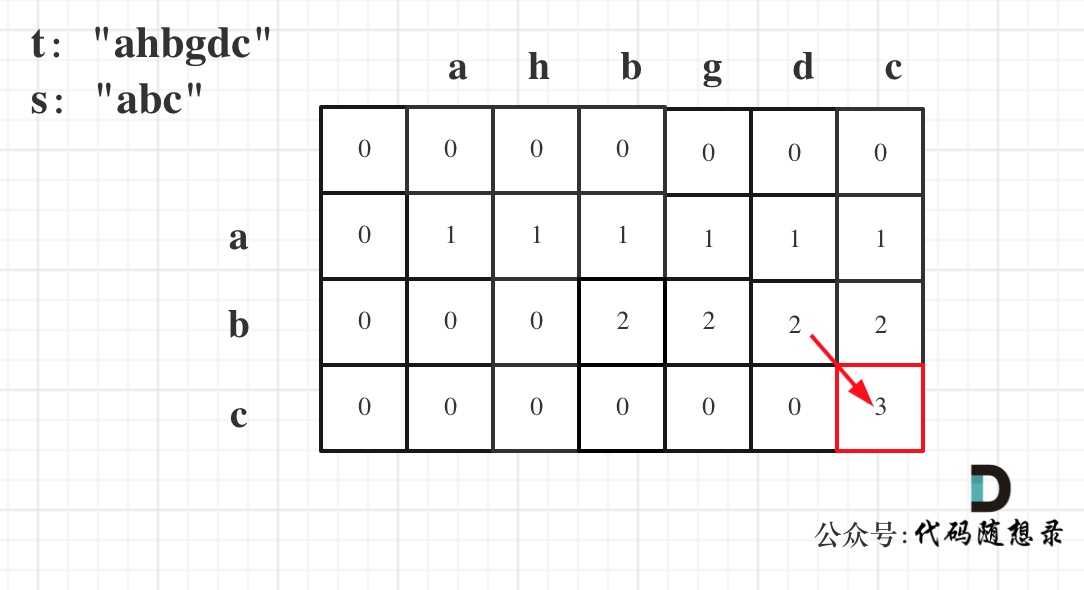
dp[i][j]表示以下标i-1为结尾的字符串s和以下标j-1为结尾的字符串t 相同子序列的长度,所以如果dp[s.size()][t.size()] 与 字符串s的长度相同说明:s与t的最长相同子序列就是s,那么s 就是 t 的子序列。
图中dp[s.size()][t.size()] = 3, 而s.size() 也为3。所以s是t 的子序列,返回true。
动规五部曲分析完毕,C++代码如下:
class Solution {
public:bool isSubsequence(string s, string t) {vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));for (int i = 1; i <= s.size(); i++) {for (int j = 1; j <= t.size(); j++) {if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = dp[i][j - 1];}}if (dp[s.size()][t.size()] == s.size()) return true;return false;}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
- 时间复杂度:O(n × m)
- 空间复杂度:O(n × m)
#总结
这道题目算是编辑距离的入门题目(毕竟这里只是涉及到减法),也是动态规划解决的经典题型。
这一类题都是题目读上去感觉很复杂,模拟一下也发现很复杂,用动规分析完了也感觉很复杂,但是最终代码却很简短。
在之前的题目讲解中,我们讲了 1143.最长公共子序列 (opens new window),大家会发现 本题和 1143.最长公共子序列 的相似之处。
编辑距离的题目最能体现出动规精髓和巧妙之处,大家可以好好体会一下。
#其他语言版本
#Java:
class Solution {public boolean isSubsequence(String s, String t) {int length1 = s.length(); int length2 = t.length();int[][] dp = new int[length1+1][length2+1];for(int i = 1; i <= length1; i++){for(int j = 1; j <= length2; j++){if(s.charAt(i-1) == t.charAt(j-1)){dp[i][j] = dp[i-1][j-1] + 1;}else{dp[i][j] = dp[i][j-1];}}}if(dp[length1][length2] == length1){return true;}else{return false;}}
}相关文章:

day55 补
392.判断子序列 力扣题目链接(opens new window) 给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,&quo…...
函数的应用——动态修改样式 root的使用)
CSS变量之var()函数的应用——动态修改样式 root的使用
一、css变量 body {--foo: #7F593F;--urls: ./img/xxx.jpg; }变量的名称可以用数字、汉字等,不能包含**$,[,^,(,%**等字符,变量的值也是可以使用各种属性值: 如: // 定义css变量 :r…...

索尼 toio ™应用创意开发征文|一个理想的绘画小助手
引言 toio™机器人是索尼推出的一款创意玩具,它的小巧和可编程性使其成为一个理想的绘画助手。通过编程控制机器人的运动和绘画工具,我们可以为小朋友提供一个有趣的绘画体验。 创意描述 我们可以通过JavaScript编程来控制toio™机器人的运动和绘画工具…...

java加密,使用python解密 ,使用 pysm4 报 byte greater than 16的解决方法
1,业务需要,对方需要用java进行参数加密,双方约定使用的加密方法是 SM4,对方给的key是32位,并且给出了加解密的java代码。 import org.bouncycastle.jce.provider.BouncyCastleProvider; import java.security.Key; i…...

django后台启动CORS跨越配置
文章目录 背景什么是跨域问题?跨域问题的解决方案 Django 解决跨域问题 背景 什么是跨域问题? 跨域问题是指浏览器的同源策略限制了来自不同域的 AJAX 请求。 具体来说: 同源策略要求源相同才能正常进行 AJAX 通信。判断是否同源需要满足三个条件: 协…...

异常的顶级理解
目录 1.异常的概念与体系结构 1.1异常的体系结构 1.2异常的举例 1.3错误的举例 2.异常的分类 2.1编译时异常 2.2运行时异常 3.异常的处理 3.1异常的抛出throw 3.2try-catch捕获并处理 3.3finally 3.4 异常声明throws 4.自定义异常类 1.异常的概念与体系结构 1.1异常的…...
LinkedHashMap实现LRU缓存cache机制,Kotlin
LinkedHashMap实现LRU缓存cache机制,Kotlin LinkedHashMap的accessOrdertrue后,访问LinkedHashMap里面存储的元素,LinkedHashMap就会把该元素移动到最尾部。利用这一点,可以设置一个缓存的上限值,当存入的缓存数理超过…...
)
Google 开源库Guava详解(集合工具类)
任何具有JDK Collections Framework经验的程序员都知道并喜欢java.util.Collections.Guava提供了更多的实用程序:适用于所有集合的静态方法。这些是番石榴最受欢迎和成熟的部分。 对应于特定接口的方法以相对直观的方式分组: nterface JDK or Guava? …...
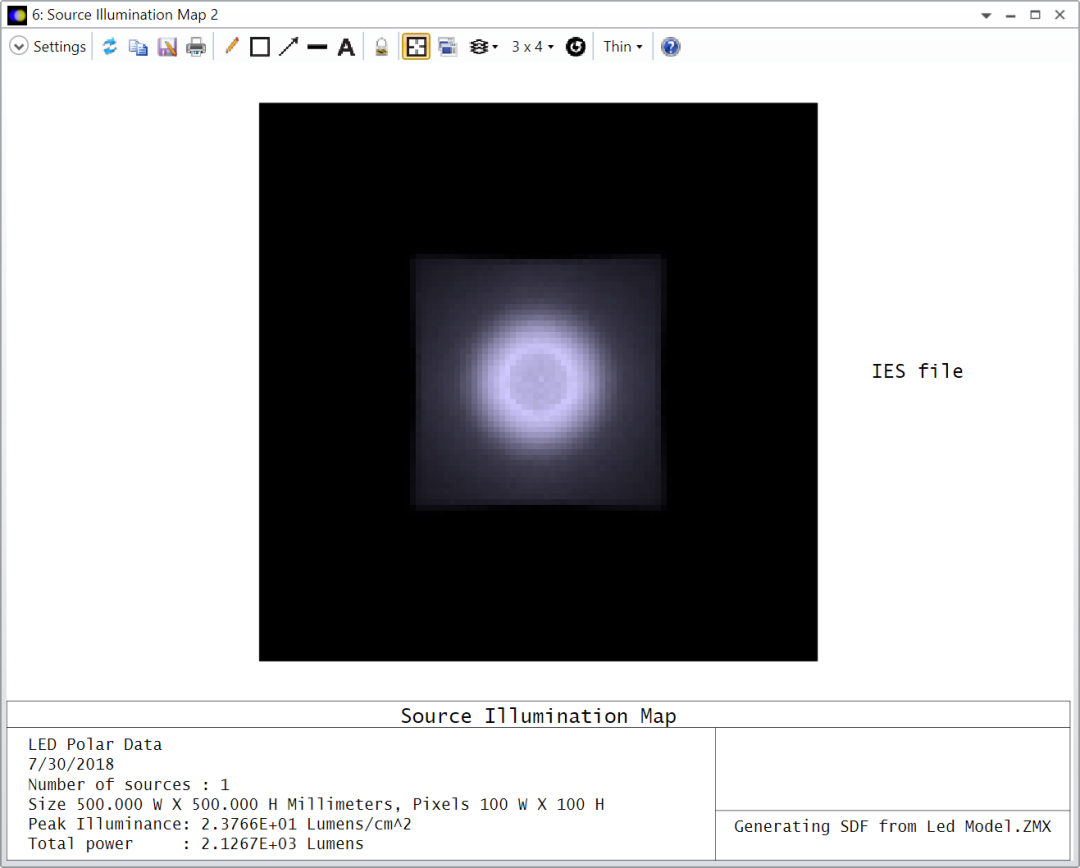
Ansys Zemax | 如何将光线追迹结果导出为IES格式
照明系统设计者通常需要向客户提供IES格式的数据。照明工程学会 (Illuminating Engineering Society,IES) 文件格式便于传输辉度数据,该格式得到了制造商和设计师的广泛认可。本文描述了如何生成IES文件并验证结果。(联系我们获取文章附件&am…...

JSONObject 比 Map好使的地方
需求:改originalJson中的json字符串的key,当key满足在configMapping中配置的key2情况的时候,把originalJson的key改成 configMapping中的value2。 上代码: import cn.hutool.json.JSONArray; import cn.hutool.json.JSONObject;p…...
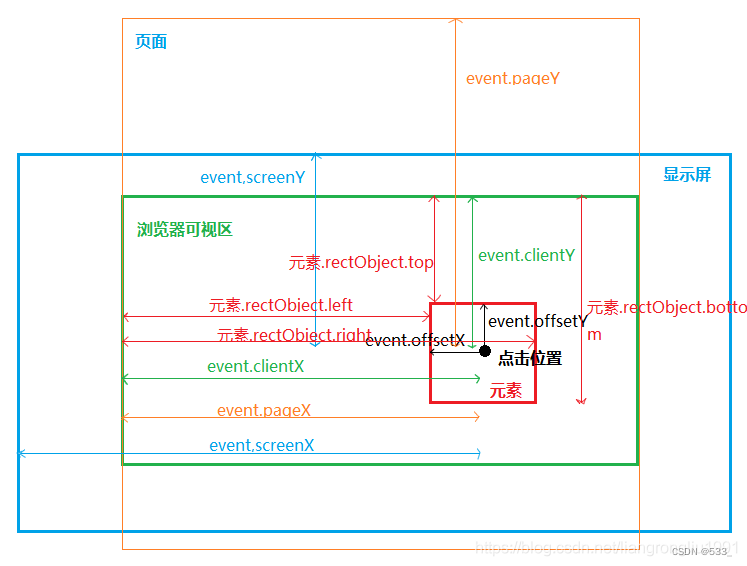
[js] 图解 event.pageX event.clientX event.offsetX getBoundingClientRect
event.clientX、event.clientY 鼠标相对于浏览器窗口可视区域的X,Y坐标(窗口坐标),可视区域不包括工具栏和滚动条。IE事件和标准事件都定义了这2个属性 event.pageX、event.pageY 类似于event.clientX、event.clientY,…...

VsCode备忘
上次简单学习了一下vscode的使用,结果好长时间没用,今天打开又全忘了。。。再记录一下吧 快捷键 CtrlShiftP 命令面板,查找命令,设置等等 Ctrl 打开集成终端,监视生成输出 Ctrl, 打开设置 CtrlP 转到文件,使用转到符…...

Linux命令200例:Yum强大的包管理工具使用(常用)
🏆作者简介,黑夜开发者,CSDN领军人物,全栈领域优质创作者✌。CSDN专家博主,阿里云社区专家博主,2023年6月csdn上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师࿰…...
使用 Linux 相关知识部署博客系统
目录 编辑一、认识 Linux 二、如何拥有 Linux 环境 三、常见的 Linux 命令 1、目录相关命令 (1)ls (2)pwd (3)cd 2、文件操作相关命令 (1)touch (2…...
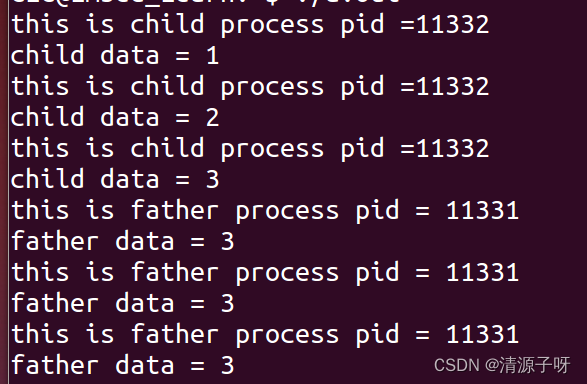
Linux--进程--vfork与fork区别
vfork: 所需头文件:#include <sys/types.h> #include <unistd.h> pid_t vfork(void); 功能: vfork() 函数和 fork() 函数一样都是在已有的进程中创建一个新的进程,但它们创建的子进程是有区别的。 参数ÿ…...

Ubuntu系统重装nvidia gpu驱动
1. 卸载原驱动 sudo apt remove *cuda* sudo apt remove *nvidia* sudo /usr/bin/nvidia-uninstall sudo dpkg -l | grep ^rc | cut -d -f3 | sudo xargs dpkg --purge sudo rm -rf ~/.cuda-license-* sudo apt purge nvidia-cuda-toolkit sudo apt remove nvidia-driver-* s…...

Java + Selenium + Appium自动化测试
一、启动测试机或者Android模拟器(Genymotion俗称世界上最快的模拟器,可自行百度安装) 二、启动Appium(Appium环境安装可自行百度) 三、安装应用到Genymotion上,如下图我安装一个计算机的小应用ÿ…...

【sgLazyCascader】自定义组件:基于el-cascader的懒加载级联菜单,支持异步加载子级菜单
sgLazyCascader源码 <template><div :class"$options.name"><el-cascader :props"props" v-model"model" :placeholder"placeholder || 请选择" :options"options"></el-cascader></div> &l…...
2023高教社杯数学建模E题思路模型 - 黄河水沙监测数据分析
# 1 赛题 E 题 黄河水沙监测数据分析 黄河是中华民族的母亲河。研究黄河水沙通量的变化规律对沿黄流域的环境治理、气候变 化和人民生活的影响, 以及对优化黄河流域水资源分配、协调人地关系、调水调沙、防洪减灾 等方面都具有重要的理论指导意义。 附件 1 给出了位…...

一、Linux下常用的压缩格式
一、Linux下常用的压缩格式 Linux下常用的压缩扩展名有:.tar、.tar.bz2、.tar.gz。 二、Windows下7ZIP软件的安装 因为Linux下很多文件是.bz2,.gz结尾的压缩文件,因此需要在windows下安装7ZIP软件。 三、gzip压缩工具 .gzip工具负…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...
