2023年高教社杯数学建模国赛 赛题浅析
2023年国赛如期而至,为了方便大家尽快确定选题,这里将对赛题进行浅析,以分析赛题的主要难点、出题思路以及选择之后可能遇到的难点进行说明,方便大家尽快确定选题。
难度排序 B>A>C
选题人数 C>A>B (预估结果,详细结果需要8号统计之后才可以公布)
A 题 定日镜场的优化设计
A题符合国赛A题的常规出题套路,以定日镜场为命题背景,设置物理相关的赛题。问题一需要根据 题目给出的的相关计算公式、相关数据计算年平均光学效率、年平均输出热功率,以及单位镜面面积年平均输出热功率等。属于物理计算问题,难度不算太大,中等。需要消耗不小的时间弄明白公式后,进行计算。这种问题对于结果的精度要求通常不低,结果的分数设置大概为每个结果5分,三个结果一共15分,问题一设置25-30分的总分,一半的分值由结果确定。
问题二、三经典的优化问题,以年平均输出热功率最大为目标函数,构建优化模型。吸收塔的位置坐标、定日镜尺寸、安装高度、位置坐标等数据作为决策变量进行设置。问题二的约束条件逐句翻译题干即可,(额定功率限制、定日镜尺寸及安装高度等限制)
问题三,引入定日镜尺寸可以不同,安装高度也可以不同。因此引入新的约束构建模型即可。主要难点在于约束条件的寻找构建以及优化模型的求解。

B 题 多波束测线问题
B题一改往届国赛B题的常规出题套路,以多波束测为背景,设置与物理相关的赛题。这种题设是近十年都没有出现过的方式。因此,难度也是最大的一道题目。问题一、构建覆盖宽度及相邻条带之间重叠率的数学模型,问题二构建多波束测深覆盖宽度的数学模型。这种模型的构建需要对题目有了很深的理解之后,再结合相应的物理知识才能进行构建,具有很强的专业性,因此不太建议新手、实力不强的队伍选择,很容易就会碰壁。
问题三、四,相当于实际应用,利用问题一二构建的模型,计算一种实际情。
整体来看,B题是本次比赛最难的一道题目,对参赛队员的专业素养、知识储备都是很大的考验。因此,希望大家慎重抉择。
C 题 蔬菜类商品的自动定价与补货决策
C题的命题与以往常规国赛C题命题相近,数据处理分析+优化问题。以蔬菜销售为背景设置相关的命题。数据类题目第一步一定是数据处理, 如此庞大的数据集,一定是存在异常值缺失值等情况,需要我们进行查找判定。通常对于这一部分,最后是设有分值的大概是5-10分左右,一定要进行处理!!!!!
问题一、分析分布规律及相互关系。切记是两个问题,分布规律和相关关系。分布规律,绘制相应的散点图加上文字描述即可。相关关系,属于评价模型的一种,隶属关联分析,大家可以参考下图进行选择合适的方法即可。

问题二、三优化模型,三要素目标函数、决策变量、约束条件。对应的翻译题干,寻找约束条件构建即可
问题2 最值问题求解 优化问题(六大类)
目标函数 收益
决策变量 日补货总量
约束条件 等式关系
不等式关系
问题3 最值问题求解 优化问题(251小品)
目标函数 收益
决策变量 单品补货量
约束条件 等式关系
不等式关系(可售单品总数控制、订购量)
问题4 非技术性文章。对于其他的数据寻找,可以制定大方向,在沿用小的方向即可。可以分为宏观、微观;或者动态指标、静态指标。总之一句话,言之有理即可。
相关文章:

2023年高教社杯数学建模国赛 赛题浅析
2023年国赛如期而至,为了方便大家尽快确定选题,这里将对赛题进行浅析,以分析赛题的主要难点、出题思路以及选择之后可能遇到的难点进行说明,方便大家尽快确定选题。 难度排序 B>A>C 选题人数 C>A>B (预估结果&…...
使用QT操作Excel 表格的常用方法
VBA 简介 Microsoft Office软件通常使用VBA来扩展Windows的应用程序功能,Visual Basic for Applications(VBA)是一种Visual Basic的一种宏语言。 在VBA的参考手册中就可以看到具体函数、属性的用法,Qt操作Excel主要通过 QAxObj…...
vue前后端端口不一致解决方案
在config index.js文件中 引入如下代码即可 const path require(path) const devEnv require(./dev.env) module.exports {dev: {// PathsassetsSubDirectory: static,assetsPublicPath: /,proxyTable: devEnv.OPEN_PROXY false ? {} : {/api: {target: http://localhos…...

springcloudSeata处理分布式事务之1.7.0
1.5.0之后版本发生了很大改变 1.seata安装 1.1官网地址 http://seata.io/zh-cn/ 1.2下载地址 https://github.com/seata/seata/releases 下载的是seata-server-1.7.0.zip 1.3seata相关配置的修改 seata-server-1.7.0\seata\conf下的application.yml进行修改 server:por…...

每日刷题|回溯法解决全排列问题
食用指南:本文为作者刷题中认为有必要记录的题目 前置知识:回溯法经典问题之组合 ♈️今日夜电波:爱人错过—告五人 1:11 ━━━━━━️💟──────── 4:52 …...

10-JVM调优工具详解
上一篇:09-JVM垃圾收集底层算法实现 前置启动程序 事先启动一个web应用程序,用jps查看其进程id,接着用各种jdk自带命令优化应用 1.Jmap 此命令可以用来查看内存信息,实例个数以及占用内存大小 jmap -histo 14660 #查看历史…...
)
东方博易oj——3119 - 约瑟夫问题2(链表)
文章目录 题目题目描述输入输出样例输入 输出标签 AC代码 题目 题目描述 约瑟夫问题:有 n n n只猴子,按顺时针方向围成一圈选大王(编号从 1 1 1到 n &#…...
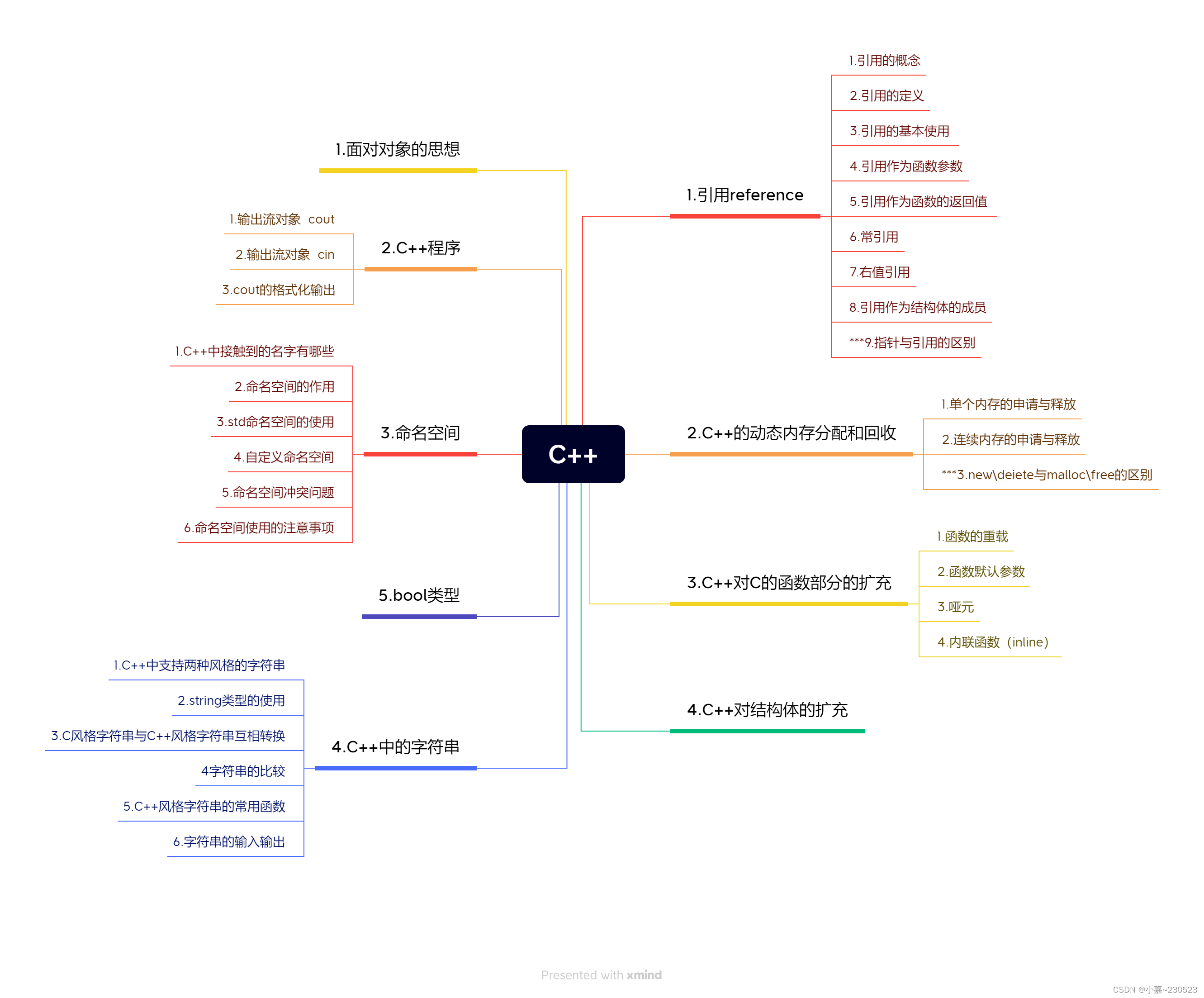
C++,day0907
#include <iostream>using namespace std; struct stu { private:int num; private:double score[32];public:void setNum(){cout <<"请输入学生人数:";cin >>num;}void input(){cout<<"请输入学生的成绩:"<<endl;for(int i…...

孤儿僵尸守护进程的简单理解
孤儿进程: 一个父进程退出,而它的一个或多个子进程还在运行,那么那些子进程将成为孤儿进程。孤儿进程将被init进程所收养,并由init进程对它们完成状态收集工作。 如何模仿一个孤儿进程: 答案是: kill 父…...

学习笔记——Java入门第一季
1.1 Java的介绍与前景 Java语言最早期的制作者:James Gosling(詹姆斯高斯林) 1995年5月23日,Sun Microsystems公司宣布Java语言诞生。 1.2 Java的特性与版本 跨平台 开源(开放源代码) Java代码ÿ…...
更改注册表exe值后的惨痛经历
装软件时由于执行性文件打不开,搜索教程更改了exefile的值,最后整个电脑崩了,所有EXE都打不开,折腾了5个小时,什么办法都试了,甚至重置电脑都不让,打算拿电脑城修电脑了,突然搜到了一…...

stable diffusion实践操作-LyCORIS
系列文章目录 stable diffusion实践操作 文章目录 系列文章目录前言一、LyCORIS是什么?二、使用步骤1.下载2.安装3 使用 二、整理模型1.LoHa-v1.0-pynoise 总结 前言 LyCORIS,可以理解为lora的加强版本。 LyCORIS - Lora beYond Conventional methods,…...
无需公网IP教你如何外网远程访问管家婆ERP进销存
文章目录 前言 1.管家婆服务2. 内网穿透2.1 安装cpolar内网穿透2.2 设置远程访问 3. 固定访问地址4. 配置固定公网访问地址 前言 管家婆辉煌系列产品是中小企业进销存、财务管理一体化的典范软件,历经十余年市场的洗礼,深受广大中小企业的欢迎ÿ…...

Swift使用编解码库Codable
Codable 是 Swift 引入的全新的编解码库,使开发者更方便的解析JSON 或 plist 文件。支持枚举、结构体和类。 Codable协议定义 Codable代表一个同时符合 Decodable 和 Encodable 协议的类型,即可解码且可编码的类型。 typealias Codable Decodable &a…...
Vue + Element UI 前端篇(三):工具模块封装
Vue Element UI 实现权限管理系统 前端篇(三):工具模块封装 封装 axios 模块 封装背景 使用axios发起一个请求是比较简单的事情,但是axios没有进行封装复用,项目越来越大,会引起越来越多的代码冗余&am…...
【pytorch】数据加载dataset和dataloader的使用
1、dataset加载数据集 dataset_tranform torchvision.transforms.Compose([torchvision.transforms.ToTensor(),])train_set torchvision.datasets.CIFAR10(root"./train_dataset",trainTrue,transformdataset_tranform,downloadTrue) test_set torchvision.data…...
搭建单机版FastDFS分布式文件存储系统
一、准备工作 1、下载FastDFS安装包和依赖包 https://codeload.github.com/happyfish100/libfastcommon/tar.gz/V1.0.43 https://codeload.github.com/happyfish100/fastdfs/tar.gz/V6.06 https://codeload.github.com/happyfish100/fastdfs-nginx-module/tar.gz/V1.22 注&…...
【验证码逆向专栏】房某下登录滑块逆向分析
声明 本文章中所有内容仅供学习交流使用,不用于其他任何目的,不提供完整代码,抓包内容、敏感网址、数据接口等均已做脱敏处理,严禁用于商业用途和非法用途,否则由此产生的一切后果均与作者无关! 本文章未…...

Python 3.11 版本是对线程安全做了什么更改吗
问题:这份代码在 3.11.3 中它居然输出 0 ,一度以为自己写错了,抱着不信邪的态度,又搞了个 Python 3.9.7 的环境试了下,果然还是符合自己预期,输出不为 0,想问下 3.11 版本中是做了什么修改吗&am…...
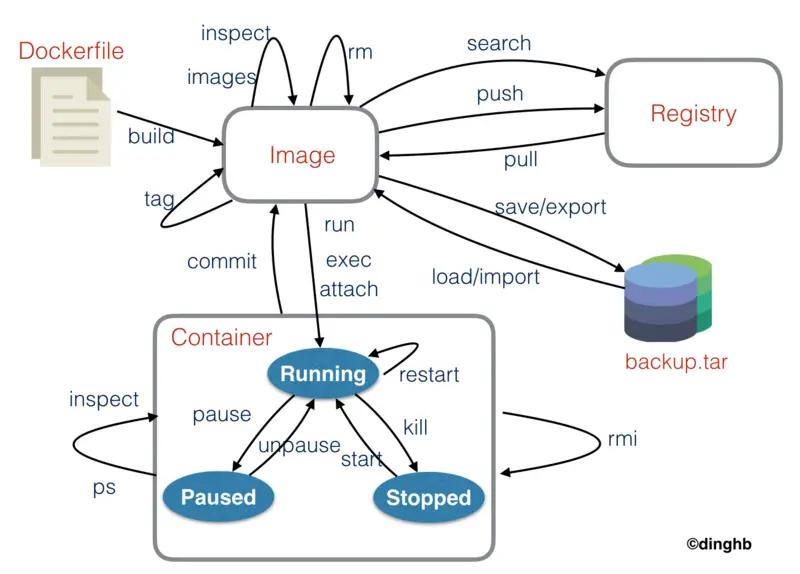
【Docker】镜像的创建、管理与发布
镜像的获取 镜像可以从以下方式获得: 从远程镜像仓库拉取,可以是公有仓库,也可以是私有仓库从Dockerfile构建从文件导入(离线)从容器提交 镜像的基本操作 跟镜像相关的命令如下: $ docker image --help…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
