[BFS] 广度优先搜索
1. 数字操作

常见的模板
// 使用一个数组判断元素是否入过队
int inqueue[N] = {0};// 层数或者可以称为深度
int step = 0;
// 判断是否可以入队的条件
int isvalid(){
}BFS(int x){
// 将初始的元素压入队列
// 注意每次压队的时候都要将inque[x] = 1,表明入队过
queue<int> q;
q.push(x);
inqueue[x] = 1;//大循环 队列q不为空
while (!q.empty()){
// 获得这一层的所有元素 ,因为咱们是广度优先
int cnt = q.size();
//小循环
while (cnt--){
int temp = q.front();
q.pop();
// BFS寻找的目的,这里就是temp 是否 == n
if (temp == n){
return ;//视情况而定
}
// 以此节点开始寻找下一层的有效节点
if (isvalid(temp+1)){
q.push(temp+1);
// 注意压队就要伴随着inqueue[]的变化
inqueue[temp+1] = 1;
}
// ....同理
}
// 在小循环结束后,意味着整层的元素都被遍历过了,若没有,则下一层
step++;
}
}
#include <cstdio>
#include <queue>
using namespace std;
const int N = 1e5+10;
int n;
int inqueue[N] = {0};
int isvalid(int x){if (x<=n && inqueue[x] == 0)return 1;else return 0;
}
int step = 0;
void BFS(){ queue<int> q;q.push(1);inqueue[1] = 1;while (!q.empty()){int cnt = q.size();while (cnt--){int temp = q.front();q.pop();if (temp == n){return;}if (isvalid(temp+1)){q.push(temp+1);inqueue[temp+1] = 1;}if (isvalid(temp*2)){q.push(temp*2);inqueue[temp*2] = 1;}}step++;}
}
int main(){scanf("%d",&n);BFS();printf("%d",step);return 0;
}2. 矩阵的块


题目的思路很简单,首先就是从头到尾遍历数组,当遇到1并且未如过队(证明其是一个全新的块)时进行BFS,直到周围都是0无法进展为止,在BFS过程中,遍历过的1都被压入队中,因此inqueue为1,那么经过几次BFS,证明就有几个块。
#include <cstdio>
#include <queue>
#include <utility>using namespace std;
// 由于需要压队,那么队内的元素为PII
typedef pair<int,int> PII;const int N = 110;
int n,m;
// 是否入队,位置用二维数组即可
int inqueue[N][N] = {0};// 存储整个矩阵
int A[N][N];// 块的数量
int count = 0;// 为了便于上下左右的移动,可以设置两个数组,表示上下左右的变量
int dx[4] = {-1,1,0,0};
int dy[4] = {0,0,-1,1};int isvalid(int x,int y){// 有效的压队条件,x,y未逾越矩阵的范围,未入过队,并且值为1if (x>=1 && x<=n && y>=1 && y<=m && inqueue[x][y] == 0 && A[x][y] == 1)return 1;else return 0;
}
void BFS(int i,int j){queue<PII> q;q.push(make_pair(i,j));inqueue[i][j] = 1;while (!q.empty()){int cnt = q.size();while (cnt--){PII temp = q.front();q.pop();// 我们无需返回什么,因此这里不需要写return 的语句// 开始寻找下一个有效的节点for (int i=0;i<4;i++){int nextx = temp.first+dx[i];int nexty = temp.second+dy[i];if (isvalid(nextx,nexty)){q.push(make_pair(nextx,nexty));inqueue[nextx][nexty] = 1;}}}}
}
int main(){scanf("%d%d",&n,&m);for (int i=1;i<=n;i++)for (int j=1;j<=m;j++)scanf("%d",&A[i][j]);for (int i=1;i<=n;i++)for (int j=1;j<=m;j++)if (A[i][j] == 1 && inqueue[i][j] == 0){BFS(i,j);count++;}printf("%d",count);return 0;
}相关文章:

[BFS] 广度优先搜索
1. 数字操作 常见的模板 // 使用一个数组判断元素是否入过队 int inqueue[N] {0}; // 层数或者可以称为深度 int step 0; // 判断是否可以入队的条件 int isvalid(){ } BFS(int x){ // 将初始的元素压入队列 // 注意每次压队的时候都要将inque[x] 1,表明入队过…...
)
蓝桥杯官网填空题(矩形切割)
题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 小明有一些矩形的材料,他要从这些矩形材料中切割出一些正方形。 当他面对一块矩形材料时,他总是从中间切割一刀,切出一块最大的…...
通过Docker Compose安装MQTT
一、文件和目录说明 1、MQTT安装时的文件和目录 EMQX 安装完成后会创建一些目录用来存放运行文件和配置文件,存储数据以及记录日志。 不同安装方式得到的文件和目录位置有所不同,具体如下: 注意: 压缩包解压安装时,目…...

Golang企业面试题
Golang企业面试题 基础 高级 Golang有哪些优势?Golang数据类型有哪些Golang中的包如何使用Go 支持什么形式的类型转换?什么是 Goroutine?你如何停止它?如何在运行时检查变量类型?Go 两个接口之间可以存在什么关系&a…...
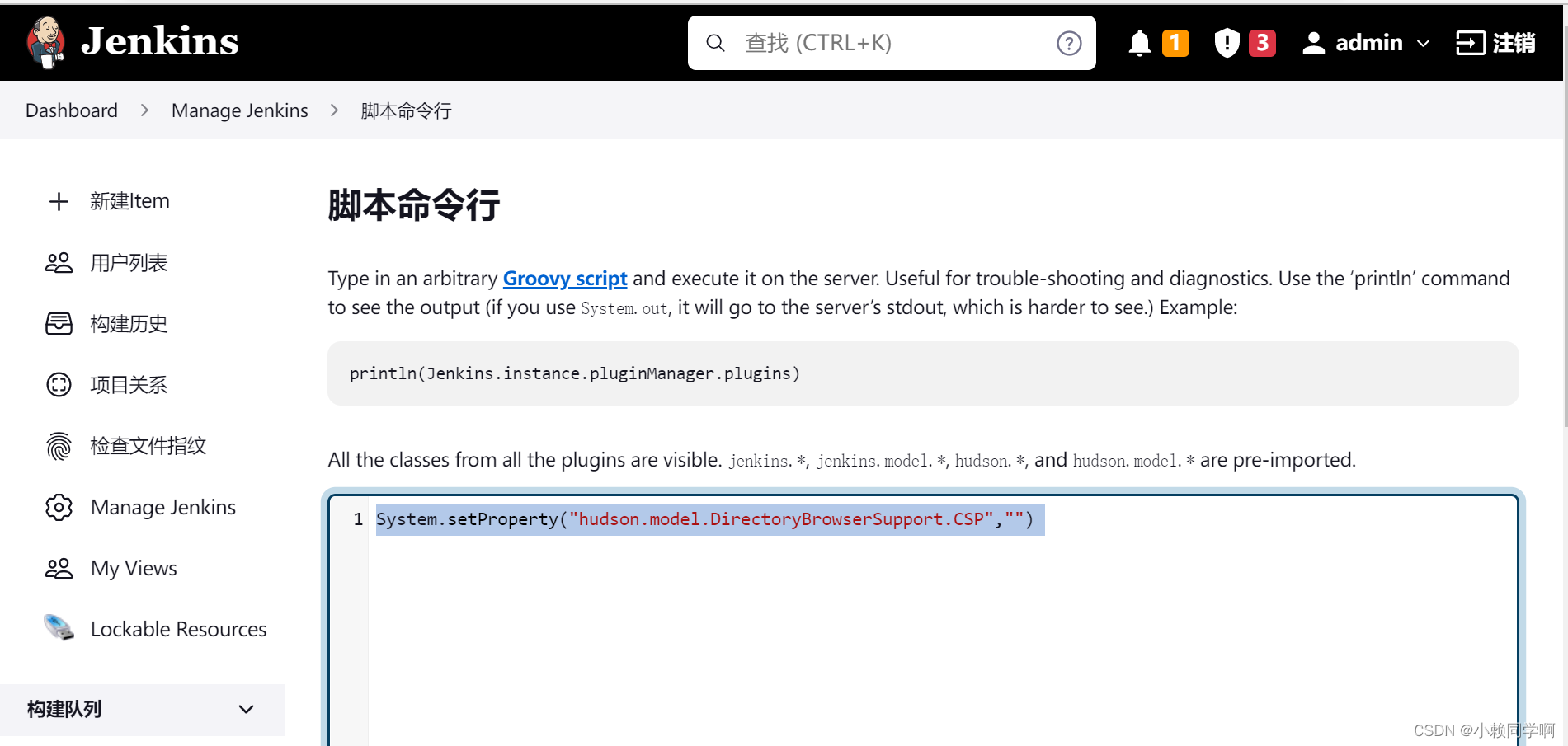
Jenkins测试报告样式优化
方式一:修改Content Security Policy(临时解决,Jenkins重启后失效) 1、jenkins首页—>ManageJenkins—>Tools and Actions标题下—>Script Console 2、粘贴脚本输入框中:System.setProperty("hudson.model.Directo…...
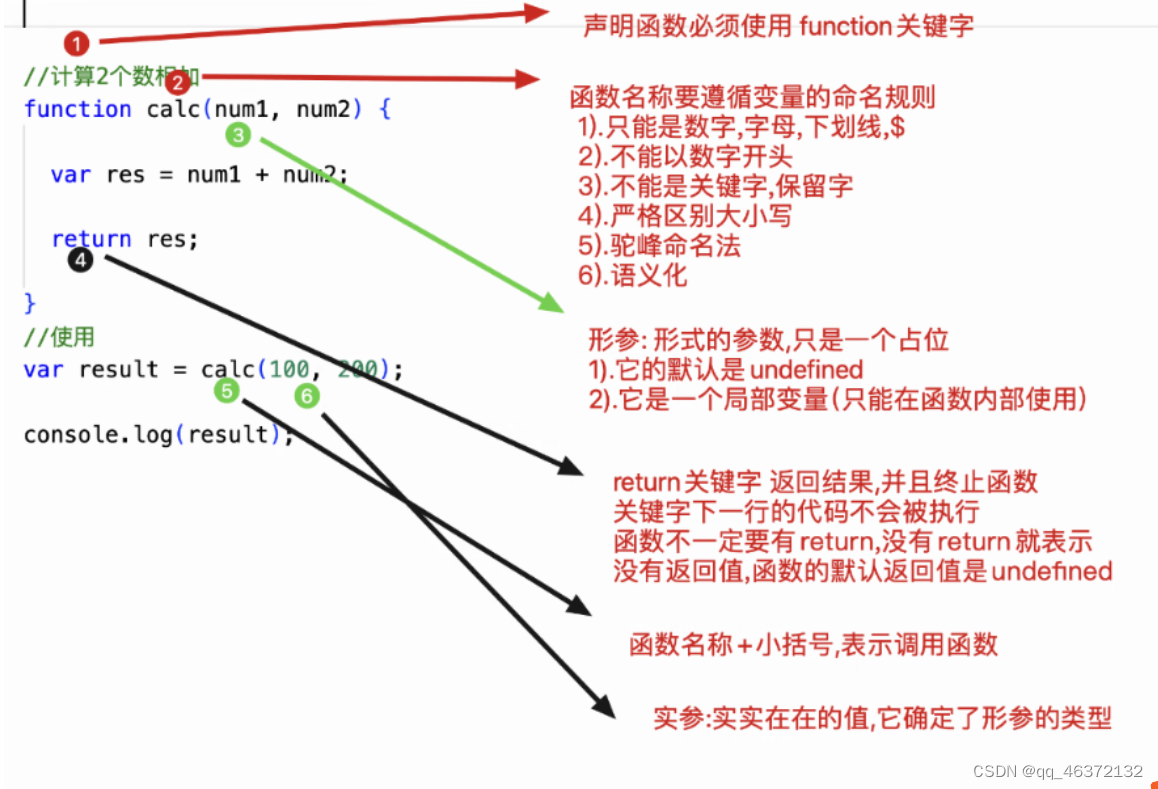
函数相关概念
4.函数 1.函数的概念 1.什么是函数? 把特点的代码片段,抽取成为独立运行的实体 2.使用函数的好处1.重复使用,提供效率2.提高代码的可读性3.有利用程序的维护 3.函数的分类1.内置函数(系统函数)已经提高的alert(); prompt();confirm();print()document.write(),console.log()…...

2023软考学习营
...
Vue2进阶篇学习笔记
文章目录 Vue2进阶学习笔记前言1、Vue脚手架学习1.1 Vue脚手架概述1.2 Vue脚手架安装1.3 常用属性1.4 插件 2、组件基本概述3、非单文件组件3.1 非单文件组件的基本使用3.2 组件的嵌套 4、单文件组件4.1 快速体验4.2 Todo案例 5、浏览器本地存储6、组件的自定义事件6.1 使用自定…...

Python 正则表达式:强大的文本处理工具
概念: 正则表达式是一种强大的文本匹配和处理工具,它可以用来在字符串中查找、替换和提取符合某种规则的内容。在Python中,使用re模块可以轻松地操作正则表达式,它提供了丰富的功能和灵活的语法。 场景: 正则表达式…...

Linux如何查看系统时间
文章目录 一、使用date命令查看系统时间二、通过/var/log/syslog文件查看系统时间三、通过/proc/uptime文件查看系统运行时间四、通过hwclock命令查看硬件时间五、通过timedatectl命令设置系统时区六、通过NTP协议同步网络时间七、通过ntpstat命令检查NTP同步状态八、使用cal命…...

46. 出勤率问题
文章目录 题目需求实现一题目来源 题目需求 现有用户出勤表(user_login)如下。 user_id (用户id)course_id (课程id)login_in (登录时间)login_out (登出时间)112022-06-02 09:08:242022-06-02 10:09:361…...
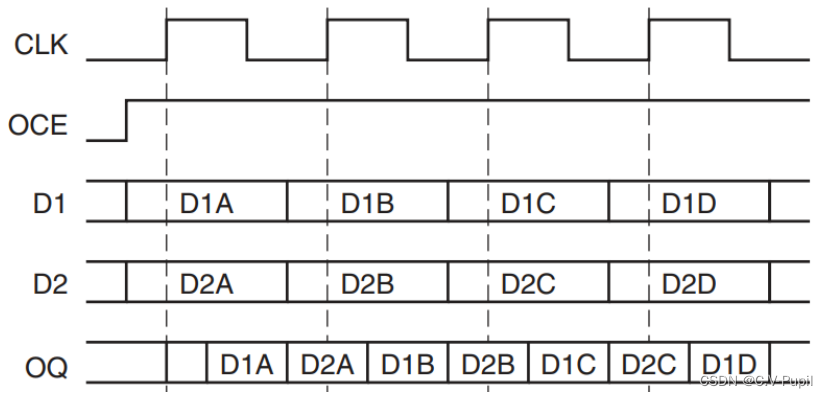
Xilinx IDDR与ODDR原语的使用
文章目录 ODDR原语1. OPPOSITE_EDGE 模式2. SAME_EDGE 模式 ODDR原语 例化模板: ODDR #(.DDR_CLK_EDGE("OPPOSITE_EDGE"), // "OPPOSITE_EDGE" or "SAME_EDGE" .INIT(1b0), // Initial value of Q: 1b0 or 1b1.SRTYPE("SYNC…...

面试系列 - 序列化和反序列化详解
Java 序列化是一种将对象转换为字节流的过程,可以将对象的状态保存到磁盘文件或通过网络传输。反序列化则是将字节流重新转换为对象的过程。Java 提供了一个强大的序列化框架,允许你在对象的持久化和网络通信中使用它。 一、Java 序列化的基本原理 Jav…...
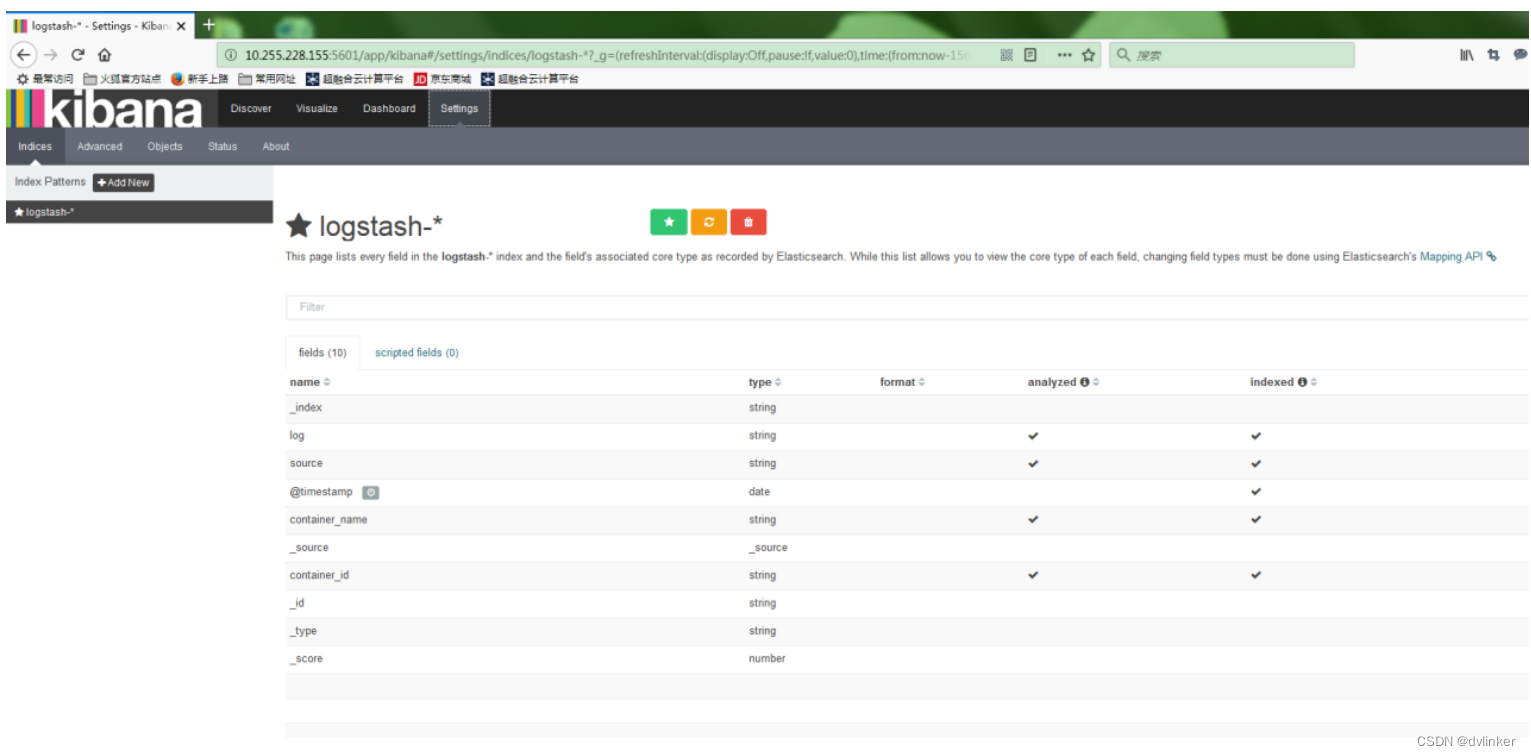
基于Elasticsearch + Fluentd + Kibana(EFK)搭建日志收集管理系统
目录 1、EFK简介 2、EFK框架 2.1、Fluentd系统架构 2.2、Elasticsearch系统架构 2.3、Kibana系统架构 3、Elasticsearch接口 4、EFK在虚拟机中安装步骤 4.1、安装elasticsearch 4.2、安装kibana 4.3、安装fluentd 4.4、进入kibana创建索引 5、Fluentd配置介绍 VC常…...

【Python小项目之Tkinter应用】解决Python的Pyinstaller将.py文件打包成.exe可执行文件后文件过大的问题
文章目录 前言1. 创建新项目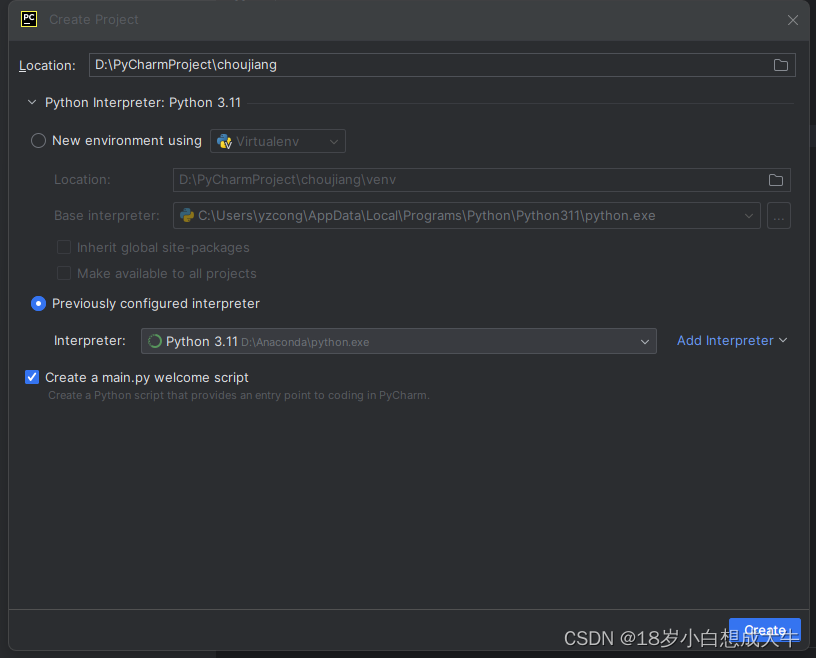2.删除原项目中的全部文件3.将要打包的文件放入该项目目录下4.创建虚拟环境5.设置解释器为虚拟环境中的python解释器6.查看是否成功使用虚拟环境中的python解…...

Ab3d.DXEngine 6.0 Crack 2023
Ab3d.DXEngine 不是另一个游戏引擎(如Unity),它强迫您使用其游戏编辑器、其架构,并且需要许多技巧和窍门才能在标准 .Net 应用程序中使用。Ab3d.DXEngine 是一个新的渲染引擎,它是从头开始构建的,旨在用于标…...

Wireshark抓包常用指令
1.常用过滤规则 指定源地址: ip.src 10.0.1.123ip.src 10.0.1.123 && udphttp数据链路层:筛选mac地址为04:f9:38:ad:13:26的数据包----eth.src 04:f9:38:ad:13:26筛选源mac地址为04:f9:38:ad:13:26的数据包----eth.src 04:f9:38:ad:13:26网…...
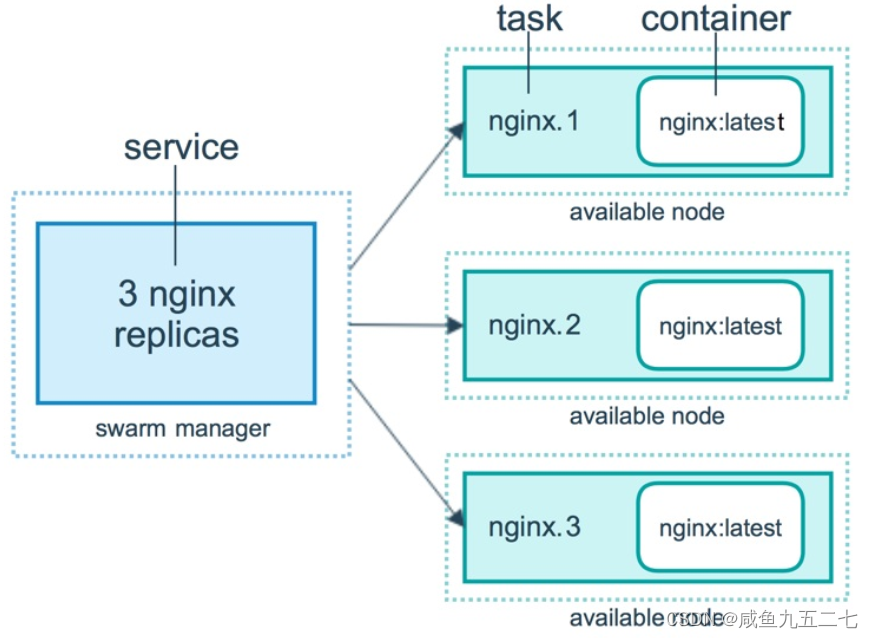
Docker Swarm
Docker Swarm提供 Docker 容器集群服务,是 Docker 官方对容器云生态进行支持的核心方案。将多个 Docker 主机封装为单个大型的虚拟 Docker 主机,快速打造一套容器云平台。 Swarm mode内置 kv 存储功能,提供了众多的新特性,比如&a…...

jupyter notebook安装和删除kernel的解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...

中级深入--day16
爬虫(Spider),反爬虫(Anti-Spider),反反爬虫(Anti-Anti-Spider) 之间恢宏壮阔的斗争... Day 1 小黄想要某站上所有的电影,写了标准的爬虫(基于HttpClient库),不断地遍历某站的电影列表页面,根据 Html 分析电影名字存进…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
