美的的笔试
第一题
有两只猫咪和n条不同类型的鱼,每条鱼都只能被其中一只猫咪吃掉。
下标为i处的鱼被吃掉的得分为:
如果第一只猫咪吃掉,则得分为reward1[i]。如果第二只猫咪吃掉,则得分为reward[i]。
给你一个正整数数组reward1 ,一个正整数数组reward2,和一个非负整数k。
请你返回第一只猫咪恰好吃掉k条鱼的情况下,最大得分为多少。
输入
1 1 3 4
4 4 1 1
2
输出
15
说明
这个例子中,第一只猫咪吃掉第2和3条鱼(下标从0于始),第二只猫咪吃掉第0和1条鱼。
总得分为4+4+3+4=15。
15是最高得分。
思路
- 定义状态:令 dp[i][j] 表示第一只猫咪吃掉 i 条鱼,第二只猫咪吃掉 j 条鱼时,能得到的最大得分。
- 初始状态:dp[0][0] = 0,表示两只猫咪都没有吃鱼时,得分为 0。
- 状态转移:对于每一条鱼,有三种选择:
- 第一只猫咪吃掉,那么 dp[i][j] = dp[i-1][j] + reward1[i+j-1],其中 reward1[i+j-1] 表示第 i+j-1 条鱼的得分。
- 第二只猫咪吃掉,那么 dp[i][j] = dp[i][j-1] + reward2[i+j-1],其中 reward2[i+j-1] 表示第 i+j-1 条鱼的得分。
- 两只猫咪都不吃,那么 dp[i][j] = dp[i][j],不改变得分。
- 取这三种选择中的最大值作为 dp[i][j] 的值。
- 最终答案:由于题目要求第一只猫咪恰好吃掉 k 条鱼,那么最终答案就是 dp[k][n-k],其中 n 是鱼的总数。
#include <iostream>
#include <vector>
using namespace std;int maxScore(vector<int>& reward1, vector<int>& reward2, int k) {int n = reward1.size(); // 鱼的总数vector<vector<int>> dp(k + 1, vector<int>(n - k + 1, 0)); // 定义状态数组for (int i = 0; i <= k; i++) { // 遍历第一只猫咪吃掉的鱼数for (int j = 0; j <= n - k; j++) { // 遍历第二只猫咪吃掉的鱼数if (i == 0 && j == 0) continue; // 跳过初始状态int score = 0; // 记录当前得分if (i > 0) { // 如果第一只猫咪可以吃掉一条鱼score = max(score, dp[i-1][j] + reward1[i+j-1]); // 更新得分}if (j > 0) { // 如果第二只猫咪可以吃掉一条鱼score = max(score, dp[i][j-1] + reward2[i+j-1]); // 更新得分}dp[i][j] = score; // 更新状态数组}}return dp[k][n-k]; // 返回最终答案
}int main() {vector<int> reward1 = {1, 1, 3, 4}; // 输入第一只猫咪的得分数组vector<int> reward2 = {4, 4, 1, 1}; // 输入第二只猫咪的得分数组int k = 2; // 输入第一只猫咪要吃掉的鱼数cout << maxScore(reward1, reward2, k) << endl; // 输出最大得分return 0;
}
第二题
在一个城市探险活动中,主办方标记了n个地标,编号为0到n-1。大壮需要从城市的起点(编号为0的地标)经过一系列地标后,最终到达终点(编号为n-1的地标)。每个地标都对应一个整数,表示从当前地标可以跳过的地标数量。例如,如果小王当前处于编号为i的地标,且地标对于的数字为nums[i],那么他可以选择跳过中间所有地标,而是直接去往任意编号为i用j的地标,其中0<=j= nums[i]且i+j<n。主办方确保有路线可以成功到达终点地标,为了顺利到达终点,请帮助大壮计算,他需要经过的最少的地标数量。
输入描述:
地标组数
输出描述:
经过最少地标数量
示例1
输入
[2, 1, 1,3, 1, 3, 1, 4]
输出
4
示例2
输入
[5, 4, 3, 2, 1,2, 3, 1, 1, 2]
输出
3
思路:
- 定义一个变量 ans 表示经过的地标数量,初始为 0。
- 定义一个变量 cur 表示当前所在的地标编号,初始为 0。
- 定义一个变量 next 表示下一步要跳到的地标编号,初始为 0。
- 使用一个 while 循环,当 cur < n - 1 时,执行以下操作:
- 遍历从 cur + 1 到 cur + nums[cur] 的所有地标编号 i,找出使得 i + nums[i] 最大的那个 i,并赋值给 next。
- 如果 next == cur,说明无法继续前进,返回 -1 表示无解。
- 否则,将 cur 更新为 next,并将 ans 加一。
- 返回 ans 作为最终答案。
根据以上思路,可以用 C++ 语言编写如下代码:
#include <iostream>
#include <vector>
using namespace std;int minLandmarks(vector<int>& nums) {int n = nums.size(); // 地标的总数int ans = 0; // 经过的地标数量int cur = 0; // 当前所在的地标编号int next = 0; // 下一步要跳到的地标编号while (cur < n - 1) { // 当没有到达终点时int max_jump = 0; // 记录能跳到的最远距离for (int i = cur + 1; i <= cur + nums[cur]; i++) { // 遍历所有可选的地标if (i + nums[i] > max_jump) { // 如果能跳得更远max_jump = i + nums[i]; // 更新最远距离next = i; // 更新下一步目标}}if (next == cur) return -1; // 如果无法前进,返回-1表示无解cur = next; // 更新当前位置ans++; // 更新经过的地标数量}return ans; // 返回最终答案
}int main() {vector<int> nums = {2, 1, 1, 3, 1, 3, 1, 4}; // 输入地标组数cout << minLandmarks(nums) << endl; // 输出经过最少地标数量return 0;
}
相关文章:

美的的笔试
第一题 有两只猫咪和n条不同类型的鱼,每条鱼都只能被其中一只猫咪吃掉。 下标为i处的鱼被吃掉的得分为: 如果第一只猫咪吃掉,则得分为reward1[i]。如果第二只猫咪吃掉,则得分为reward[i]。 给你一个正整数数组reward1 ,一个正整数数组reward2࿰…...

Android 1.2 开发环境搭建
目录 1.2 开发环境搭建 1.JDK安装与配置 2.开发工具二选一 3.相关术语的解析 4.ADB命令行的一些指令 5.APP程序打包与安装的流程: 6.APP的安装过程: 7.本节小结 1.2 开发环境搭建 现在主流的Android开发环境有: ①Eclipse ADT SDK ②Android Stu…...
vue 页面加水印
首先创建一个waterMark.js文件,当然文件命名可自定义, use strictconst watermark {}/**** param {要设置的水印的内容} str* param {需要设置水印的容器} container*/ const setWatermark (str, container) > {const id 1.23452384164.123412415…...

Android ImageView详解
scaleType属性详解 在 Android 中,ImageView 控件的 scaleType 属性用于指定图像在 ImageView 内部的缩放和对齐方式。scaleType 属性可以帮助你控制图像的显示方式,以适应 ImageView 的尺寸或实现其他特定的显示效果。以下是常见的 scaleType 属性值和…...
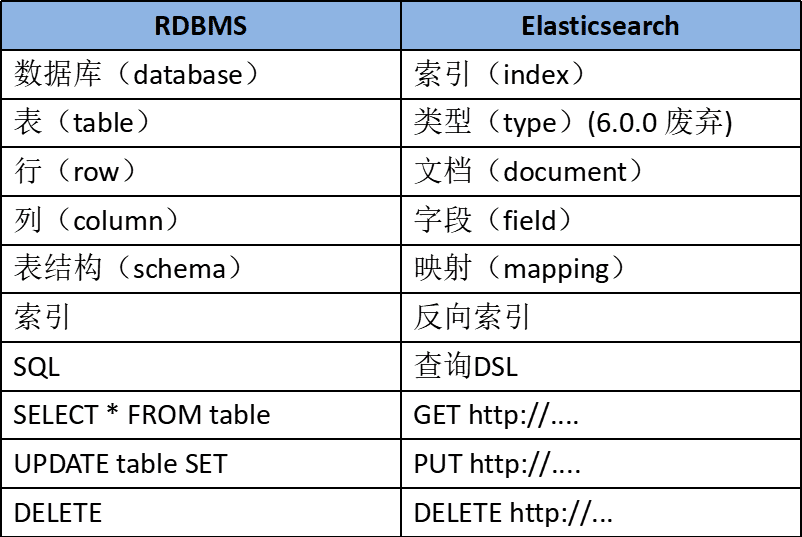
ElasticSearch第二讲:ES详解 - ElasticSearch基础概念
ElasticSearch第二讲:ES详解 - ElasticSearch基础概念 在学习ElasticSearch之前,先简单了解下ES流行度,使用背景,以及相关概念等。本文是ElasticSearch第二讲,ElasticSearch的基础概念。 文章目录 ElasticSearch第二讲…...

Ajax模拟视频点赞功能
前台 <%--Created by IntelliJ IDEA.User: xxDate: 2023/9/4Time: 10:00To change this template use File | Settings | File Templates. --%> <% page contentType"text/html;charsetUTF-8" language"java" %> <html> <head>&l…...

java解决 衣服尺码 Compare T-Shirt Sizes
java解决衣服尺码 时间限制:3000MS 内存限制:589824KB 题目描述: 一般来说衣服尺码分为L,M,S三种,分别代表大(Large),中(Medium)和小(Small)。不过由于人的身高差异性较大,尺码又会…...

基于python+Django深度学习的音乐推荐方法研究系统设计与实现
摘 要 数字化时代带动着整个社会的信息化发展,随着数字媒体的不断发展,现在通多媒体数字产品的内容越来越丰富,传播影响力越来越强,以音乐为例,现在的音乐文化多样、音乐资源也异常的丰富,在这种大数据的环…...

【枚举区间+线段树】CF Ehu 152 E
Problem - E - Codeforces 题意: 思路: 感觉是个套路题 对区间计数,按照CF惯用套路,枚举其中一个端点,对另一个端点计数 对于这道题,枚举右端点,对左端点计数 Code: #include &…...

宏定义天坑记录
宏定义天坑记录 事件原委与推理过程 在编译一个使用了Protobuf的项目时出现了如下报错 [ybVM-8-7-centos boost_searcher]$ make g -o http_server http_server.cc data/raw_html.pb.cc -stdc11 -lboost_system -lboost_filesystem -lpthread -ljsoncpp -lprotobuf In file…...

Git的一些常用概念与操作方法分享
Git是一个版本控制系统,它可以记录代码的变化历史并允许多个开发者同时对同一代码库进行开发。以下是Git的基本概念和使用方式: 仓库(Repository)- 保存代码的地方。Git仓库包含了所有的版本历史记录、代码以及其他相关文件。 分…...

webpack实战:某网站JS逆向分析
文章目录 1. 写在前面2. 抓包分析3. 扣加密代码 1. 写在前面 好的逆向能够帮助我们了解加密实现,然后根据加密方式(md5,base64,res,des,rsa…)还原加密算法的过程。可以看看我之前的这篇文章:快速定位查找加密方式特征与技巧 目标站点&#…...

826. 安排工作以达到最大收益;2257. 统计网格图中没有被保卫的格子数;816. 模糊坐标
826. 安排工作以达到最大收益 核心思想:排序维护最大利润。首先我们需要对工人按照能力排序,前面工人满足的最大利润后面的工人肯定是满足的,所以我们只需要用一个tmp来维护小于等于当前工人的最大利润,然后如何得到tmpÿ…...

JAVA毕业设计097—基于Java+Springboot+Vue+uniapp的医院挂号小程序系统(源码+数据库)
基于JavaSpringbootVueuniapp的医院挂号小程序系统(源码数据库)097 一、系统介绍 本系统前后端分离(网页端和小程序端都有) 本系统分为管理员、医院、用户三种角色(角色菜单可自行分配) 用户功能: 注册、登录、医院搜索、最新资讯、医生搜索、挂号预约、挂号记…...
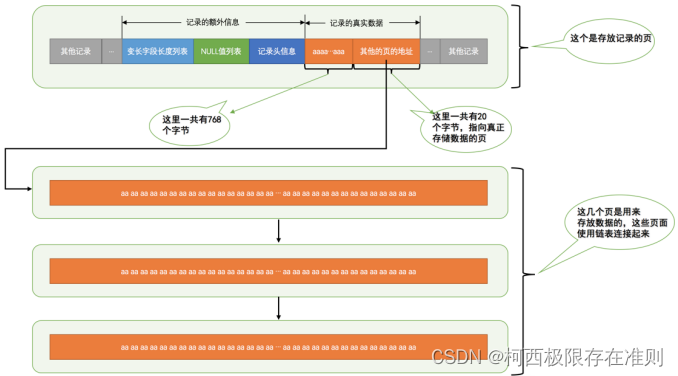
4.3.3.1 【MySQL】CHAR(M)列的存储格式
我们知道 Compact 行格式在 CHAR(M) 类型的列中存储数据的时候还挺麻烦,分变长字符集和定长字符集的情况,而在 Redundant 行格式中十分干脆,不管该列使用的字符集是啥,只要是使用 CHAR(M) 类型,占用的真实数据空间就是…...

js 处理数组合并vs对象合并
前言: 前端开发中,我们会遇到各种数据的需求,但是后端给你返回的数据结构又不是你想要的, 只能自己动手,去组装数据,重新定义数据结构了。 1. js 数组合并的方法 常用的应该是 concat 方法. 示例: let arr1 […...

Webpack vs Vite的核心差异
构建速度: Webpack: Webpack的构建速度相对较慢,尤其在大型项目中,因为它需要分析整个依赖图,进行多次文件扫描和转译。Vite: Vite以开发模式下的极速构建著称。它利用ES模块的特性,只构建正在编辑的文件,而不是整个项…...
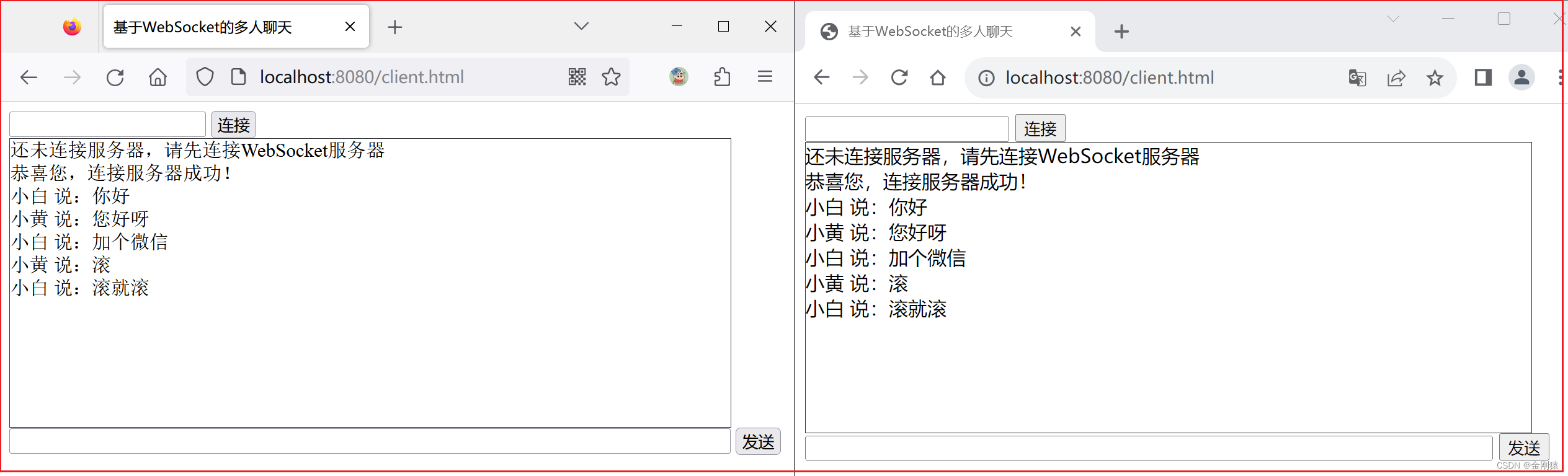
53、springboot对websocket的支持有两种方式-------1、基于注解开发 WebSocket ,简洁实现多人聊天界面
基于注解开发 WebSocket –注解就是: OnOpen、 OnClose 、 OnMessage 、OnError这些 ★ WebSocket的两种开发方式 ▲ Spring Boot为WebSocket提供了两种开发方式: 基于spring-boot-starter-websocket.jar开发WebSocket 基于Spring WebFlux开发WebSoc…...

18 Linux之Python定制篇-Python开发平台Ubuntu
18 Linux之Python定制篇-Python开发平台Ubuntu 文章目录 18 Linux之Python定制篇-Python开发平台Ubuntu18.1 安装Ubuntu虚拟机18.4 Ubuntu的root用户18.5 Ubuntu下开发Python 学习视频来自于B站【小白入门 通俗易懂】2021韩顺平 一周学会Linux。可能会用到的资料有如下所示&…...

AMEYA360:士兰微推出600A/1200V IGBT汽车驱动模块,提升充电速度与行驶动力
随着人们对环保意识的提高和汽车驾驶体验感的不断追求,新能源汽车的市场需求逐渐增大,已然成为汽车发展的大趋势,但是新能源汽车充电时间长、续航里程短等问题仍然是汽车厂商和车主们的痛点。因此,需要更好的汽车驱动产品来实现“…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
