T检验的前提条件|独立性|方差齐性|随机抽样
T检验是一种用于比较两组数据均值是否存在显著差异的统计方法,但在进行T检验之前,有一些前提条件需要满足,以确保结果的准确性和可靠性。这些前提条件包括:
-
正态性:T检验要求数据在每个组内都服从正态分布。正态性可以使用统计方法(如正态分布检验)或图形方法(如Q-Q图)来进行检验。如果数据不服从正态分布,可以考虑进行数据变换或使用非参数检验方法。
-
独立性:观测值必须相互独立。这意味着一个组内的观测值不应受到另一个组内的观测值影响,例如,不应存在重复测量或相关性。
-
方差齐性:T检验假设两组数据的方差相等(方差齐性)。可以使用统计方法(如方差齐性检验)来检验两组数据的方差是否相等。如果方差不齐性显著,可以考虑使用修正的T检验方法(如Welch's T检验)。
-
随机抽样:数据必须是随机抽样得到的,以确保结果具有代表性,并且可以推广到总体。
如果数据不符合这些前提条件,可能会影响T检验结果的准确性。在某些情况下,可以尝试使用非参数检验方法,如Wilcoxon秩和检验,来处理不满足前提条件的数据。
在进行T检验之前,建议进行数据探索和统计检验,以确定是否满足这些前提条件,并采取适当的措施来处理不满足条件的情况。这样可以确保T检验结果的可靠性和有效性。
当涉及到T检验的前提条件时,让我们通过一个具体的例子来详细说明每个前提条件,并使用Python来实现相应的检验和处理。
问题1:正态性
正态性是T检验的一个重要前提条件。我们首先需要检验两个组的数据是否符合正态分布。我们可以使用Shapiro-Wilk正态性检验来进行检验。假设我们有两组成绩数据,分别是A组和B组,我们想要比较它们是否存在显著差异。
import scipy.stats as stats
import numpy as np# 生成示例数据
np.random.seed(0)
group_A = np.random.normal(0, 1, 50)
group_B = np.random.normal(0.5, 1, 50)# 正态性检验
statistic_A, p_value_A = stats.shapiro(group_A)
statistic_B, p_value_B = stats.shapiro(group_B)print("Group A 正态性检验结果:Statistic =", statistic_A, ", p-value =", p_value_A)
print("Group B 正态性检验结果:Statistic =", statistic_B, ", p-value =", p_value_B)
如果p-value小于显著性水平(通常为0.05),则我们可以拒绝原假设,表示数据不服从正态分布。在这种情况下,我们可能需要考虑使用非参数检验方法或尝试对数据进行变换。
问题2:独立性
独立性是T检验的另一个前提条件。确保两组数据之间没有相关性或干扰因素是很重要的。例如,我们想要比较两个不同课堂上学生的考试成绩,确保每个学生仅出现在一个组中。
问题3:方差齐性
方差齐性是T检验的前提条件之一。我们可以使用Levene's方差齐性检验来检验两组数据的方差是否相等。假设我们有两组不同药物治疗的患者的生命持续时间数据,我们想要比较它们是否存在显著差异。
# 生成示例数据
np.random.seed(1)
group_1 = np.random.normal(5, 2, 50)
group_2 = np.random.normal(5, 4, 50)# 方差齐性检验
statistic, p_value = stats.levene(group_1, group_2)print("方差齐性检验结果:Statistic =", statistic, ", p-value =", p_value)
如果p-value小于显著性水平,我们可以拒绝方差齐性假设,表明两组数据的方差不相等。在这种情况下,我们可以考虑使用Welch's T检验等不要求方差相等的T检验方法。
问题4:随机抽样
确保数据是随机抽样得到的是一个基本前提条件,以确保结果具有代表性。随机抽样意味着每个个体有相等的机会被选入样本中,而不受其他因素的干扰。
总之,这些前提条件对于T检验的准确性至关重要。在实际应用中,您应该根据数据的特点来检验和满足这些前提条件,以确保您的T检验结果可靠。如果不满足这些条件,可以考虑使用适当的替代方法或数据处理技巧。
Shapiro-Wilk正态性检验是一种用于检验数据是否来自正态分布的统计方法。该检验的原假设是数据样本服从正态分布。如果p-value小于显著性水平(通常为0.05),则我们可以拒绝原假设,表明数据不服从正态分布。
以下是Python中使用Shapiro-Wilk正态性检验的示例代码:
import scipy.stats as stats
import numpy as np# 生成示例数据
np.random.seed(0)
data = np.random.normal(0, 1, 100)# 进行Shapiro-Wilk正态性检验
statistic, p_value = stats.shapiro(data)# 输出检验结果
print("Shapiro-Wilk正态性检验结果:Statistic =", statistic, ", p-value =", p_value)# 根据p-value判断正态性
alpha = 0.05
if p_value > alpha:print("样本数据可能来自正态分布(无法拒绝正态性假设)")
else:print("样本数据不来自正态分布(拒绝正态性假设)")
在这个示例中,我们生成了一个服从正态分布的随机数据样本,然后使用Shapiro-Wilk检验来检验它是否符合正态分布。根据p-value的结果,我们可以判断数据是否来自正态分布。
请注意,Shapiro-Wilk检验对于大样本通常会有较高的功效,但对于小样本也可以使用。如果p-value小于显著性水平,表明数据不服从正态分布,您可能需要考虑使用非参数统计方法或对数据进行适当的转换。
相关文章:

T检验的前提条件|独立性|方差齐性|随机抽样
T检验是一种用于比较两组数据均值是否存在显著差异的统计方法,但在进行T检验之前,有一些前提条件需要满足,以确保结果的准确性和可靠性。这些前提条件包括: 正态性:T检验要求数据在每个组内都服从正态分布。正态性可以…...
【GO语言基础】变量常量
系列文章目录 【Go语言学习】ide安装与配置 【GO语言基础】前言 【GO语言基础】变量常量 【GO语言基础】数据类型 【GO语言基础】运算符 文章目录 系列文章目录常量和枚举变量声明全局变量声明大小写敏感 总结 常量和枚举 使用const关键字声明常量,并为每个常量提…...

C++QT day3
1> 自行封装一个栈的类,包含私有成员属性:栈的数组、记录栈顶的变量 成员函数完成:构造函数、析构函数、拷贝构造函数、入栈、出栈、清空栈、判空、判满、获取栈顶元素、求栈的大小 2> 自行封装一个循环顺序队列的类,包含…...
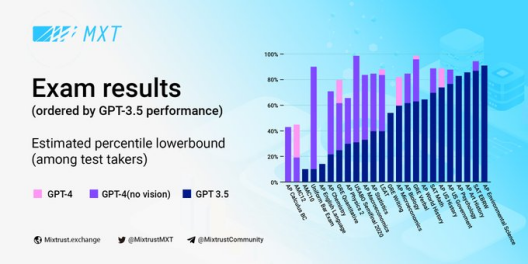
AI时代的较量,MixTrust能否略胜一筹?
人工智能的能力正在迅速接近人类,而在许多细分领域,已经超越了人类。虽然短期内这个突破是否会导致人工通用智能(AGI)还不清楚,但我们现在有的模型被训练成在数字交互中完美地模仿高能人类。尽管AGI仍不确定࿰…...
Ubuntu22.04 安装 MongoDB 7.0
稍微查了一些文章发现普遍比较过时。有的是使用旧版本的Ubuntu,或者安装的旧版本的MongoDB。英语可以的朋友可以移步Install MongoDB Community Edition on Ubuntu — MongoDB Manual,按照官方安装文档操作。伸手党或者英语略差的朋友可以按照本文一步步…...

【日志技术——Logback日志框架】
日志技术 1.引出 我们通常展示信息使用的是输出语句,但它有弊端,只能在控制台展示信息,不能灵活的指定日志输出的位置(文件,数据库),想加入或取消日志,需要修改源代码 2.日志技术…...

mysql存储过程和函数
存储过程语法 设置变量: set dogNum 1002; 1、无参的存储过程 delimiter $ CREATE PROCEDURE 存储过程名() begin 存储过程体 end $; 2、有参数的存储过程 delimiter $ CREATE PROCEDURE 存储过程名(in|out|inout 参数名1 参数类型,参数名2 参数类型……...

【HDFS】Hadoop-RPC:客户端侧通过Client.Connection#sendRpcRequest方法发送RPC序列化数据
org.apache.hadoop.ipc.Client.Connection#sendRpcRequest: 这个方法是客户端侧向服务端发送RPC请求的地方。调用点是Client#call方法过来的。 此方法代码注释里描述了一个细节:这个向服务端发送RPC请求数据的过程并不是由Connection线程发送的,而是其他的线程(sendParams…...
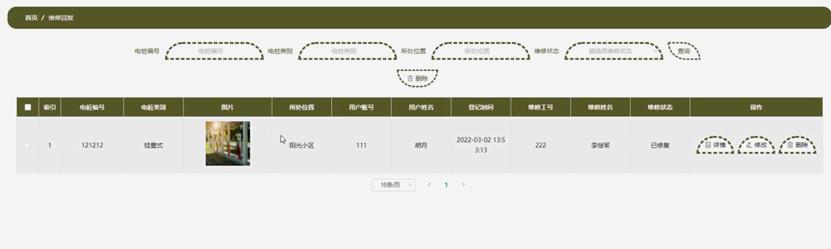
Java基于 SpringBoot 的车辆充电桩系统
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W,Csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 文章目录 1、效果演示效果图技术栈 2、 前言介绍(完整源码请私聊)3、主要技术3.4.1 …...

excel表导出
dto:查询条件所在的类 GetMapping(value "/downloadProject")ApiOperation("导出台账数据")AnonymousAccesspublic void queryDownload(Dto dto, HttpServletResponse response) throws IOException, ParseException {service.queryDownload(byPageDto, re…...

YOLOv8 快速入门
前言 本文是 YOLOv8 入门指南(大佬请绕过),将会详细讲解安装,配置,训练,验证,预测等过程 YOLOv8 官网:ultralytics/ultralytics: NEW - YOLOv8 🚀 in PyTorch > ONN…...

HJ48 从单向链表中删除指定值的节点
Powered by:NEFU AB-IN Link 文章目录 HJ48 从单向链表中删除指定值的节点题意思路代码 HJ48 从单向链表中删除指定值的节点 题意 输入一个单向链表和一个节点的值,从单向链表中删除等于该值的节点,删除后如果链表中无节点则返回空指针。 思路 单向链表…...

Java缓存理解
CPU占用:如果你有某些应用需要消耗大量的cpu去计算,比如正则表达式,如果你使用正则表达式比较频繁,而其又占用了很多CPU的话,那你就应该使用缓存将正则表达式的结果给缓存下来。 数据库IO性能:如果发现有大…...

MHA高可用及故障切换
一、什么是 MHA MHA(MasterHigh Availability)是一套优秀的MySQL高可用环境下故障切换和主从复制的软件。 MHA 的出现就是解决MySQL 单点的问题。 MySQL故障切换过程中,MHA能做到0-30秒内自动完成故障切换操作。 MHA能在故障切换的过程中最大…...

1000元订金?华为折叠屏手机MateX5今日开始预订,售价尚未公布
华为最新款折叠屏手机Mate X5今日在华为商城开始预订,吸引了众多消费者的关注。预订时需交纳1000元的订金,而具体售价尚未公布。据华为商城配置表显示,Mate X5预计将搭载Mate 60系列同款麒麟9000S处理器,或可能搭载麒麟9100处理器…...
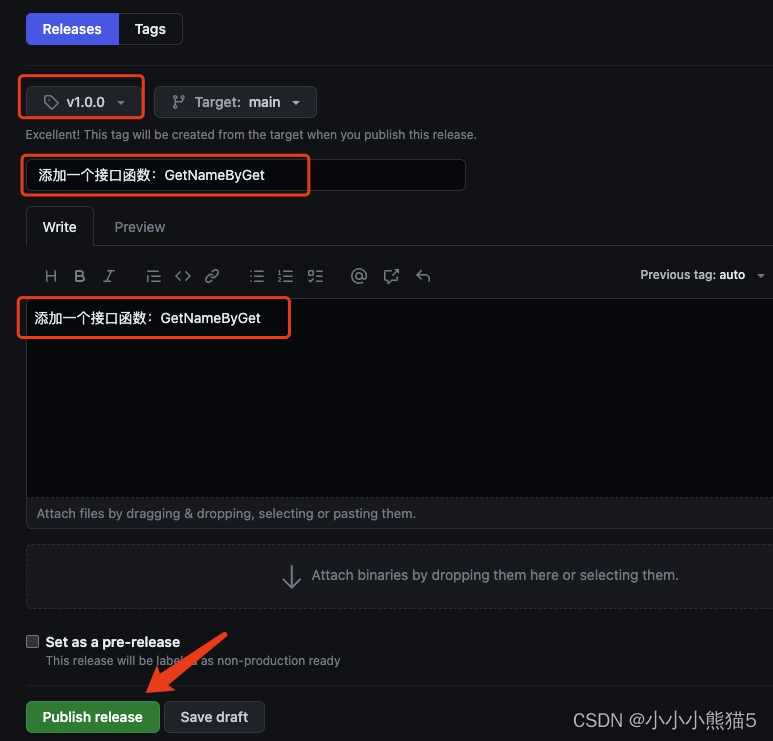
Golang编写客户端SDK,并开源发布包到GitHub,供其他项目import使用
目录 编写客户端SDK,并开源发布包到GitHub1. 创建 GitHub 仓库2. 构建项目,编写代码Go 代码示例:项目目录结构展示: 3. 提交代码到 GitHub仓库4. 发布版本5. 现在其他人可以引用使用你的模块包了 编写客户端SDK,并开源…...

手写Mybatis:第10章-使用策略模式,调用参数处理器
文章目录 一、目标:参数处理器二、设计:参数处理器三、实现:参数处理器3.1 工程结构3.2 参数处理器关系图3.3 入参数校准3.4 参数策略处理器3.4.1 JDBC枚举类型修改3.4.2 类型处理器接口3.4.3 模板模式:类型处理器抽象基类3.4.4 类…...

pair 是 C++ 标准库中的一个模板类,用于存储两个对象的组合
pair 是 C 标准库中的一个模板类,用于存储两个对象的组合。它位于 <utility> 头文件中。 pair 类的定义如下: template <class T1, class T2> struct pair {T1 first;T2 second;pair();pair(const T1& x, const T2& y);template&l…...
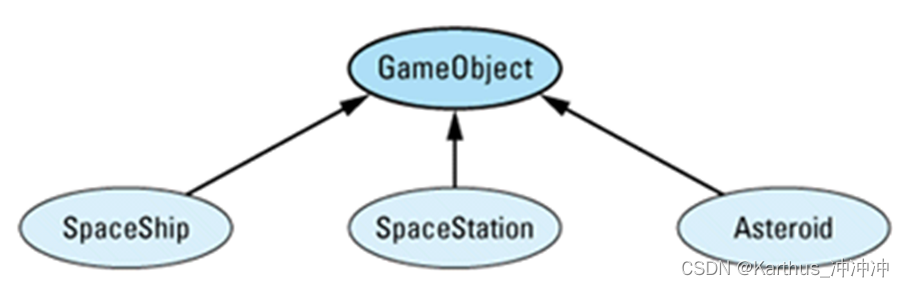
More Effective C++学习笔记(5)
目录 条款25:将构造函数和非成员函数虚化条款26:限制某个类所能产生的对象数量条款27:要求(或禁止)对象产生于heap(堆)之中条款28:智能指针条款29:引用计数条款30&#x…...
SpringMVC之CRUD(直接让你迅速完成部署)
一、项目创建 首先创建一个基于maven的项目部署,如果有些插件没有的话可以参考mybatis入门Idea搭建 二、配置依赖导入 依赖导入 1、pom.xml 需要根据自己的文件来进行导入,并不是原本照着导入 <project xmlns"http://maven.apache.org/POM/4.0.0…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...
