【数据结构与算法】数据结构的基本概念,时间复杂度
🍉内容专栏:【数据结构与算法】
🍉本文脉络:数据结构和算法的基本概念,时间复杂度
🍉本文作者:Melon西西
🍉发布时间 :2023.2.21
目录
一、引入:
二、数据结构和算法的基本概念
1.数据:
2.数据元素和数据项
3.数据结构
4.四类基本结构:
(1)集合结构:数据元素间属于同一个集合,如果不考虑元素间的关系,则称为集合结构。
(2)线性机构:一个对应一个的关系。
(3)树状结构:一个对应着多个的关系。
(4)图状结构:多个对应多个的关系。
5.存储结构
6.数据类型:
7.抽象数据类型(ADT):包括数据,关系,算法
8.算法:解决问题的操作步骤
9.算法的性质:正确性,具体性(可行性),确定性,有限性(有穷性),可读性,健壮性。
三、算法分析:时间复杂度和空间复杂度
1.时间复杂度T(n)=O(f(n)):
2.空间复杂度S(n)=O(f(n)):
一、引入:
对于数值计算问题的解决方法,主要用数学方程建立数学模型;而对于非数值计算问题,可以用数据结构的方法建立模型。
数据结构:研究如何高校的对数据进行操作(有大量数据的情况下)
三种结构:
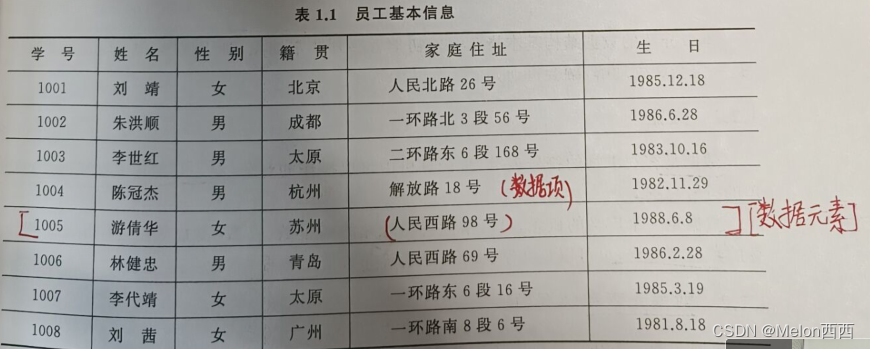
1.线性表结构(一个数据紧接着另一个数据):
其中一横行的内容叫数据元素,里面的每一小个内容叫数据项。
2.树性结构
3.图状结构
二、数据结构和算法的基本概念
1.数据:
数据是一切能输入计算机并被处理的符号总称,分为数值型数据和非数值型数据(如文字,图形,语音等)
2.数据元素和数据项
数据元素一般在计算机中作为整体进行处理,是数据的节能单位。
数据元素也称为记录,由若干个数据项组成,数据项是不能分割的最小单位。
3.数据结构
不同数据元素之间不是独立的,他们彼此之间存在特定的关系,这些关系称为结构(数据结构关系特指相邻关系)。
数据结构是相互存在着一定关系的数据元素的集合。
4.四类基本结构:
(1)集合结构:数据元素间属于同一个集合,如果不考虑元素间的关系,则称为集合结构。
(2)线性机构:一个对应一个的关系。
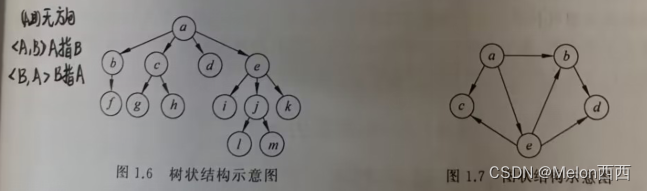
(3)树状结构:一个对应着多个的关系。
(4)图状结构:多个对应多个的关系。
图状结构的数据结构可以定义为如下的二元组:
DataStructure=(D,S) D是它的数据,S是逻辑结构

5.存储结构
存储结构分为顺序存储和链式存储
逻辑上相邻即位置上也相邻为顺序存储,反之为链式存储。
6.数据类型:
是指一组性质相同的值的集合以及定义在此几何上的一些操作的总称
7.抽象数据类型(ADT):包括数据,关系,算法
8.算法:解决问题的操作步骤
9.算法的性质:正确性,具体性(可行性),确定性,有限性(有穷性),可读性,健壮性。
三、算法分析:时间复杂度和空间复杂度
1.时间复杂度T(n)=O(f(n)):
算法执行时间=执行次数x执行一次的时间=基本语句的执行次数
基本语句:循环最内层的那条语句
执行次数看n,可忽略所有低次幂项和最高次幂系数
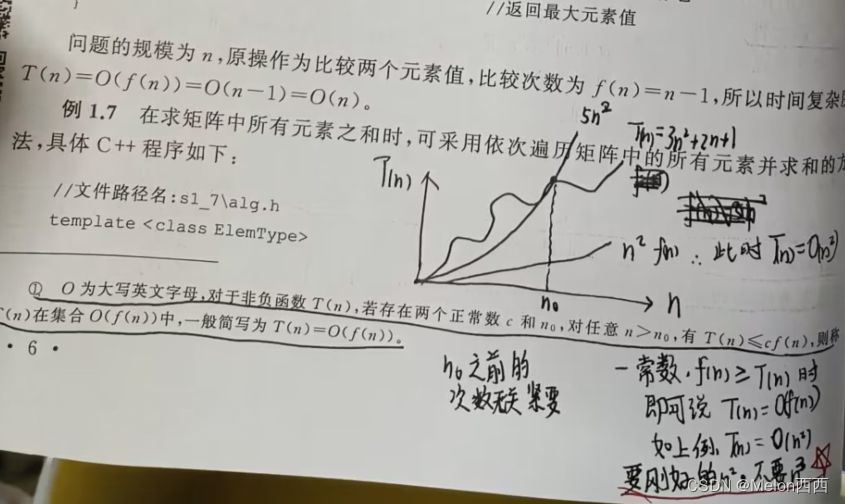

2.空间复杂度S(n)=O(f(n)):
写在最后:
相关文章:

【数据结构与算法】数据结构的基本概念,时间复杂度
🍉内容专栏:【数据结构与算法】 🍉本文脉络:数据结构和算法的基本概念,时间复杂度 🍉本文作者:Melon西西 🍉发布时间 :2023.2.21 目录 一、引入: 二、数据结…...

【Python】变量类型,赋值+多个变量赋值
嗨害大家好鸭~我是小熊猫(✿◡‿◡) 好像还有一些小伙伴还不是很会python的基础鸭~ 没关系啦~这不是还有我小熊猫嘛 ~ 源码资料电子书:点击此处跳转文末名片获取 Python 变量类型 变量是存储在内存中的值, 这就意味着在创建变量时会在内存中开辟一个空间。 基于…...

Qt基础之二十九:图形视图框架(Graphics View Framework)及其应用
无意中从网络获取一份俄罗斯方块源码,基于图形视图框架(Graphics View Framework)实现的。当然源码的核心从来都不是界面,而是方块的移动、变形和消除等算法。源码非常完整,注释详细,经改动后已能在Qt5中运行,下面是运行效果,背景音乐和音效也是有的。 一.效果 二.原理 …...
电商平台销量查询:2023年1月牛奶乳品热门排行榜
随着人们消费能力的提升以及健康意识的增强,牛奶乳品已经成为居民日常饮食中的重要组成部分,伴随人们整体消费的增长,牛奶乳品行业也越来越成熟。 今年1月份我国牛奶乳品行业的整体趋势如何呢?结合数据我们一同来分析!…...
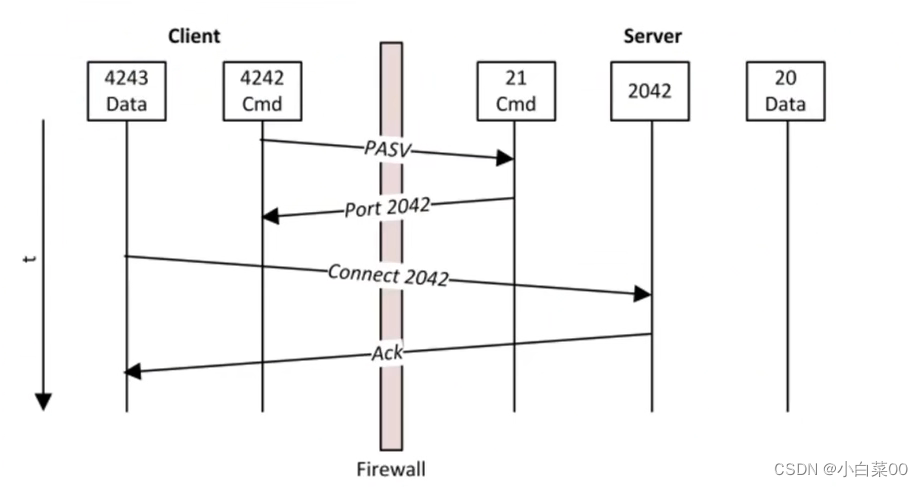
应用层协议
目录 应用层常见协议 DNS协议 前言 域名结构 DNS服务器分类 DNS的工作原理 DNS工作原理实例 DNS记录 DHCP协议 静态IP与动态IP DHCP协议好处 DHCP分配IP地址的4阶段 电子邮件 邮件的过程 电子邮件发送过程 pop协议特点 IMAP协议的特点 FTP协议 前言 FTP数据…...

Golang调用FFmpeg转换视频流
问题背景 问题背景是在,由于视频采集端使用的是H264编码采集的裸流,而网络流媒体大多是以FLV为主的直播方式进行的,为了实现实时直播,当前是打算直接使用FFmpeg将H264裸流实时转成FLV视频流。 为什么是使用FLV视频流呢,…...

外卖点餐小程序开发
前言 餐饮行业是一个传统的行业。根据当前发展现状,网络信息时代的全面普及,餐饮行业也在发生着变化,单就点餐这一方面,利用手机点单正在逐步进入人们的生活。传统的点餐方式,不仅会耗费大量的人力、时间,有时候还会出错。小程序系统伴随智能手机为我们提供了新的方向。 手机…...
)
华为OD机试真题Python实现【猴子爬山】真题+解题思路+代码(20222023)
猴子爬山 题目 一天一只顽猴想要从山脚爬到山顶, 途中经过一个有n个台阶的阶梯, 但是这个猴子有个习惯,每一次只跳1步或3步 试问?猴子通过这个阶梯有多少种不同的跳跃方式 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 输入 输入只…...
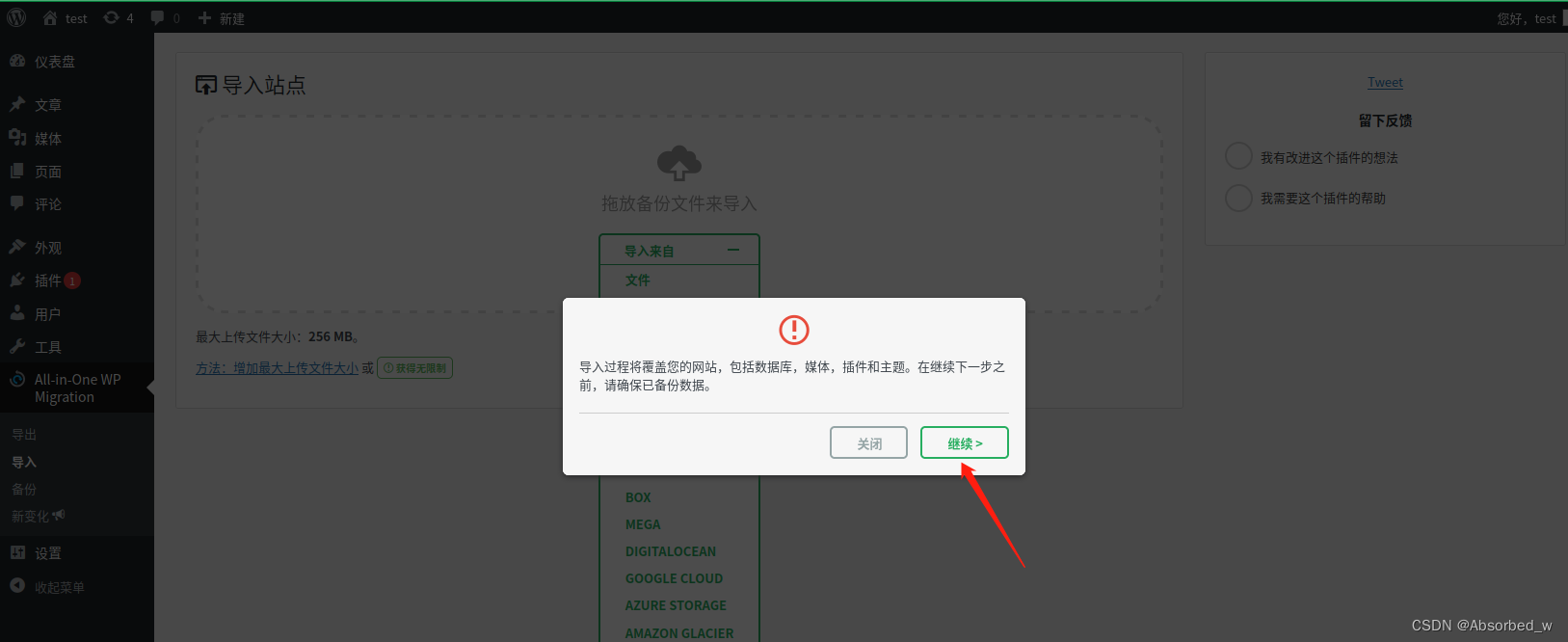
wordpress 网站备份
一个网站从建站完成之日,备份的问题就要提上日程。不论是后期的更换服务器,更换域名,未知故障导致网站崩溃,数据丢失,只要我们有完整的备份,就能将损失降到最低。wordpress网站的备份方法多种多样ÿ…...
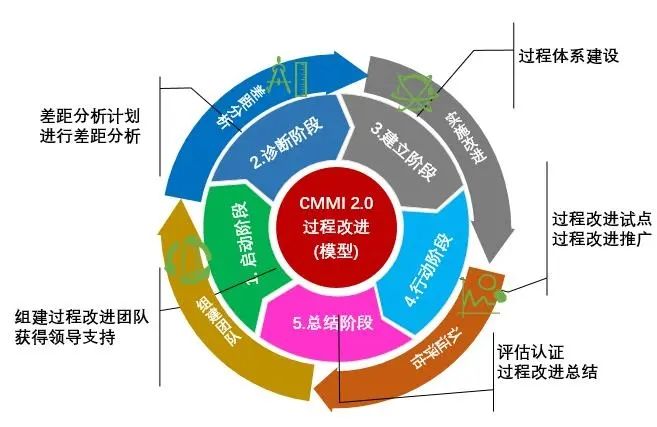
如何尽早解决需求变更隐患,降低项目延期风险?
频繁的需求变更,在早期我们应该如何尽早解决需求变更隐患,降低项目延期风险? 1、科学分析获取真实需求 建立需求基线 科学分析用户需求,颗粒度越小越好。需要提前建立需求基线,需求基线是需求变更的依据,并…...

[机缘参悟-96] :软件中到处充满了人类社会的气息!
解读操作系统有感:CPU对于CPU内核而言,调度程序是程序,应用程序也是程序,在它眼里是一样的、公平看待的,因此某种愿意上讲,CPU内核本身就是“上天”,就是“道”,道德经中讲“天地不仁…...

知识点滴 - 自行车分类
旅行车 旅行自行车(Touring bicycle)由公路自行车发展而来,适合超远程自给自足的旅行,有较舒适放松的车架几何设计,能够负重,有很低的最低档位,配件选择方面追求可靠耐用。 专业的长途旅行车均以…...

【建议收藏】Jenkins+postman+newman之API全自动化测试
1 背景 本文要介绍的环境在我司已经投入使用,举个简单的真实使用场景,开发提供了300多个API,每个API都有各种参数,所以我们会先在postman中为这300多个API编写300*n个testcase,然后在jenkins上跑;到此有人…...

MySQL数据库————MVCC
MySQL的脏读、幻读、不可重复读 脏读 现在有两个事务在操作table表,事务B修改了id2的name字段为李老四,但是没有提交,事务A查询id2的数据,得到name为李老四;事务B发生回滚,id2的数据的name又变回李四&…...

为啥Python多线程爬虫跑的慢?
单线程和多线程进行数据抓取结果还是大有不同的,但是要值得注意的事,如果多线程没调配好可能连单线程的效率都比不上。本次就和大家一起聊一聊单线程多线程的一些需要注意的事项。 知识点 线程(Thread)也叫轻量级进程࿰…...
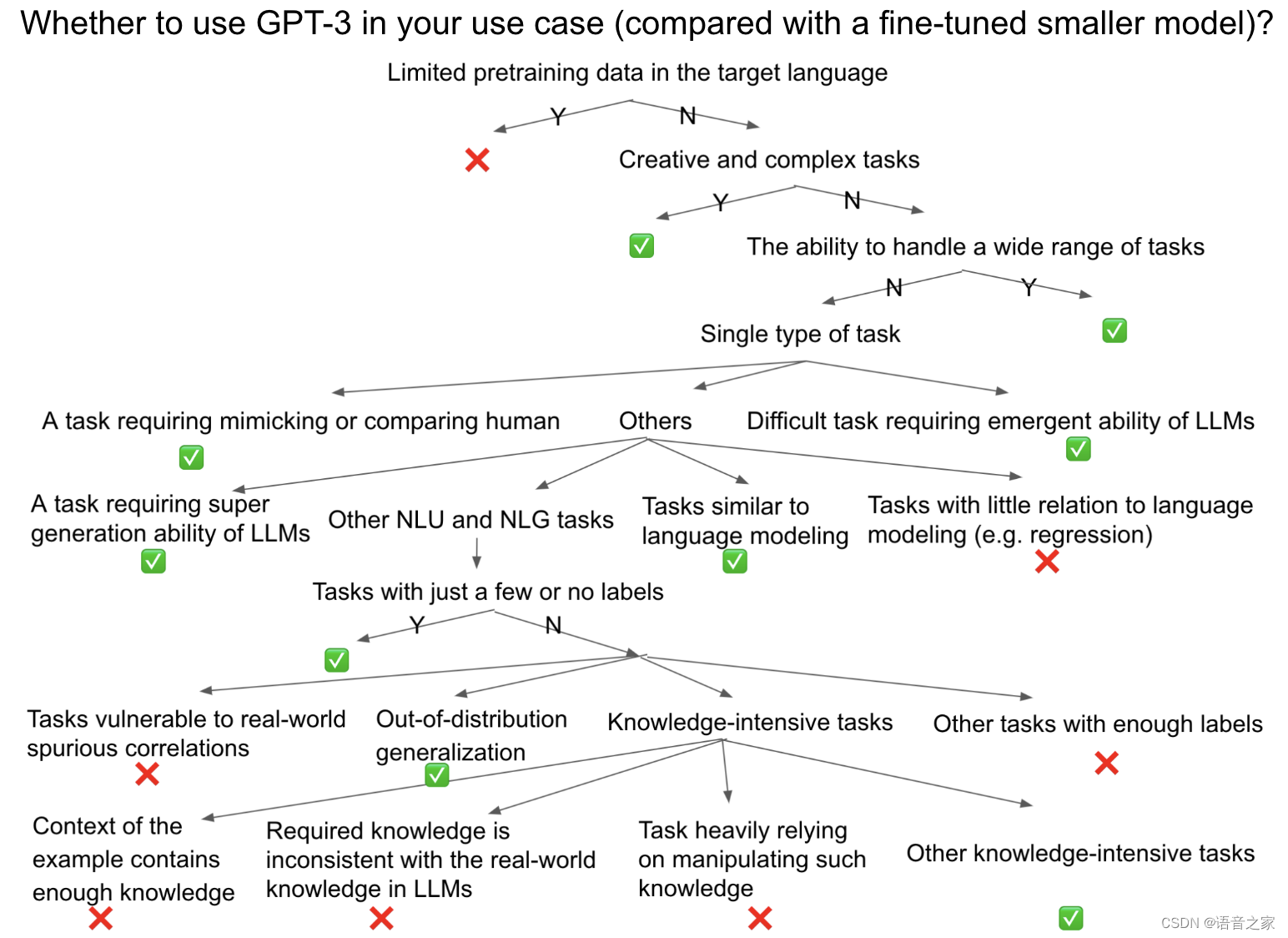
万字长文解析!复现和使用GPT-3/ChatGPT,你所应该知道的
关于作者 英文原版作者:杨靖锋,现任亚马逊科学家,本科毕业于北大,硕士毕业于佐治亚理工学院,师从 Stanford 杨笛一教授。 杨昊桐 译,王骁 修订 感谢靳弘业对第一版稿件的建议,感谢陈三星&am…...
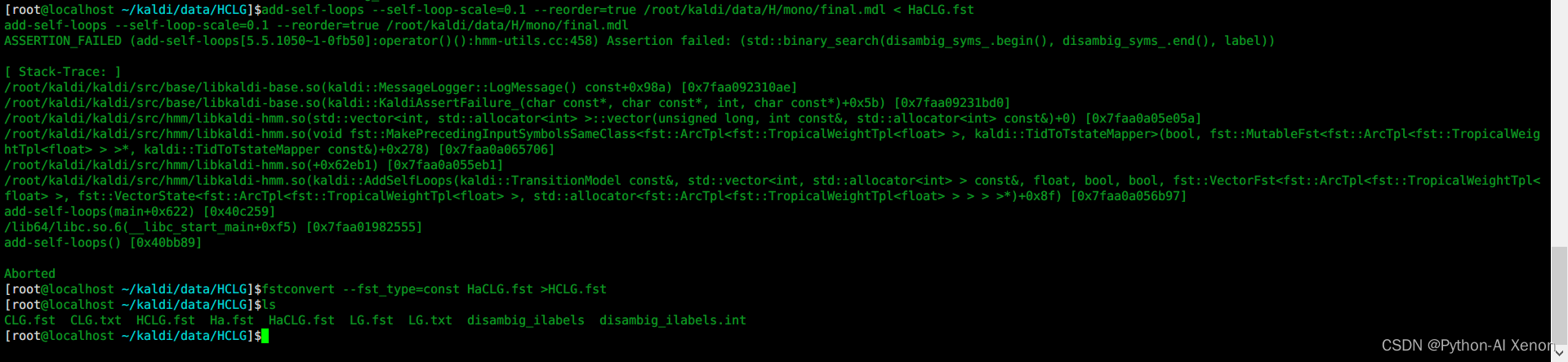
Kaldi语音识别技术(八) ----- 整合HCLG
Kaldi语音识别技术(八) ----- 整合HCLG 文章目录Kaldi语音识别技术(八) ----- 整合HCLGHCLG 概述组合LG.fst可视化 LG.fst组合CLG.fst可视化CLG.fst生成H.fst组合HCLG.fst生成HaCLG.fst生成HCLG.fstHCLG 概述 HCLG min(det(H o min(det(C o min(det(L o G))))) 将…...
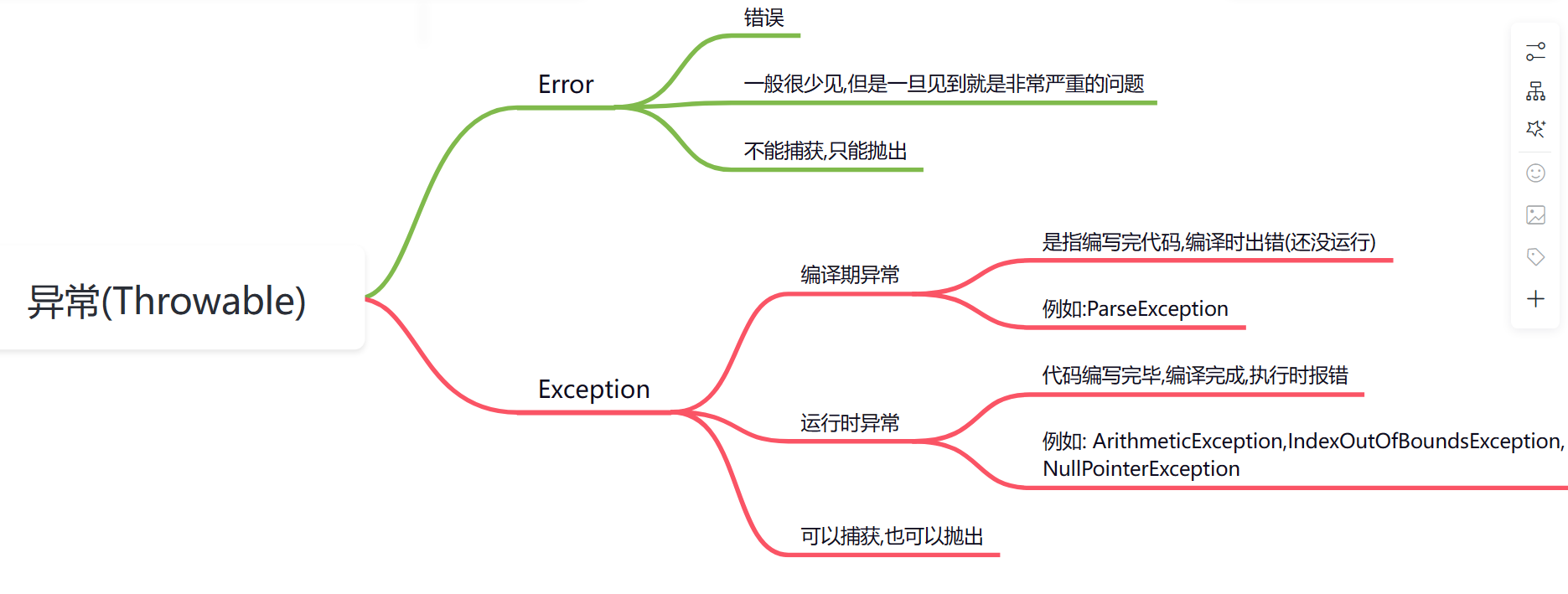
day17_异常
今日内容 上课同步视频:CuteN饕餮的个人空间_哔哩哔哩_bilibili 同步笔记沐沐霸的博客_CSDN博客-Java2301 零、 复习昨日 一、作业 二、异常 三、自定义异常 零、 复习昨日 见晨考 一、作业 package com.qf.homework;import java.text.ParseException; import java.text.Simpl…...
)
vue中把node-sass换成dart-sass方式(解决办法)
目录 一、替换原因 二、art-sass和node-sass的区别 三、替换方法 一、替换原因 因为node-sass和node.js版本关联太紧了,如果这两个版本不匹配,就会起冲突,导致项目无法运行。 ps:值得一提的是node版本和要运行的项目使用的依…...
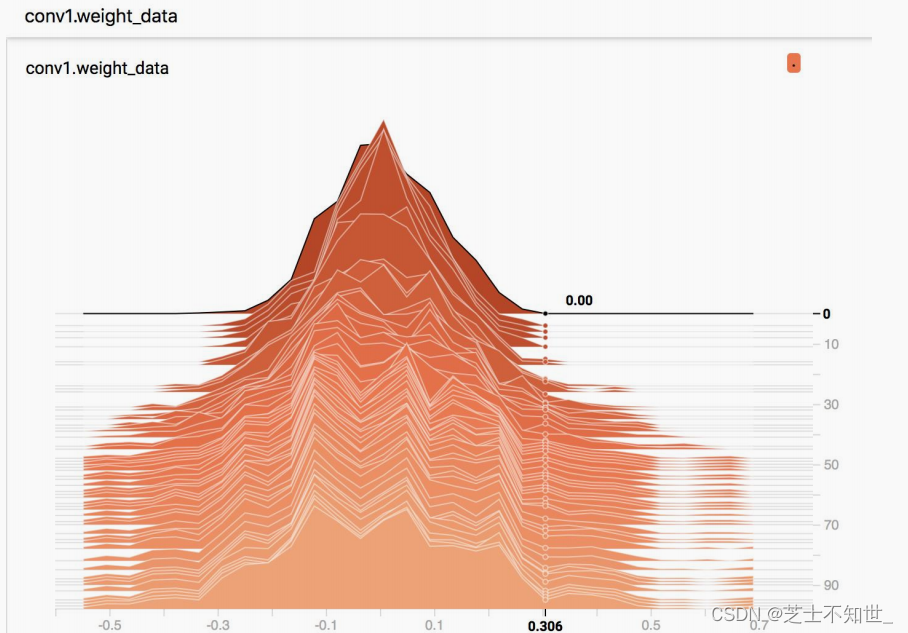
深入浅出深度学习Pytroch
本文将以通俗易懂的方式,深入浅出地为您揭开深度学习模型构建与训练的面纱: 深度学习数据data模型model损失函数loss优化optimizer可视化visualizer深度学习 数据data 模型model 损失函数loss 优化optimizer 可视化visualizer深度学习数据data模型m…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...