【无标题】10.货币系统
题目描述:
在网友的国度中共有 n 种不同面额的货币,第 i 种货币的面额为 a[i],你可以
假设每一种货币都有无穷多张。为了方便,我们把货币种数为 n、 面额数组为 a[1..n]
的货币系统记作 (n,a)。
在一个完善的货币系统中,每一个非负整数的金额 x 都应该可以被表示出,即对
每一个非负整数 x,都存在 n 个非负整数 t[i] 满足 a[i]× t[i] 的和为 x。然而,
在网友的国度中, 货币系统可能是不完善的,即可能存在金额 x 不能被该货币系统表
示出。例如在货币系统 n=3, a=[2,5,9] 中,金额 1,3 就无法被表示出来。
两个货币系统 (n,a) 和 (m,b) 是等价的, 当且仅当对于任意非负整数 x,它要
么均可以被两个货币系统表出,要么不能被其中任何一个表出。
现在网友们打算简化一下货币系统。 他们希望找到一个货币系统 (m,b),满足
(m,b) 与原来的货币系统 (n,a) 等价,且 m 尽可能的小。他们希望你来协助完成这
个艰巨的任务:找到最小的 m。
输入格式:
输入文件名为 money.in。
输入文件的第一行包含一个整数 T, 表示数据的组数。 接下来按照如下格式分别给
出 T 组数据。
每组数据的第一行包含一个正整数 n。接下来一行包含 n 个由空格隔开的正整数
a[i]。
输出格式:
输出文件名为 money.out。
输出文件共有 T 行, 对于每组数据,输出一行一个正整数,表示所有与 (n,a) 等
价的货币系统 (m,b) 中,最小的 m。
样例输入:
2 4 3 19 10 6 5 11 29 13 19 17
样例输出:
2 5
提示:
在第一组数据中,货币系统 (2, [3,10]) 和给出的货币系统 (n, a) 等价,并
可以验证不存在 m < 2 的等价的货币系统,因此答案为 2。
在第二组数据中,可以验证不存在 m < n 的等价的货币系统,因此答案为 5。
【数据规模与约定】
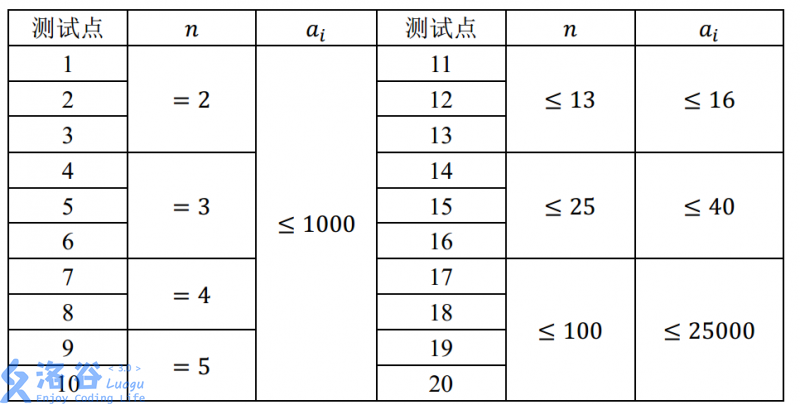
对于 100% 的数据,满足 1 ≤ T ≤ 20, n,a[i] ≥ 1。
时间限制: 1500ms
空间限制: 512MB
代码:
#include<bits/stdc++.h>
using namespace std;int t;//组数
int n;
int *a;
int vis[25010];
int ans;int main()
{cin>>t;for(int i=0;i<t;i++){ans=0;cin>>n;// n 种不同面额的货币a=new int[n];memset(vis,0,sizeof(vis));for(int j=0;j<n;j++){cin>>a[j];}//这些货币所能表示的所有数字//都能被新的货币系统表示 //等价 //质数 如果a[i]能被a 中数表示出来 就减去它//这像是线性相关sort(a,a+n);//从小到大排序//完全背包for(int k=0;k<n;k++){if(vis[a[k]]==0){ans++;vis[a[k]]=1;}for(int m=a[k];m<=a[n-1];m++){vis[m]|=vis[ m-a[k] ];}}cout<<ans<<endl;//输出一行 所有与(n,a)等价的货币系统(m,b)中,最小的m delete a;//delete vis;}return 0;
}相关文章:

【无标题】10.货币系统
题目描述: 在网友的国度中共有 n 种不同面额的货币,第 i 种货币的面额为 a[i],你可以 假设每一种货币都有无穷多张。为了方便,我们把货币种数为 n、 面额数组为 a[1..n] 的货币系统记作 (n,a)。 在一个完善的货币系统中,每一个非…...

【c++】类和对象6—运算符重载
文章目录加号()运算符重载左移(<<)运算符重载递增()运算符重载赋值()运算符重载关系运算符重载函数调用运算符重载运算符重载概念: 对已有的运算符重新进行定义&am…...
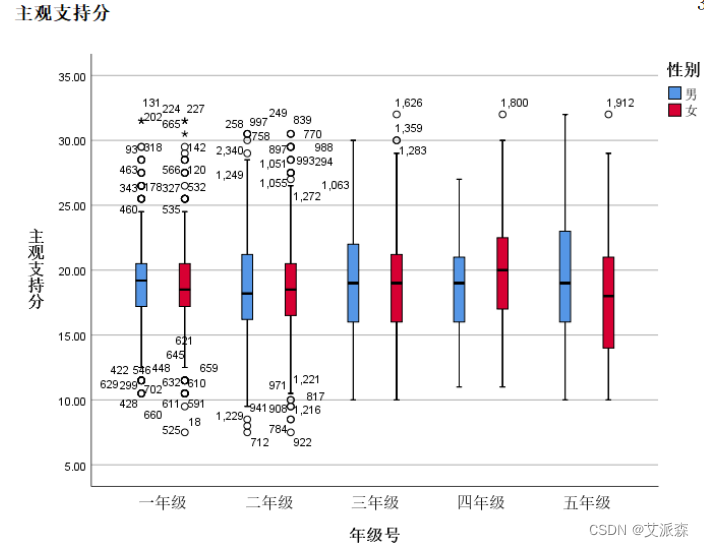
【SPSS】基础图形的绘制(条形图、折线图、饼图、箱图)详细操作过程
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...

6、Fatfs系统移植
注意:挂载Fatfs笔记 Fatfs系统读写文件的时间是不固定的,随机性 搭载Fatfs的外设通信方式建议开启DMA方式,否则应避免中断打断时序,导致Fatfs出现FR_DISK_ERR(A hard error occurred in the low level disk I/O layer&…...

【数据结构与算法】数据结构的基本概念,时间复杂度
🍉内容专栏:【数据结构与算法】 🍉本文脉络:数据结构和算法的基本概念,时间复杂度 🍉本文作者:Melon西西 🍉发布时间 :2023.2.21 目录 一、引入: 二、数据结…...

【Python】变量类型,赋值+多个变量赋值
嗨害大家好鸭~我是小熊猫(✿◡‿◡) 好像还有一些小伙伴还不是很会python的基础鸭~ 没关系啦~这不是还有我小熊猫嘛 ~ 源码资料电子书:点击此处跳转文末名片获取 Python 变量类型 变量是存储在内存中的值, 这就意味着在创建变量时会在内存中开辟一个空间。 基于…...

Qt基础之二十九:图形视图框架(Graphics View Framework)及其应用
无意中从网络获取一份俄罗斯方块源码,基于图形视图框架(Graphics View Framework)实现的。当然源码的核心从来都不是界面,而是方块的移动、变形和消除等算法。源码非常完整,注释详细,经改动后已能在Qt5中运行,下面是运行效果,背景音乐和音效也是有的。 一.效果 二.原理 …...
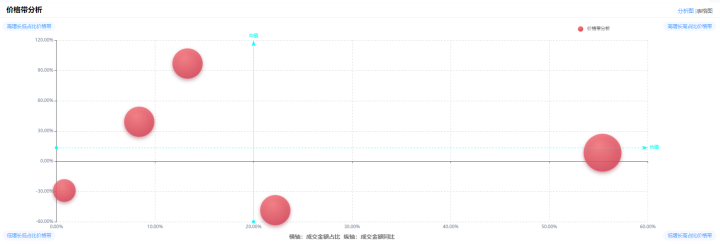
电商平台销量查询:2023年1月牛奶乳品热门排行榜
随着人们消费能力的提升以及健康意识的增强,牛奶乳品已经成为居民日常饮食中的重要组成部分,伴随人们整体消费的增长,牛奶乳品行业也越来越成熟。 今年1月份我国牛奶乳品行业的整体趋势如何呢?结合数据我们一同来分析!…...
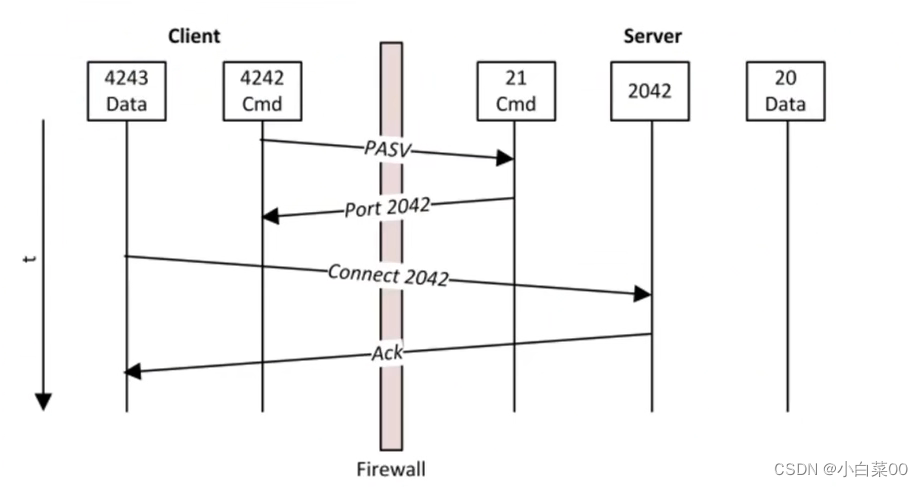
应用层协议
目录 应用层常见协议 DNS协议 前言 域名结构 DNS服务器分类 DNS的工作原理 DNS工作原理实例 DNS记录 DHCP协议 静态IP与动态IP DHCP协议好处 DHCP分配IP地址的4阶段 电子邮件 邮件的过程 电子邮件发送过程 pop协议特点 IMAP协议的特点 FTP协议 前言 FTP数据…...

Golang调用FFmpeg转换视频流
问题背景 问题背景是在,由于视频采集端使用的是H264编码采集的裸流,而网络流媒体大多是以FLV为主的直播方式进行的,为了实现实时直播,当前是打算直接使用FFmpeg将H264裸流实时转成FLV视频流。 为什么是使用FLV视频流呢,…...

外卖点餐小程序开发
前言 餐饮行业是一个传统的行业。根据当前发展现状,网络信息时代的全面普及,餐饮行业也在发生着变化,单就点餐这一方面,利用手机点单正在逐步进入人们的生活。传统的点餐方式,不仅会耗费大量的人力、时间,有时候还会出错。小程序系统伴随智能手机为我们提供了新的方向。 手机…...
)
华为OD机试真题Python实现【猴子爬山】真题+解题思路+代码(20222023)
猴子爬山 题目 一天一只顽猴想要从山脚爬到山顶, 途中经过一个有n个台阶的阶梯, 但是这个猴子有个习惯,每一次只跳1步或3步 试问?猴子通过这个阶梯有多少种不同的跳跃方式 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 输入 输入只…...
wordpress 网站备份
一个网站从建站完成之日,备份的问题就要提上日程。不论是后期的更换服务器,更换域名,未知故障导致网站崩溃,数据丢失,只要我们有完整的备份,就能将损失降到最低。wordpress网站的备份方法多种多样ÿ…...
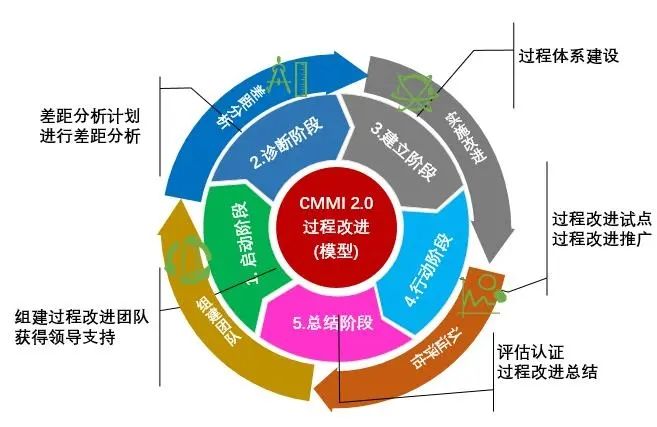
如何尽早解决需求变更隐患,降低项目延期风险?
频繁的需求变更,在早期我们应该如何尽早解决需求变更隐患,降低项目延期风险? 1、科学分析获取真实需求 建立需求基线 科学分析用户需求,颗粒度越小越好。需要提前建立需求基线,需求基线是需求变更的依据,并…...

[机缘参悟-96] :软件中到处充满了人类社会的气息!
解读操作系统有感:CPU对于CPU内核而言,调度程序是程序,应用程序也是程序,在它眼里是一样的、公平看待的,因此某种愿意上讲,CPU内核本身就是“上天”,就是“道”,道德经中讲“天地不仁…...

知识点滴 - 自行车分类
旅行车 旅行自行车(Touring bicycle)由公路自行车发展而来,适合超远程自给自足的旅行,有较舒适放松的车架几何设计,能够负重,有很低的最低档位,配件选择方面追求可靠耐用。 专业的长途旅行车均以…...

【建议收藏】Jenkins+postman+newman之API全自动化测试
1 背景 本文要介绍的环境在我司已经投入使用,举个简单的真实使用场景,开发提供了300多个API,每个API都有各种参数,所以我们会先在postman中为这300多个API编写300*n个testcase,然后在jenkins上跑;到此有人…...

MySQL数据库————MVCC
MySQL的脏读、幻读、不可重复读 脏读 现在有两个事务在操作table表,事务B修改了id2的name字段为李老四,但是没有提交,事务A查询id2的数据,得到name为李老四;事务B发生回滚,id2的数据的name又变回李四&…...

为啥Python多线程爬虫跑的慢?
单线程和多线程进行数据抓取结果还是大有不同的,但是要值得注意的事,如果多线程没调配好可能连单线程的效率都比不上。本次就和大家一起聊一聊单线程多线程的一些需要注意的事项。 知识点 线程(Thread)也叫轻量级进程࿰…...
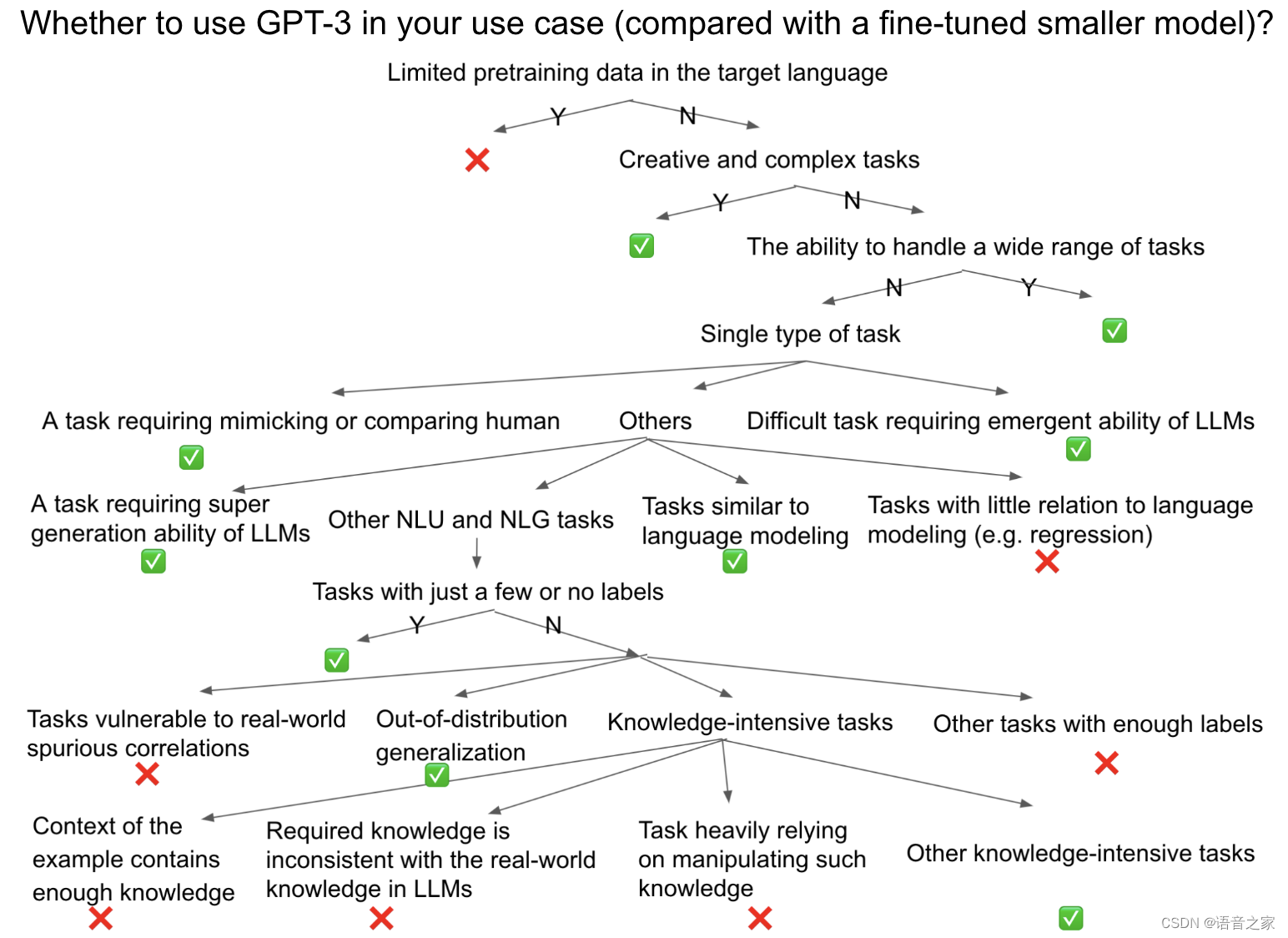
万字长文解析!复现和使用GPT-3/ChatGPT,你所应该知道的
关于作者 英文原版作者:杨靖锋,现任亚马逊科学家,本科毕业于北大,硕士毕业于佐治亚理工学院,师从 Stanford 杨笛一教授。 杨昊桐 译,王骁 修订 感谢靳弘业对第一版稿件的建议,感谢陈三星&am…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...
