【C++】详解红黑树并模拟实现
前言:
上篇文章我们一起学习了AVL树比模拟实现,我们发现AVL树成功地把时间复杂度降低到了O(logN)。但是同时我们不难发现一个问题,在构建AVL树中我们也付出了不小的代价,频繁的旋转操作导致效率变低。为了解决这个问题,我们本章将迎来更为实用的红黑树,他在提高查找效率的同时也相对AVL树提高了构建树的效率,他的应用将更加广泛(比如map、set的底层实现就是红黑树)!
目录
(一)红黑树的概念
1、概念
2、特性
(二)红黑树的模拟实现
1、结点的定义
2、结点的查找实现(Find)
3、结点的插入实现(Insert)*重点
3.1前序问题
3.2具体流程
情况一:叔叔存在且为红——变色处理
情况二:叔叔不存在or叔叔存在且为黑——旋转+变色
情况三:叔叔不存在or叔叔存在且为黑——双旋+变色(区别于情况二)
4、具体代码(Find+Insert)
(三)验证红黑树
1、中序遍历
2、验证红黑树几大特性
3、测试用例
(四)项目完整代码
(一)红黑树的概念
1、概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black,所以叫红黑树。
通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
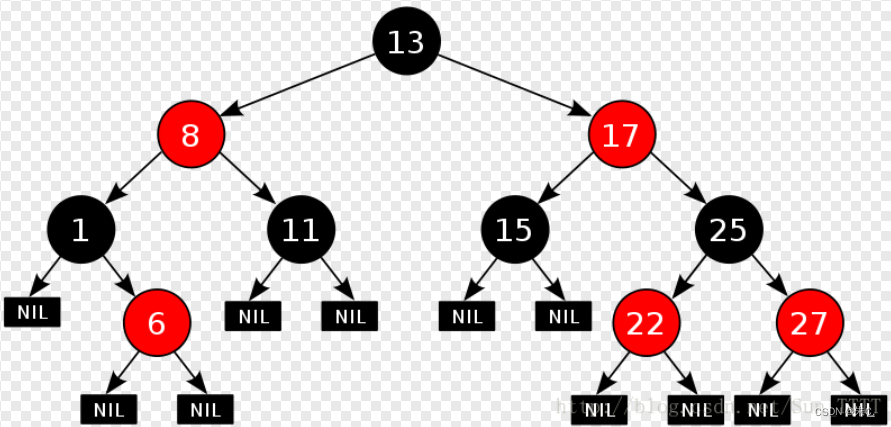
2、特性
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
思考:
这条路径一个黑色节点接着一个红色节点,交相出现:

这时我们发现最短路径时,一条路径上有三个结点(情况一);最长路径时,一条路径上有五个节点(情况二)。所以可以保证其最长路径中节点个数不会超过最短路径节点个数的两倍。
(二)红黑树的模拟实现
1、结点的定义
我们还是沿用AVL树节点的三叉链定义方法,颜色我们用枚举来实现:
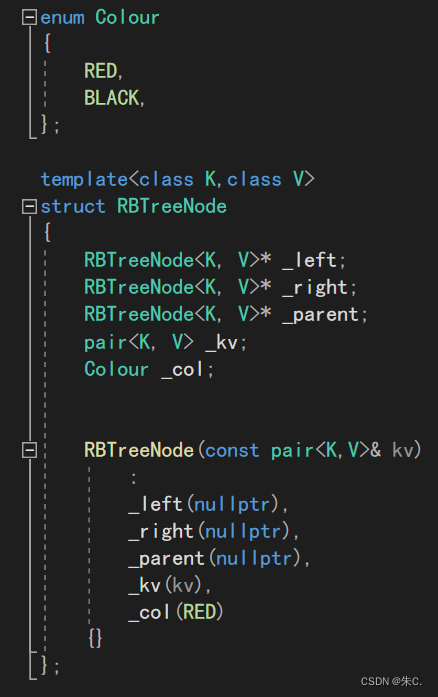
ps:这里一开始结点定义为红色的原因,我们在后文插入的时候会详细讲解。
2、结点的查找实现(Find)
在红黑树中的Find(查找)操作和之前二叉搜索树和AVL树实现方法一样,这里我们简单带过。
结点存的值比当前结点小就向左找,比当前结点大就向右找,最后遇到空节点表示没找到。

3、结点的插入实现(Insert)*重点
3.1前序问题
首先,我们解答上面留下的那个问题,
为什么新插入的结点要默认给红色的?
- 假设我们默认给新增的结点黑色,那么一定违反上面红黑树的特性4(对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点 )。这样我们还要对其他路径进行修改黑色结点的数量。
- 但是如果默认给红色,我们则是可能违反特性3(如果一个节点是红色的,则它的两个孩子结点是黑色的 )。为什么说是可能,因为如果他的父亲节点是黑色则不违反。就算违反了。每条路径黑色结点的数量还是一样的,我们只需要调整所在的那一条路径即可,代价相对小了许多。
3.2具体流程
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
(分别对应parent,grandfather,uncle的意思)
插入几大流程:
- 按照搜索二叉树的查找方法,找到要插入的位置
- 将新增结点插入到待插入位置
- 如果需要调整则调整红黑树
其中需不需要调整主要是看叔叔颜色的情况。
下面具体分析:
我们先给出一个基本的图示

这里的三角形就相当于AVL树中的小长方形,代表了一部分子树。
情况一:叔叔存在且为红——变色处理
- cur为红,p为红,g为黑, u存在且为红
解决方式:将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。
首先我们知道,红黑树调整主要看叔叔,第一步我们将父亲变成黑色,为了维护性质4,我们也要将叔叔的颜色变成黑色,同时也要将祖父结点的颜色变成红色,因为我们此时处理的不一定是整棵树,有可能是某个子树,如果此时不是子树,就需要将根节点变成黑色。这样我们就在局部调整颜色并保证了不破坏规则。
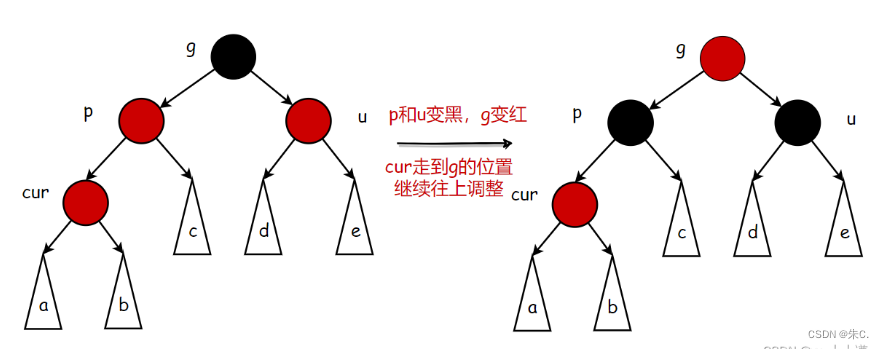
调整的部分可能是一整棵树,也可能是某一棵子树
- 如果g是根节点,调整完成后,需要将g改为黑色
- 如果g是子树,g一定有双亲,且g的双亲如果是红色,需要继续向上调整

情况一的情景下,我们只关心颜色的调整就可以在不破坏规则的情况下插入结点!
情况二:叔叔不存在or叔叔存在且为黑——旋转+变色

情况二可能就是从情况一调整变化得到的情况。
当叔叔不存在时:
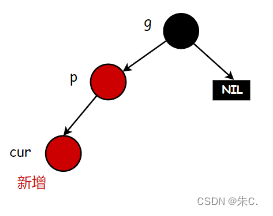
我们调整颜色总会破坏规则,此时结合上面长路径不会超过短路径二倍的特性我们分析,英爱使用到了和AVL树相似的旋转处理。
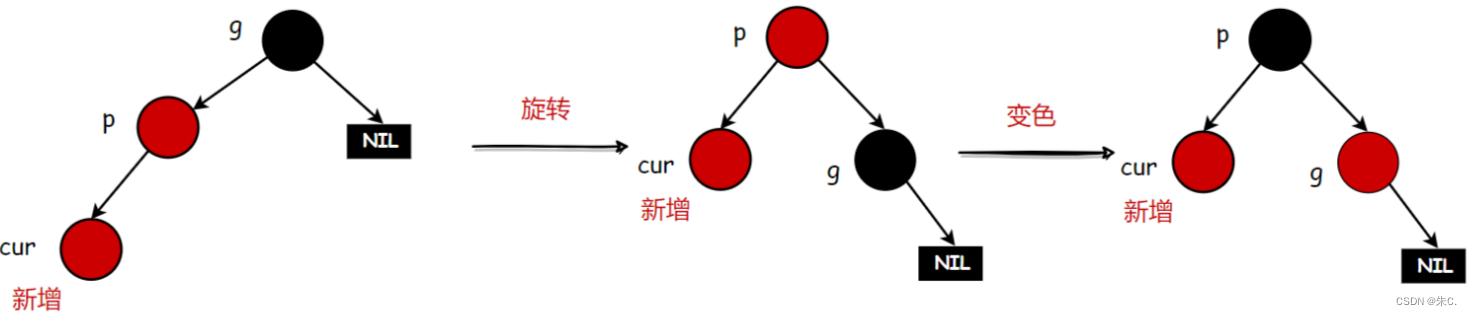
- 此时是左边高了,我们对图示树进行右单旋,这里的旋转和AVL树中旋转的方式如出一辙,可以拿过来直接复用。
- 同样的道理,如果是右边高了,我们就可以进行左单旋,旋转的方法也和AVL树中的如出一辙,也可拿过来直接复用。(这里我们就不像AVL树那样详细解释了,实现方法是一样的,如果读者不太了解可以看上一篇文章)
具体情况 2
当叔叔存在且为黑时:
按照上文说明,这种情况必定是由情况一变化而来的。
此时也是旋转+变色
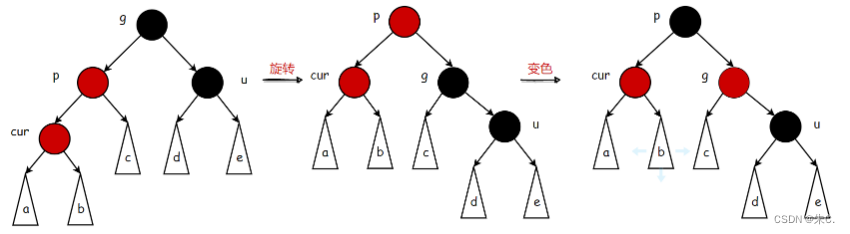
这样子才能保护好红黑树的结构。
情况三:叔叔不存在or叔叔存在且为黑——双旋+变色(区别于情况二)
同样是 叔叔不存在 or 叔叔存在且为黑,为啥分为情况二和情况三呢?
上述旋转的情况都是单边的情况,也就是说,cur、p、g在一条线上的情况,若是出现了这三者不在一条直线的时候,单旋就解决不了问题了。
区别:
- p是g的左,cur是p的左,那么是情况二 —— 单旋
- p是g的左,cur是p的右,那么是情况三 —— 双旋
此时我们就引入了双旋
(这里我们可以结合上一篇AVL树来区别单旋和双旋)

- 先以p为旋转点再以g为旋转点
- 先变到情况二的样子
- 再根据情况二来继续变
其实看完情况二和三有些人就会有疑问了,看上去每条路径上黑色结点树不一样啊,为什么要这样旋转变色?
再此之前我们推测过当叔叔存在且为黑时,一定是由情况一变来的,所以cur一开始是黑的,这个树并不违反性质,子树由情况一变化之后的子树结点的颜色也相应变化了,只是没有显示出来而已。
4、具体代码(Find+Insert)
Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while(cur){ if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){ parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first>kv.first){parent->_left = cur;}else if (parent->_kv.first < kv.first){parent->_right = cur;}cur->_parent = parent;//调整颜色while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (grandfather->_left == parent)//u存在且为红{Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//u不存在或者为黑,旋转加变色{if (cur == parent->_left){// g// p u//cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// p u// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else//grandfather->_right == parent{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){// g// u p// cuncle->_col = BLACK;parent->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else// :u不存在/u存在且为黑,旋转+变色{if (cur == parent->_right){// g// u p// cRotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// u p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}
(三)验证红黑树
老样子,我们在上一章模拟实现AVL树后用了几个函数来验证我们构建的树是否是AVL树,这里我们也要验证一下我们构建的这棵树是否是红黑树。
几个验证要点:
- 这棵树是否是二叉搜索树
- 根结点是否是黑色结点
- 红色结点的子结点是否是黑色结点
- 每条路径黑色结点树是否一样
满足这几个要点,也就是红黑树的特性,那么这棵树1就是红黑树了。
1、中序遍历
一棵树是红黑树的前提就是他必须是二叉搜索树,二叉搜索树的特点就是中序遍历是有序的。
void InOrder(){return _InOrder(_root);}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}ps:为了符合用户的使用习惯,我们还是采取嵌套的方式,大家不明白的可以看一下上一篇文章验证处有说明哦!
2、验证红黑树几大特性
相对AVL树,验证红黑树是更加麻烦的,几个要点:
- 首先判断根结点是否是黑色
- 判断每条路径黑色结点数我们思路是先取一条路径黑色结点数量为基准值,然后递归统计其他路径的数目,遇到空结点再比较
- 遇到红色结点我们如果判断他的孩子结点是否是黑色,如果是要跳过(代码不好写),不如换个思路,遇到一个红色结点就判断双亲是否是红色,如果是(存在连续红色结点)返回false。
bool IsBalance(){if (_root->_col == RED){cout << "根节点颜色是红色" << endl;return false;}int benchmark = 0;Node* cur = _root;while (cur){if(cur->_col==BLACK)benchmark++;cur = cur->_left;}return _Check(_root, 0, benchmark);}private:bool _Check(Node* root, int blackNum, int benchmark){if (root == nullptr){if (benchmark != blackNum){cout << "某条路径黑色节点的数量不相等" << endl;return false;}return true;}if (root->_col == BLACK){++blackNum;}if (root->_col == RED&& root->_parent&& root->_parent->_col == RED){cout << "存在连续的红色节点" << endl;return false;}return _Check(root->_left, blackNum, benchmark)&& _Check(root->_right, blackNum, benchmark);}通过递归的方式将每条支路都走了一遍和基准值比较,并且将红黑树的性质全都验证了。
3、测试用例
void Test_RBTree1()
{//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14, 16, 3, 7, 11, 9, 26, 18, 14, 15 };RBTree<int, int> t1;for (auto e : a){/* if (e == 14){int x = 0;}*/t1.Insert(make_pair(e, e));//cout << e << "插入:" << t1.IsBalance() << endl;}t1.InOrder();cout << endl;cout << t1.IsBalance() << endl;
}void Test_RBTree2()
{srand(time(0));const size_t N = 5000000;RBTree<int, int> t;for (size_t i = 0; i < N; ++i){size_t x = rand() + i;t.Insert(make_pair(x, x));//cout << t.IsBalance() << endl;}//t.Inorder();cout << t.IsBalance() << endl;cout << t.Height() << endl;
}精检验,没有问题:

(四)项目完整代码
#pragma once
#include<iostream>
#include<assert.h>using namespace std;enum Colour
{RED,BLACK,
};template<class K,class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K,V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED){}
};template<class K,class V>
struct RBTree
{typedef RBTreeNode<K, V> Node;void Destroy(Node* root){_Destroy(root);root = nullptr;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while(cur){ if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){ parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first>kv.first){parent->_left = cur;}else if (parent->_kv.first < kv.first){parent->_right = cur;}cur->_parent = parent;//调整颜色while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (grandfather->_left == parent)//u存在且为红{Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//u不存在或者为黑,旋转加变色{if (cur == parent->_left){// g// p u//cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// p u// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else//grandfather->_right == parent{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){// g// u p// cuncle->_col = BLACK;parent->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else// :u不存在/u存在且为黑,旋转+变色{if (cur == parent->_right){// g// u p// cRotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// u p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}void InOrder(){return _InOrder(_root);}int Height(){return _Height(_root);}bool IsBalance(){if (_root->_col == RED){cout << "根节点颜色是红色" << endl;return false;}int benchmark = 0;Node* cur = _root;while (cur){if(cur->_col==BLACK)benchmark++;cur = cur->_left;}return _Check(_root, 0, benchmark);}private:bool _Check(Node* root, int blackNum, int benchmark){if (root == nullptr){if (benchmark != blackNum){cout << "某条路径黑色节点的数量不相等" << endl;return false;}return true;}if (root->_col == BLACK){++blackNum;}if (root->_col == RED&& root->_parent&& root->_parent->_col == RED){cout << "存在连续的红色节点" << endl;return false;}return _Check(root->_left, blackNum, benchmark)&& _Check(root->_right, blackNum, benchmark);}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}int _Height(Node* root){if(root==nullptr){return 0;}int leftH = _Height(root->_left);int rightH = _Height(root->_right);return leftH > rightH ? leftH + 1 : rightH + 1;}void _Destroy(Node* root){if (root == nullptr)return;_Destroy(root->_left);_Destroy(root->_right);delete root;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppnode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (ppnode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppnode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}}
private:Node* _root=nullptr;
};void Test_RBTree1()
{//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14, 16, 3, 7, 11, 9, 26, 18, 14, 15 };RBTree<int, int> t1;for (auto e : a){/* if (e == 14){int x = 0;}*/t1.Insert(make_pair(e, e));//cout << e << "插入:" << t1.IsBalance() << endl;}t1.InOrder();cout << endl;cout << t1.IsBalance() << endl;
}void Test_RBTree2()
{srand(time(0));const size_t N = 5000000;RBTree<int, int> t;for (size_t i = 0; i < N; ++i){size_t x = rand() + i;t.Insert(make_pair(x, x));//cout << t.IsBalance() << endl;}//t.Inorder();cout << t.IsBalance() << endl;cout << t.Height() << endl;
}祝您学业有成!
相关文章:

【C++】详解红黑树并模拟实现
前言: 上篇文章我们一起学习了AVL树比模拟实现,我们发现AVL树成功地把时间复杂度降低到了O(logN)。但是同时我们不难发现一个问题,在构建AVL树中我们也付出了不小的代价,频繁的旋转操作导致效率变低。为了解决这个问题,…...

Matlab图像处理-最大类间方差阈值选择法(Otsu)
基本思想 最大类间方差阈值选择法又称为Otsu 算法,该算法是在灰度直方图的基础上用最小二乘法原理推导出来的,具有统计意义上的最佳分割阈值。它的基本原理是以最佳阈值将图像的灰度直方图分割成两部分,使两部分之间的方差取得最大值&#x…...
系列教程(三) 服务消费者(Feign))
Spring Cloud(Finchley版本)系列教程(三) 服务消费者(Feign)
Spring Cloud(Finchley版本)系列教程(三) 服务消费者(Feign) 一、Feign和OpenFeign的对比 Feign是Netflix公司写的,是SpringCloud组件中的一个轻量级RESTful的HTTP服务客户端,是SpringCloud中的第一代负载均衡客户端。OpenFeign是SpringCloud自己研发的,在Feign的基础上支…...
AI图片生成 discord 使用midjourney
参考: 不用找咒语了!Midjourney图生文功能特征解析,玩转Describe命令,快速搞定AI绘画_哔哩哔哩_bilibili 1 登录 discord 2 点发现 找 midjourney 3 创建 服务器 -> 亲自创建 4 选 仅供我和我的朋友使用 5 起个 服务器名字 6 加bot 由于…...
gitlab 点击Integrations出现500错误
背景:在新服务器重新搭建了gitlab,并导入原来gitlab的备份,在项目中点击点击Integrations出现500错误。 解决方法:1.进入新服务器,将 /etc/gitlab/gitlab-secrets.json重命名为 /etc/gitlab/gitlab-secrets.json.bak …...

【2023高教社杯】A题 定日镜场的优化设计 问题分析及数学模型
【2023高教社杯】A题 定日镜场的优化设计 问题分析及数学模型 1 题目 构建以新能源为主体的新型电力系统,是我国实现“碳达峰”“碳中和”目标的一项重要措施。塔式太阳能光热发电是一种低碳环保的新型清洁能源技术[1]。 定日镜是塔式太阳能光热发电站(…...
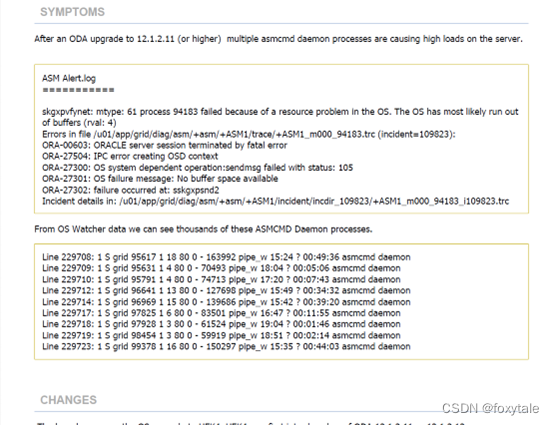
rac异常hang死故障分析(sskgxpsnd2)
x86虚拟化的平台麒麟系统的一套RAC。事件梳理20:24左右,发现一个节点hang死,关闭操作没有响应。关闭hang死节点,另一个节点也发生hang死,然后重启了另一个节点。 无效分析部分 检查gi的alert日志 有一个很大跨度的时间回退 再看…...
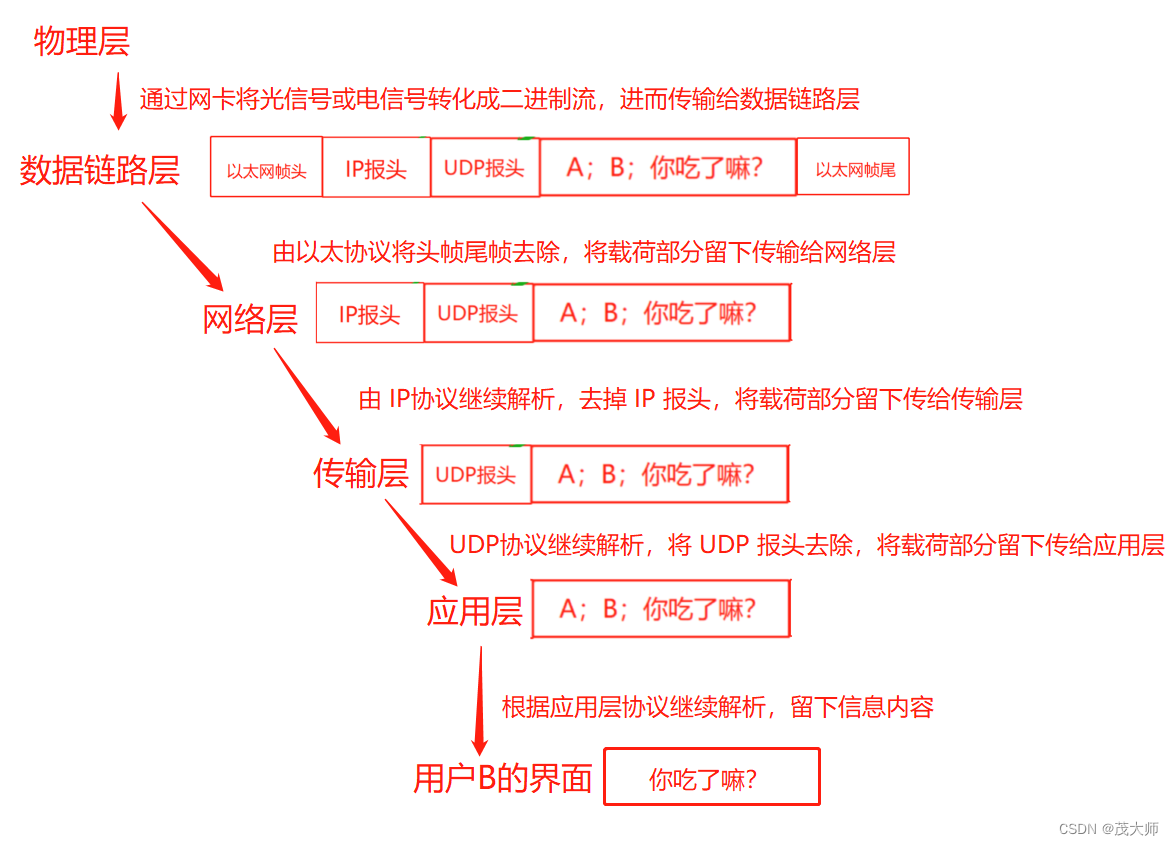
2023.9.7 关于 TCP / IP 的基本认知
目录 网络协议分层 TCP/IP 五层(四层)模型 应用层 传输层 网络层(互联网层) 数据链路层(网络接口层) 物理层 网络数据传输的基本流程 网络协议分层 为什么需要分层? 分层之后,…...

Python 图片处理
Step1 提取PDF中的图片,并另存 Step2 去除灰色纸张背景 import PyPDF2 from PIL import ImageEnhance,Image,ImageFilter import cv2 import numpy as np from skimage.filters import unsharp_mask from skimage.filters import gaussian from skimage.restora…...

信道估计 | 信道
文章目录 定义分类LS 估计MMSE估计LS vs MMSE 定义 从接收数据中将假定的某个信道模型参数估计出来的过程,如果信道是线性的,信道估计是对系统的冲击响应进行估计,需强调的是,信道估计是信道对输入信号影响的一种数学表示&#x…...

腾讯发布超千亿参数规模的混元大模型;深度学习与音乐分析与生成课程介绍
🦉 AI新闻 🚀 腾讯发布超千亿参数规模的混元大模型 摘要:腾讯在2023腾讯全球数字生态大会上发布混元大模型,该模型拥有超千亿的参数规模和超2万亿 tokens 的预训练语料。混元大模型将支持多轮对话、内容创作、逻辑推理、知识增强…...

[html]当网站搭建、维护的时候,你会放个什么界面?
效果图: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>网站建设中</title><style>/* 基础样式 */body, html {margin: 0;padding: 0;height: 100%;font-family: Arial, sa…...
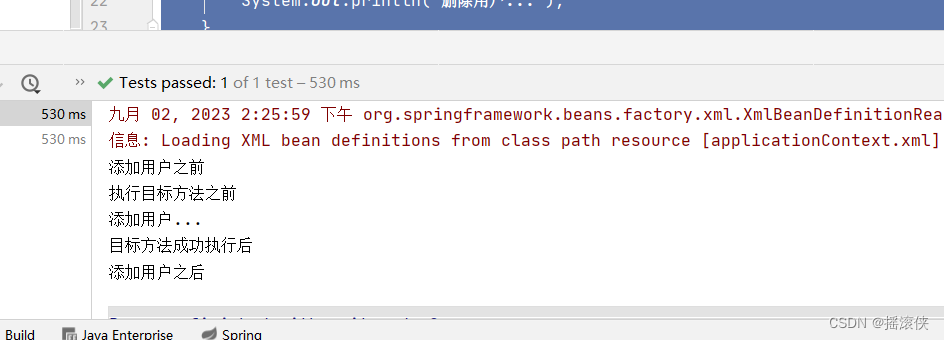
javaee spring aop 的五种通知方式
spring配置文件 <?xml version"1.0" encoding"UTF-8"?> <beans xmlns"http://www.springframework.org/schema/beans"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance" xmlns:aop"http://www.springframework.…...
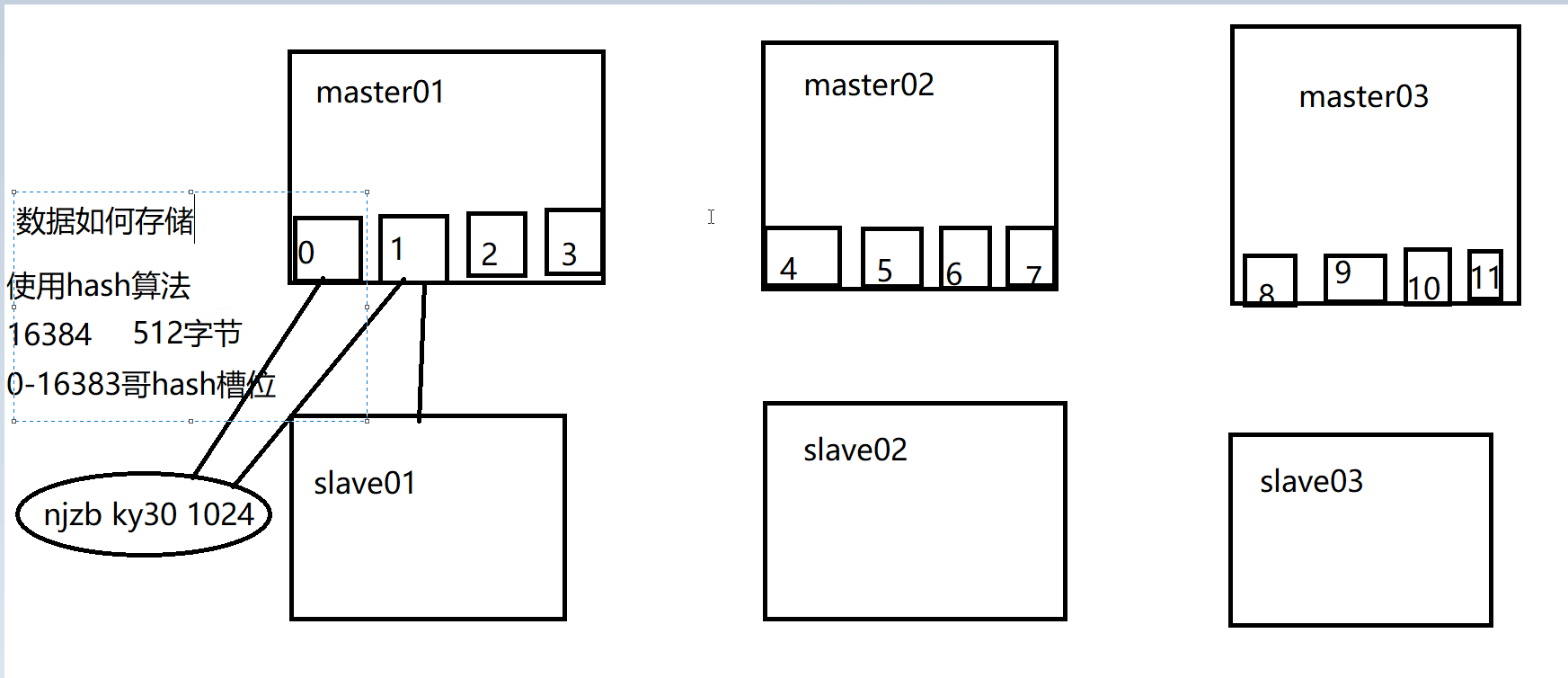
【Redis】3、Redis主从复制、哨兵、集群
Redis主从复制 主从复制,是指将一台Redis服务器的数据,复制到其他的Redis服务器。前者称为主节点(Master),后者称为从节点(Slave);数据的复制是单向的,只能由主节点到从节点。 默认情况下,每台Redis服务器…...

vcpkg方式安装zlmediakit
主要参考: https://github.com/ZLMediaKit/ZLMediaKit/wiki/vcpkg%E6%96%B9%E5%BC%8F%E5%AE%89%E8%A3%85zlmediakit vcpkg的相关配置不在本文论述。很多库或源码下载不下来,通过第三方下载后放在download目录下,名称要和vcpkg期望的一致。可通过云服务器…...

【大数据】基于 Flink CDC 高效构建入湖通道
基于 Flink CDC 高效构建入湖通道 1.Flink CDC 核心技术解析2.CDC 数据入湖入仓的挑战2.1 CDC 数据入湖架构2.2 CDC 数据 ETL 架构 3.基于 Flink CDC 的入湖入仓方案3.1 Flink CDC 入湖入仓架构3.2 Flink CDC ETL 分析3.3 存储友好的写入设计3.4 Flink CDC 实现异构数据源集成3…...

微信小程序开发---网络数据请求
目录 一、小程序中网络数据请求的限制 二、发起get请求 三、发起post请求 一、小程序中网络数据请求的限制 具体有两个限制: (1)只能请求HTTPS类型的接口 (2)必须将接口的域名添加到信任列表中,在调试的时…...

vulkan学习路径
1.学习路径 了解图形渲染基础知识: 学习计算机图形学基础概念,包括坐标系统、三角形渲染、光照模型等。可以参考经典的图形学教材,如《Real-Time Rendering》和《Computer Graphics: Principles and Practice》。了解图形API的发展历史&#…...

NIFI使用InvokeHTTP发送http请求
说明 这里介绍四种平时常用的http请求方法:GET、POST、PUT、DELETE。 在官方的介绍文档中关于InvokeHTTP处理器的描述是这么说的: An HTTP client processor which can interact with a configurable HTTP Endpoint. The destination URL and HTTP Met…...

Spire.xls+excel文件实现单据打印
报表和单据打印,通常都是使用fastreport之类的,因为有了现成的xls模板样式,如果转成fastreport那还需要花时间,是用spire.xls这个玩意简单,超好用。 一.引用 using Spire.Xls; 二.基本的操作 // 创建工作簿ÿ…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...

算法刷题-回溯
今天给大家分享的还是一道关于dfs回溯的问题,对于这类问题大家还是要多刷和总结,总体难度还是偏大。 对于回溯问题有几个关键点: 1.首先对于这类回溯可以节点可以随机选择的问题,要做mian函数中循环调用dfs(i&#x…...
