Lesson4-2:OpenCV图像特征提取与描述---Harris和Shi-Tomas算法
学习目标
- 理解Harris和Shi-Tomasi算法的原理
- 能够利用Harris和Shi-Tomasi进行角点检测
1 Harris角点检测
1.1 原理
H a r r i s Harris Harris角点检测的思想是通过图像的局部的小窗口观察图像,角点的特征是窗口沿任意方向移动都会导致图像灰度的明显变化,如下图所示:
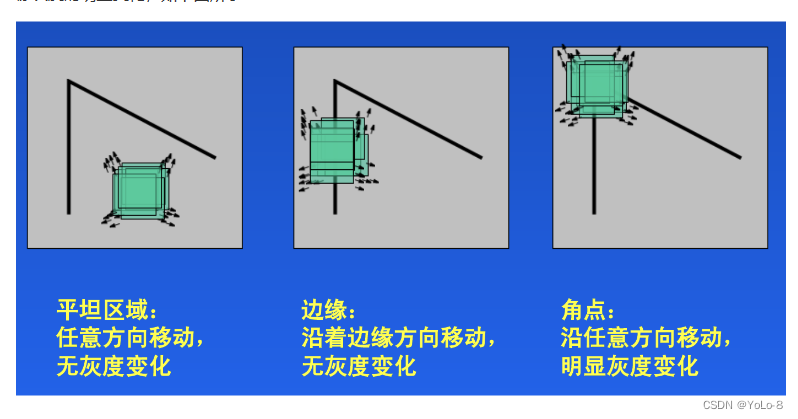
将上述思想转换为数学形式,即将局部窗口向各个方向移动 ( u , v ) (u,v) (u,v)并计算所有灰度差异的总和,表达式如下:
E ( u , v ) = ∑ x , y w ( x , y ) [ I ( x + u , y + v ) − I ( x , y ) ] 2 E(u,v)=\sum_{x,y}w(x,y)[I(x+u,y+v)-I(x,y)]^{2} E(u,v)=x,y∑w(x,y)[I(x+u,y+v)−I(x,y)]2
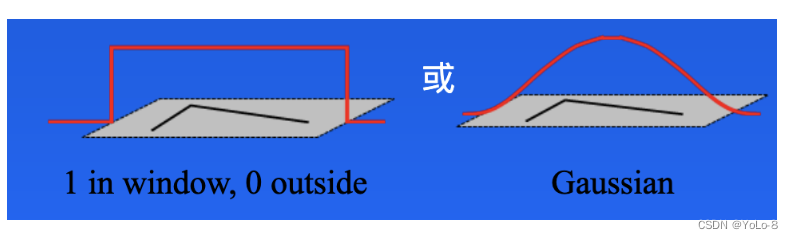
其中 I ( x , y ) I(x,y) I(x,y)是局部窗口的图像灰度, I ( x + u , y + v ) I(x+u,y+v) I(x+u,y+v)是平移后的图像灰度, w ( x , y ) w(x,y) w(x,y)是窗口函数,该可以是矩形窗口,也可以是对每一个像素赋予不同权重的高斯窗口,如下所示:
角点检测中使 E ( u , v ) E(u,v) E(u,v)的值最大。利用一阶泰勒展开有:
I ( x + u , y + v ) = I ( x , y ) + I x u + I u v I(x+u,y+v)=I(x,y)+I_{x}u+I_{u}v I(x+u,y+v)=I(x,y)+Ixu+Iuv
其中 I x I_{x} Ix和 I y I_{y} Iy是沿x和y方向的导数,可用sobel算子计算。
推导如下:
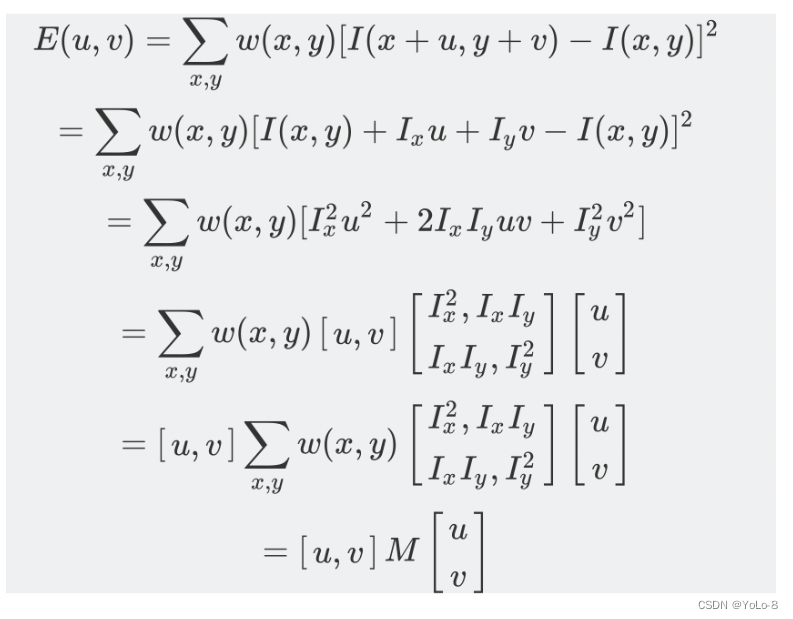
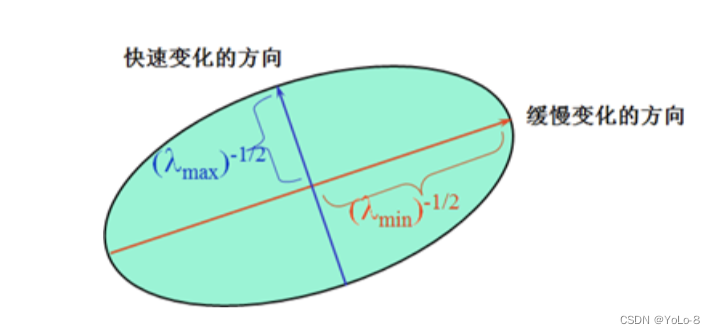
M M M矩阵决定了 E ( u , v ) E(u,v) E(u,v)的取值,下面我们利用 M M M来求角点, M M M是 I x I_{x} Ix和 I y I_{y} Iy 的二次项函数,可以表示成椭圆的形状,椭圆的长短半轴由 M M M的特征值 λ 1 λ_{1} λ1和 λ 2 λ_{2} λ2决定,方向由特征矢量决定,如下图所示:
椭圆函数特征值与图像中的角点、直线(边缘)和平面之间的关系如下图所示。
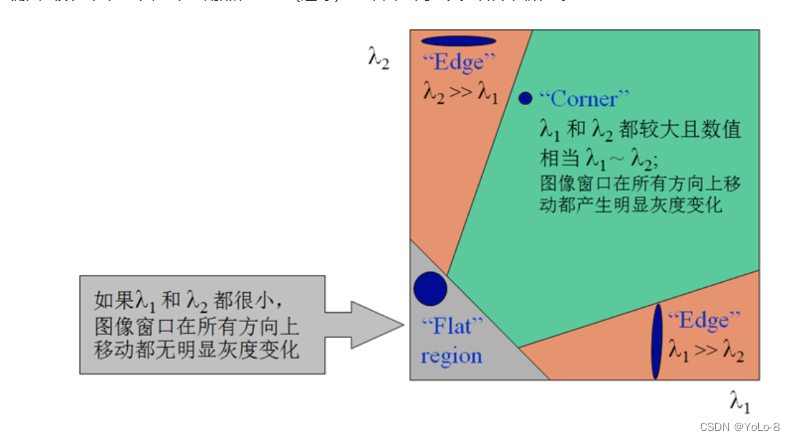
共可分为三种情况:
- 图像中的直线。一个特征值大,另一个特征值小, λ 1 > > λ 2 λ_{1}>>λ_{2} λ1>>λ2或 λ 2 > > λ 1 λ_{2}>>λ_{1} λ2>>λ1。椭圆函数值在某一方向上大,在其他方向上小。
- 图像中的平面。两个特征值都小,且近似相等;椭圆函数数值在各个方向上都小。
- 图像中的角点。两个特征值都大,且近似相等,椭圆函数在所有方向都增大
H a r r i s Harris Harris给出的角点计算方法并不需要计算具体的特征值,而是计算一个角点响应值 R R R来判断角点。
R R R的计算公式为:
R = d e t M − α ( t r a c e M ) 2 R = detM-\alpha (traceM)^{2} R=detM−α(traceM)2
式中, d e t M detM detM为矩阵 M M M的行列式; t r a c e M traceM traceM为矩阵 M M M的迹; α α α为常数,取值范围为 0.04 0.06 0.04~0.06 0.04 0.06。事实上,特征是隐含在 d e t M detM detM和 t r a c e M traceM traceM中,因为:
d e t M = λ 1 λ 2 detM=λ_{1}λ_{2} detM=λ1λ2
t r a c e M = λ 1 + λ 2 traceM=λ_{1}+λ_{2} traceM=λ1+λ2
那我们怎么判断角点呢?如下图所示:
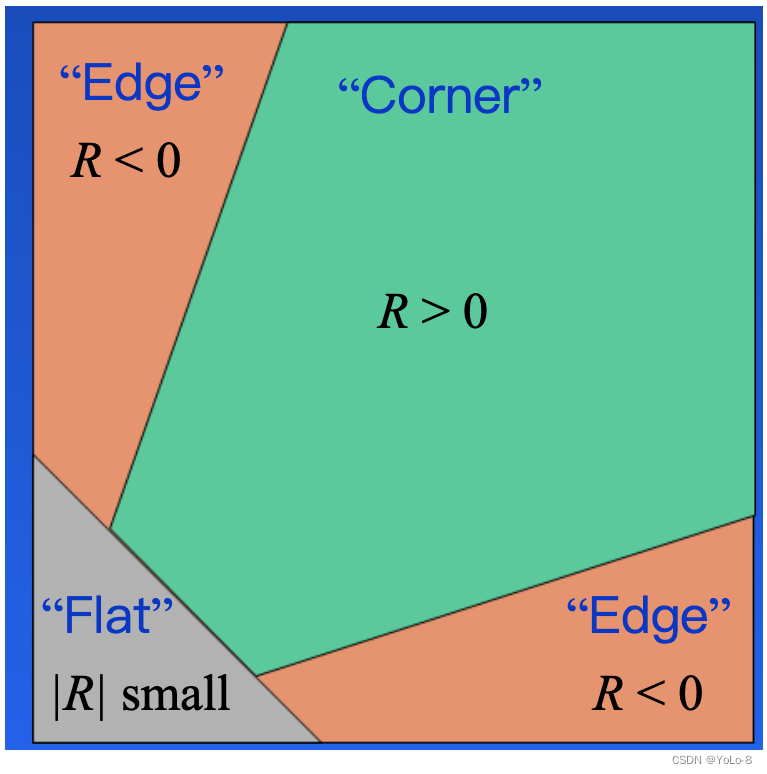
- 当 R R R为大数值的正数时是角点
- 当 R R R为大数值的负数时是边界
- 当 R R R为小数是认为是平坦区域
1.2 实现
在OpenCV中实现Hariis检测使用的API是:
dst=cv.cornerHarris(src, blockSize, ksize, k)
参数:
-
img:数据类型为 float32 的输入图像。 -
blockSize:角点检测中要考虑的邻域大小。 -
ksize:sobel求导使用的核大小 -
k:角点检测方程中的自由参数,取值参数为 [0.04,0.06].
示例:
import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
# 1 读取图像,并转换成灰度图像
img = cv.imread('./image/chessboard.jpg')
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
# 2 角点检测
# 2.1 输入图像必须是 float32
gray = np.float32(gray)# 2.2 最后一个参数在 0.04 到 0.05 之间
dst = cv.cornerHarris(gray,2,3,0.04)
# 3 设置阈值,将角点绘制出来,阈值根据图像进行选择
img[dst>0.001*dst.max()] = [0,0,255]
# 4 图像显示
plt.figure(figsize=(10,8),dpi=100)
plt.imshow(img[:,:,::-1]),plt.title('Harris角点检测')
plt.xticks([]), plt.yticks([])
plt.show()
结果如下:

Harris角点检测的优缺点:
优点:
- 旋转不变性,椭圆转过一定角度但是其形状保持不变(特征值保持不变)
- 对于图像灰度的仿射变化具有部分的不变性,由于仅仅使用了图像的一介导数,对于图像灰度平移变化不变;对于图像灰度尺度变化不变
缺点:
- 对尺度很敏感,不具备几何尺度不变性。
- 提取的角点是像素级的
2 Shi-Tomasi角点检测
2.1 原理
S h i − T o m a s i Shi-Tomasi Shi−Tomasi算法是对 H a r r i s Harris Harris角点检测算法的改进,一般会比 H a r r i s Harris Harris算法得到更好的角点。 H a r r i s Harris Harris 算法的角点响应函数是将矩阵 M M M 的行列式值与 M M M 的迹相减,利用差值判断是否为角点。后来 S h i Shi Shi 和 T o m a s i Tomasi Tomasi 提出改进的方法是,若矩阵 M M M的两个特征值中较小的一个大于阈值,则认为他是角点,即:
R = m i n ( λ 1 , λ 2 ) R=min(λ_{1} ,λ_{2}) R=min(λ1,λ2)
如下图所示:
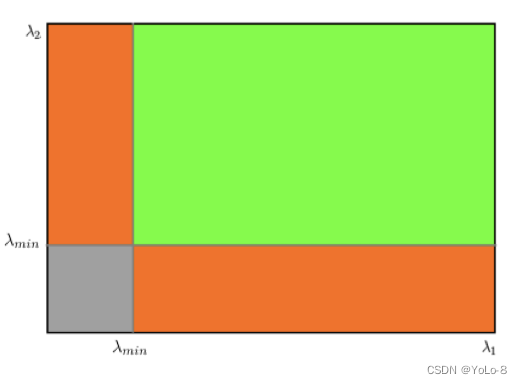
从这幅图中,可以看出来只有当 λ 1 λ_{1} λ1 和 λ 2 λ_{2} λ2 都大于最小值时,才被认为是角点。
2.2 实现
在OpenCV中实现Shi-Tomasi角点检测使用API:
corners = cv2.goodFeaturesToTrack ( image, maxcorners, qualityLevel, minDistance )
参数:
Image: 输入灰度图像maxCorners: 获取角点数的数目。qualityLevel:该参数指出最低可接受的角点质量水平,在0-1之间。minDistance:角点之间最小的欧式距离,避免得到相邻特征点。
返回:
Corners: 搜索到的角点,在这里所有低于质量水平的角点被排除掉,然后把合格的角点按质量排序,然后将质量较好的角点附近(小于最小欧式距离)的角点删掉,最后找到 m a x C o r n e r s maxCorners maxCorners个角点返回。
示例:
import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
# 1 读取图像
img = cv.imread('./image/tv.jpg')
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
# 2 角点检测
corners = cv.goodFeaturesToTrack(gray,1000,0.01,10)
# 3 绘制角点
for i in corners:x,y = i.ravel()cv.circle(img,(x,y),2,(0,0,255),-1)
# 4 图像展示
plt.figure(figsize=(10,8),dpi=100)
plt.imshow(img[:,:,::-1]),plt.title('shi-tomasi角点检测')
plt.xticks([]), plt.yticks([])
plt.show()
结果如下:

总结
-
Harris算法
思想:通过图像的局部的小窗口观察图像,角点的特征是窗口沿任意方向移动都会导致图像灰度的明显变化。
API:
cv.cornerHarris() -
Shi-Tomasi算法
对Harris算法的改进,能够更好地检测角点
API:
cv2.goodFeatureToTrack()
相关文章:

Lesson4-2:OpenCV图像特征提取与描述---Harris和Shi-Tomas算法
学习目标 理解Harris和Shi-Tomasi算法的原理能够利用Harris和Shi-Tomasi进行角点检测 1 Harris角点检测 1.1 原理 H a r r i s Harris Harris角点检测的思想是通过图像的局部的小窗口观察图像,角点的特征是窗口沿任意方向移动都会导致图像灰度的明显变化ÿ…...
华为云云耀云服务器L实例评测|部署spring项目端口开放问题的解决 服务器项目环境搭建MySQL,Redis,Minio...指南
目录 引出书接上回,部署spring项目,端口访问失败最后排查结果反馈 尝试的几种解决方案【未成功】1.指定tomcat启动ipv4端口2.添加开放端口规则保存规则防火墙相关命令记录 最终成功解决【成功!】用firewall成功了问题来了,如果这里…...
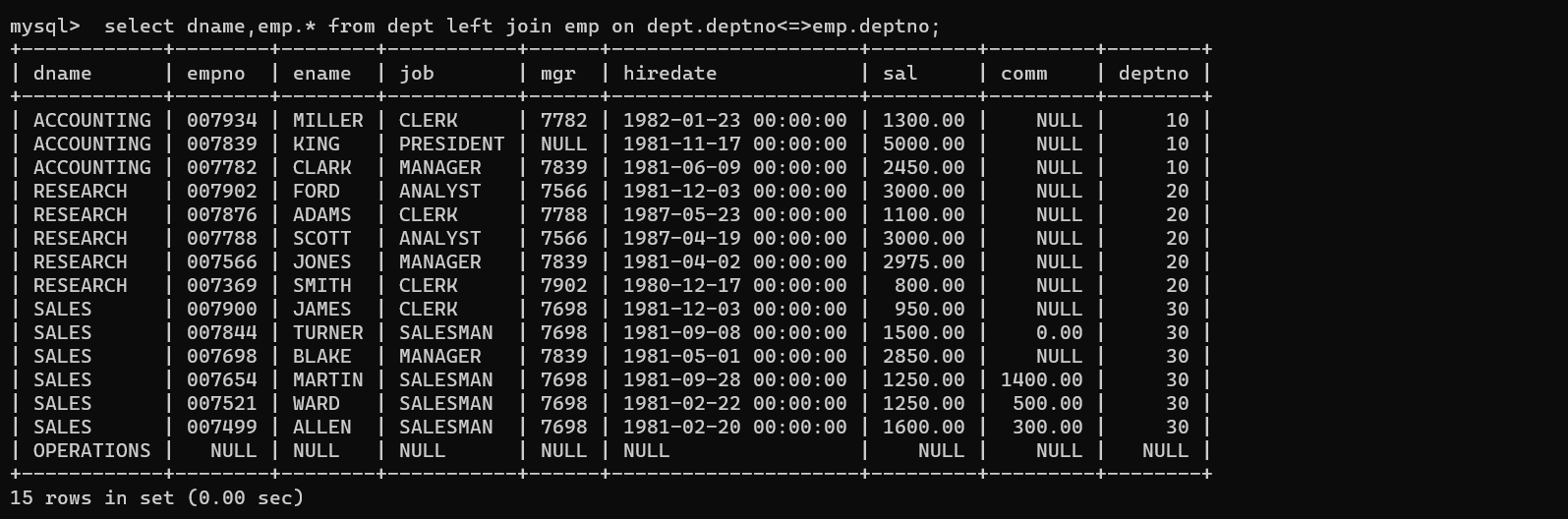
MySQL内外连接
MySQL内外链接 内连接显示SMITH的名字和部门名称 外连接左外连接查询所有学生的成绩,如果这个学生没有成绩,也要将学生的个人信息显示出来 右外连接把所有的成绩都显示出来,即使这个成绩没有学生与它对应,也要显示出来列出部门名称…...

sql:SQL优化知识点记录(十四)
(1)索引失效行锁变表锁 建立2个索引 索引是失效后,系统性能会变查,如果涉及到锁的话,行锁会变表锁 有一个问题,当session1用b字段做查询条件因为是varchar类型,需要加双引号,但是没…...

什么是IIFE(Immediately Invoked Function Expression)?它有什么作用?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐IIFE 的基本语法⭐IIFE 的主要作用⭐如何使用 IIFE 来创建私有变量和模块封装⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅…...
(A - D))
Codeforces Round 866 (Div 2)(A - D)
Codeforces Round 866 (Div. 2)(A - D) Dashboard - Codeforces Round 866 (Div. 2) - Codeforces A. Yura’s New Name(思维) 思路:枚举每个下划线 , 计算其前后需要补齐的 ‘^’ 个数 , 注意特判样例四的特殊情况…...
QTday3(QT实现文件对话框保存操作、实现键盘触发事件【WASD控制小球的移动】)
1.实现文件对话框保存操作 #include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }void Widget::on_fontBtn_clicked() {//调用QFo…...

WPF基础入门-Class8-资源基础
WPF基础入门 Class8-资源基础 前言:方便各种资源的集中管理和动态效果 静态引用:初始化的时候确定样式,后续不发生改变 动态引用:样式随着引用的内容一起改变 1、新建资源字典.xaml,创建一个边框颜色资源MyBrush和一…...
Axure RP PC电商平台Web端交互原型模板
Axure RP PC电商平台Web端交互原型模板。原型图内容齐全,包含了用户中心、会员中心、优惠券、积分、互动社区、运营推广、内容推荐、商品展示、订单流程、订单管理、售后及服务等完整的电商体系功能架构和业务流程。 在设计尺寸方面,本套模板按照主流的…...

Ubuntu目录和linux内核文件用途
一,目录: 1./:根目录,是整个文件系统的起点 2./bin:binary 二进制可执行文件目录,包含用于系统启动和运行的基本命令 3./boot: 启动加载器目录,包含用于系统启动的内核和引导程序文件。 4./dev: device 设备文件目录&a…...

更快更强更稳定:腾讯向量数据库测评
向量数据库:AI时代的新基座 人工智能在无处不在影响着我们的生活,而人工智能飞速发展的背后是需要对越来越多的海量数据处理,传统数据库已经难以支撑大规模的复杂数据处理。特别是大模型的出现,向量数据库横空出世。NVIDIA CEO黄…...

【java web】JSP-Java Server Page
前言 这个框架我用得不多,感觉和python的django一样,前后端结合太紧密了,适合个人开发 get 明文请求,可以被直接收藏 post 密文请求 JSP Java Server Page(JSP)HTMLJava code 步骤: 1.…...

java文件命令行报错: 找不到或无法加载主类XXX报错及解决
前言 之前遇到过几次,后面稀里糊涂的解决了。今天详细记录一下,可能不全或有些错误,还请各位指正。 你要启动一个类的话首先要有类。 在这里,类有两种, 一个是带包名(package)的还有一个是没包…...

算法训练营day46|动态规划 part08:完全背包 (LeetCode 139. 单词拆分)
139. 单词拆分 (求排列方法) 题目链接🔥🔥 给定一个非空字符串 s 和一个包含非空单词的列表 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。 说明: 拆分时可以重复使用字典中的单词。 你可以假设字典中没…...
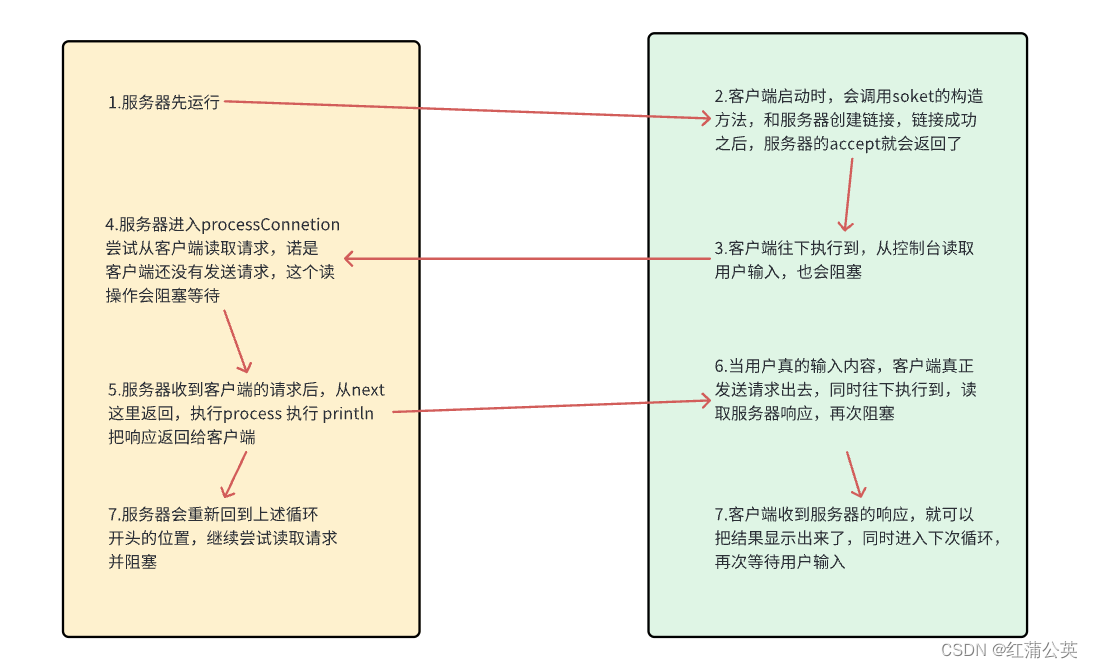
Java网络编程(二)Socket 套接字(TCP和UDP),以及TCP的回显
Socket 套接字(TCP和UDP),以及TCP的回显 Socket 套接字数据报套接字UDPTCP流套接字编程TCP的长短连接实现一个简单回显服务器 Socket 套接字 我们软件工作者,着重编写的是应用层的代码,但是发送这个数据,我…...
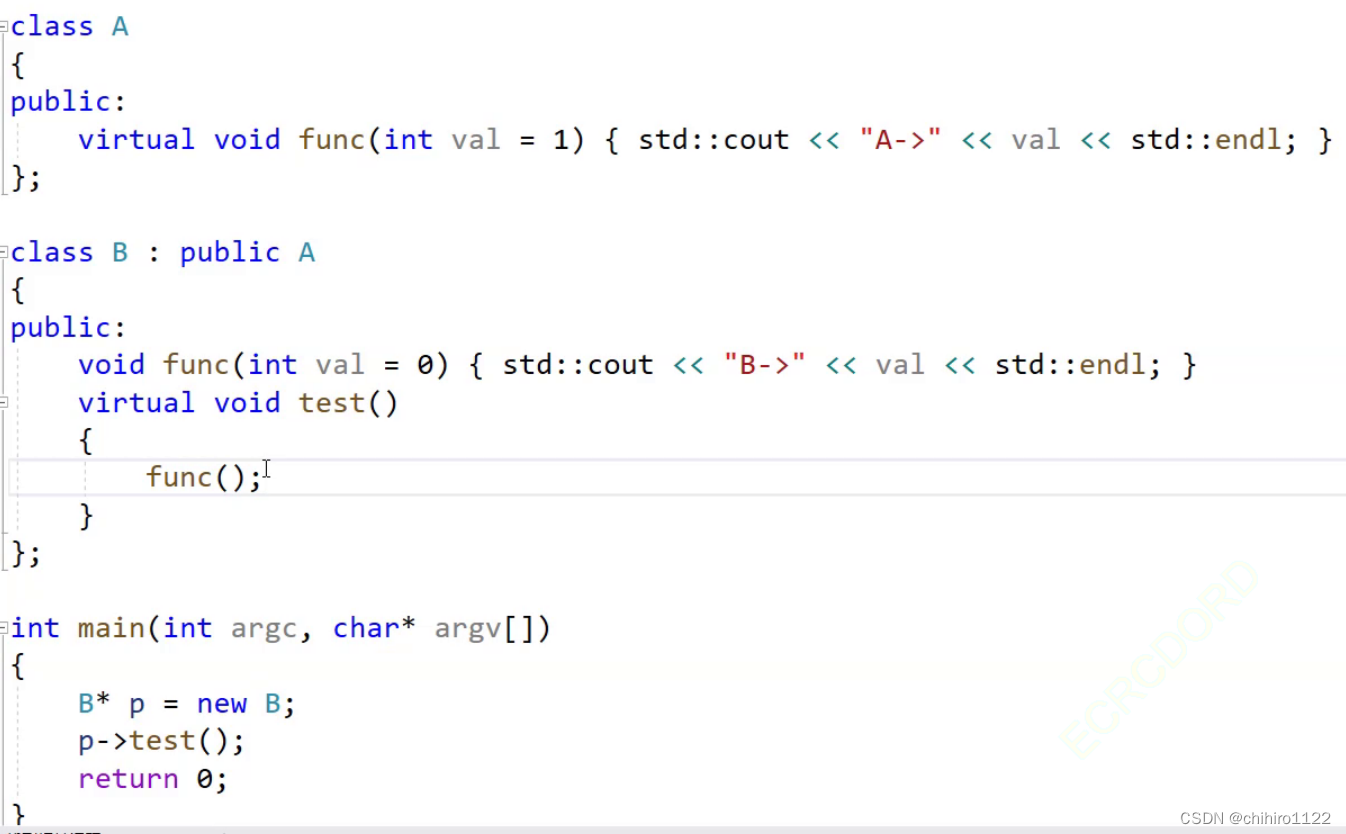
C++ - 多态语法 - 虚函数使用介绍
多态简单介绍 多态就是多种形态,是不同的对象去完成同一个动作所产生的结果可能有多种。这种多种的形态我们称之为多态。 比如:我们在买票的时候的时候,可能有成人全价,儿童半价,军人免票等等。对于成人,儿…...

php获取客户端ip地址及ip所在国家、省份、城市、县区
摘要 获取客户端ip地址,然后使用这个ip地址获取所在的国家、省份、城市,可以在网站中实现IP属地,发布地等功能。 本文的获取IP地址信息均采自网络上免费的IP查询网站,通过其API或者网页HTML解析出的ip地址信息。 代码 <?p…...

Error: Port Library failed to initialize: -86
最近遇到一个很奇怪的错误,这里记录一下,以备以后再次遇到 Error: Port Library failed to initialize: -86 Error: Could not create the Java Virtual Machine. Error: A fatal exception has occurred. Program will exit.背景是,就是一普…...

SOME/IP 支持两种序列化方式:TLV 和 TV
SOME/IP 是一种基于 IP 的可扩展面向服务的中间件协议,它可以在车载以太网中实现 ECU 之间的高效通信和互操作性。 SOME/IP 的序列化方式是指将数据结构或对象按照一定的规则转换成字节序列的过程,以便在网络中传输和解析。 SOME/IP 支持两种序列化方式:TLV 和 TV。 TLV是…...
Unity之3D物理导航系统
一 介绍 Unity自带寻路(导航)系统是unity官方自带的一种寻路系统。我们可以通过它来制作简单的寻路,比如可以制作点击某个位置,让角色自动的绕开障碍走到目标点的效果,比如可以制作敌人AI,让它可以通过NavMesh绕开障碍追击我方单…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
未授权访问事件频发,我们应当如何应对?
在当下,数据已成为企业和组织的核心资产,是推动业务发展、决策制定以及创新的关键驱动力。然而,未授权访问这一隐匿的安全威胁,正如同高悬的达摩克利斯之剑,时刻威胁着数据的安全,一旦触发,便可…...
