C++之红黑树
红黑树
- 红黑树的概念
- 红黑树的性质
- 红黑树结点的定义
- 红黑树的插入
- 红黑树的验证
- 红黑树与AVL树的比较
红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
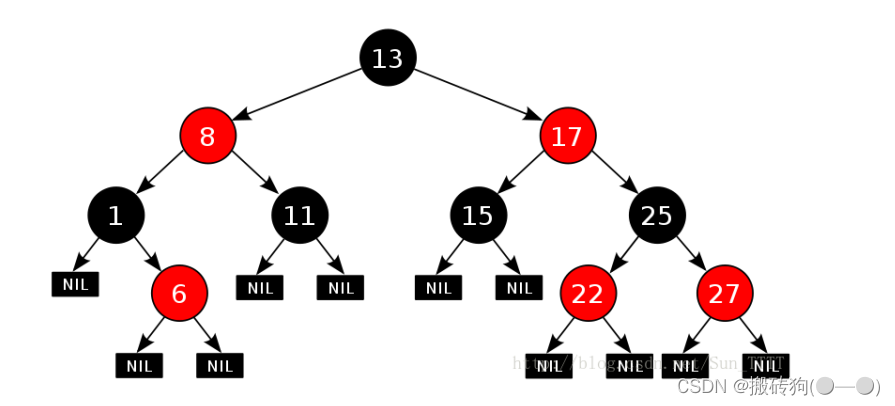
红黑树的性质
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
为什么红黑树就能保证其最长路径中节点个数不会超过最短路径节点个数的两倍?
从性质3,4可以得出,一棵红黑树的最短可能路径就是全为黑结点,即为N:
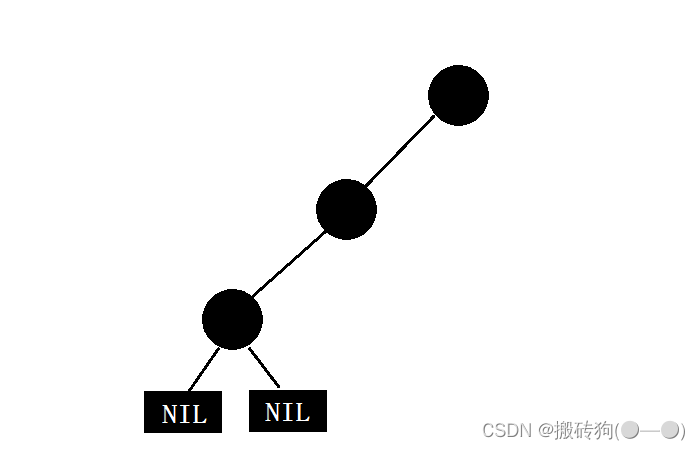
而最长可能路径就是由一黑一红结点构成的路径,该路径当中黑色结点与红色结点的数目相同,即长度为2N ;
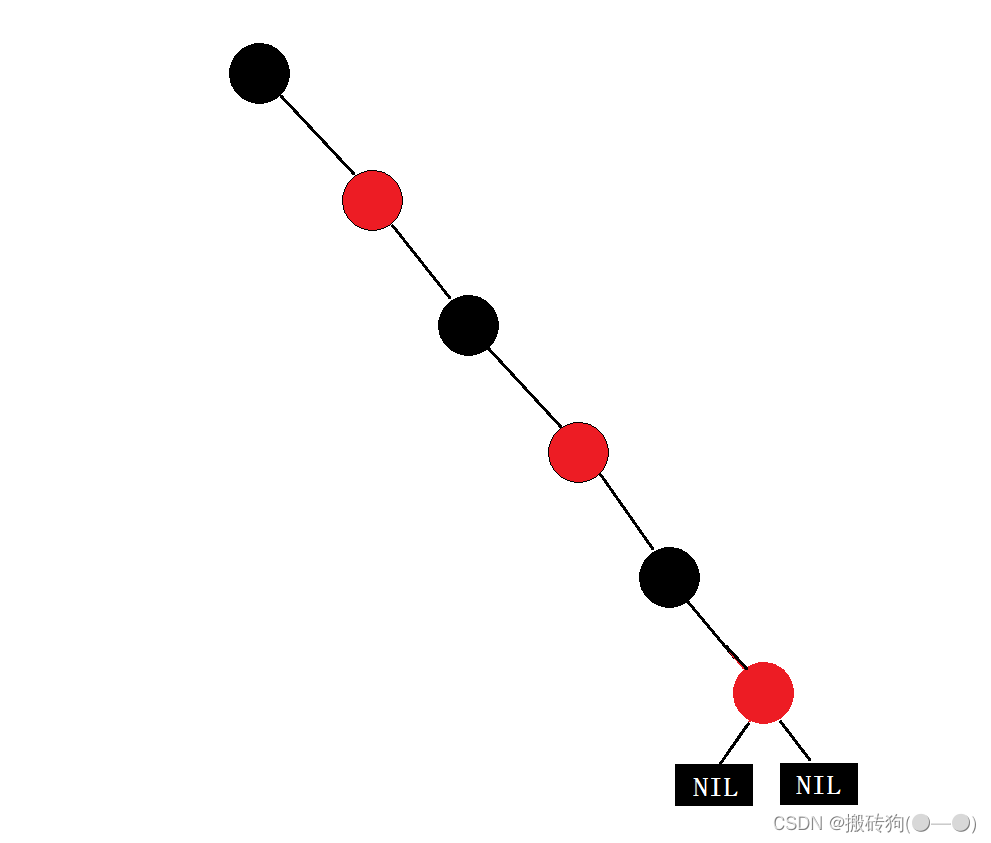
红黑树结点的定义
红黑树结点的定义其实和AVL树差不多,只不过红黑树结点少了平衡因子,多了颜色。
//枚举结点颜色
enum color
{RED,BLACK
};
template <class K, class V>
struct RBTreeNode
{//三叉链结构RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;//存储的键值对pair<K, V> _kv;//结点颜色color _col;//构造函数RBTreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED){}
};
为什么构造结点时,默认将结点的颜色设置为红色?
我们可以发现,红黑树的有一条性质是所有路径黑色结点的数目都相等,如果欧姆尼新插入的结点默认为黑色,就会破坏这条性质,我们就需要对红黑树进行调整。
如果我们插入的是红结点,此时如果父结点是红结点,我们就需要进行调整,如果父结点是黑结点,我们就不需要进行调整。
红黑树的插入
红黑树的插入步骤分为以下三步:
- 根据二叉搜索树的性质,找到待插入位置;
- 在待插入位置插入新结点;
- 如果父结点为红色,就进行调整。
我们可以发现,前两步其实AVL树没有区别,我们只要在第三步进行调整就可以了。
那么,怎么对红黑树插入结点进行调整呢?
如果我们插入结点的父结点是黑色的,我们就不需要进行任何调整,因为这并没有破坏红黑树的性质;如果我们插入结点的父结点是红结点,我们就需要对红黑树进行调整了。
插入结点的父结点为红色,就说明祖父结点一定存在且为黑色,对红黑树的调整主要是对叔叔结点的调整。
红黑树的调整一共分为三种方式:
1.cur为红,p为红,g为黑,u存在且为红
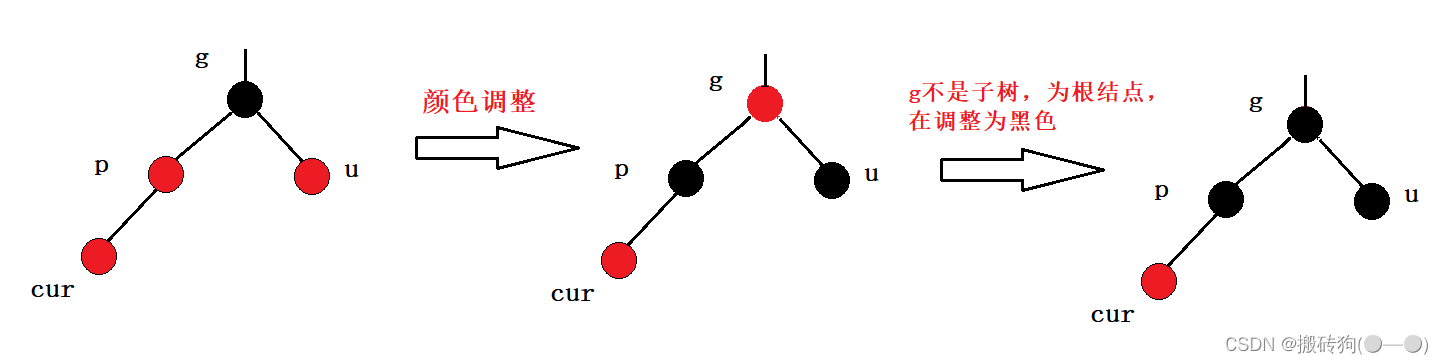
插入结点为红,父结点为红,我们需要将父结点与叔叔结点都调整为黑色,然后将祖父结点调整为红色,如果此时g这棵树不为子树,就再将祖父结点调整为黑色;
对应的抽象图如下:
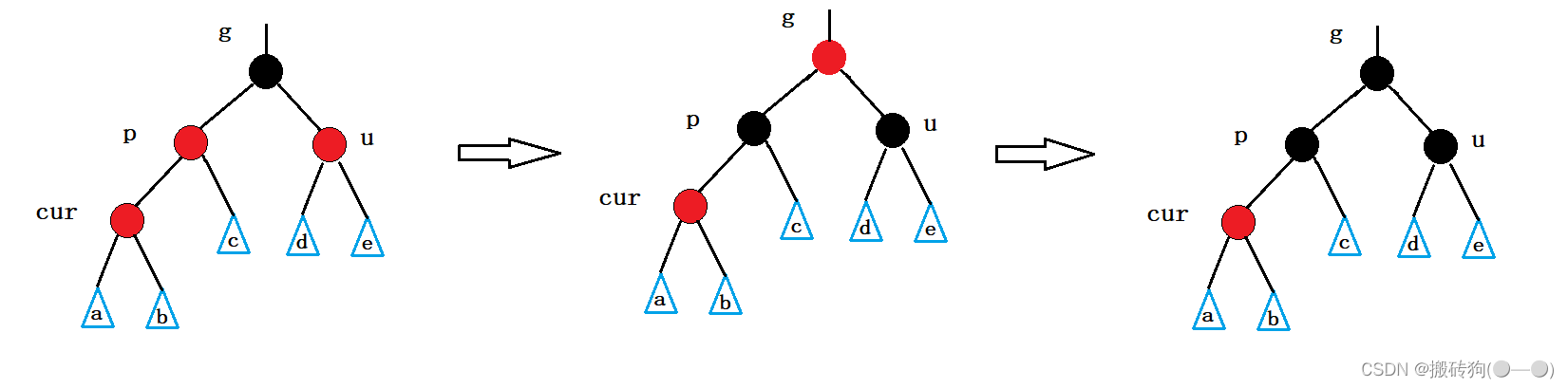
如果g不为子树,最后将g调整为黑色就完成了红黑树的调整;
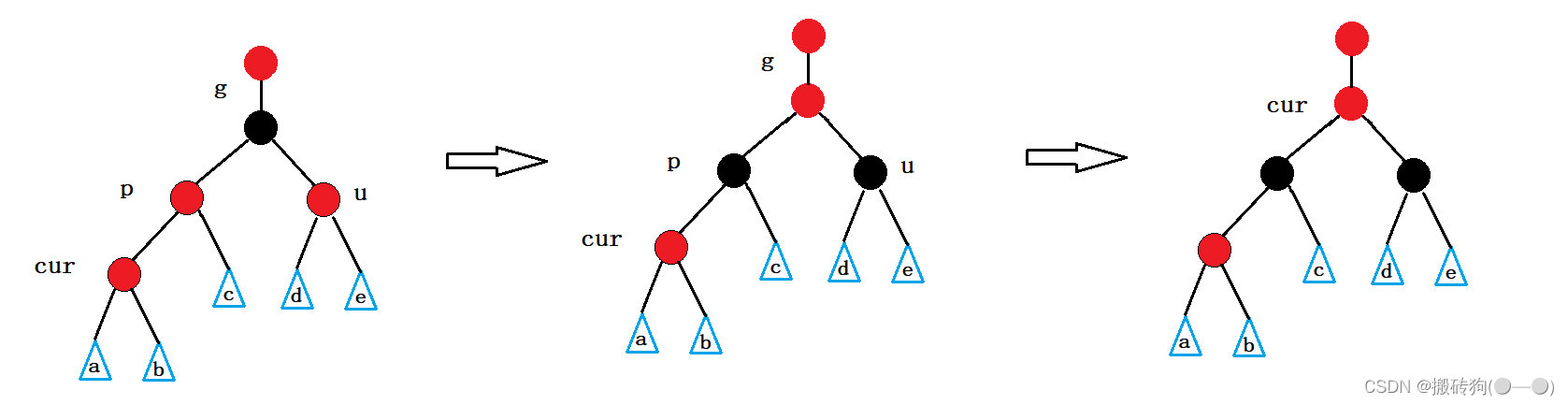
如果g为子树,一次调整以后g还有双亲,双亲如果是红色,将p,u改为黑,g改为红,然后把g当成cur,继续向上调整,还要继续向上调整。
2.cur为红,p为红,g为黑,u不存在/u存在且为黑,p为g的左孩子,cur为p的左孩子或者p为g的右孩子,cur为g的右孩子
我们均已被插入结点在根结点左侧为例:
如果u节点不存在,则cur一定是新插入节点,因为如果cur不是新插入节点则cur和p一定有一个节点的颜色是黑色,就不满足性质:每条路径黑色节点个数相同。
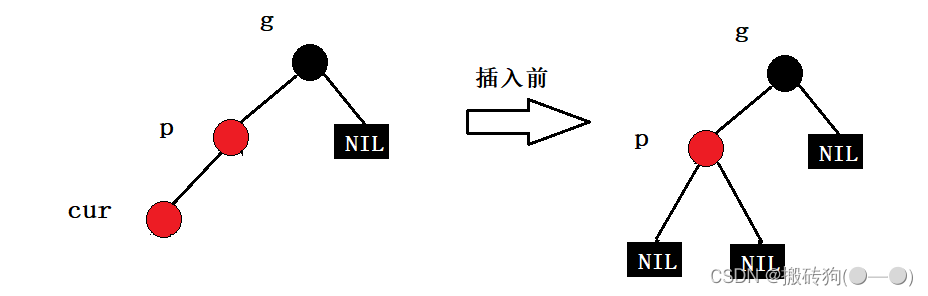
此时我们只需要以p为旋转点进行右单旋,然后进行颜色调整即可:
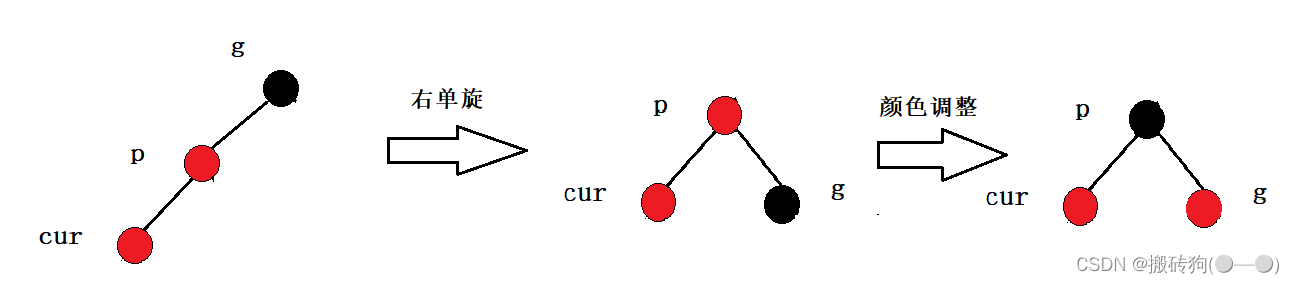
当u存在且为黑时:
此时一定是情况一向上调整才会出现的情况,这种情况下cur不会是新插入的结点,是经过前一次调整以后的结点:
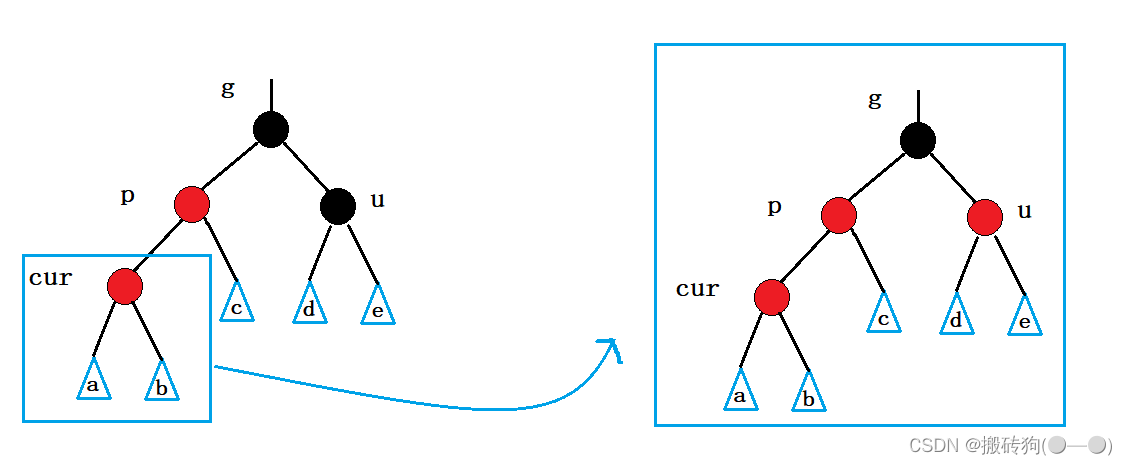
我们以新插入结点在a的左侧为例:
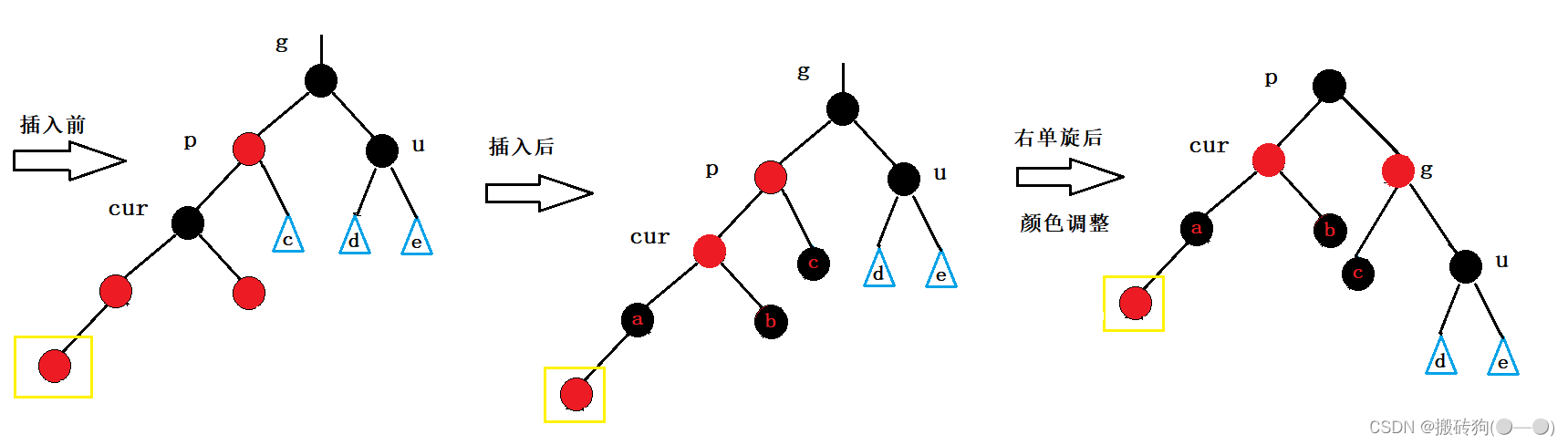
此时我们以g为旋转点进行右单旋,然后进行颜色调整,红黑树即可平衡;
同样,如果被插入结点在根结点右侧,我们只需要进行相应左旋在调整颜色即可实现红黑树平衡;
抽象图如下:
被插入结点在根结点左侧:
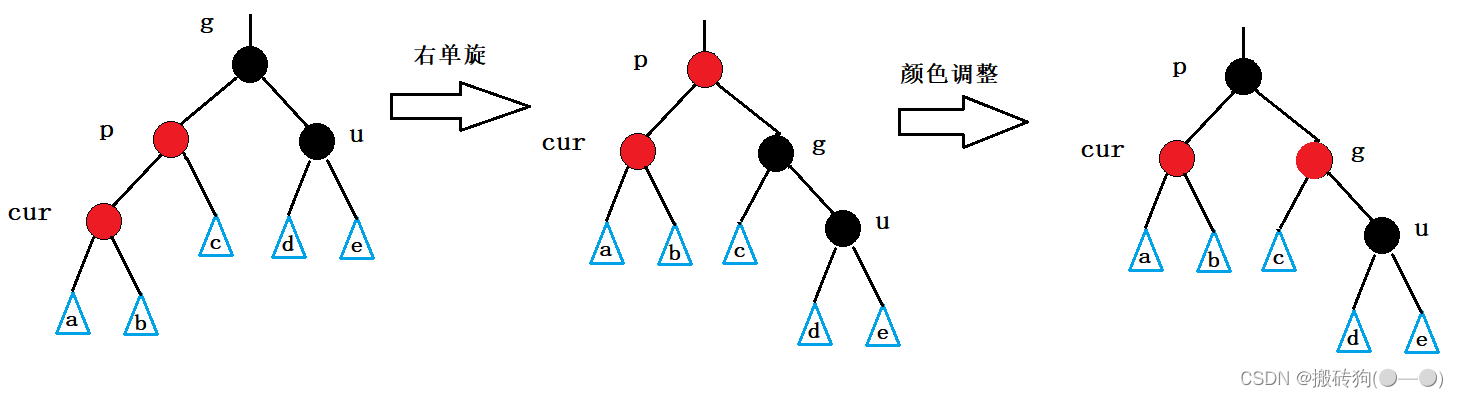
被插入结点在根结点右侧:
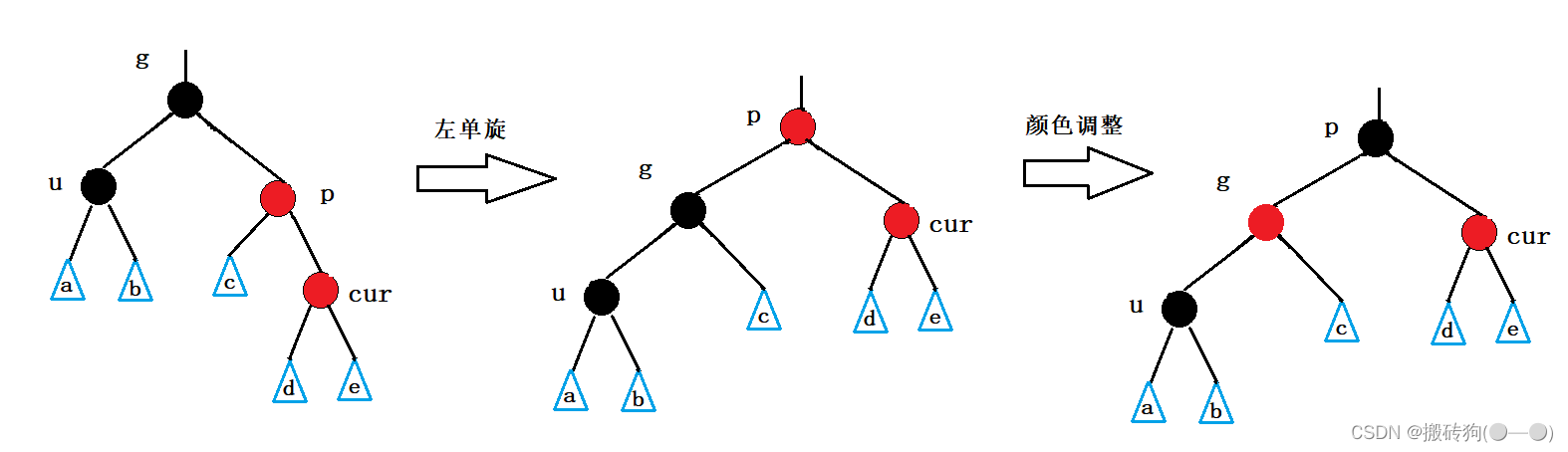
3.cur为红,p为红,g为黑,u不存在/u存在且为黑,p为g的左孩子,cur为p的右孩子或者p为g的右孩子,cur为p的左孩子
u不存在时:

当u存在且为黑时,我们以下面这种情况为例:
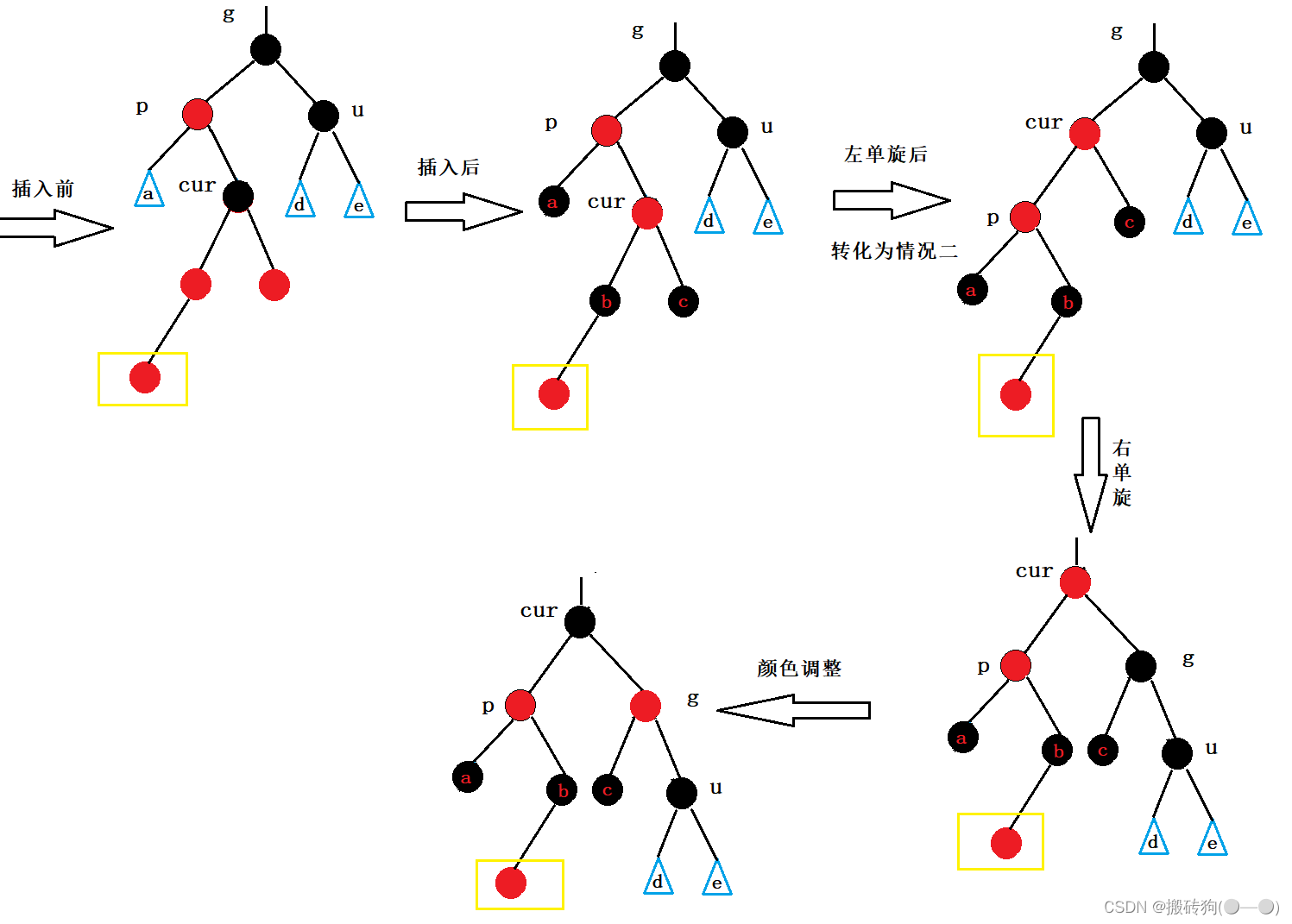
我们先已p为轴点进行左单旋,再以g为轴点进行右单旋,最后进行颜色调整,红黑树保持平衡;
抽象图如下:
被插入结点在根结点左侧:
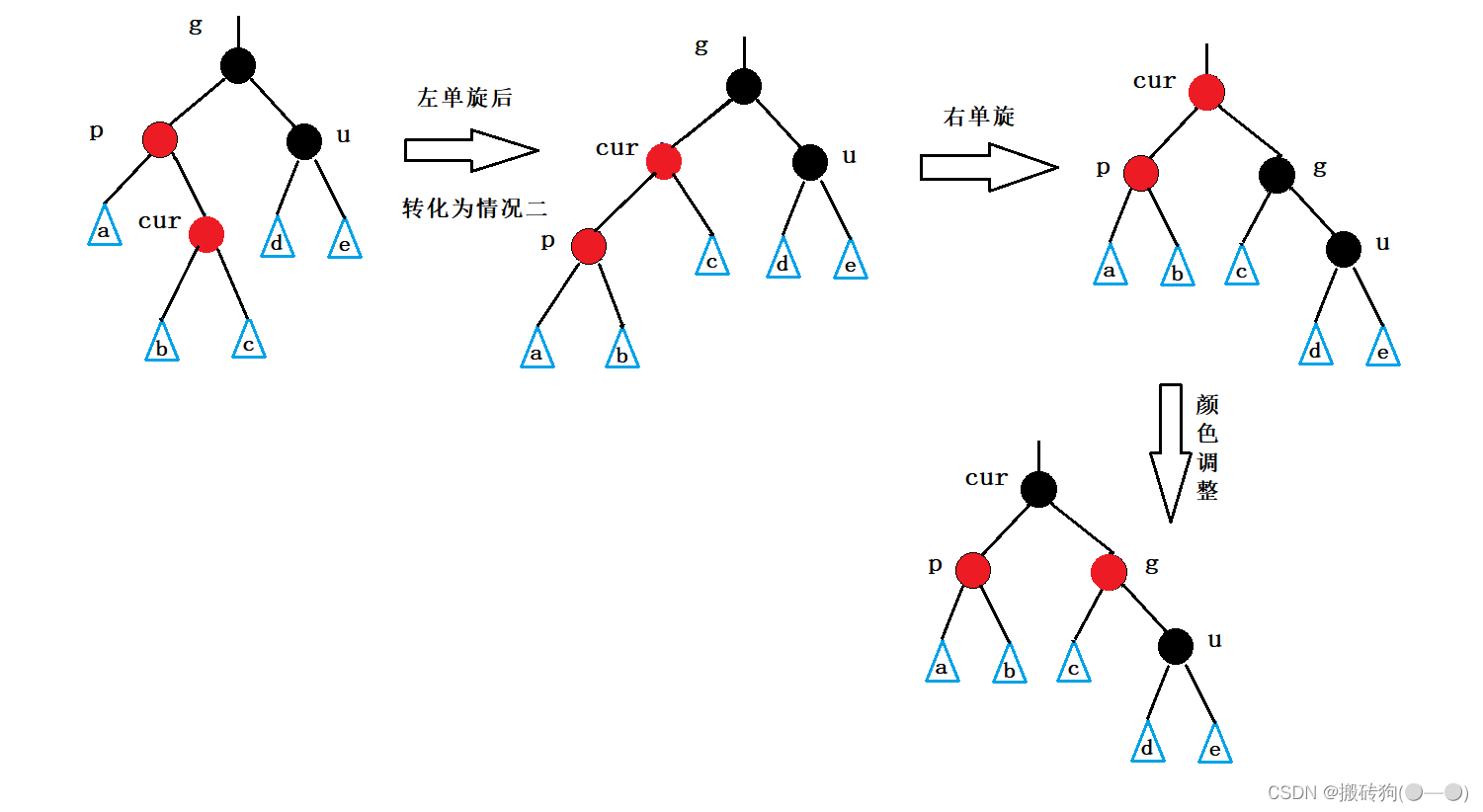
被插入结点在根结点右侧:
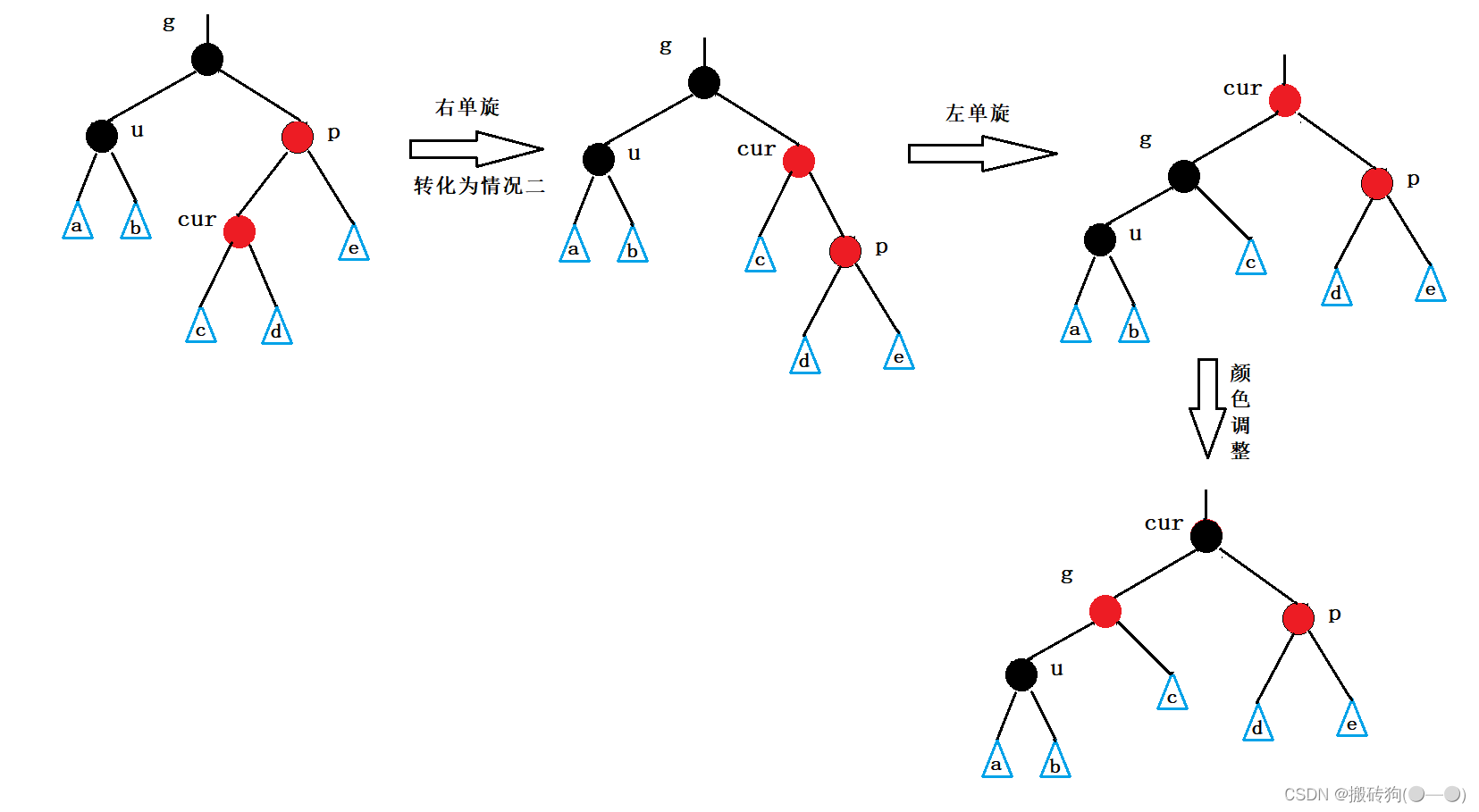
代码实现:
bool Insert(const pair<K, V>& kv)
{//根结点为空if (_root == nullptr){//创建根结点_root = new Node(kv);//颜色变为黑_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while (cur){//如果插入key值小于根结点key值if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}//如果插入key值大于根结点key值else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}//相等,返回falseelse{return false;}}//创建cur结点cur = new Node(kv);//颜色初始化为红色cur->_col = RED;//如果插入key值小于parent结点key值if (parent->_kv.first > kv.first){//在左边插入parent->_left = cur;}//如果插入key值大于parent结点key值else{//在右边插入parent->_right = cur;}//跟父结点连接起来cur->_parent = parent;while (parent && parent->_col == RED){//定义祖父节点Node* grandfather = parent->_parent;assert(grandfather);assert(grandfather->_col == BLACK);//如果父结点在祖父节点左边if (parent == grandfather->_left){//定义叔叔结点在祖父结点右边Node* uncle = grandfather->_right;//情况一://叔叔结点存在且为红if (uncle && uncle->_col == RED){//进行颜色调整parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续向上调整cur = grandfather;parent = cur->_parent;}//情况二和三://叔叔结点不存在或者存在且为黑else{//插入结点在父结点左边if (cur == parent->_left){//右单旋+颜色调整RotateR(grandfather);grandfather->_col = RED;parent->_col = BLACK;}//插入结点在父结点左边else{//左右双旋+颜色调整RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}//如果父结点在祖父节点右边else{//定义叔叔结点在祖父结点左边Node* uncle = grandfather->_left;//情况一://叔叔结点存在且为红if (uncle && uncle->_col == RED){//颜色调整parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//向上调整cur = grandfather;parent = cur->_parent;}//情况二和三://叔叔结点不存在或者存在且为黑else{//插入结点在父结点右边if (cur == parent->_right){//左单旋+颜色调整RotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}//插入结点在父结点左边else{//右左双旋+颜色调整RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}//根结点变为黑色_root->_col = BLACK;return true;
}
红黑树的验证
我们可以判断每条路径的黑节点数量是否相等来判断该二叉树是否为红黑树:
void InOrder()
{_InOrder(_root);cout << endl;
}bool IsBalance()
{//如果根结点为空,返回true;if (_root == nullptr){return true;}//如果根结点为红色,则返回false;if (_root->_col == RED){cout << "根结点不是黑色" << endl;return false;}//定义一个黑色结点数量的基准值,为最左边路径黑色结点数量int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){benchmark++;}cur = cur->_left;}//黑色结点数量int BlackNum = 0;return PrevCheck(_root, BlackNum, benchmark);
}
bool PrevCheck(Node* root, int BlackNum, int benchmark)
{//说明此时路径已经走完了if (root == nullptr){//如果基准值不等于黑色结点数量,返回falseif (benchmark != BlackNum){cout << " 某条黑色结点数量不相等" << endl;return false;}//否则返回truereturn true;}//根结点为黑色,黑色结点数量++if (root->_col == BLACK){BlackNum++;}//存在连续红色节点,返回falseif (root->_col == RED && root->_parent->_col == RED){cout << "存在连续的红色结点" << endl;return false;}//递归进行判断return PrevCheck(root->_left, BlackNum, benchmark)&& PrevCheck(root->_right, BlackNum, benchmark);
}
红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O(log N),红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单。
相关文章:

C++之红黑树
红黑树 红黑树的概念红黑树的性质红黑树结点的定义红黑树的插入红黑树的验证红黑树与AVL树的比较 红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上…...
TCP)
Go语言网络编程(socket编程)TCP
1、TCP编程 1.1.1 Go语言实现TCP通信 TCP协议 TCP/IP(Transmission Control Protocol/Internet Protocol) 即传输控制协议/网间协议,是一种面向连接(连接导向)的、可靠的、基于字节流的传输层(Transport layer)通信协…...

C语言——局部和全局变量
局部变量 定义在函数内部的变量称为局部变量(Local Variable) 局部变量的作用域(作用范围)仅限于函数内部, 离开该函数后是无效的 离开该函数后,局部变量自动释放 示例代码: #include <stdio.h>// 函数定义 …...
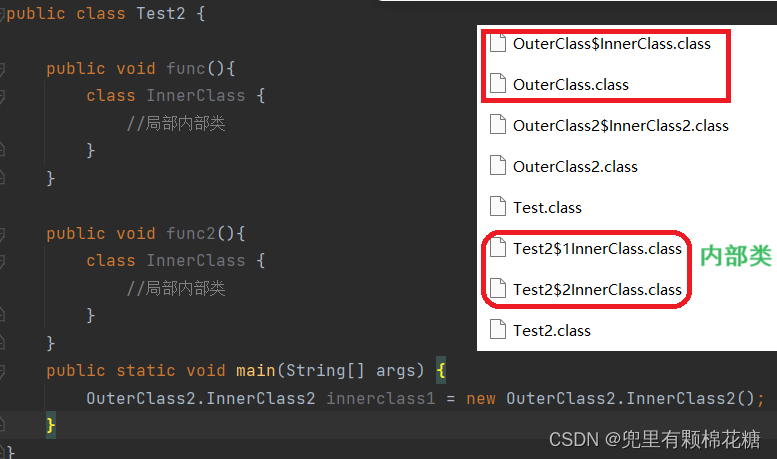
【Java基础篇 | 类和对象】--- 聊聊什么是内部类
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【JavaSE_primary】 本专栏旨在分享学习Java的一点学习心得,欢迎大家在评论区讨论💌 前言 当一个事物的内部&…...

合宙Air724UG LuatOS-Air LVGL API控件-页面 (Page)
页面 (Page) 当控件内容过多,无法在屏幕内完整显示时,可让其在 页面 内显示。 示例代码 page lvgl.page_create(lvgl.scr_act(), nil) lvgl.obj_set_size(page, 150, 200) lvgl.obj_align(page, nil, lvgl.ALIGN_CENTER, 0, 0)label lvgl.label_crea…...
mongodb数据库操作
1、启动mongodb /usr/local/mongodb/bin/mongod --dbpath /var/mongodb/data/--logpath /var/mongodb/logs/log.log &在mongodb启动命令中 --dbpath 指定mongodb的数据存储路径 --logpath 指定mongodb的日志存储路径 2、停止mongodb 第一步先进入mongo命令行模式 第二…...
第 2 章 线性表 ( 双链循环线性表(链式存储结构)实现)
1. 背景说明 2. 示例代码 1) status.h /* DataStructure 预定义常量和类型头文件 */#ifndef STATUS_H #define STATUS_H#define CHECK_NULL(pointer) if (!(pointer)) { \printf("FuncName: %-15s Line: %-5d ErrorCode: %-3d\n", __func__, __LINE__, ERR_NULL_PTR…...

redis在日常开发工作中的常见用法
redis是一款内存型数据库,在开发工作中经常用到,功能强大; 特别开一篇文章用来记录一下它的常见用法,算是一种总结; 它最主要的特点就是高可用的,速度快,分布式;有人说速度快&…...

小程序实现下拉刷新
小程序实现下拉刷新可以通过使用组件scroll-view和事件onPullDownRefresh来实现。 scroll-view组件的使用 在需要下拉刷新的页面的wxml文件中,通过scroll-view组件包裹需要滚动的内容,设置scroll-y属性为true,表示允许竖向滚动。示例代码如…...

Day 36 贪心算法 part05 : 435. 无重叠区间 763.划分字母区间 56. 合并区间
56. 合并区间 以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。 示例 1: 输入:inte…...

使用Python将网页数据保存到NoSQL数据库的方法和示例
随着大数据和人工智能技术的快速发展,对于大规模数据的处理需求日益增多。NoSQL数据库作为一种新兴的数据存储解决方案,具有高可扩展性、高性能和灵活性数据模型等优势,已经在许多行业得到广泛应用。传统的关系型数据库在处理海量数据时可能会…...

两个路由器如何连接设置的方法攻略
一、前言 随着智能家居时代来临,家里的网络部署需求开始复杂起来。往往一个路由器已经不能满足需求或者不利于拓展。两个路由器连接最常见的情况是家中已有一个路由器,并且已经通过这个路由器来正常上网。现在是因某些原因想在不改变已经在用的路由器的设…...
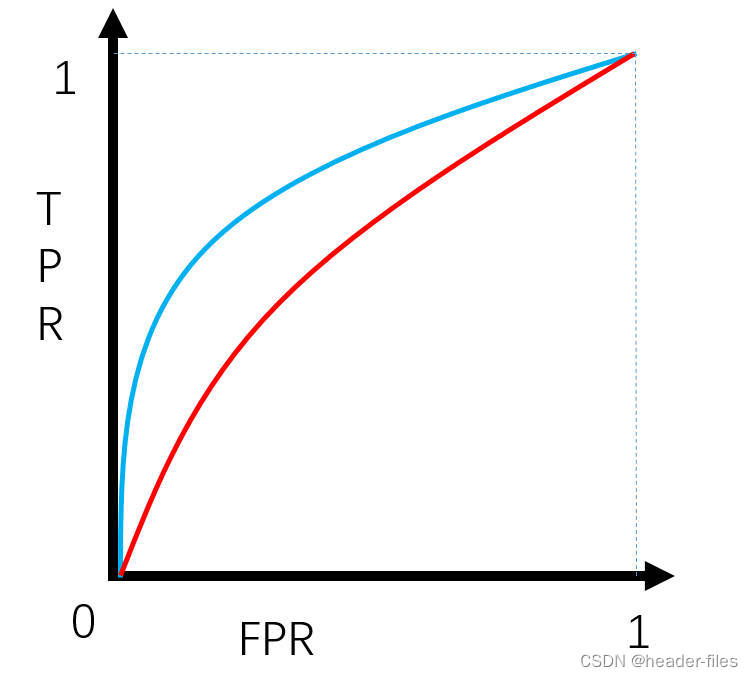
分类任务评价指标
分类任务评价指标 分类任务中,有以下几个常用指标: 混淆矩阵准确率(Accuracy)精确率(查准率,Precision)召回率(查全率,Recall)F-scorePR曲线ROC曲线 1. 混…...

c++静态成员
目录 静态成员 静态成员变量 静态成员函数 const 静态成员属性 静态成员实现单例模式 静态成员 在类定义中,它的成员(包括成员变量和成员函数),这些成员可以用关键字 static 声明为静态的,称为静态成员。 不管这…...
go-zero直连与etcd服务注册中心
go-zero中直连方式 在使用grpc是最重要的就是pb文件了,生成的pb文件,通过pb文件可以生成grpc的客户端和服务端,那么客户端和服务端就可以直连了,再次基础上可以引入etcd实现服务注册。 所有的代码都需要开发者编写,包…...
Kotlin File writeText appendText appendBytes readBytes readText
Kotlin File writeText appendText appendBytes readBytes readText import java.io.Filefun main(args: Array<String>) {val filePath "./myfile.txt"val file File(filePath)file.writeText("hello,") //如果原有文件有内容,将完全覆…...
常见缺少msvcp140.dll问题及解决方法,分享多种方法帮你解决
在日常使用电脑的过程中,我们可能会遇到各种问题,比如电脑提示msvcp140.dll文件丢失。这个问题通常是由于某些程序或游戏需要这个dll文件来正常运行,但是由于某种原因,这个文件被误删或者损坏了。那么,如何解决这个问题…...
【K210+ESP8266图传上位机开发】TCP server + JPEG图像解析上位机开发
本文章主要记录基于 【K210-ESP8266】 图传和显示的过程,上位机开发过程,系统架构和下位机开发请参考文章: 【K210-ESP8266】开发板上传图像数据到服务器并实时显示 💖 作者简介:大家好,我是喜欢记录零碎知…...

Linux查看当前文件夹的大小
在Linux中,可以使用du(disk usage)命令来查看当前文件夹的大小。以下是一些使用du的方法: 查看当前文件夹的大小: 为了查看当前文件夹的总大小,可以在文件夹中运行: du -sh .这里: -…...

YOLO目标检测——密集人群人头数据集+已标注yolo格式标签下载分享
实际项目应用:城市安防、交通管理、社会研究、商业应用、等多个领域数据集说明:YOLO密集人群人头目标检测数据集,真实场景的高质量图片数据,数据场景丰富,图片格式为jpg,共4300张图片。标注说明:…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...
