Greenplum 查找数据目录占用最大的表
背景
社区中某同学提出问题:
某环境磁盘占用空间较大,于是想找到数据目录占用最大的表。使用常规查询找不出来,于是到数据目录下分析filenode,找到3个filenode占了400G。然而根据filenode从pg_class中确找不到对应的relfilenode。
查询方法为:
select oid,relname,relfilenode from pg_class where relfilenode=...
分析
PostgreSQL中的表会有一个RelFileNode值指定这个表在磁盘上的文件名(外部表、分区表除外)。一般情况下在pg_class表的relfilenode字段可以查出这个值,但是有一些特定表在relfilenode字段的查询结果是0,如某些系统表。
另外,对于普通表,将对表执行truncate,vacuum full等操作后,会重写这个表的数据,也会引发这个表relfilenode值的变更。
具体可以参考文章https://blog.csdn.net/weixin_46199817/article/details/113108402 中的描述。
这意味着,某个对象的Oid和RelFileNode可能并不能完全对应起来,所以,当在磁盘目录中找到一个filenode,但从pg_class中找不到也是有可能的。
解决
通过pg_relation_filenode()将oid转化为relfilenode,其结果永远是正确的,比从pg_class中查询更为准确。
因此,针对这位同学的需求,既然已经从磁盘文件中找到对应占用空间大的oid,我们就可以通过以下语句找到对应的表。
select oid,pg_relation_filenode(oid),relname from pg_class where pg_relation_filenode(oid)=...
正常情况下,通过以上命令就能找到对应的表了。
不过,如果之前系统发生了异常情况,比如在大量写入数据时突然系统宕机,那么有可能导致数据文件残留的情况。针对于这种情况,我们可以通过查看对应产生文件的时间是否是异常发生的时间,一般情况下能对应上。针对这种情况,这样的文件可以直接删除即可,当然,为了保险起见,我们可以备份到一个别的目录。
相关文章:

Greenplum 查找数据目录占用最大的表
背景 社区中某同学提出问题: 某环境磁盘占用空间较大,于是想找到数据目录占用最大的表。使用常规查询找不出来,于是到数据目录下分析filenode,找到3个filenode占了400G。然而根据filenode从pg_class中确找不到对应的relfilenode。…...
Java 基于 SpringBoot 的酒店管理系统,附源码和数据库
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W,Csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 文章目录 一、前言介绍二、系统结构三、系统详细实现3.1用户信息管理3.2会员信息管理3.3客房信息管理3.4收藏…...
LinkedList(4):多线程LinkedList 不安全情况
多线程不安全演示,线程越多,现象越明显,这边只启了四个线程。 package com.example.demo;import java.util.LinkedList; import java.util.UUID;public class LInkedListThread {public static void main(String[] args) {final LinkedList&…...
3D印刷电路板在线渲染查看工具
从概念上讲,这是有道理的,因为PCB印制电路板上的走线从一个连接到下一个连接的路线基本上是平面的。 然而,我们生活在一个 3 维世界中,能够以这种方式可视化电路以及相应的组件,对于设计过程很有帮助。本文将介绍KiCad…...

【mysql】出现 slow sql 问题及建议
文章目录 1. SQL 执行什么情况下会变慢?2. 影响 SQL 语句执行效率的主要因素有哪些?3. 慢 SQL 是如何拖垮数据库的?4. 最佳实践建议 1. SQL 执行什么情况下会变慢? ● 数据量增加:数据库中的数据量可能会逐渐增加&…...
element树形筛选
<el-inputv-model"projectName"placeholder"请输入名称"clearablemaxlength"10"clear"clearTree" /> <el-divider /> <el-treeref"tree"class"filter-tree":data"treeList":props"…...

打字侠:一款专业的中文打字网站
打字侠第一个正式版发布啦!!! 虽然离期望的样子还有一段路要走,不过能看到它正式发布,我还是很激动哟! 打字侠是一款面向中学生和大学生的在线打字软件,它通过合理的课程设计和精美的图形界面帮…...

C++ std::default_random_engine的使用
使用std::default_random_engine可生成不同分布的随机数,下面使用实例来说明其使用。 随机生成0-1间的实数 //利用当前时间生成的种子,可保证每次生成的值都不一样 unsigned seed std::chrono::system_clock::now().time_since_epoch().count(); std:…...

软件设计模式(二):工厂、门面、调停者和装饰器模式
前言 在这篇文章中,荔枝将会梳理软件设计模式中的四种:工厂模式、Facade模式、Mediator模式和装饰器Decorator模式。其中比较重要的就是工厂模式和装饰器模式,工厂模式在开发中使用的频数比较高。希望荔枝的这篇文章能讲清楚哈哈哈哈…...

pdf文件签名的问题解决
今天解决冲突的jar,结果出现下面的问题 java.lang.IllegalAccessError: tried to access method org.bouncycastle.asn1.DERNull.<init>()V from class com.itextpdf.text.pdf.security.PdfPKCS7at com.itextpdf.text.pdf.security.PdfPKCS7.getEncodedPKCS7…...
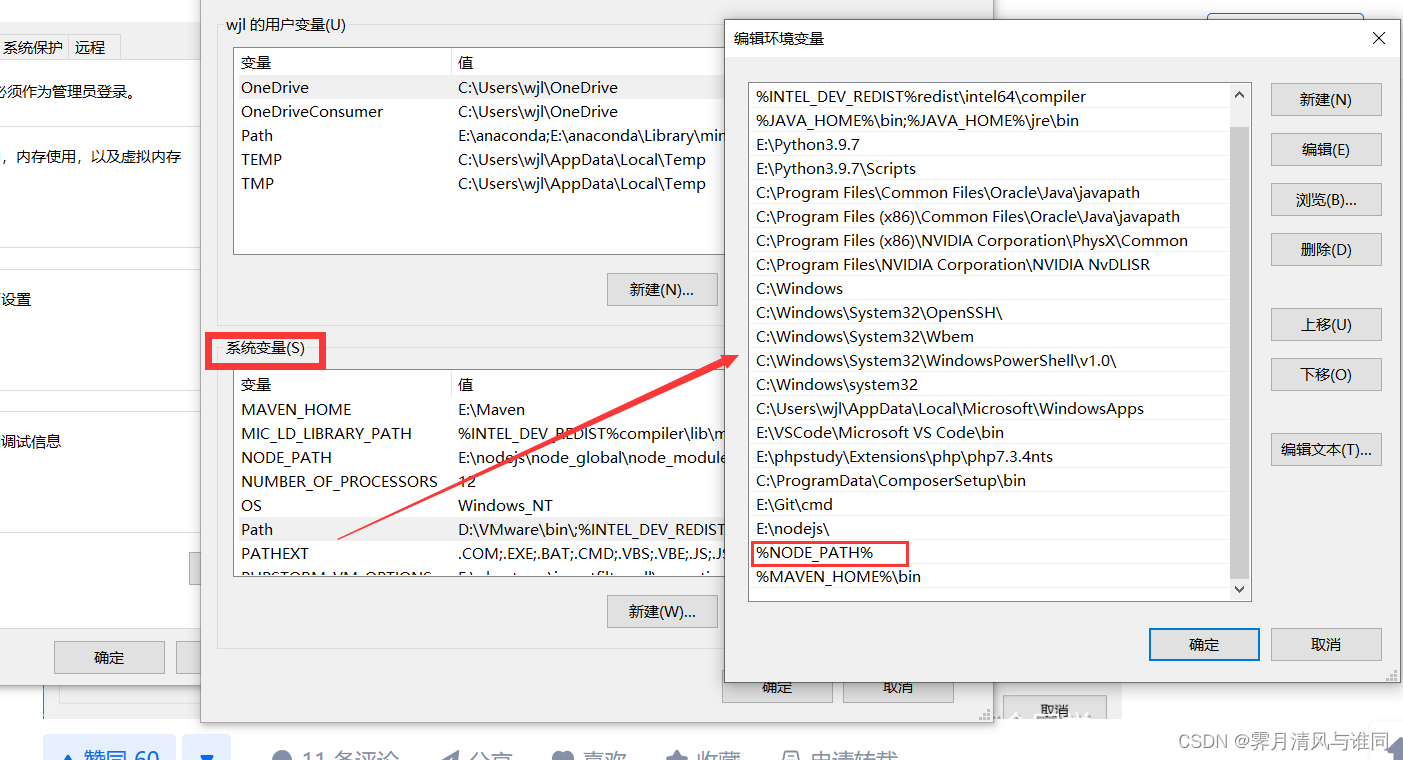
Node.js安装使用
目录 一、安装 Node.js二、环境变量配置三、npm常用命令 Node.js 是一个强大的运行时环境,它使您能够在服务器端运行 JavaScript 代码。它非常流行,用于构建 Web 应用程序、API 和各种后端服务。 一、安装 Node.js 1、访问 Node.js 官方网站。 在主页上…...

sql:SQL优化知识点记录(七)
(1)索引优化5 (2)索引优化6 (3)索引优化7 查询*, 百分号加右边,否则索引会失效 没建立索引之前都是全表扫描 没建立索引 建立索引: 建立索引 id是主键,他也…...
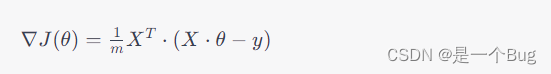
机器学习:基于梯度下降算法的线性拟合实现和原理解析
机器学习:基于梯度下降算法的线性拟合实现和原理解析 线性拟合梯度下降算法步骤算法实现数据可视化(动态展示)应用示例 当我们需要寻找数据中的趋势、模式或关系时,线性拟合和梯度下降是两个强大的工具。这两个概念在统计学、机器…...

关键点数据增强
1.关键点数据增强 # 关键点数据增强 from PIL import Image, ImageDraw import random import json from pathlib import Path# 创建一个黑色背景图像 width, height 5000, 5000 # 图像宽度和高度 background_color (0, 0, 0) # 黑色填充# 随机分布图像 num_images 1 # …...

最小化安装移动云大云操作系统--BCLinux-for-Euler-22.10-everything-x86_64-230316版
CentOS 结束技术支持,转为RHEL的前置stream版本后,国内开源Linux服务器OS生态转向了开源龙蜥和开源欧拉两大开源社区,对应衍生出了一系列商用Linux服务器系统。BCLinux-for-Euler-22.10是中国移动基于开源欧拉操作系统22.03社区版本深度定制的…...

003传统图机器学习、图特征工程
文章目录 一. 人工特征工程、连接特征二. 在节点层面对连接特征进行特征提取三. 在连接层面对连接特征进行特征提取四. 在全图层面对连接特征进行特征提取 一. 人工特征工程、连接特征 节点、连接、子图、全图都有各自的属性特征, 属性特征一般是多模态的。除属性特…...
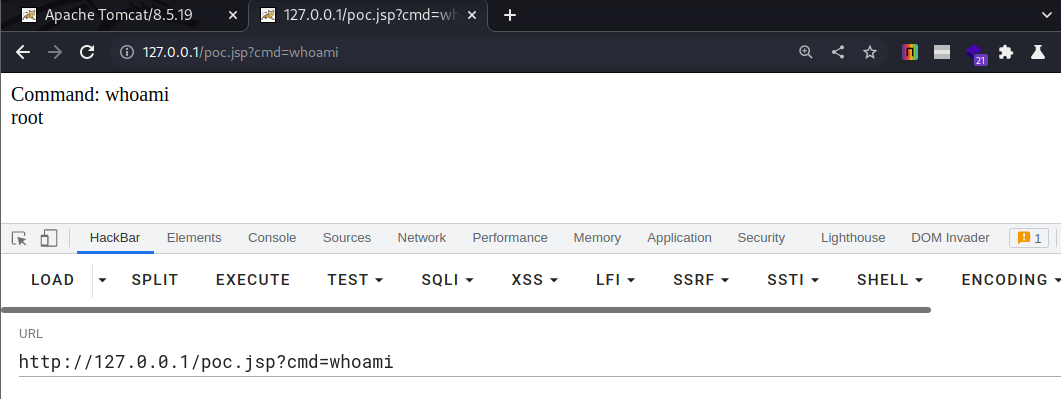
Apache Tomcat 漏洞复现
文章目录 Apache Tomcat 漏洞复现1. Tomcat7 弱密码和后端 Getshell 漏洞1.1 漏洞描述1.2 漏洞复现1.3 漏洞利用1.3.1 jsp小马1.3.2 jsp大马 1.4 安全加固 2. Aapache Tomcat AJP任意文件读取/包含漏洞2.1 漏洞描述2.1 漏洞复现2.2 漏洞利用工具2.4 修复建议 3. 通过 PUT 方法的…...

Oracle-常用权限-完整版
-- 创建用户 create user TCK identified by oracle; -- 赋权 grant connect,resource to TCK; -- 删除权限 revoke select any table from TCK -- 删除用户 CASCADE(用户下的数据级联删除) drop user TCK CASCADE -- 查询权限列表 select * from user_role_privs; select * fr…...
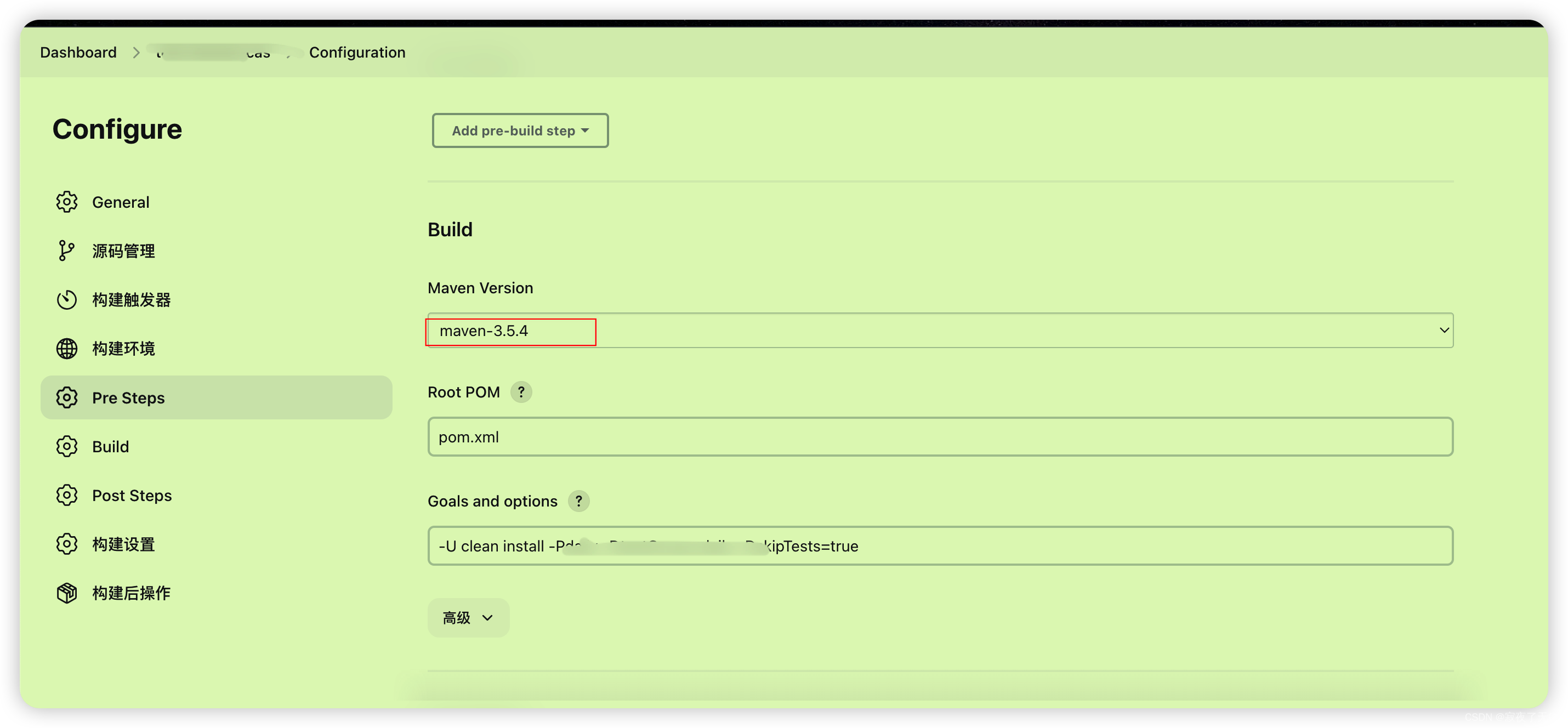
jenkins 发布job切换不同的jdk版本/ maven版本
1. 技术要求 因为有个新的项目需要使用jdk17 而旧的项目需要jdk1.8 这就需要jenkins在发布项目的时候可以指定jdk版本 2. 解决 jenkins全局工具配置页面 配置新的jdk 路径 系统管理-> 全局工具配置 如上新增个jdk 名称叫 jdk-17 然后配置jdk-17的根路径即可(这…...
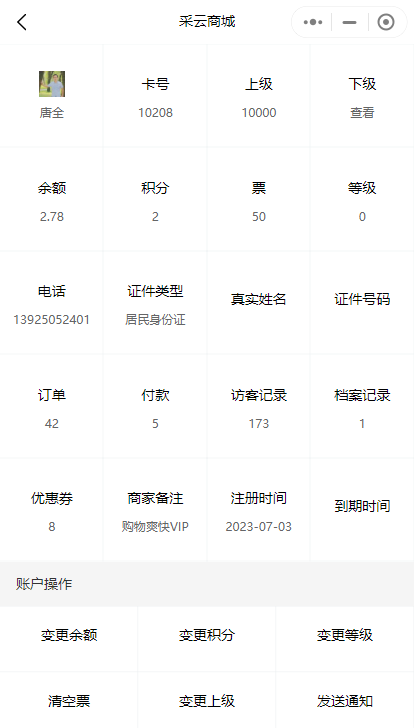
如何在小程序中给会员设置备注
给会员设置备注是一项非常有用的功能,它可以帮助商家更好地管理和了解自己的会员。下面是一个简单的教程,告诉商家如何在小程序中给会员设置备注。 1. 找到指定的会员卡。在管理员后台->会员管理处,找到需要设置备注的会员卡。也支持对会…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
