机器学习:基于梯度下降算法的线性拟合实现和原理解析
机器学习:基于梯度下降算法的线性拟合实现和原理解析
- 线性拟合
- 梯度下降
- 算法步骤
- 算法实现
- 数据可视化(动态展示)
- 应用示例
当我们需要寻找数据中的趋势、模式或关系时,线性拟合和梯度下降是两个强大的工具。这两个概念在统计学、机器学习和数据科学领域都起着关键作用。本篇博客将介绍线性拟合和梯度下降的基本原理,以及它们在实际问题中的应用。
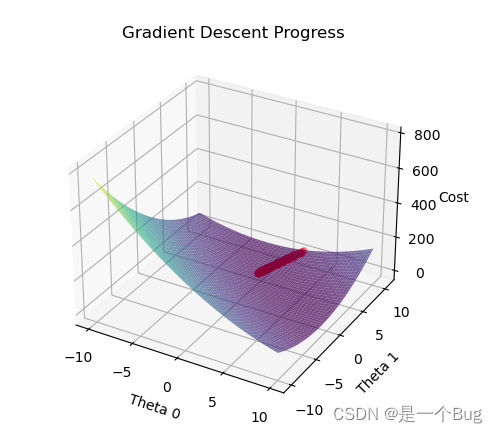
线性拟合
线性拟合是一种用于找到数据集中线性关系的方法。它的基本原理是,我们可以使用线性方程来描述两个或多个变量之间的关系。这个方程通常采用以下形式:
y = m x + b y=mx+b y=mx+b
在这个方程中, y y y 是因变量, x x x 是自变量, m m m 是斜率, b b b 是截距。线性拟合的目标是找到最佳的斜率和截距,以使线性方程最好地拟合数据。
为了找到最佳拟合线,我们通常使用最小二乘法。这意味着我们将所有数据点到拟合线的距离的平方相加,然后寻找最小化这个总和的斜率和截距。这可以用数学优化方法来实现,其中一个常用的方法就是梯度下降。
梯度下降
梯度下降是一种迭代优化算法,用于寻找函数的最小值。在线性拟合中,我们的目标是最小化误差函数,即数据点到拟合线的距离的平方和。这个误差函数通常表示为 J ( m , b ) J(m, b) J(m,b),其中 m m m 是斜率, b b b 是截距。我们的任务是找到 m m m 和 b b b 的值,使 J ( m , b ) J(m, b) J(m,b) 最小化。
梯度下降的基本思想是从一个随机初始点开始,然后根据误差函数的梯度方向逐步调整参数,直到找到局部最小值。梯度下降的迭代规则如下:
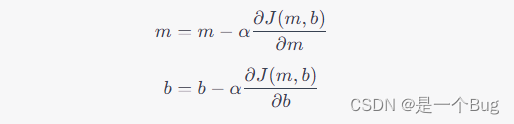
在这里, α \alpha α 是学习率,它决定了每次迭代中参数更新的步长。较大的学习率可能导致快速收敛,但可能会错过最小值,而较小的学习率可能需要更多的迭代。
算法步骤
线性回归中的梯度下降是一种优化算法,用于寻找最佳拟合线性模型的参数,以最小化预测值与实际观测值之间的均方误差(Mean Squared Error,MSE)。梯度下降的原理可以概括为以下几个步骤:
初始化参数: 首先,为线性回归模型的参数(权重和偏置项)选择初始值。通常,可以随机初始化这些参数。
计算损失函数: 使用当前的参数值,计算出模型的预测值,并计算预测值与实际观测值之间的差异,即损失函数。在线性回归中,常用的损失函数是均方误差(MSE),它表示为:
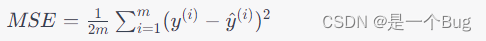
其中, m m m 是样本数量, y ( i ) y^{(i)} y(i) 是第 i i i 个观测值, y ^ ( i ) \hat{y}^{(i)} y^(i) 是模型的预测值。
计算梯度: 梯度是损失函数关于参数的偏导数,表示了损失函数在参数空间中的变化方向。梯度下降算法通过计算损失函数关于参数的梯度来确定参数更新的方向。对于线性回归模型,梯度可以表示为:
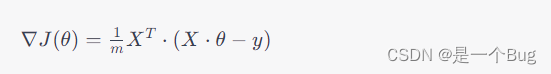
其中, J ( θ ) J(\theta) J(θ) 是损失函数, θ \theta θ 是参数向量, X X X 是特征矩阵, y y y 是目标向量。
参数更新: 使用梯度信息,按照下面的规则来更新参数:
θ = θ − α ∇ J ( θ ) θ=θ−α∇J(θ) θ=θ−α∇J(θ)
其中, α \alpha α 是学习率,它控制着每次参数更新的步长。学习率越小,参数更新越小,但收敛可能会更稳定。学习率越大,参数更新越快,但可能会导致不稳定的收敛或发散。
重复迭代: 重复执行步骤2至步骤4,直到满足停止条件,例如达到最大迭代次数或损失函数收敛到一个足够小的值。在每次迭代中,参数都会根据梯度信息进行更新,逐渐优化以减小损失函数。
梯度下降的目标是找到损失函数的最小值,这将使线性回归模型的预测值与实际观测值之间的误差最小化。通过不断调整参数,梯度下降可以使模型逐渐收敛到最佳参数值,从而得到最佳拟合线性模型。
算法实现
import numpy as np
import matplotlib.pyplot as plt
# 设置字体为支持汉字的字体(例如宋体)
plt.rcParams['font.sans-serif'] = ['SimSun']
# 创建示例数据
X = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 5])# 添加偏置项(截距项)到特征矩阵
# 添加了偏置项(截距项)到特征矩阵 X。这是通过在 X 前面添加一列全为1的列来实现的。这是线性回归模型中的常见步骤。
X_b = np.c_[np.ones((len(X), 1)), X.reshape(-1, 1)]# 使用正规方程计算最佳参数
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)# 使用梯度下降计算最佳参数
def gradient_descent(X_b, y, theta, learning_rate, num_epochs):m = len(y)losses = []for epoch in range(num_epochs):# 计算当前参数下的预测值。predictions = X_b.dot(theta)error = predictions - y# 计算均方误差(MSE)作为损失函数,衡量预测值和实际值之间的差异。loss = np.mean(error**2)# 计算损失函数的梯度,用于更新参数。# X_b.T 表示矩阵 X_b 的转置。在线性代数中,矩阵的转置是指将矩阵的行和列交换,即将矩阵的列向量变成行向量,反之亦然。gradient = 2 * X_b.T.dot(error) / mtheta -= learning_rate * gradientlosses.append(loss)return theta, lossestheta = np.random.randn(2)
learning_rate = 0.01
num_epochs = 1000
theta, losses = gradient_descent(X_b, y, theta, learning_rate, num_epochs)# 可视化数据和拟合结果
plt.scatter(X, y, label='数据点')
plt.plot(X, X_b.dot(theta_best), label='正规方程拟合', color='green')
plt.plot(X, X_b.dot(theta), label='梯度下降拟合', color='red')
plt.xlabel('特征值')
plt.ylabel('目标值')
plt.legend()
plt.show()数据可视化(动态展示)
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation# 创建一些示例数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.rand(100, 1)# 初始化线性模型参数
theta = np.random.randn(2, 1)def gradient_descent(X, y, theta, learning_rate, num_iterations):m = len(y)history = []for iteration in range(num_iterations):gradients = -2/m * X.T.dot(y - X.dot(theta))theta -= learning_rate * gradientshistory.append(theta.copy())return historylearning_rate = 0.1
num_iterations = 50# 添加偏置项
X_b = np.c_[np.ones((100, 1)), X]# 执行梯度下降算法并获取参数历史
parameter_history = gradient_descent(X_b, y, theta, learning_rate, num_iterations)# 创建动态可视化
fig, ax = plt.subplots()
line, = ax.plot([], [], lw=2)def animate(i):y_pred = X_b.dot(parameter_history[i])line.set_data(X, y_pred)return line,ani = FuncAnimation(fig, animate, frames=num_iterations, interval=200)
plt.scatter(X, y)
plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression with Gradient Descent')plt.show()
应用示例
线性拟合和梯度下降在各种领域都有广泛的应用。以下是一些示例:
股市预测:通过线性拟合历史股票价格数据,可以尝试预测未来股价的趋势。
房价预测:使用线性拟合来估算房屋价格与特征(如面积、位置等)之间的关系,帮助买家和卖家做出决策。
机器学习模型训练:梯度下降是训练线性回归、逻辑回归和神经网络等机器学习模型的关键步骤。
自然语言处理:在自然语言处理中,线性拟合可以用于情感分析和文本分类任务。
总之,线性拟合和梯度下降是数据科学和机器学习领域的基本工具,它们帮助我们理解数据中的关系,并训练模型以做出预测和决策。这两个概念的理解对于处理各种数据分析和机器学习问题都至关重要。希望本博客能够帮助你更好地理解它们的基本原理和应用。
相关文章:
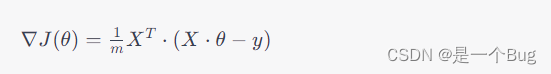
机器学习:基于梯度下降算法的线性拟合实现和原理解析
机器学习:基于梯度下降算法的线性拟合实现和原理解析 线性拟合梯度下降算法步骤算法实现数据可视化(动态展示)应用示例 当我们需要寻找数据中的趋势、模式或关系时,线性拟合和梯度下降是两个强大的工具。这两个概念在统计学、机器…...

关键点数据增强
1.关键点数据增强 # 关键点数据增强 from PIL import Image, ImageDraw import random import json from pathlib import Path# 创建一个黑色背景图像 width, height 5000, 5000 # 图像宽度和高度 background_color (0, 0, 0) # 黑色填充# 随机分布图像 num_images 1 # …...

最小化安装移动云大云操作系统--BCLinux-for-Euler-22.10-everything-x86_64-230316版
CentOS 结束技术支持,转为RHEL的前置stream版本后,国内开源Linux服务器OS生态转向了开源龙蜥和开源欧拉两大开源社区,对应衍生出了一系列商用Linux服务器系统。BCLinux-for-Euler-22.10是中国移动基于开源欧拉操作系统22.03社区版本深度定制的…...

003传统图机器学习、图特征工程
文章目录 一. 人工特征工程、连接特征二. 在节点层面对连接特征进行特征提取三. 在连接层面对连接特征进行特征提取四. 在全图层面对连接特征进行特征提取 一. 人工特征工程、连接特征 节点、连接、子图、全图都有各自的属性特征, 属性特征一般是多模态的。除属性特…...
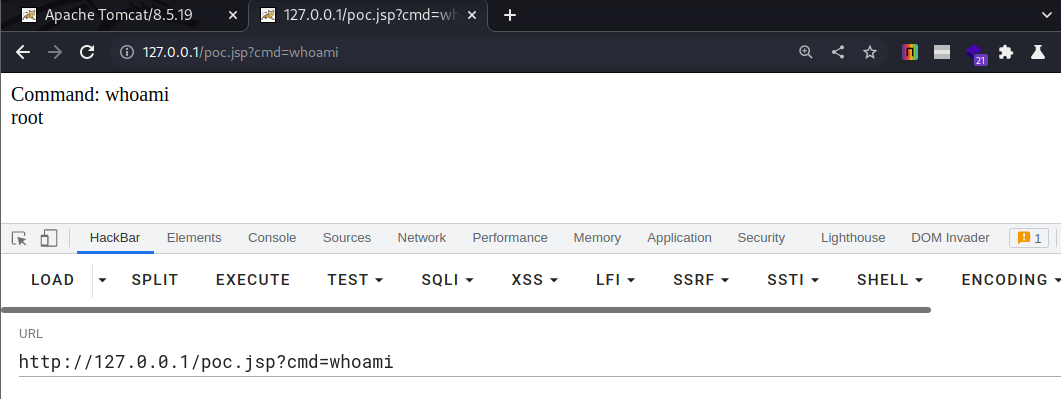
Apache Tomcat 漏洞复现
文章目录 Apache Tomcat 漏洞复现1. Tomcat7 弱密码和后端 Getshell 漏洞1.1 漏洞描述1.2 漏洞复现1.3 漏洞利用1.3.1 jsp小马1.3.2 jsp大马 1.4 安全加固 2. Aapache Tomcat AJP任意文件读取/包含漏洞2.1 漏洞描述2.1 漏洞复现2.2 漏洞利用工具2.4 修复建议 3. 通过 PUT 方法的…...

Oracle-常用权限-完整版
-- 创建用户 create user TCK identified by oracle; -- 赋权 grant connect,resource to TCK; -- 删除权限 revoke select any table from TCK -- 删除用户 CASCADE(用户下的数据级联删除) drop user TCK CASCADE -- 查询权限列表 select * from user_role_privs; select * fr…...
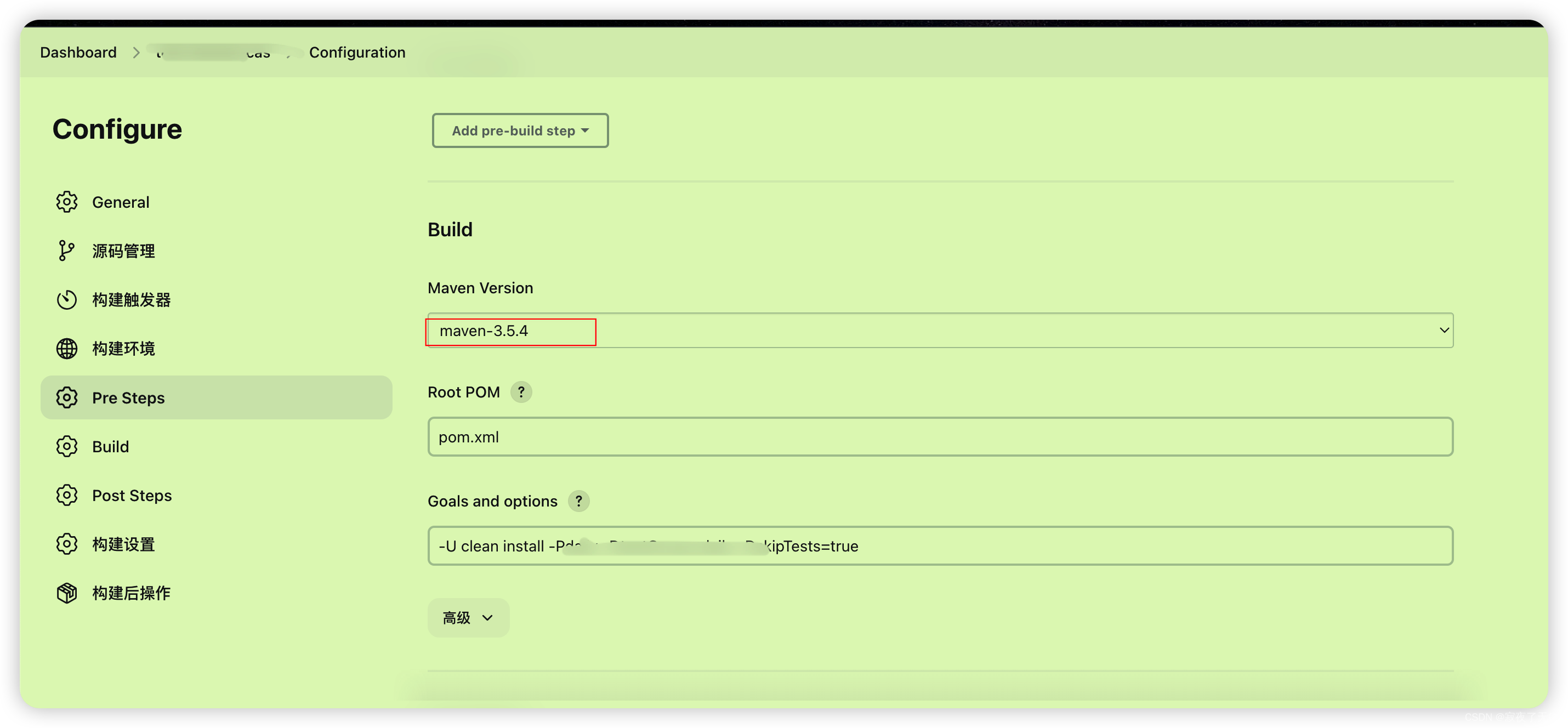
jenkins 发布job切换不同的jdk版本/ maven版本
1. 技术要求 因为有个新的项目需要使用jdk17 而旧的项目需要jdk1.8 这就需要jenkins在发布项目的时候可以指定jdk版本 2. 解决 jenkins全局工具配置页面 配置新的jdk 路径 系统管理-> 全局工具配置 如上新增个jdk 名称叫 jdk-17 然后配置jdk-17的根路径即可(这…...
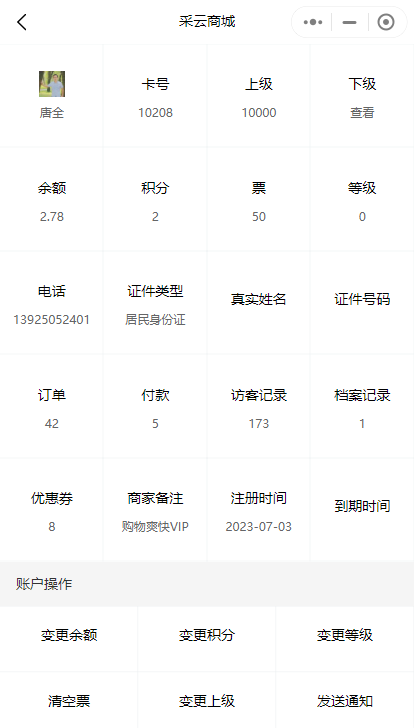
如何在小程序中给会员设置备注
给会员设置备注是一项非常有用的功能,它可以帮助商家更好地管理和了解自己的会员。下面是一个简单的教程,告诉商家如何在小程序中给会员设置备注。 1. 找到指定的会员卡。在管理员后台->会员管理处,找到需要设置备注的会员卡。也支持对会…...
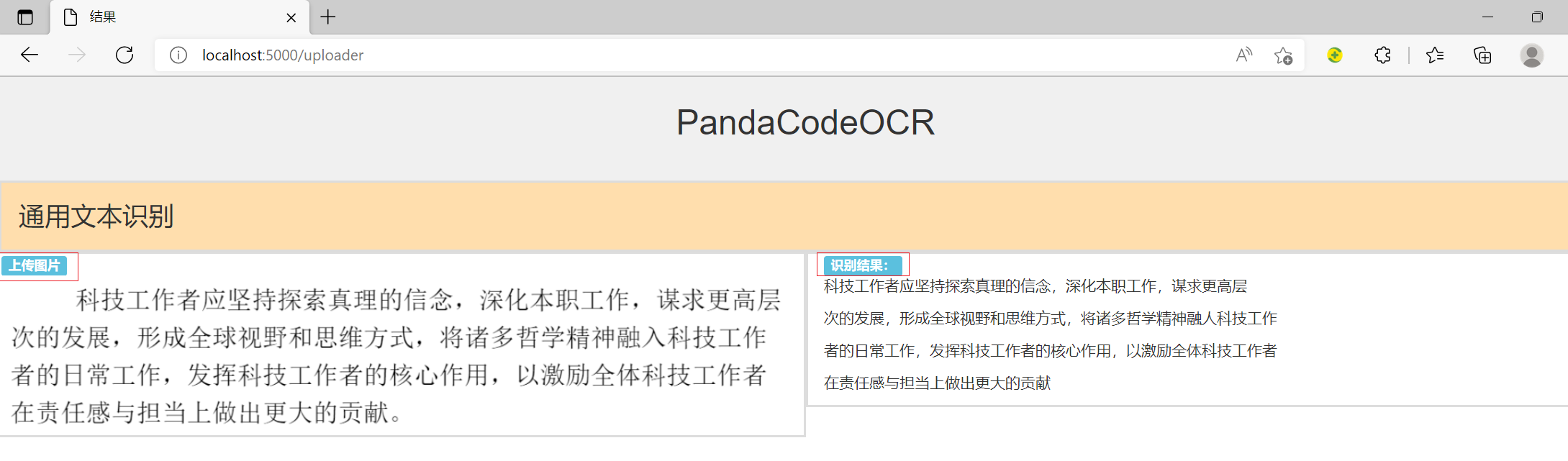
PaddleOCR学习笔记2-初步识别服务
今天初步实现了网页,上传图片,识别显示结果到页面的服务。后续再完善。 采用flask paddleocr bootstrap快速搭建OCR识别服务。 代码结构如下: 模板页面代码文件如下: upload.html : <!DOCTYPE html> <html> <…...

【Opencv】Pyhton 播放上一帧,下一帧,存video,逐帧分析
文章目录 读取具体哪一帧等待按钮写入解码方式与文件格式对应全部代码 读取具体哪一帧 这个方法可以获取某一帧: while True:cap.set(cv2.CAP_PROP_POS_FRAMES, current_frame)ret, frame cap.read()if not ret:break等待按钮 这个方法可以显示当前帧,…...
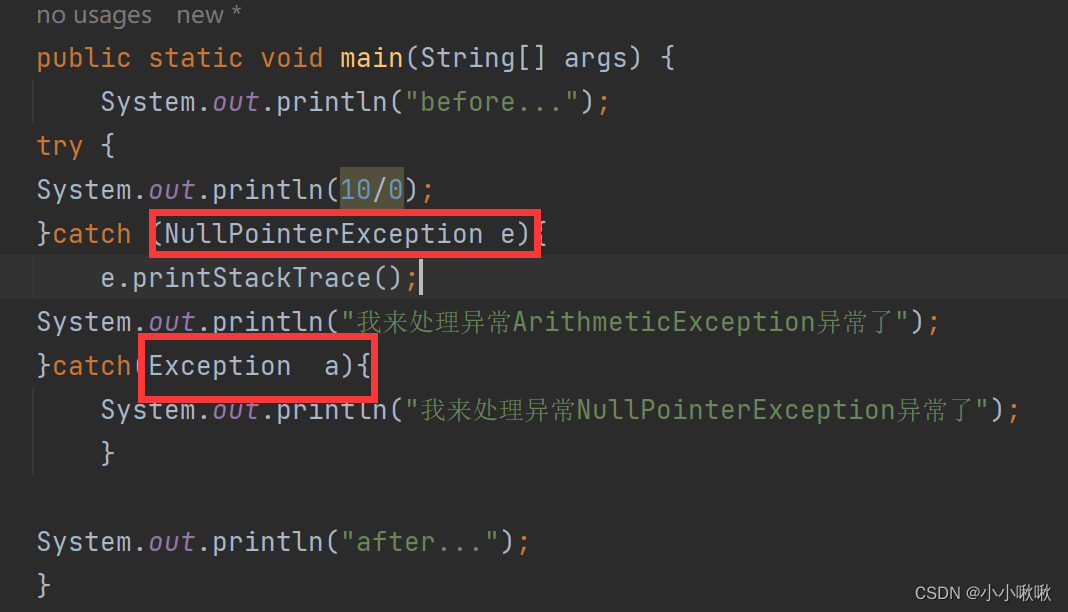
【关于Java:认识异常】
文章目录 一、1. 异常概念与体系结构1.1 异常的概念1.2 常见的异常1.算数异常2.数组越界异常3.空指针异常 1.3 异常的体系结构1.4 异常的分类1. 编译时异常2. 运行时异常(RuntimeException) 二、 异常的处理方式2.1 防御式编程2.2 EAFP:(异常…...

【C++ • STL • 力扣】详解string相关OJ
文章目录 1、仅仅翻转字母2、字符串中的第一个唯一字符3、字符串里最后一个单词的长度4、验证一个字符串是否是回文5、字符串相加总结 ヾ(๑╹◡╹)ノ" 人总要为过去的懒惰而付出代价 ヾ(๑╹◡╹)ノ" 1、仅仅翻转字母 力扣链接 代码1展示&…...
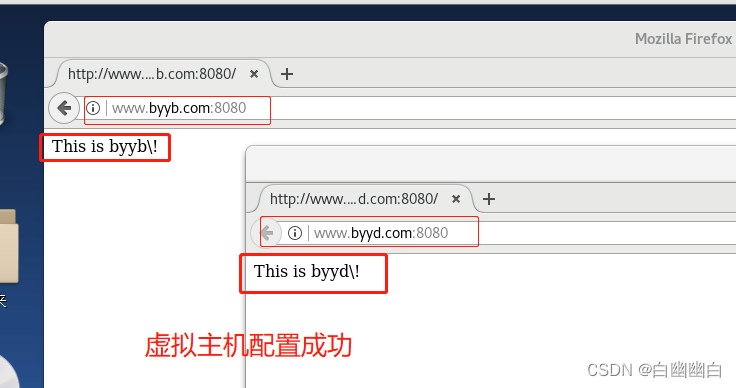
【Tomcat服务部署及优化】
Tomcat 一、什么是Tomcat?二、Tomcat 核心组件2.1 Tomcat 组件2.3 Container组件的结构2.4 Tomcat 请求过程 三、Tomcat 部署3.1 安装JDK3.2 设置JDK环境变量3.3 安装Tomcat并用supervisor启动解压添加到supervisord服务测试能否通过supervisorctl启动 四、Tomcat的端口和主要…...
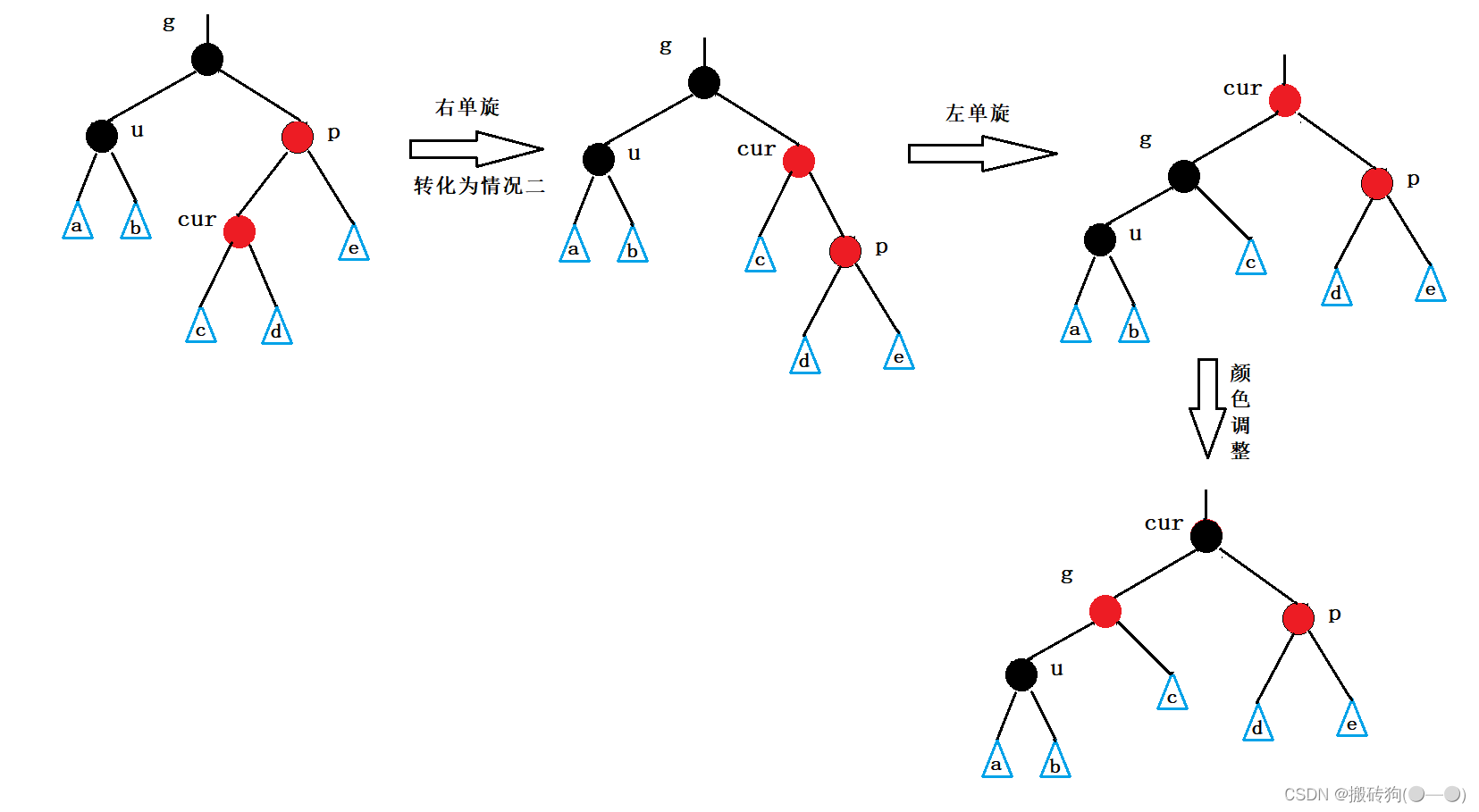
C++之红黑树
红黑树 红黑树的概念红黑树的性质红黑树结点的定义红黑树的插入红黑树的验证红黑树与AVL树的比较 红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上…...
TCP)
Go语言网络编程(socket编程)TCP
1、TCP编程 1.1.1 Go语言实现TCP通信 TCP协议 TCP/IP(Transmission Control Protocol/Internet Protocol) 即传输控制协议/网间协议,是一种面向连接(连接导向)的、可靠的、基于字节流的传输层(Transport layer)通信协…...

C语言——局部和全局变量
局部变量 定义在函数内部的变量称为局部变量(Local Variable) 局部变量的作用域(作用范围)仅限于函数内部, 离开该函数后是无效的 离开该函数后,局部变量自动释放 示例代码: #include <stdio.h>// 函数定义 …...
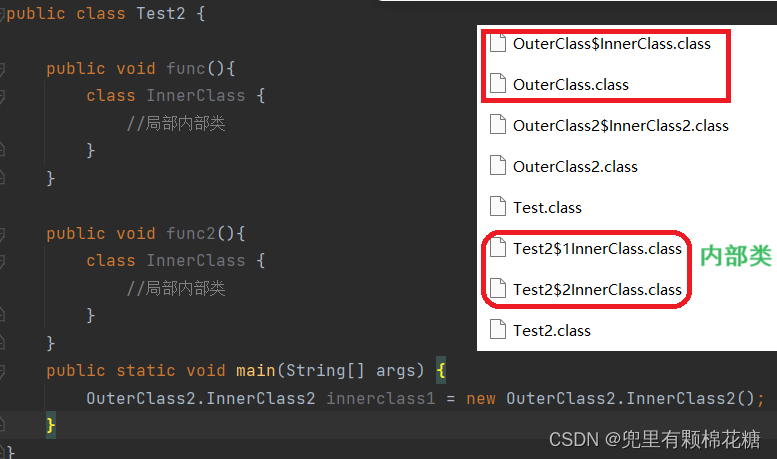
【Java基础篇 | 类和对象】--- 聊聊什么是内部类
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【JavaSE_primary】 本专栏旨在分享学习Java的一点学习心得,欢迎大家在评论区讨论💌 前言 当一个事物的内部&…...

合宙Air724UG LuatOS-Air LVGL API控件-页面 (Page)
页面 (Page) 当控件内容过多,无法在屏幕内完整显示时,可让其在 页面 内显示。 示例代码 page lvgl.page_create(lvgl.scr_act(), nil) lvgl.obj_set_size(page, 150, 200) lvgl.obj_align(page, nil, lvgl.ALIGN_CENTER, 0, 0)label lvgl.label_crea…...
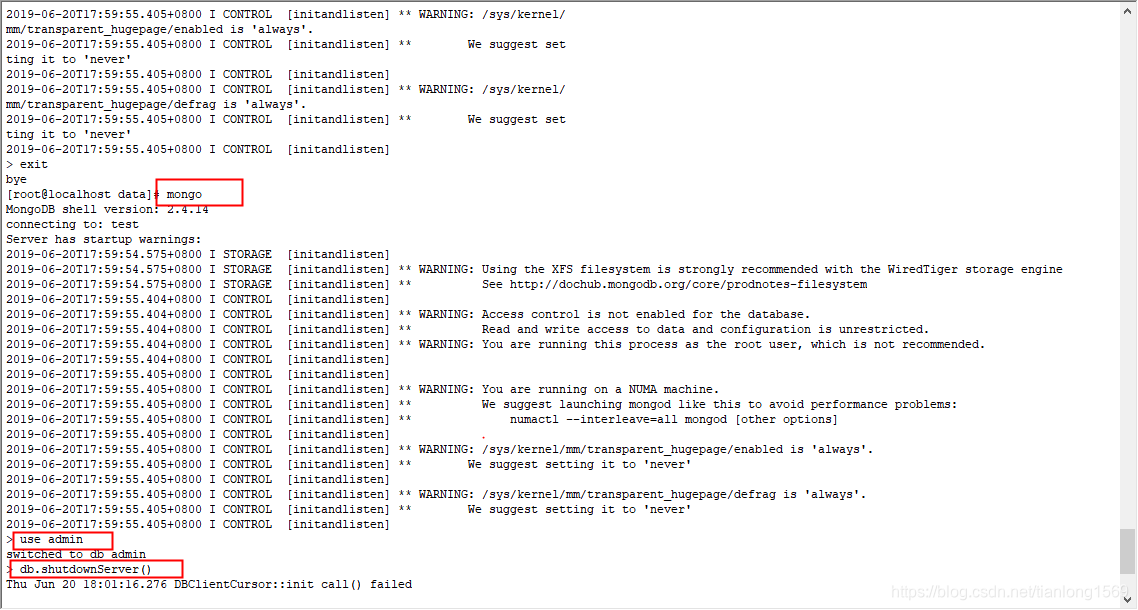
mongodb数据库操作
1、启动mongodb /usr/local/mongodb/bin/mongod --dbpath /var/mongodb/data/--logpath /var/mongodb/logs/log.log &在mongodb启动命令中 --dbpath 指定mongodb的数据存储路径 --logpath 指定mongodb的日志存储路径 2、停止mongodb 第一步先进入mongo命令行模式 第二…...
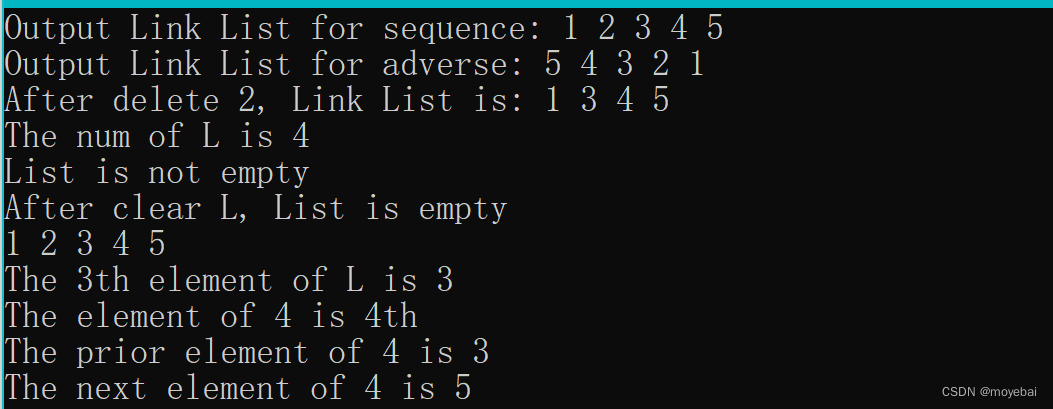
第 2 章 线性表 ( 双链循环线性表(链式存储结构)实现)
1. 背景说明 2. 示例代码 1) status.h /* DataStructure 预定义常量和类型头文件 */#ifndef STATUS_H #define STATUS_H#define CHECK_NULL(pointer) if (!(pointer)) { \printf("FuncName: %-15s Line: %-5d ErrorCode: %-3d\n", __func__, __LINE__, ERR_NULL_PTR…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
