B - Polycarp‘s Practice
Polycarp is practicing his problem solving skill. He has a list of nn problems with difficulties a_1, a_2, \dots, a_na1,a2,…,an, respectively. His plan is to practice for exactly kk days. Each day he has to solve at least one problem from his list. Polycarp solves the problems in the order they are given in his list, he cannot skip any problem from his list. He has to solve all nn problems in exactly kk days.
Thus, each day Polycarp solves a contiguous sequence of (consecutive) problems from the start of the list. He can't skip problems or solve them multiple times. As a result, in kk days he will solve all the nn problems.
The profit of the jj-th day of Polycarp's practice is the maximum among all the difficulties of problems Polycarp solves during the jj-th day (i.e. if he solves problems with indices from ll to rr during a day, then the profit of the day is \max\limits_{l \le i \le r}a_il≤i≤rmaxai). The total profit of his practice is the sum of the profits over all kk days of his practice.
You want to help Polycarp to get the maximum possible total profit over all valid ways to solve problems. Your task is to distribute all nn problems between kk days satisfying the conditions above in such a way, that the total profit is maximum.
For example, if n = 8, k = 3n=8,k=3 and a = [5, 4, 2, 6, 5, 1, 9, 2]a=[5,4,2,6,5,1,9,2], one of the possible distributions with maximum total profit is: [5, 4, 2], [6, 5], [1, 9, 2][5,4,2],[6,5],[1,9,2]. Here the total profit equals 5 + 6 + 9 = 205+6+9=20.
Input
The first line of the input contains two integers nn and kk (1 \le k \le n \le 20001≤k≤n≤2000) — the number of problems and the number of days, respectively.
The second line of the input contains nn integers a_1, a_2, \dots, a_na1,a2,…,an (1 \le a_i \le 20001≤ai≤2000) — difficulties of problems in Polycarp's list, in the order they are placed in the list (i.e. in the order Polycarp will solve them).
Output
In the first line of the output print the maximum possible total profit.
In the second line print exactly kk positive integers t_1, t_2, \dots, t_kt1,t2,…,tk (t_1 + t_2 + \dots + t_kt1+t2+⋯+tk must equal nn), where t_jtj means the number of problems Polycarp will solve during the jj-th day in order to achieve the maximum possible total profit of his practice.
If there are many possible answers, you may print any of them.
Sample 1
| Inputcopy | Outputcopy |
|---|---|
8 3 5 4 2 6 5 1 9 2 | 20 3 2 3 |
Sample 2
| Inputcopy | Outputcopy |
|---|---|
5 1 1 1 1 1 1 | 1 5 |
Sample 3
| Inputcopy | Outputcopy |
|---|---|
4 2 1 2000 2000 2 | 4000 2 2 |
Note
The first example is described in the problem statement.
In the second example there is only one possible distribution.
In the third example the best answer is to distribute problems in the following way: [1, 2000], [2000, 2][1,2000],[2000,2]. The total profit of this distribution is 2000 + 2000 = 40002000+2000=4000.
题目翻译
给定长度为n的序列,要求分成k段,最大化每段最大值的和
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<cmath>
#include<string.h>
#include<climits>
#include<map>
#include<algorithm>
typedef long long ll;
using namespace std;
const int N = 2010;
int n, k;struct node {int num, val;
}mm[N];bool cmp1(node n1, node n2)
{return n1.val > n2.val;
}bool cmp2(node n1, node n2)
{return n1.num < n2.num;
}int main()
{cin >> n >> k;for (int i = 1; i <= n; i++){int num;cin >> num;mm[i].num = i;mm[i].val = num;}sort(mm + 1, mm + n + 1, cmp1);//先对整个序列按照数值的大小进行排序,去前k个数的和int sum = 0;for (int i = 1; i <= k; i++) sum += mm[i].val;sort(mm + 1, mm + k + 1, cmp2); //在对前k个数进行排序,做差分组cout << sum << endl;for (int i = 1; i < k; i++) cout << mm[i].num - mm[i - 1]. num << " ";cout << n - mm[k - 1].num << endl;return 0;
}相关文章:

B - Polycarp‘s Practice
Polycarp is practicing his problem solving skill. He has a list of nn problems with difficulties a_1, a_2, \dots, a_na1,a2,…,an, respectively. His plan is to practice for exactly kk days. Each day he has to solve at least one problem from his list. …...

朴素贝叶斯数据分类------
------------------后期会编辑些关于朴素贝叶斯算法的推导及代码分析----------------- import numpy as np import pandas as pd from sklearn.model_selection import train_test_split from sklearn.naive_bayes import GaussianNB, BernoulliNB, MultinomialNB from sklear…...
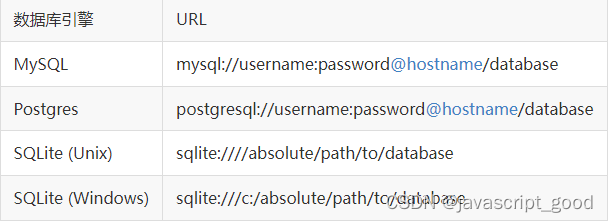
flask中的操作数据库的插件Flask-SQLAlchemy
1、ORM 框架 Web 开发中,一个重要的组成部分便是数据库了。Web 程序中最常用的莫过于关系型数据库了,也称 SQL 数据库。另外,文档数据库(如 mongodb)、键值对数据库(如 redis)近几年也逐渐在 w…...

arrow的使用
pandas2.0引入了pyarrow作为可选后端,比numpy的性能提高很多,所以为了改造backtrader,用cython和c++重写整个框架,准备用arrow作为底层的数据结构(backtrader现在的底层数据结构是基于python array构建的) 安装arrow推荐使用vcpkg git clone https://github.com/Microsoft…...
))
【24种设计模式】装饰器模式(Decorator Pattern(Wrapper))
装饰器模式 装饰器模式是一种结构型设计模式,用于动态地给对象添加额外的行为或责任,而不需要改变原始对象的结构。通过创建一个包装器类(装饰器),它包含原始对象的引用,并提供与原始对象相同的接口&#…...

小程序v-for与key值使用
小程序中的v-for和key与Vue中的用法基本相同。v-for用于循环渲染列表,key用于给每个循环项分配一个唯一的标识。 使用v-for时,通常建议使用wx:for代替,例如: <view wx:for"{{ items }}" wx:key"id">{…...
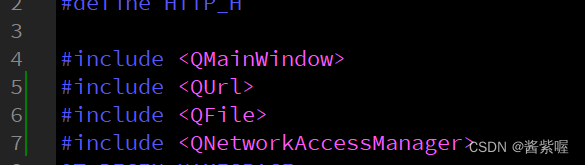
Qt包含文件不存在问题解决 QNetworkAccessManager
这里用到了Qt的网络模块,在.pro中添加了 QT network 但是添加 #include <QNetworkAccessManager> 会报错说找不到,可以通过在项目上右键执行qmake后,直接#include <QNetworkAccessManager>就不会报错了:...
【视频图像篇】FastStone Capture屏幕长截图软件
【视频图像篇】FastStone Capture屏幕长截图软件 FastStone Capture最常用的一款屏幕长截图软件—【蘇小沐】 文章目录 【视频图像篇】FastStone Capture屏幕长截图软件实验环境1、启动界面2、自定义工具栏3、自动保存 (一)长截图1、捕获滚动窗口2、捕获…...
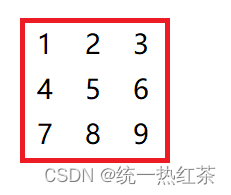
【C语言】每日一题(杨氏矩阵查找数)
目录 杨氏矩阵介绍:方法:思路:代码实现: 杨氏矩阵介绍: 既然在杨氏矩阵中查找数,那什么是杨氏矩阵呢? 矩阵的每行从左到右是递增的,矩阵从上到下是递增的。 例如: 方法…...
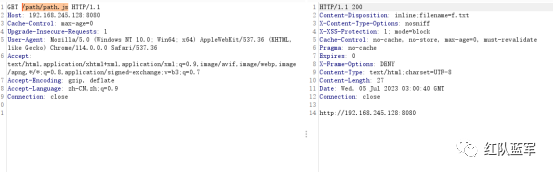
探究SpringWeb对于请求的处理过程
探究目的 在路径归一化被提出后,越来越多的未授权漏洞被爆出,而这些未授权多半跟spring自身对路由分发的处理机制有关。今天就来探究一下到底spring处理了什么导致了才导致鉴权被绕过这样严重的问题。 DispatcherServlet介绍 首先在分析spring对请求处…...
如何使用Google Compute Engine入门指南快速创建和配置您的云虚拟机实例
文章目录 步骤1:创建 Google Cloud Platform(GCP)账户步骤2:设置 GCP 项目步骤3:启用 Google Compute Engine API步骤4:安装 Google Cloud SDK步骤5:创建虚拟机实例步骤6:连接到虚拟…...

springMVC中全局异常处理
前言: 当不同方法执行时,抛出相同异常。为了简约代码和避免重复使用try{}catch{}。此时使用统一异常处理。但局部的统一异常处理只能为所在类所调用。因此产生全局异常处理,该类中统一异常处理方法可以作用于整个controller。(以…...

【Nginx24】Nginx学习:压缩模块Gzip
Nginx学习:压缩模块Gzip 又是一个非常常见的模块,Gzip 现在也是事实上的 Web 应用压缩标准了。随便打开一个网站,在请求的响应头中都会看到 Content-Encoding: gzip 这样的内容,这就表明当前这个请求的页面或资源使用了 Gzip 压缩…...
)
我的私人笔记(zookeeper分布式安装)
分布式安装 1.安装前准备 (1)下载zookeeper:Index of /dist/zookeeper(当前使用为3.4.10版本) (2)安装JDK (3)拷贝zookeeper安装包到Linux系统下 (4)解压到指定目录 tar -xzvf zookeeper-3.4.10.tar.gz -C /opt/servers/ (5)修改名称 …...

小程序排名优化全攻略
随着小程序的快速发展,小程序之间的竞争也日益激烈。如何在竞争对手众多的环境下脱颖而出,通过小程序排名优化来提高曝光率和流量转化率,已成为许多小程序开发者和运营者关注的重点。本文将全面解析小程序排名优化的方法,让您可以更好地提升小程序的搜索排名。 【名即微】 小程…...

MySQL MHA
什么是 MHA MHA(Master High Availability)是一套优秀的MySQL高可用环境下故障切换和主从复制的软件 MHA 的出现就是解决MySQL 单点故障的问题 MySQL故障切换过程中,MHA能做到0-30秒内自动完成故障切换操作 MHA能在故障切换的过程中最大程度上…...
)
Java API速记手册(持续更新ing...)
诸神缄默不语-个人CSDN博文目录 之所以干这个事原因也很简单,因为我3年没写Java了,现在在复健。 因为我最近都在用Python,所以跟Python一样的部分我就不写了。 最基本的框架public class MainClass {public static void main(String[] args…...
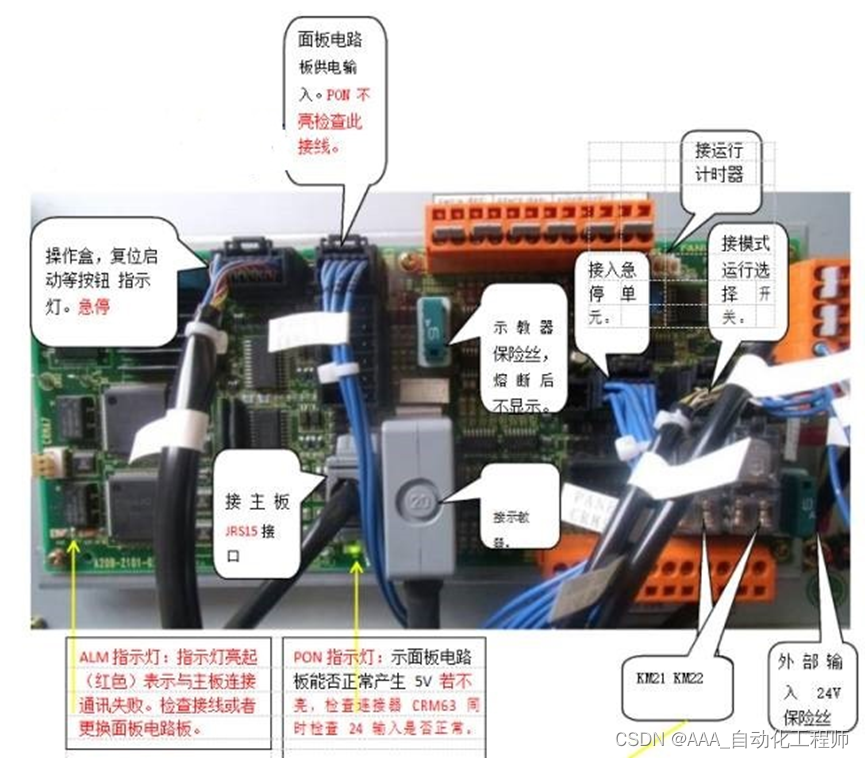
FANUC机器人电气控制柜内部硬件电路和模块详细介绍
FANUC机器人电气控制柜内部硬件电路和模块详细介绍 PSU电源单元 通过背板传输了如下电源 +5 +2.0V +3.3 +24v +24E +15V -15V 主板--接口描述: 主板内部结构: 面板电路板: 引申一下 KM21 与 KM22 的作用它们分别接至操作面板上上的急停按...

LGFormer:LOCAL TO GLOBAL TRANSFORMER FOR VIDEO BASED 3D HUMAN POSE ESTIMATION
基于视频的三维人体姿态估计的局部到全局Transformer 作者:马海峰 *,陆克 * †,薛健 *,牛泽海 *,高鹏程† * 中国科学院大学工程学院,北京100049 鹏程实验室,深圳518055 来源:202…...
数据结构零基础入门篇(C语言实现)
前言:数据结构属于C学习中较难的一部分,对应学习者的要求较高,如基础不扎实,建议着重学习C语言中的指针和结构体,万丈高楼平地起。 目录: 一,链表 1)单链表的大致结构实现 2&…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
