【C++进阶】:AVL树(平衡因子)
AVL树
- 一.概念
- 二.插入
- 1.搜索二叉树
- 2.平衡因子
- 三.旋转
- 1.更新平衡因子
- 2.旋转
- 1.左单旋
- 2.右单旋
- 3.先右旋再左旋
- 4.先左旋再右旋
- 四.完整代码
一.概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
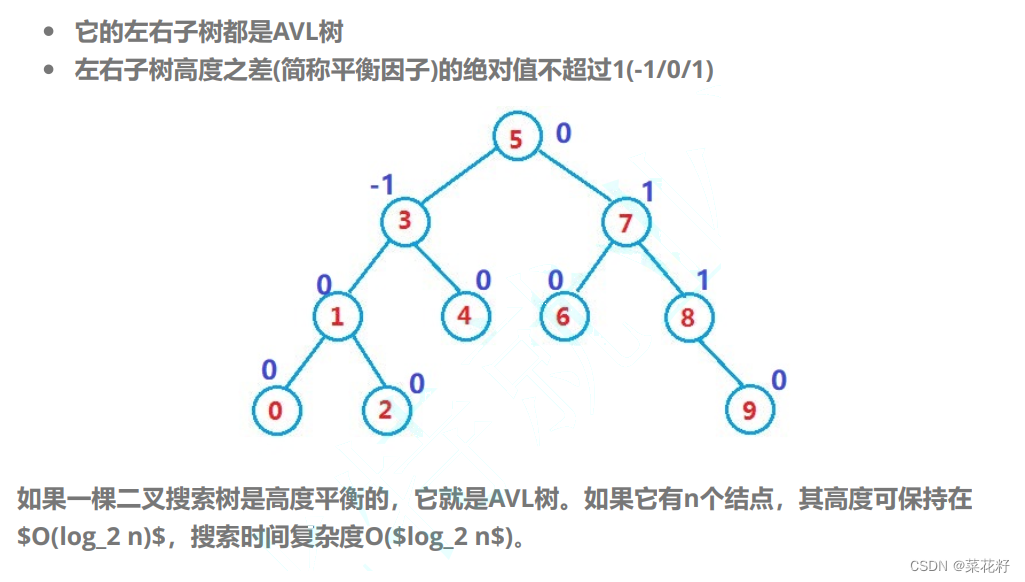
二.插入
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为两步:
- 按照二叉搜索树的方式插入新节点
- 调整节点的平衡因子
1.搜索二叉树
2.平衡因子
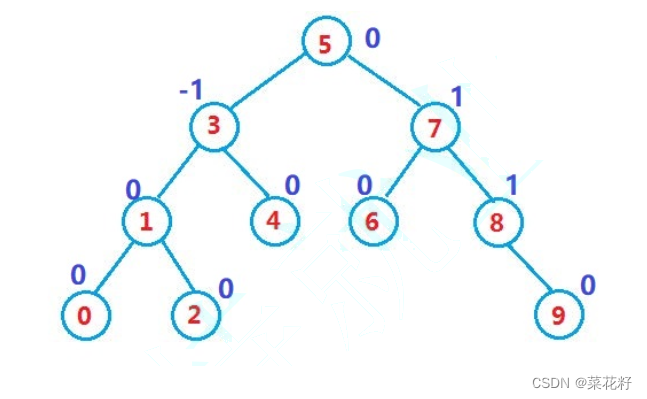
一颗树如何插入会影响节点的平衡因子呢?(平衡因子是右节点减去左节点)
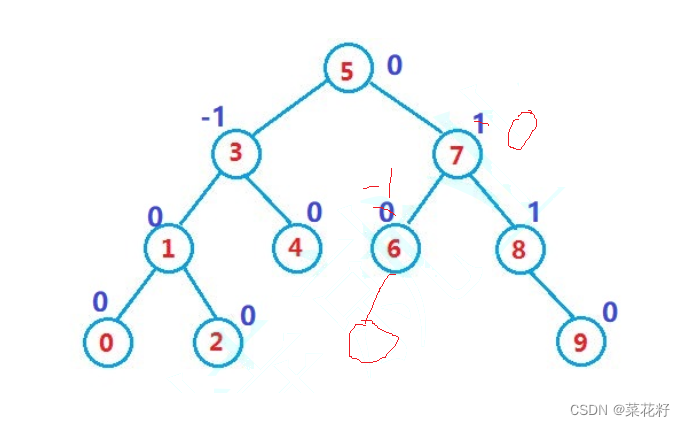
如果我们插在6的左边,那么6的平衡因子减一,同理7的左子树高度加一,那么7的平衡因子减一,再继续向上5的右子树的最高高度并没有发生改变,所以5的平衡因子不发生改变。
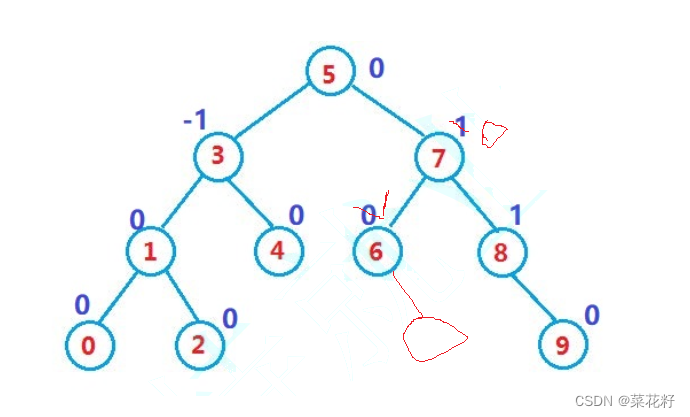
同理,插在6的右边,6的平衡因子加一,7的平衡因子减一。

如果插在9的右边,那么8的平衡因子就会变为2,说明此树不平衡。
总结:
1.新镇在左,parent平衡因子减减。
2.新增在右,parent平衡因子加加。
3.如果更新后的parent平衡因子为0,说明parent所在的树的高度不变,不会再影响祖先,不用再继续更新了。
4如果更新后parent的平衡因子为1或者-1,那么就需要继续向上更新。
5.如果更新后,parent平衡因子为2或-2,说明该树不平衡,对parent所在的子树进行旋转。
三.旋转
1.更新平衡因子
由上面分析可以知道更新结束的条件是平衡因子为0或者更新到根节点。
首先在每个节点里加入平衡因子

接着在插入的同时更新平衡因子

2.旋转
旋转要保持的要求:
1.旋转后也是搜索二叉树。
2.变成平衡树并且降低树的高度。
如果在一棵原本是平衡的AVL树中插入一个新节点,可能造成不平衡,此时必须调整树的结构,使之平衡化。根据节点插入位置的不同,AVL树的旋转分为四种:
1.左单旋
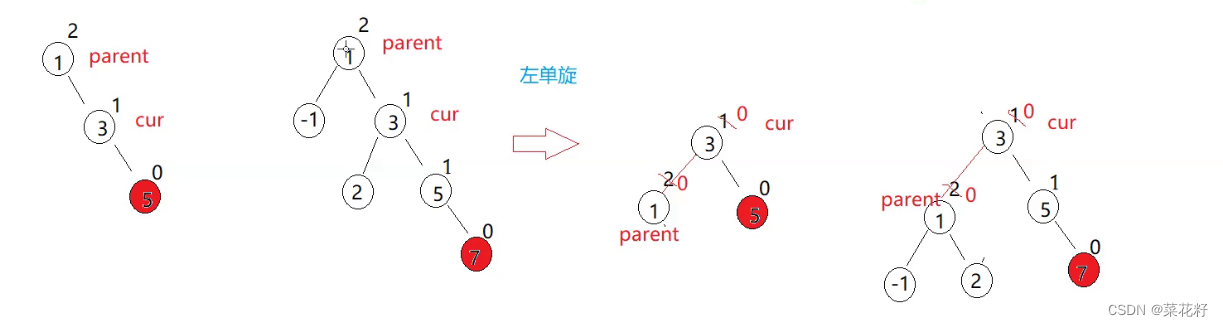

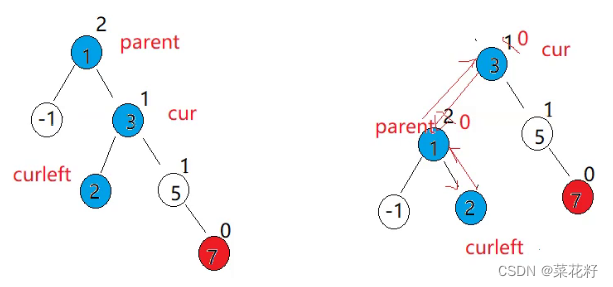
通过观察我们可以发现,我们其实只需要移动蓝色的节点就可以实现左旋。我们将这三个节点分别记录,然后修改它们的内部属性即可。

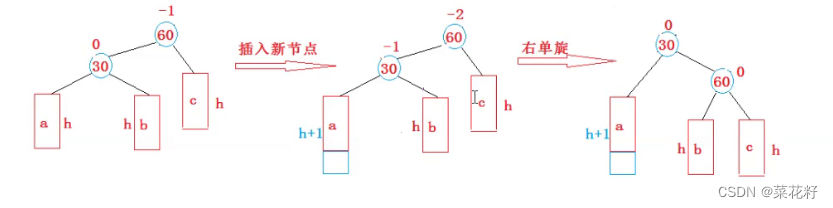
2.右单旋

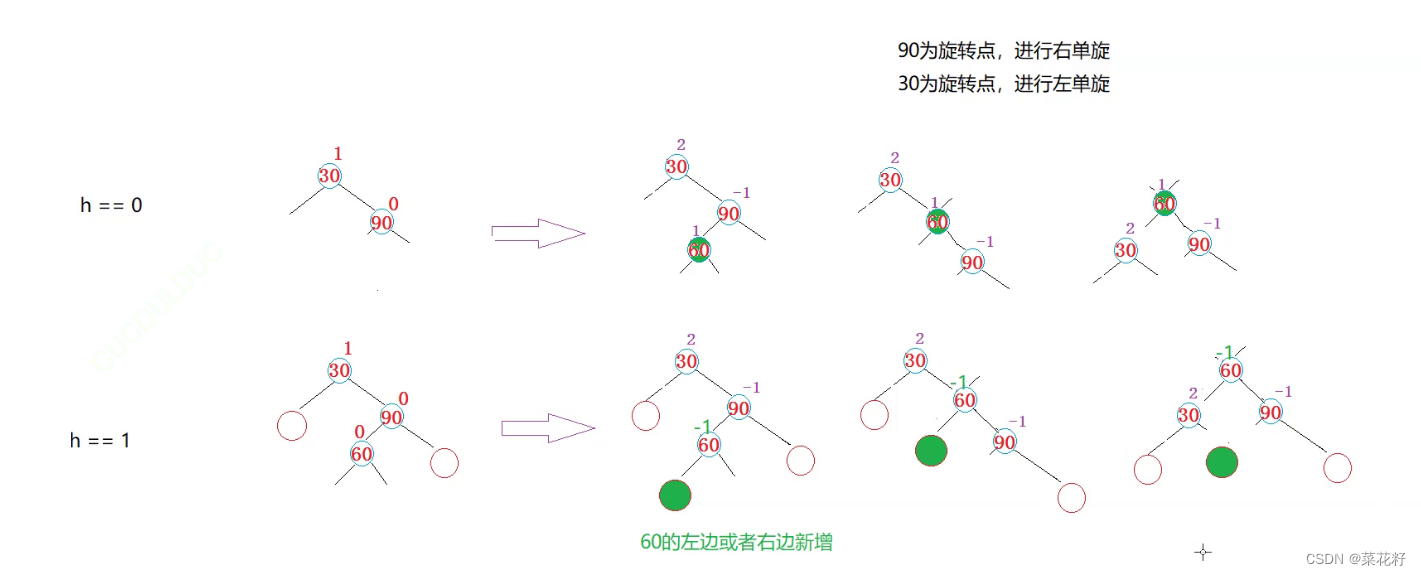
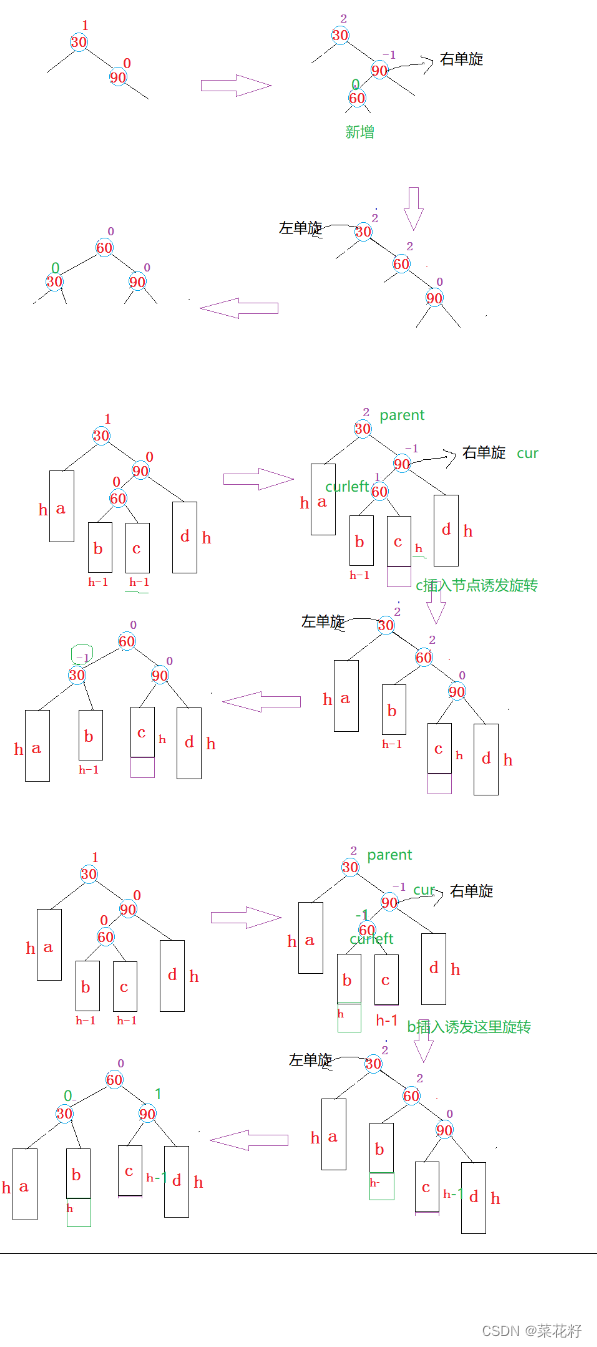
3.先右旋再左旋
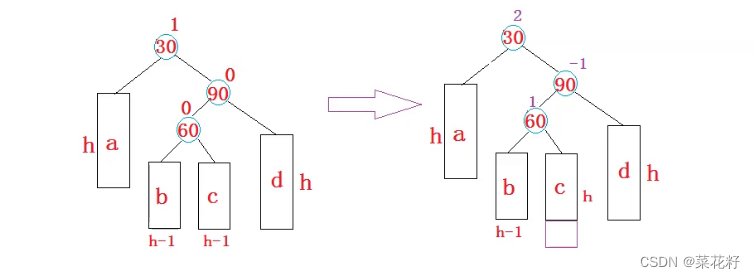
这里的旋转并不难,直接复用就可以.

困难的部分是如何调控平衡因子,插入的位置不同,平衡因子也不同分三种情况讨论。

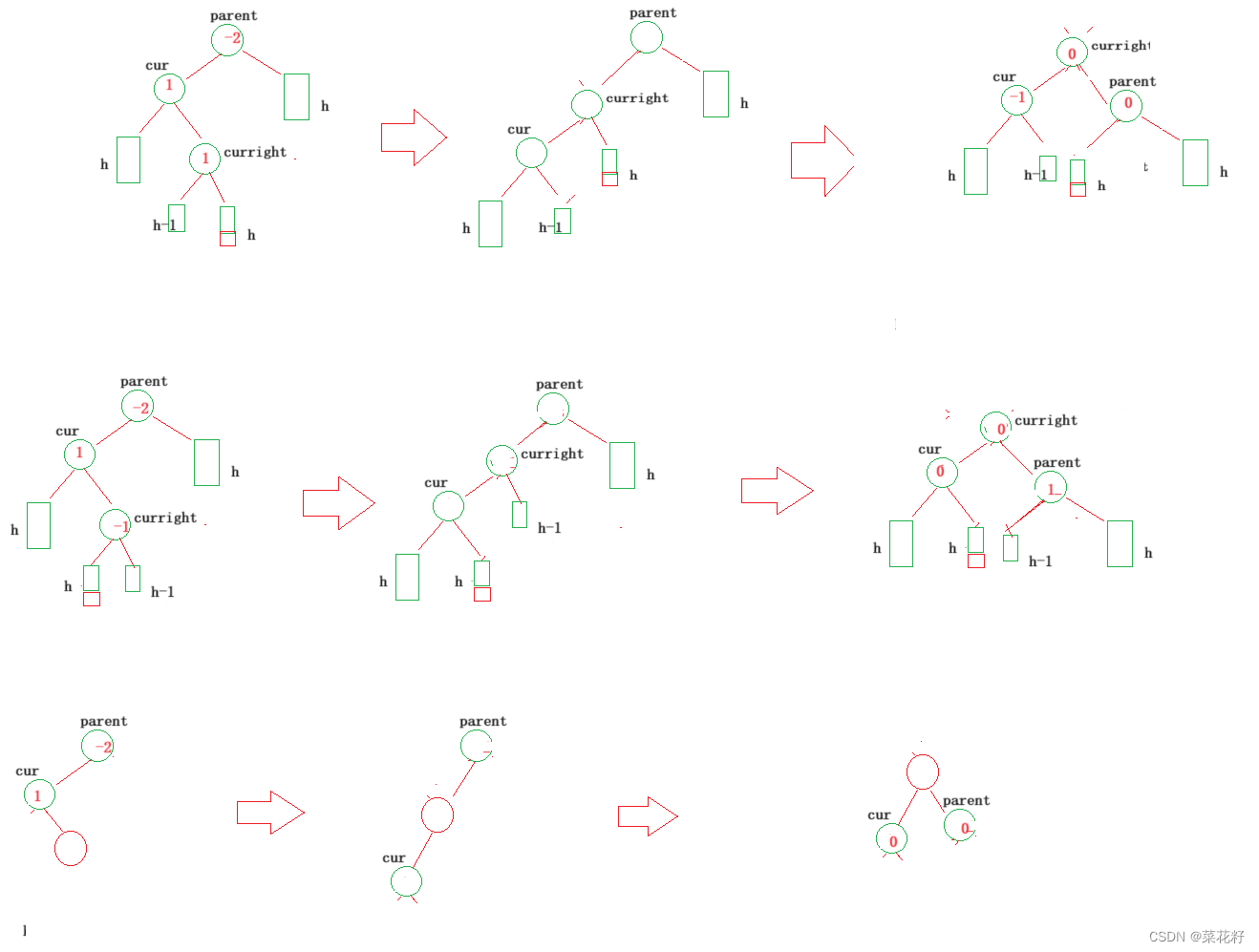
4.先左旋再右旋
同理,左右旋与上文一样,需要分三种情况来讨论。

四.完整代码
测试
#include"KVL.h"
#include<vector>int main()
{AVLTree<int,int> t;srand(time(0));vector<int>a;for (int i = 0; i < 100; i++)a.push_back(rand());for (auto x : a)t.Insert(make_pair(x,x));t.Print();
}
树
#include<iostream>
#include<assert.h>
using namespace std;template<class K,class V>
struct KVLTreeNode
{pair<K, V>_kv;KVLTreeNode<K, V>* _left;KVLTreeNode<K, V>* _right;KVLTreeNode<K, V>* _parent;int _bf;//平衡因子KVLTreeNode(const pair<K,V>&kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};template<class K,class V>
class AVLTree
{
public:typedef KVLTreeNode<K,V> Node;bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = _root;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}elsereturn false;}cur = new Node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}//控制平衡while (parent){if (cur == parent->_left){parent->_bf--;}else // if (cur == parent->_right){parent->_bf++;}if (parent->_bf == 0){// 更新结束break;}else if (parent->_bf == 1 || parent->_bf == -1){// 继续往上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){// 子树不平衡了,需要左旋转if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}//右旋转else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}//先左单旋再右旋转else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}//先右单选再左单旋else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}break;}else{assert(false);}}return true;}void RotateL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;Node* ppnode = parent->_parent;//记录父节点的父节点//父节点的右孩子变成curleftparent->_right = curleft;if(curleft)//细节注意curleft为空时不能操作curleft->_parent = parent;//父节点变为cur的左孩子cur->_left = parent;parent->_parent = cur;//如果原来父节点是根节点if (parent == _root){_root = cur;cur->_parent = nullptr;}else//如果不是根节点判断它应该是左儿子还是右儿子{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;}void RotateR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;Node* pphead = parent->_parent;//父节点到cur右边cur->_right=parent;parent->_parent = cur;//父节点的左孩子变成currightparent->_left = curright;if (curright)curright->_parent = parent;//cur的父节点变为原来父节点的父节点if (pphead)//如果不是根节点{if (pphead->_left == parent)pphead->_left = cur;elsepphead->_right = cur;cur->_parent = pphead;}else{_root = cur;cur->_parent = nullptr;}parent->_bf = cur->_bf = 0;}void RotateRL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->_bf;RotateR(parent->_right);RotateL(parent);//第一种情况if (bf == 0){parent->_bf = cur->_bf = 0;}//第二种情况else if (bf == 1){parent->_bf = -1, cur->_bf = 0, curleft->_bf = 0;}//第三种情况else if(bf==-1){cur->_bf = 1, curleft->_bf = 0, parent->_bf = 0;}//其他情况错误else{assert(false);}}void RotateLR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){parent->_bf = cur->_bf = 0;}else if (bf == 1){parent->_bf = curright->_bf = 0, cur->_bf = -1;}else if (bf == -1){parent->_bf = 1, cur->_bf = curright->_bf = 0;}else{assert(false);}}void Print(){Print(_root);}void Print(Node* root){if (root == nullptr) return;Print(root->_left);cout << root->_kv.second << ' ';Print(root->_right);}
private:Node* _root=nullptr;
};
相关文章:

【C++进阶】:AVL树(平衡因子)
AVL树 一.概念二.插入1.搜索二叉树2.平衡因子 三.旋转1.更新平衡因子2.旋转1.左单旋2.右单旋3.先右旋再左旋4.先左旋再右旋 四.完整代码 一.概念 二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元…...
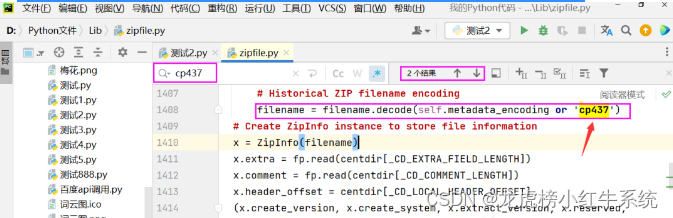
Python教程33:关于在使用zipfile模块,出现中文乱码的解决办法
zipfile是Python标准库中的一个模块,zipfile里有两个class, 分别是ZipFile和ZipInfo,用来创建和读取zip文件,而ZipInfo是存储的zip文件的每个文件的信息的。ZIP文件是一种常见的存档文件格式,它可以将多个文件和目录压缩为一个文件…...
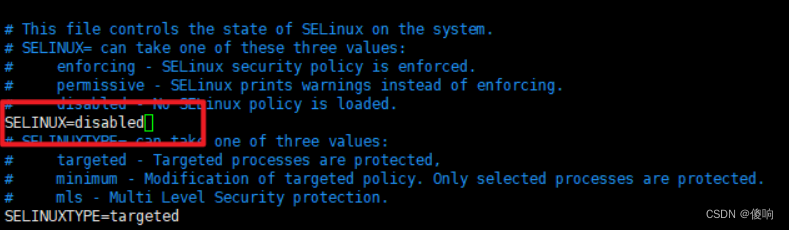
【疑难杂症】使用xshell连接云服务器连接不上
目录 【1】使用xshell连接云服务器连接不上 【1.1】解决方法一 【1.2】解决方法二 【1】使用xshell连接云服务器连接不上 Centos7使用xshell连接提示"ssh服务器拒绝了密码 请再试一次"。 问题如图所示,新安装了一台Centos7服务器,使用ssh连…...

Qt MinGW / MSVC
MinGW/MSVC的关系 MinGW / MSVC.dll / .lib / .a 的关系 MinGW / MSVC Qt 中有两种方式编译:一种是MinGW ,另一种MSVC,是两种不同的编译器。 MinGW(Minimalist GNUfor Windows),它是一个可自由使用和自由发布的Windows特定头文件…...

【数学建模】数据预处理
为什么需要数据预处理 数学建模是将实际问题转化为数学模型来解决的过程,而数据预处理是数学建模中非常重要的一步。以下是为什么要进行数据预处理的几个原因: 数据质量:原始数据往往存在噪声、异常值、缺失值等问题,这些问题会对…...
VMware 安装 黑群晖7.1.1-42962 DS918+
本例的用的文件 1、ARPL 1.0beat 引导文件 vmdk格式: https://download.csdn.net/download/mshxuyi/88309308 2、DS918_42962.pat:https://download.csdn.net/download/mshxuyi/88309383 一、引导文件 1、创建一个虚拟机 2、下一步,选稍后…...
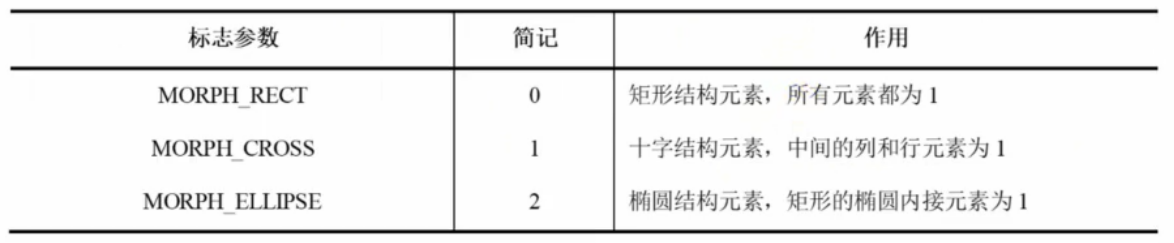
OpenCV(二十九):图像腐蚀
1.图像腐蚀原理 腐蚀操作的原理是将一个结构元素(也称为核或模板)在图像上滑动,并将其与图像中对应位置的像素进行比较。如果结构元素的所有像素与图像中对应位置的像素都匹配,那么该位置的像素值保持不变。如果结构元素的任何一个…...
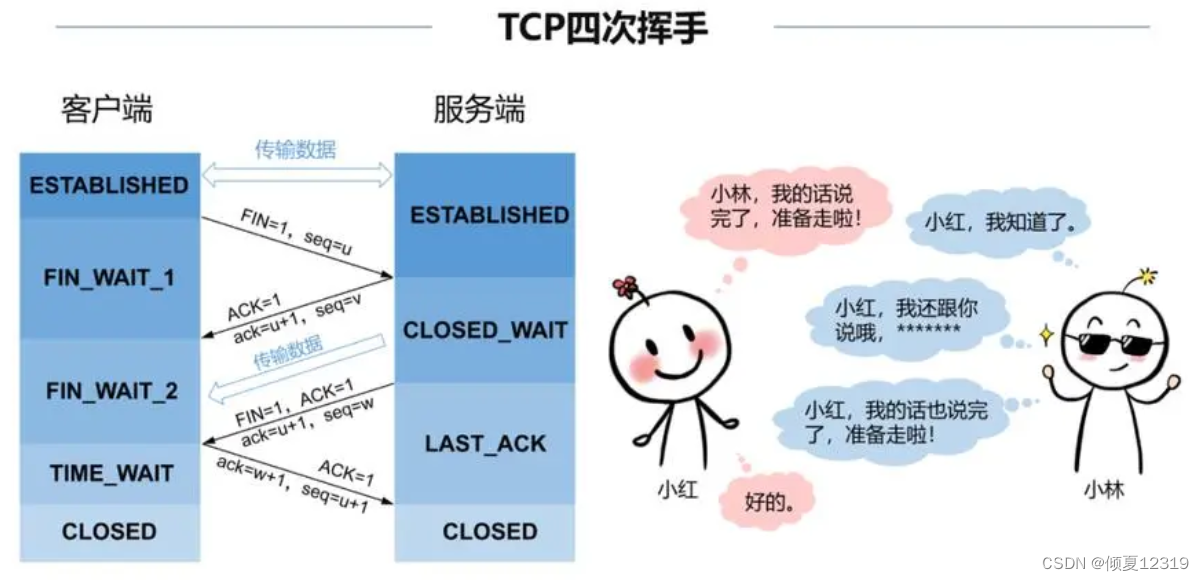
【网络知识点】三次握手和四次挥手
文章目录 一、三次握手二、四次挥手 一、三次握手 三次握手的原理如下: 客户端向服务器发送一个SYN(同步)包,其中包含一个随机生成的初始序列号(ISN)。 服务器收到SYN包后,会发送一个SYNACK&…...

CSS整理
目录 CSS中的& 弹性(display:flex)布局 flex的对齐方式 justify-content align-items flex-wrap 弹性盒换行 flex:1 flex属性 flex-grow:项目的放大比例 flex-shrink:收缩 flex-basis:初始值ÿ…...

OpenCV 06(图像的基本变换)
一、图像的基本变换 1.1 图像的放大与缩小 - resize(src, dsize, dst, fx, fy, interpolation) - src: 要缩放的图片 - dsize: 缩放之后的图片大小, 元组和列表表示均可. - dst: 可选参数, 缩放之后的输出图片 - fx, fy: x轴和y轴的缩放比, 即宽度和高度的缩放比. - …...

Java 中的日期时间总结
前言 大家好,我是 god23bin,在日常开发中,我们经常需要处理日期和时间,日期和时间可以说是一定会用到的,现在总结下 Java 中日期与时间的基本概念与一些常用的用法。 基本概念 日期(年月日,某…...
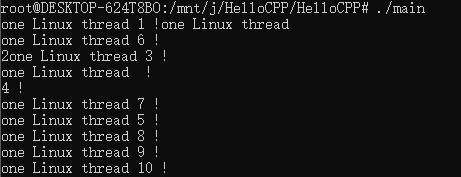
创建10个线程并发执行(STL/Windows/Linux)
C并发编程入门 目录 STL 写法 #include <thread> #include <iostream> using namespace std;void thread_fun(int arg) {cout << "one STL thread " << arg << " !" << endl; }int main(void) {int thread_count 1…...

三、创建各个展示模块组件
简介 在文件 components 中创建轮播模块组件,引入App.vue展示。欢迎访问个人的简历网站预览效果 本章涉及修改与新增的文件:First.vue、Second.vue、Third.vue、Fourth.vue、Fifth.vue、App.vue、vite-env.d.ts、assets 一、修改vite-env.d.ts文件 /// <reference type…...

推荐一款程序员截图神器!
快来看一下程序员必备的一款截图工具 今天就来和大家说一下作为程序员必备截图神器,几乎每一个程序员都会设置开机自启,因为这个截图功能太太太好用了!!!只要你在键盘上按下F1就可以轻松截取整个屏幕,然后…...

无涯教程-JavaScript - IMCSC函数
描述 IMCSC函数以x yi或x yj文本格式返回复数的余割。 复数的余割定义为正弦的倒数。即 余割(z) 1 /正弦(z) 语法 IMCSC (inumber)争论 Argument描述Required/OptionalInumberA complex number for which you want the cosecant.Required Notes Excel中的复数只是简单…...

Ubuntu22.04 LTS 显卡相关命令
第一部分查看驱显卡信息 一、查看显卡型号 # -i表示不区分大小写 lspci | grep -i nvidia # 必须安装好nvidia驱动 nvidia-smi -L 二、查看显卡驱动版本 cat /proc/driver/nvidia/version 三、查看CUDA、cuDNN版本 # 或者 nvcc -V(两个显示的版本一致…...

《TCP/IP网络编程》阅读笔记--基于 TCP 的半关闭
目录 1--基于TCP的半关闭 1-1--TCP单方面完全断开的问题 1-2--shutdown()函数 1-3--半关闭的必要性 2--基于半关闭的文件传输程序 1--基于TCP的半关闭 1-1--TCP单方面完全断开的问题 Linux 系统中的 close 函数会将 TCP Socket 的连接完全断开,这意味着不能收…...

Rust的模块化
Rust的模块化要从Rust的入口文件谈起。 Rust的程序的入口文件有两个 如果程序类型是可执行应用,入口文件是main.rs;如果程序类型是库,入口文件是lib.rs; 入口文件中,必须声明本地模块,否则编译器在编译过…...

vmware设置桥接模式后ip设置
网络连接方式设置 找到虚拟机里机器的网络设置 左边是宿主机,右边是虚拟机,按照这个设置就可以上网了(IP指定一个没有占用的值,子网掩码和网关设置成一样的)就可以联网了。 over~~...
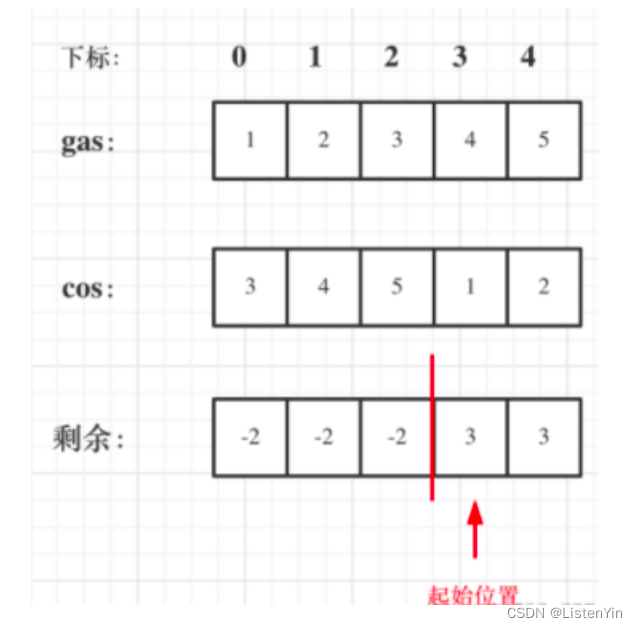
算法通关村第十七关:白银挑战-贪心高频问题
白银挑战-贪心高频问题 1. 区间问题 所有的区间问题,参考下面这张图 1.1 判断区间是否重叠 LeetCode252 https://leetcode.cn/problems/meeting-rooms/ 思路分析 因为一个人在同一时刻只能参加一个会议,因此题目的本质是判断是否存在重叠区间 将区…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
