16-数据结构-图的存储结构
简介:主要为图的顺序存储和链式存储。其中顺序存储即邻接矩阵的画法以及代码,邻接矩阵又分为有权图和无权图,区别就是有数据的地方填权值,无数据的地方可以填0或者∞,而有权图和无权图,又细分为有向图和无向图。无向图为对称矩阵,因为没有方向可言,出度入度一样。而有向图则有区分,对了,邻接矩阵横着看,是出度,竖着看是入度。链式存储中则包含邻接表、十字链表和邻接多重表,其中邻接表,有向图和无向图都可以,而十字链表是其邻接表有向图的优化,可以同时计算入度和出度,而邻接多重表,是邻接表无向图的优化,可以节约一半的边数空间,由原来的顶点数+2*总边数,变为了顶点数+总边数。
目录
一、顺序存储-邻接矩阵
1.1-简介
1.2-代码
1.3-运行结果
二、链式存储-邻接表
2.1邻接表
2.1.1.代码
2.2十字链表
2.2.1代码
2.3邻接多重表
2.3.1代码:
一、顺序存储-邻接矩阵
1.1-简介
图嘛,自然是包括了顶点和边。而邻接矩阵则是通过数组的形式,表示图。
其中需要一个一维数组,用来存储顶点的信息——顶点即一个单位像学生1,学生2之类的。
还需要一个二维数组,就是邻接矩阵,来存储顶点之间的关系;其次,则是记录,图中顶点数和边的总数。
我代码的思路,是自己想的,从创建到可以运行,如果遇到简单的,我后期再来改。
思路:
- 先初始化图,给图输入想要的顶点数和边数。其次初始化一维数组和二维数组。
- 创建以及输入数据,先给顶点的信息,输入顶点数组中。随后是进行判断,看是有向图还是无向图。(这里面默认是无权图)(有权图,只不过又多了一组需要手动输入的数字)。
- 无向图,是对称矩阵,输入想要的边的关系,即1与2,则邻接矩阵对应的直接改为1,表示两个点之间相连,同时更新对称位置也为1.
- 有向图。则是更新一个就行,另一个不更新。
1.2-代码
#include <stdio.h>
#define Max 10
#include <string.h>
//图的顺序存储_邻接矩阵
typedef struct
{char vertex[Max]; //存放顶点的一维数组 int edge[Max][Max]; //表示顶点之间关系的二维数组; int vertex_num; //顶点数 int edge_num; //边数 }MGragh;
//初始化邻接矩阵
void InitMGragh(MGragh *a)
{printf("添加几个顶点\n");int x;scanf("%d",&x); //赋值 a->vertex_num=x;printf("有多少条边\n"); int c; scanf("%d",&c);//赋值 a->edge_num=c;//初始化邻接矩阵存储边信息的二维数组 a->edge[Max][Max];int p,q;for(p=0;p<a->vertex_num;p++){for(q=0;q<a->vertex_num;q++){a->edge[p][q]=0;}} //初始化,顶点数组 a->vertex[a->vertex_num]='0';
}
//打印邻接矩阵
void PrintMGragh(MGragh *a)
{int p,q;for(p=0;p<a->vertex_num;p++){for(q=0;q<a->vertex_num;q++){printf("%d ",a->edge[p][q]);}printf("\n");}
}
void Creat_MGragh(MGragh *a)
{printf("图的顶点数%d\n",a->vertex_num);int i=0;printf("请加顶点到顶点数组\n"); for(i=0;i<a->vertex_num;i++){ printf("i=%d\n",i);char x;x=getchar();char k;//由于单个字符输入,回车也在输入序列中,因此还需要一个变量,来吃掉回车 k=getchar();a->vertex[i]=x;}printf("您想弄成无向图还是有向图,1为无向图,2为有向图\n");int text;scanf("%d",&text);if(text == 1){printf("请添加顶点间关系\n"); int w=0;while(w!=2){printf("哪个顶点和哪个顶点之间有联系\n");int d1,d2;scanf("%d %d",&d1,&d2);a->edge[d1-1][d2-1]=1;a->edge[d2-1][d1-1]=1;printf("是否还需要继续添加,是填1,否填2\n");scanf("%d",&w); } }else{printf("请添加顶点间关系\n"); int w=0;while(w!=2){int d1,d2;printf("从哪个顶点到哪个顶点\n");scanf("%d %d",&d1,&d2);a->edge[d1-1][d2-1]=1;printf("是否还需要继续添加,是填1,否填2\n");scanf("%d",&w); }}
}int main()
{MGragh a;//初始化图 InitMGragh(&a);//创建邻接矩阵图 Creat_MGragh(&a); //打印邻接矩阵 PrintMGragh(&a);return 0;} 1.3-运行结果
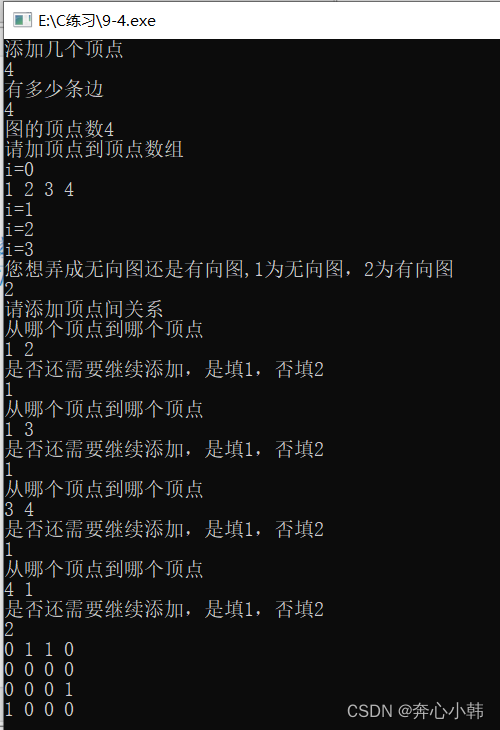
二、链式存储-邻接表
2.1邻接表
简介:邻接表,实际上主要为一个顶点表后面串着相应的边表。在记录总的边数和顶点数。
为链式存储。它适用于稀疏图,方便计算出度,只需要找到相应的顶点,然后通过该顶点的单链表,往后遍历串就行。但入度则需要遍历每个顶点单链表。
无向图,有向图都可以。有向图,每个顶点传一个方向的,要么都弄出度,要么都弄入度。所以它所需要的空间为O(顶点数+总边数);而无向图,则是与该顶点相连的,都穿起来,因此所需要的存储空间为O(顶点数+2*总边数)。
2.1.1.代码
边表ArcNode:包括该点下标和下一个指针域。
//边表
typedef struct ArcNode
{int NodeName;struct ArcNode *next;}ArcNode; 顶点表:存储图的各个顶点,每个顶点后面实际上是对应的从他出发的出度的单链表。
//顶点表
typedef struct
{int data;//顶点内容 ArcNode* first; //顶点标的链的头指针 }VNode;邻接表:最后才是邻接表,即只需要通过顶点表,就可访问其各个顶点的出度。
//创建邻接表,包含顶点表和边表,以及边数和顶点数的记录
typedef struct
{VNode vertice[vertice_num];//顶点表,每个顶点标中的数据,串成一个对应的链 int vexnum;//顶点数 int edgenum;//边数
}ALGragh; 由于实现的话,以我目前的水平,感觉有点麻烦,需要遍历每个顶点,每个顶点还需要创建边表结点,还需要给每个顶点单链表,形成,目前没思路,写到中间卡壳了,以后熟练了,再来补实现
2.2十字链表
简介:十字链表仅适用于有向图,为了弥补邻接表中有向图只能计算单向的度。
多了一些入度的信息。先给邻接表的形式,出度画出来。随后再找顶点表中各个顶点的入度,入0的入度,从0出发,看边表中,哪个终点为0,则连起来,没有则置为空。
十字链表仍然是通过顶点表,即可遍历相应顶点的出度链和入度链,即可直到相应顶点的出度和入度。
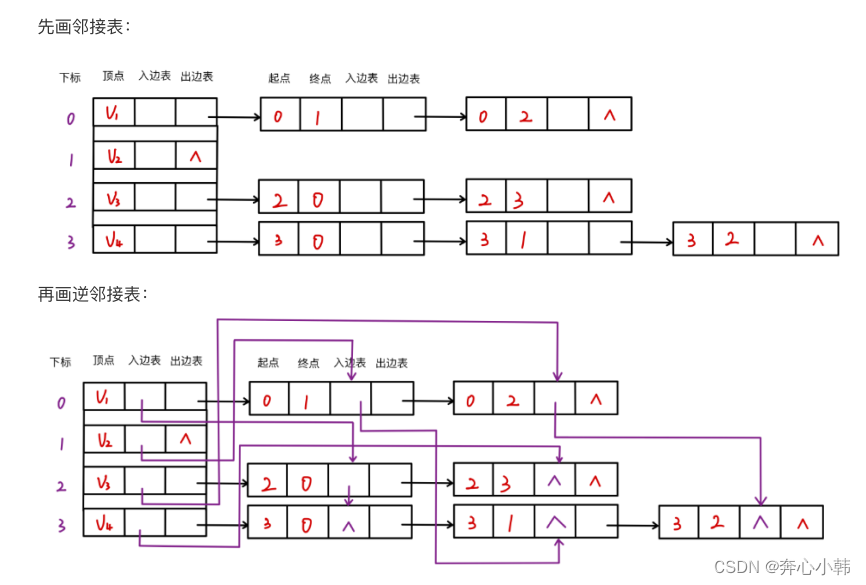
2.2.1代码
//边表
typedef struct ArcNode
{int tailvex,headvex;//弧尾tail弧头head 弧尾(起点)->弧头(终点) struct ArcNode *hlink,*tlink;//指针域,即出度指针域为弧头,入读指针域为弧尾,先连接弧头指针域,出度、再连接弧尾指针域 char info;//存储信息的指针
}ArcNode;
//顶点表
typedef struct VNode
{AreNode *firstin,*firstout;//出度入读头指针 int data;//顶点信息 }VNode;
//十字链表
typedef struct GLGraph
{VNode xlist[vertice_num];//顶点表 int vexnum,edgenum;//顶点数和边数 }GLGraph; 2.3邻接多重表
简介:邻接多重表仅适用于无向图,是邻接表中无向图,的优化,邻接表中无向图,会重复多连,2*总边数,而邻接多重表节约,为E。
画法:先画出顶点表和边表,边表中为与最左边顶点表中顶点相关的顶点,即边,为边的起点和边的终点,并有两个相关的指针域。第一步,先标记好相应的数值,自上而下画,下方顶点,若有重复的边,则不画。
//强连通机构的例题——不想自己画了,偷个懒
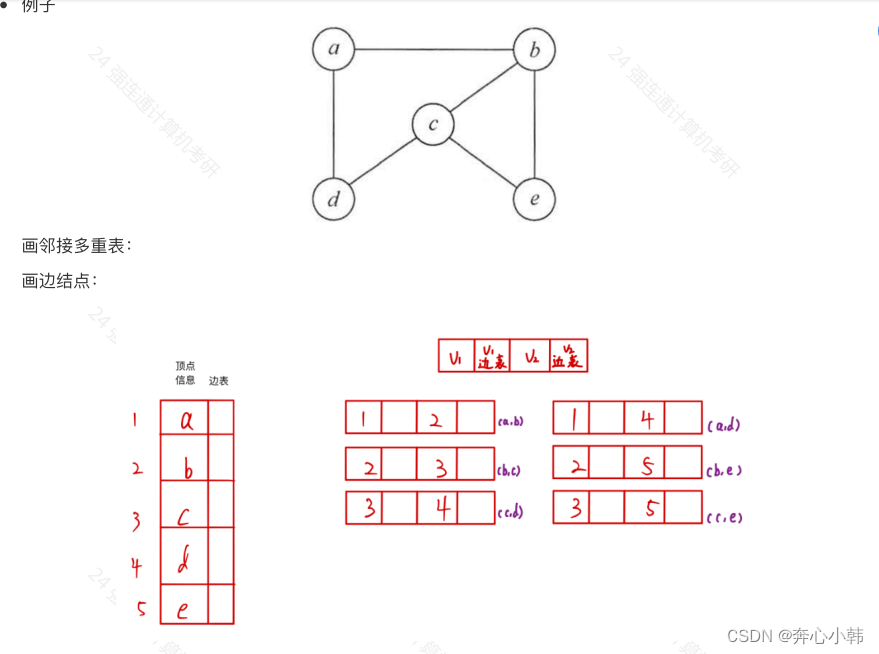
第二步,串链,由左边顶点表中的顶点出发,找右边边表中,与该顶点相同的指针域,连接上即可,如b的下标是2,从b出发,找右边边表中2的指针域。2的指针域第一行有一个,第二行有两个,给这三个串上即可。

2.3.1代码:
//邻接多重表-无向图
//边表
typedef struct AreNode
{int mark; //标记是否串过int ivex,jvex;//表示弧的两个顶点struct AreNode *ilink,*jlink;char info;//其他信息
}AreNode;
//顶点表
typedef struct VNode
{int data;//顶点信息 AreNode *first;//指向边表中第一个挨着该顶点的结点 }VNode;
//邻接多重表
typedef struct AMLGraph
{VNode xlist[vertice_num];//顶点表 int vexnum,edgenum;//总边数和总结点数
}AMLGraph;
相关文章:

16-数据结构-图的存储结构
简介:主要为图的顺序存储和链式存储。其中顺序存储即邻接矩阵的画法以及代码,邻接矩阵又分为有权图和无权图,区别就是有数据的地方填权值,无数据的地方可以填0或者∞,而有权图和无权图,又细分为有向图和无向…...
)
递推算法及常见示例(C++、Python实现)
递推算法及常见示例(C、Python实现) 递推算法是一种用若干步可重复运算来描述复杂问题的方法,它是一种序列计算中的常用算法。通常是通过计算前面的一些项来得出序列中的指定项的值。其思想是把一个复杂的庞大的计算过程转化为简单过程的多次…...
vscode调试程序设置
主要设置和json内容如下: cpp_properties.json内容: {"configurations": [ //C intellisense插件需要这个文件,主要是用于函数变量等符号的只能解析{"name": "Win32","includePath": ["${work…...
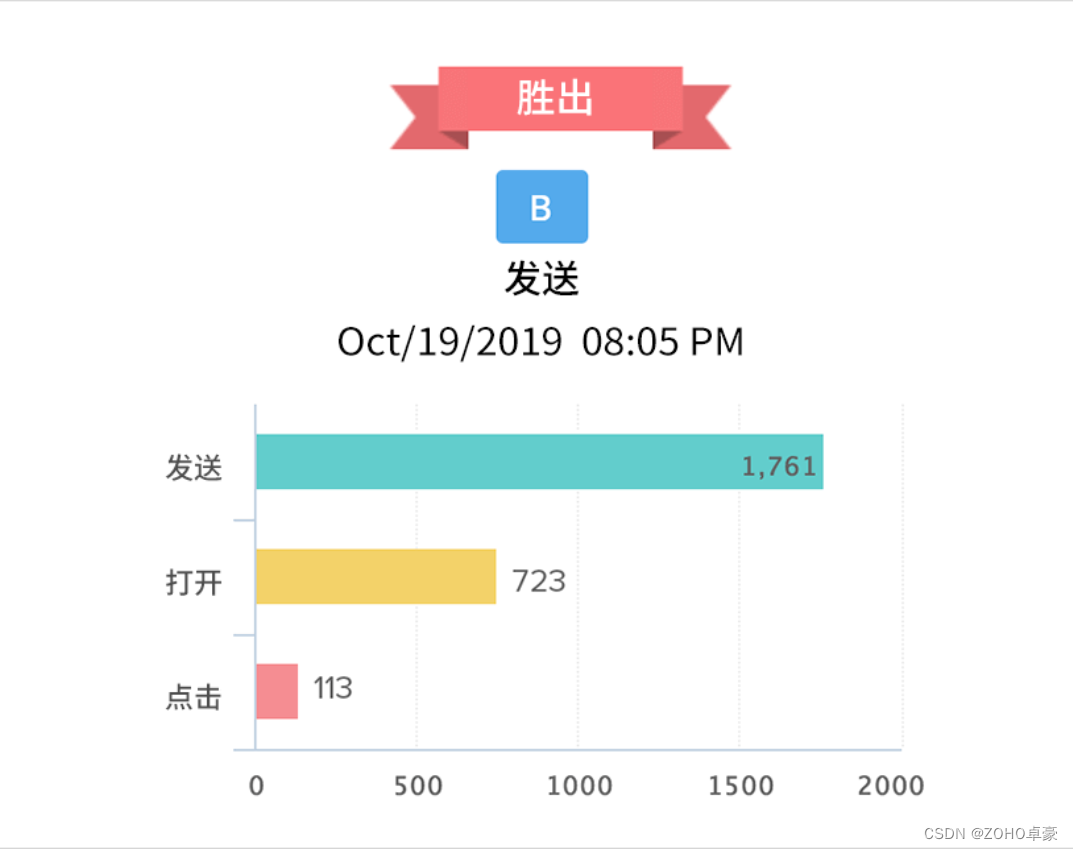
电商邮件营销攻略:教你如何有效运营邮件营销策略!
作为一种领先的营销渠道,电子邮件营销已被电子商务公司作为推动客户参与度、促进销售和提高ROI的不可或缺的方式。在这篇文章中,我们将深入探讨电子商务公司为什么要做EDM邮件营销?以及电商公司怎么做邮件营销? 一、电子商务公司…...
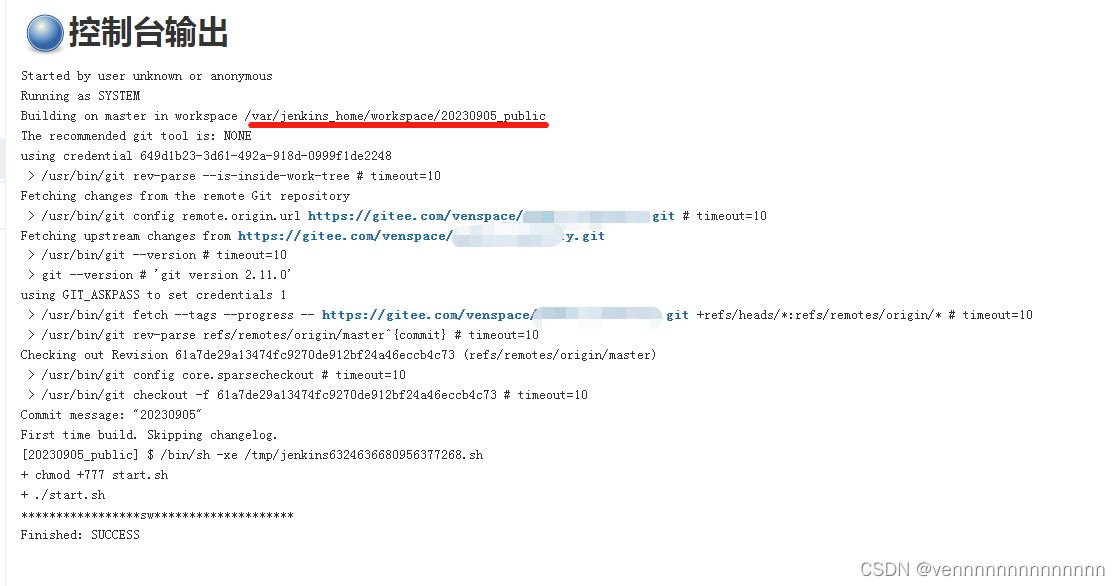
centos+jenkins+pycharm
思路:架构 一. 在centos上搭建jenkins环境 二. pycharm与gitee建立连接 三. 访问jenkins,添加任务 3.1 添加一个自由风格的任务 3.2 添加git项目路径及访问git的账号和密码 3.3 执行start.sh脚本 四. 浏览器访问jenkins执行任务...
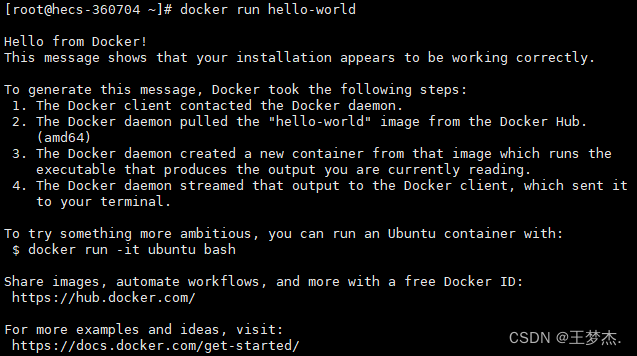
Linux-Centos7安装Docker
文章目录 一、前言二、Docker安装1、Docker及系统版本2、Docker的自动化安装3、Docker手动安装3.1、卸载Docker(可选)3.2、设置源仓库3.3、Docker安装3.4、Docker启动3.5、验证是否安装成功3.5.1、拉取镜像3.5.2、查看镜像3.5.3、运行镜像 3.6、删除Dock…...

前端Vue入门-day06-路由进阶
(创作不易,感谢有你,你的支持,就是我前行的最大动力,如果看完对你有帮助,请留下您的足迹) 目录 路由的封装抽离 声明式导航 导航链接 两个类名 自定义高亮类名 跳转传参 1. 查询参数传参 2. 动态…...

数据库服务器是什么意思?数据库服务器有哪些?
数据库服务器是什么意思?现在市场上有很多的服务器的类型,比如数据库服务器,但是很多人对数据库服务器是什么意思?数据库服务器有哪些并不是很熟悉,那么,聚名企服为您详解一下。 一:数据库服务器是什么意思 数据库服…...

配电网智能软开关(sop)规划模型matlab
目录 1 主要内容 2 部分程序 3 程序结果 1 主要内容 该程序参考文献《基于改进灵敏度分析的有源配电网智能软开关优化配置》,采用二阶锥算法,以改进的IEEE33节点配电系统模型作为分析对象,以联络开关位置作为sop安装备选位置,以…...

Qt 常用函数
设置编码 #if (QT_VERSION < QT_VERSION_CHECK(5,0,0)) #if _MSC_VERQTextCodec *codec QTextCodec::codecForName("gbk"); #elseQTextCodec *codec QTextCodec::codecForName("utf-8"); #endifQTextCodec::setCodecForLocale(codec);QTextCodec::se…...

UMA 2 - Unity Multipurpose Avatar☀️六.Advanced Occlusion高级遮挡功能解决皮肤服饰穿模
文章目录 🟥 本节功能效果展示🟧 基础项目配置🟨 本节项目配置🟩 配置MeshHideAsset1️⃣ 创建MeshHideAsset2️⃣ 配置SlotDataAsset3️⃣ 配置遮挡信息🟦 将 MeshHideAsset 配置到 Recipe🟥 本节功能效果展示 未遮挡前的穿模问题: 遮挡后效果:...
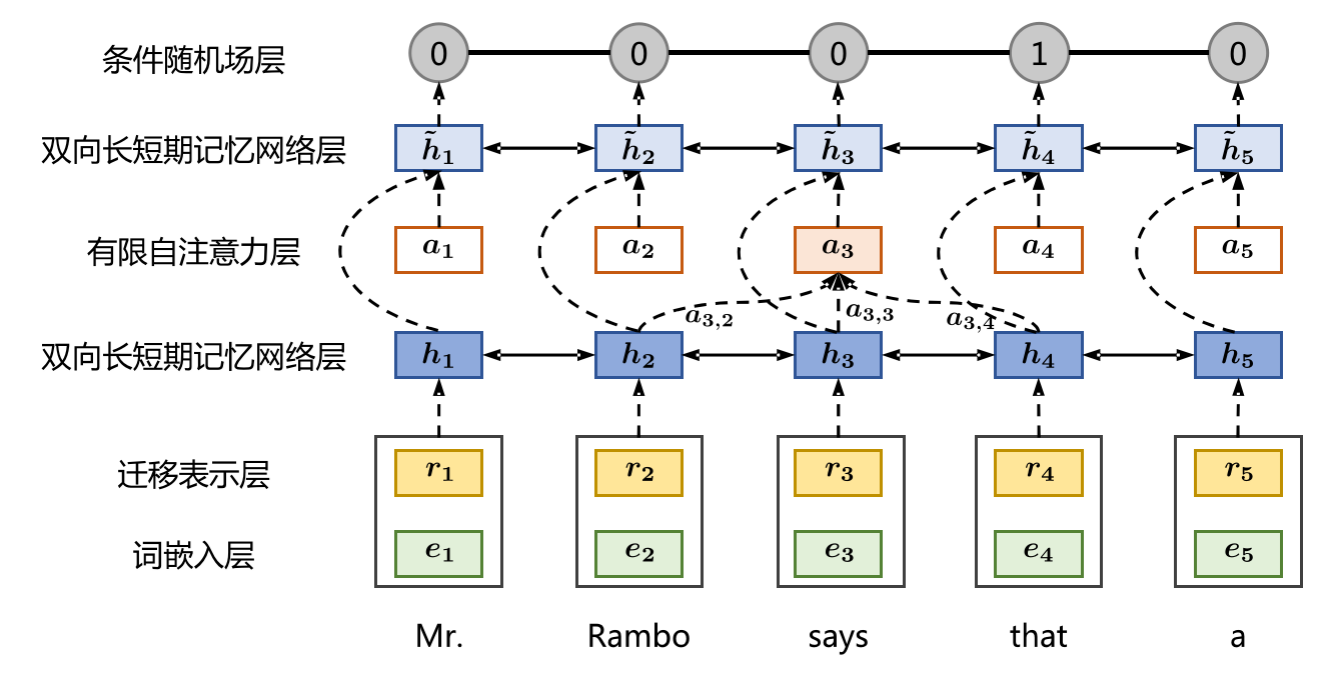
深度解析自然语言处理之篇章分析
在本文中,我们深入探讨了篇章分析的概念及其在自然语言处理(NLP)领域中的研究主题,以及两种先进的话语分割方法:基于词汇句法树的统计模型和基于BiLSTM-CRF的神经网络模型。 关注TechLead,分享AI全维度知识…...
、文件系统(os/ shutil/json/pickle/openpyxl/xlrd))
Python3.11教程3:模块和包(pip/conda)、文件系统(os/ shutil/json/pickle/openpyxl/xlrd)
文章目录 七、模块和包7.1 模块7.1.1 模块搜索路径7.1.2 PYTHONPATH和sys.path7.1.2 模块的导入和常见错误7.1.3 模块的缓存机制7.1.4 __name__ 和 __main__ 函数 7.2 标准库7.3 包7.3.1 创建包7.3.2 导入包7.3.3 pip包管理器7.3.4 conda 7.4 如何组织和管理大型项目中的模块与…...
)
shell 脚本工具(三剑客)
第一个:awk awk 是一种强大的文本处理工具和编程语言,最初由 Alfred Aho、Peter Weinberger 和 Brian Kernighan 在20世纪70年代早期创建。awk 的名称来自于这三位创造者的姓氏的首字母。它在 Unix 和类 Unix 操作系统中广泛使用,用于处理、…...
基于微信小程序的智能垃圾分类回收系统,附源码、教程
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 1 简介 视频演示地址: 基于微信小程序的智能垃圾分类回收系统,可作为毕业设计 小…...

【C++进阶】:AVL树(平衡因子)
AVL树 一.概念二.插入1.搜索二叉树2.平衡因子 三.旋转1.更新平衡因子2.旋转1.左单旋2.右单旋3.先右旋再左旋4.先左旋再右旋 四.完整代码 一.概念 二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元…...
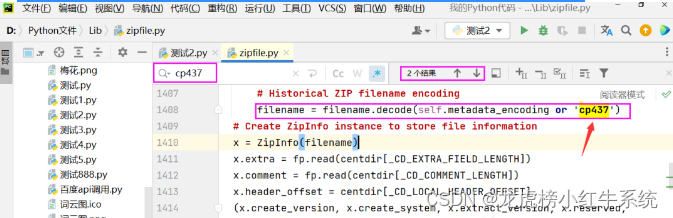
Python教程33:关于在使用zipfile模块,出现中文乱码的解决办法
zipfile是Python标准库中的一个模块,zipfile里有两个class, 分别是ZipFile和ZipInfo,用来创建和读取zip文件,而ZipInfo是存储的zip文件的每个文件的信息的。ZIP文件是一种常见的存档文件格式,它可以将多个文件和目录压缩为一个文件…...
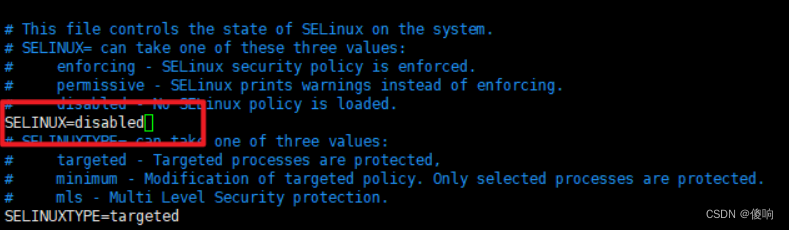
【疑难杂症】使用xshell连接云服务器连接不上
目录 【1】使用xshell连接云服务器连接不上 【1.1】解决方法一 【1.2】解决方法二 【1】使用xshell连接云服务器连接不上 Centos7使用xshell连接提示"ssh服务器拒绝了密码 请再试一次"。 问题如图所示,新安装了一台Centos7服务器,使用ssh连…...

Qt MinGW / MSVC
MinGW/MSVC的关系 MinGW / MSVC.dll / .lib / .a 的关系 MinGW / MSVC Qt 中有两种方式编译:一种是MinGW ,另一种MSVC,是两种不同的编译器。 MinGW(Minimalist GNUfor Windows),它是一个可自由使用和自由发布的Windows特定头文件…...

【数学建模】数据预处理
为什么需要数据预处理 数学建模是将实际问题转化为数学模型来解决的过程,而数据预处理是数学建模中非常重要的一步。以下是为什么要进行数据预处理的几个原因: 数据质量:原始数据往往存在噪声、异常值、缺失值等问题,这些问题会对…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...
