CRC原理介绍及STM32 CRC外设的使用
1. CRC简介
循环冗余校验(英语:Cyclic redundancy check,简称CRC),由 W. Wesley Peterson 于 1961 年首次提出的一种纠错码理论。
CRC是一种数据纠错方法,主要应用于数据通信或者数据存储的场合,用来检测或校验数据传输或者数据存储后可能出现的错误,特别是擅长检测由传输通道中的噪声引起的常见错误。
CRC是数据通信领域中最流行的一种错误检测方法,传输过程中的数据信息字段长度,以及校验码的字段长度可以任意自定义的指定,但是通信双方必须使用同一标准的CRC校验。
2. CRC模型及其相关概念
很多大佬们在研究CRC算法的时候,设计了各种CRC的算法模型,这些模型可以适用不同的校验场合,比如 CRC-16 ,CRC-32 等不同的算法模型。
一般我们在具体的项目中,要使用CRC校验的时候,首先就要选择合适的算法模型,根据选定的CRC算法模型,才能计算得到对应的CRC校验码。然后,通信双方约定好使用的CRC校验模型,才能保证校验的一致性。
下图截图自一个CRC校验码在线计算工具网站的常用的CRC算法模型:
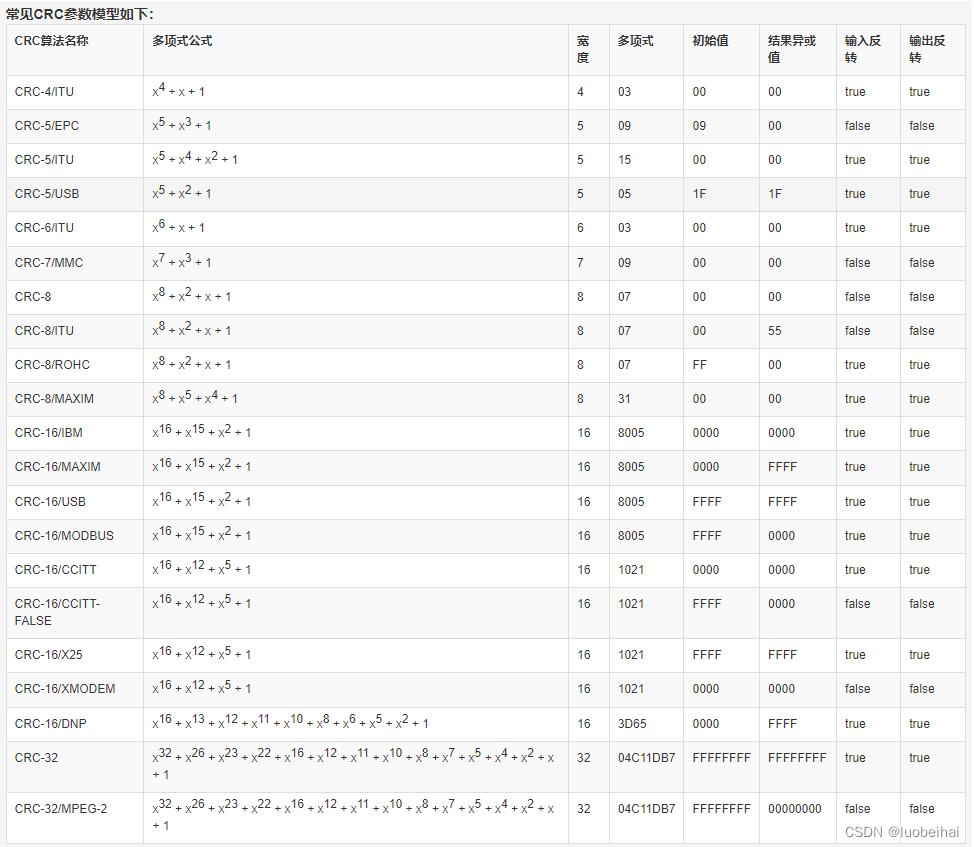
注:上面的多项式表示中,是16进制数,而且是省略了最高位的。
这些CRC算法模型中,有几个重要的组成部分,或者说计算CRC校验码时,需要知道的一些概念,如多项式公式、16进制多项式、宽度、初始值、结果异或值等等。
2.1 多项式公式
多项式公式,是CRC校验中最重要的一个概念。
对任意的二进制数都可以构造一个与其对应的二进制系数多项式公式。
比如,二进制:10011b,它对应的二进制系数多项式就是:
P ( x ) = x 4 + x + 1 P(x) = x^4 + x + 1 P(x)=x4+x+1
这个公式怎么来的呢?
# 二进制数 1 0 0 1 1
# 下标 4 3 2 1 0
# 二进制多项式 1 * X4 + 0 * X3 + 0 * X2 + 1 * X1 + 1 * X0# 所以最后得出的多项式公式就是:X4 + X + 1
成为多项式要满足的条件
- 最高位和最低位都必须是1
- 当数据在传输过程中出错时,CRC的校验码不应该是0(也就是要有余数)
- 该多项式要有最大的错误检测能力
2.2 16进制的多项式表示
一般在计算CRC校验码的时候,我们习惯使用16进制的多项式,这个16进制的多项式,是被省略了最高位 1 的。
因为前面说了,多项式的最高位和最低位,都必须是1,所以一般都会把这个多项式的最高位给省略掉(这里我也没搞懂,反正当它是一个不可描述的规定吧)。
比如前面介绍的,P(x) = X4 + X + 1 ,这个多项式公式,他对应的CRC模型就是 CRC-4/ITU ,然后它的多项式使用16进制表示就是 0x03 ,本来这个多项式应该是0x13的,但是省略了最高位,所以变成了 0x03.
2.3 位宽
位宽,指的就是CRC校验码的二进制位数。这个是和你选择的CRC模型有关的,你选择不同的CRC模型,那么CRC的多项式公式就不一样,所以对应的CRC校验码数据位宽也不一样。
比如前面介绍的多项式公式 :P(x) = X4 + X + 1 ,那么CRC的校验码位宽就是 4 个二进制位数。因为多项式的最高位为4.
2.4 CRC变体相关的概念
前面介绍的3个参数概念,是CRC模型中必须要有的概念。其他一些概念,比如初始值、输入数据反转,输出数据反转,结果值是否异或处理等,这些都属于CRC变体的处理。
如果没有特意规定的话,那么这些参数默认都是没有的,比如初始值没有规定,则默认为0。没有说明是否反转,那么一般不会对数据进行反转的操作等。
2.4.1 初始值
CRC模型中,有些模型规定CRC的初始值不是0。这个初始值,其实就是CRC校验码的计算过程中,在第一次进行异或计算时,是否有一个初始值。这个如果看C言语实现CRC计算过程就比较直观。
初始值的数据位宽和CRC校验码的位宽是一样的。
2.4.2 输出结果值异或
计算得到了CRC校验码后,如果规定了输出的结果值要进行异或的数不为0,那么最后得到CRC校验码时,还得进行结果值异或这步操作。这样才能最终得到CRC校验码
2.4.3 输入输出值反转
在一些CRC模型中,还会规定输入值与输出值是否反转。
输入值反转,就是在计算CRC校验码之前,是否对原始数据(待测数据)进行按位反转。比如:1010001,反转之后就是:1000101
输出值反转,就是最终得到的CRC结果值,是否进行反转操作。
3. 模2运算
CRC校验的计算理论源自多项式除法,它是一种二进制除法,被叫做模2除法。待检测的数据除以多项式,最终得到的余数就是CRC检验码。
模2运算,是一种二进制运算,是二进制编码理论中的运算基础。这种运算和我们以前学的四则运算的规则不同,模2运算不考虑进位、借位这些规则,它有着新的运算规则。
模2运算也有加减乘除,下面是它们的运算示例。
3.1 模2加法
加法规则:1+1=0 0+0=0 1+0=1 0+1=1
1 0 1 0
+ 1 1 0 0
-----------0 1 1 0
3.2 模2减法
减法规则:0-0=0 1-1=0 0-1=1 1-0=1
1 0 1 0
- 1 1 0 0
-----------0 1 1 0
3.3 模2乘法
乘法规则:0×0=0 0×1=0 1×0=0 1×1=1
模2乘法与普通的乘法一样的演算规则,只不过在按位相加时,是按照模2加法规则进行的。
1 0 1 1x 1 0 1----------------1 0 1 10 0 0 01 0 1 1----------------1 0 0 1 1 1
3.4 模2除法
除法规则:0÷1=0 1÷1=1
模2除法与普通的除法也是一样的演算规则,但是就是在按位相减时,是按照模2减法规则进行的。
1 1 1 0 (商)|-----------------
1 0 1 1 | 1 1 0 0 1 0 0 (被除数)1 0 1 1-----------------0 1 1 1 11 0 1 1-----------------0 1 0 0 01 0 1 1-----------------0 0 1 1 0 (最后余数)
从上面的模2运算示例可以看出一些规律:
- 模2的加减法运算结果是一样的,他和C语言的异或运算有着一样的规则。所以我们软件实现这个算法时就是使用异或实现的。
- 模2的乘除法运算,与普通的运算有着类似的演算规则。但是在乘法时乘积相加,除法时余数和除数相减,就需要安装模2加减法规则运算。
- 当余数的位数小于除数时,模2除法停止运算
- 当被除数,或者在除法进行过程中得到的部分余数,它们与除数位数一样多,那么商1,否则商0.
4. CRC校验码的计算和检测原理
4.1 CRC校验码的计算
CRC校验码的计算,其实就是模2除法的运算过程。
在计算过程中,我们首先要知道二进制多项式,这个多项式其实就是除数,而待校验的数据就是被除数,最终进行模2除法运算得到的余数,就是CRC校验码。
下面以多项式: P(x) = x^4 + x + 1 为例,该多项式对应的二进制数就是:10011 ,进行计算演示。
第一步:原始数据补充 n 个 0
假设要进行编码的原始数据为:1100110,而前面约定好了的多项式的最高位是4,所以CRC校验码的位宽就是4。所以我们先假设余数是 0000 四个0,补充在原始数据的后面,那么最终参与计算的数就是:11001100000
第二步:进行模2除法运算
1 1 0 0 1 1 0 0 0 0 0 (原始数据,后面加了4个0)1 0 0 1 1 (多项式)
----------------------------------0 1 0 1 0 11 0 0 1 1
----------------------------------0 0 1 1 0 0 01 0 0 1 1
----------------------------------0 1 0 1 1 01 0 0 1 1
----------------------------------0 0 1 0 1 0 01 0 0 1 1
----------------------------------0 0 1 1 1
当最终计算得到的余数的位数,小于多项式的位数的时候,运算停止,然后得到的余数就是CRC的校验码。
在数据传输过程中,就会把这个校验码放到原始数据的后面,组成一个新的数:11001100111 ,发送给接收方。当接收方在接收到这个数据后,就会进行CRC校验,也就是除以约定好的多项式,如果最终的余数为0,那么说明接收方接收的数据正确。
4.2 CRC校验检测原理
上面介绍计算CRC校验码说了,我们首先要约定好收发双方的除数,这个除数其实就是多项式。进行校验检测的大概过程就是:
(1) 先约定好收发双方选择的CRC多项式 多项式,这个多项式其实就是计算过程中的除数。
(2) 在待校验的数据(可看作是发送方的数据)后面加上 n 个0,这个 n 是多少取决于你所选择的多 项式。比如你选择的多项式是:P(x) = x^4 + x + 1 。那么CRC检验码的位宽就是4,也就是说你要补4个0
(3) 对待校验数据进行模2除法运算,得出的余数就是CRC校验值。
(4) 然后把CRC检验码添加到待检验数据的末尾。这样就组成了一个新的数了,这个是是添加了CRC校验码的。然后把这个新的数发送给接收方。
(5) 接收方,把接收到的数据,也进行模2除法的计算过程,如果余数为0,那么接收正确,如果不为0,那么数据在传输过程中出错。
5. CRC校验的软件代码
我们前面一直说了,CRC校验码的计算,其实就是模2除法。然后模2除法,对应到C言语中来,那就可以通过异或和移位操作来实现。
所以,CRC算法的软件实现,主要就是异或和移位操作实现的。实现方法主要有两种: 按位校验和查表。按位校验法消耗更多的CPU算力,查表法则消耗更多的RAM空间。
不同的CRC模型,按位校验法有不同的算法实现,主要是CRC变体的处理,初始值的不同等。不过也是有相似的规律,大致的代码实现过程是相同的。
网上也有大佬们已经实现了的各种CRC模型的算法库,我这里给出一个网上比较全的CRC算法库,如果有我们需要软件实现CRC校验的话,可以去移植过来。
LibCRC官网:https://www.libcrc.org/
LibCRC github仓库:https://github.com/lammertb/libcrc
还有下面这个,主要是按位校验法实现的CRC代码库:
https://github.com/whik/crc-lib-c
5.1 软件实现的代码片段
下面是摘抄自 wiki 的其中一种按位校验方式实现的CRC算法,大致的代码思路如下:
function crc(byte array string[1..len], int len)
{remainderPolynomial := 0 // 多项式的初始值// 这里有一个流行的变体对剩余多项式进行补充,比如输入数据是否进行反转for i from 1 to len{// 这个步骤要看不同的CRC模型,有不同的处理。n是CRC的位宽,如果小于8的位宽,不用移位remainderPolynomial := remainderPolynomial xor (string[i] * (n << 8))for j from 1 to 8 { // 每个字节是 8 bitif (remainderPolynomial最高位为1){remainderPolynomial := (remainderPolynomial << 1) xor generatorPolynomial(多项式)}else {remainderPolynomial := (remainderPolynomial << 1)}}}// 这里有一个流行的变体对剩余多项式进行补充,比如是否对CRC校验码进行输出反转,进行异或处理return remainderPolynomial
}
基本上,按位校验法的CRC代码实现,就是上面的这个套路。
5.2 CRC32-MPEG-2 模型的代码实现
这里给出一个 CRC32-MPEG-2 这个模型的CRC代码实现。
uint32_t crc32_mpeg2(uint8_t data[], uint32_t length)
{uint32_t crc = 0xffffffff;for (int i = 0; i < length; i++){crc = crc ^ (data[i] << 24);for (int j = 0; j < 8; j++){if ( crc & 0x80000000 ){crc = (crc << 1) ^ 0x04C11DB7;}else{crc = crc << 1;}}}return crc;
}
上面这个模型,其实也是一些MCU硬件的CRC实现的模型,比如STM32、APM32的MCU。
6. STM32的CRC外设使用
STM32 的 CRC 外设,使用的算法模型是 CRC32-MPEG-2 。
STM32 CRC 的数据位宽为 32 位,十六进制多项式为 0x4C11DB7, INIT=0xFFFFFFFF, REFIN=false,REFOUT=false, XOROUT=0x00000000
对于 STM32 CRC外设的使用也很简单,在使能了CRC外设时钟之后,就可以调用SDK(我使用的是STM32的标准固件库函数)提供的CRC计算函数,然后就可以得到对应数据的CRC校验码了。
下面以 STM32F407 为例,使用CRC外设计算校验码的代码:
static uint32_t CRC_Test_Buff[2] = {0x01, 0x02};int main(void)
{uint32_t uCRCValue = 0;/* Enable CRC Periph clock */RCC_AHB1PeriphClockCmd(RCC_AHB1Periph_CRC, ENABLE);/* Resets the CRC Data register */CRC_ResetDR();/* Calculate the 32-bit CRC value */uCRCValue = CRC_CalcBlockCRC(CRC_Test_Buff, sizeof(CRC_Test_Buff) / 4);printf("CalculateBlockCRC = 0x%08X \r\n", uCRCValue);while (1){}
}
其中要注意的是,CRC_CalcBlockCRC 这个函数提供的输入数据类型是 32 位 的。
运行上面的代码输出结果如下:
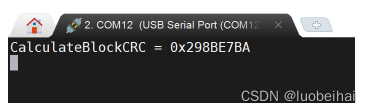
然后我们到CRC校验码的在线计算工具,验证下我们使用STM32 CRC外设计算得到的校验码是否一致。计算结果如下图:
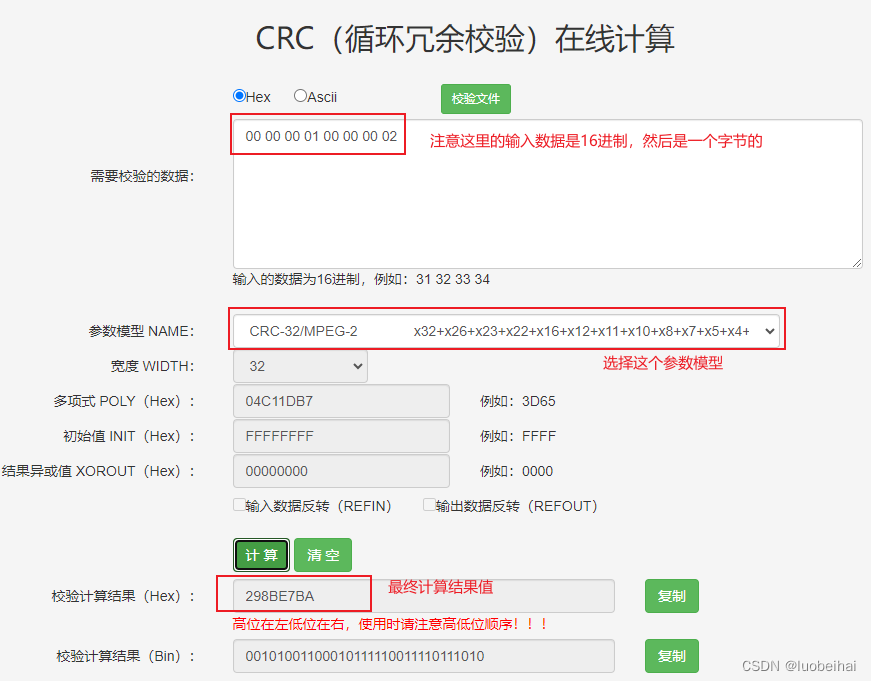
我们要选择的参数模型是, CRC32-MPEG-2 这个,输入的数据类型要注意一下是16进制,而且是1个字节。这个和我们STM32的代码是4个字节的数据不同,要自己拆分为1个字节输入到那个框框里面。
然后最终的计算结果是:0x298BE7BA ,这个值和我们使用 STM32 外设计算出来的结果是一致的。
相关文章:

CRC原理介绍及STM32 CRC外设的使用
1. CRC简介 循环冗余校验(英语:Cyclic redundancy check,简称CRC),由 W. Wesley Peterson 于 1961 年首次提出的一种纠错码理论。 CRC是一种数据纠错方法,主要应用于数据通信或者数据存储的场合ÿ…...
Python 操作 Word
上次给大家介绍了 Python 如何操作 Excel ,是不是感觉还挺有趣的,今天为大家再介绍下,用 Python 如何操作 Word ,这个可能跟数据处理关系不大,用的也不多,不过可以先了解下都能实现什么功能,以备…...
-退出--孤儿进程)
Linux--进程创建(fork)-退出--孤儿进程
进程创建: ①使用fork函数创建一个进程,创建的新进程被称为子进程。 #include <unistd.h>//头文件 pid_t fork(void); fork函数调用成功,返回两次: 返回值为0, 代表当前进程为子进程; 返回值为非负数…...

LeetCode 热题 HOT 100:链表专题
LeetCode 热题 HOT 100:https://leetcode.cn/problem-list/2cktkvj/ 文章目录 2. 两数相加19. 删除链表的倒数第 N 个结点21. 合并两个有序链表23. 合并 K 个升序链表141. 环形链表142. 环形链表 II148. 排序链表160. 相交链表206. 反转链表234. 回文链表 2. 两数相…...
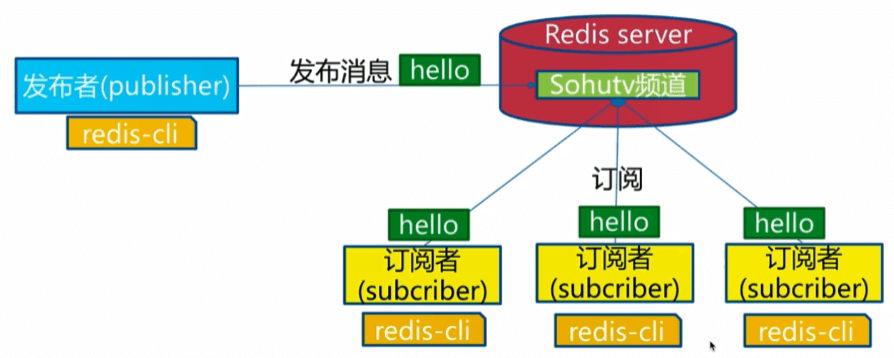
Redis发布订阅
在现代的软件开发中,数据存储和管理是至关重要的一环。Redis,作为一个开源的、内存中的数据结构存储系统,以其出色的性能和灵活的数据结构,赢得了开发者们的广泛喜爱。它不仅可以用作数据库,还可以用作缓存和消息代理。…...
在Windows操作系统上安装PostgreSQL数据库
在Windows操作系统上安装PostgreSQL数据库 一、在Windows操作系统上安装PostgreSQL数据库 一、在Windows操作系统上安装PostgreSQL数据库 点击 PostgreSQL可跳转至PostGreSQL的官方下载地址。 (1) (2)选择安装的目录ÿ…...

【云原生】Kubeadmin部署Kubernetes集群
目录 编辑 一、环境准备 1.2调整内核参数 二、所有节点部署docker 三、所有节点安装kubeadm,kubelet和kubectl 3.1定义kubernetes源 3.2开机自启kubelet 四、部署K8S集群 4.1查看初始化需要的镜像 4.2在 master 节点上传 v1.20.11.zip 压缩包至 /opt 目录…...

Java中wait和notify详解
线程的调度是无序的,随机的,但是也是有一定的需求场景,希望能够有序执行,join算是一种控制顺序的方式(功能有限)——》一个线程执行完,才能执行另一个线程! 本文主要讲解的…...

算法竞赛个人注意事项
浅浅记录一下自己在算法竞赛中的注意事项。 数据类 注意看数大小,数学库中的函数尽量加上 * 1.0,转成double,防止整型溢出。,int型相乘如果可能溢出,乘 * 1LL。 数据范围大于1e6,注意用快读。 浮点数输…...

ClickHouse和Doris超大数据集存储
文章目录 一. ClickHouse1. 性能2. 可靠性3. 可扩展性4. 支持SQL和复杂查询5. 适用场景 二. Doris1. 性能2. 可靠性3. 易用性4. 适用场景 三. ClickHouse和Doris的比较1. 架构2. 性能3. 可靠性4. 易用性5. 适用场景 四. 总结 ClickHouse和Doris是两种流行的超大数据集存储方案。…...
02-Flask-对象初始化参数
对象初始化参数 前言对象初始化参数import_namestatic_url_pathstatic_foldertemplate_floder 前言 本篇来学习Flask中对象初始化参数 对象初始化参数 import_name Flask程序所在的包(模块),传__name__就可以 _name_ 是一个标识 Python 模块的名字的变量&#x…...
第5篇 vue的通信框架axios和ui框架-element-ui以及node.js
一 axios的使用 1.1 介绍以及作用 axios是独立于vue的一个项目,基于promise用于浏览器和node.js的http客户端。 在浏览器中可以帮助我们完成 ajax请求的发送在node.js中可以向远程接口发送请求 1.2 案例使用axios实现前后端数据交互 1.后端代码 2.前端代码 &…...
RabbitMQ 知识点解读
1、AMQP 协议 1.1、AMQP 生产者的流转过程 当客户端与Broker 建立连接的时候,会调用factory .newConnection 方法,这个方法会进一步封装成Protocol Header 0-9-1 的报文头发送给Broker ,以此通知Broker 本次交互采用的是AMQPO-9-1 协议&…...
SimVODIS++: Neural Semantic Visual Odometry in Dynamic Environments 论文阅读
论文信息 题目:SimVODIS: Neural Semantic Visual Odometry in Dynamic Environments 作者:Ue-Hwan Kim , Se-Ho Kim , and Jong-Hwan Kim , Fellow, IEEE 时间:2022 来源: IEEE ROBOTICS AND AUTOMATION LETTERS(RAL…...

7.Xaml Image控件
1.运行图片 2.运行源码 a.xaml源码 <!--Source="/th.gif" 图像源--><!--Stretch="Fill" 填充模式--><Image x:Name...
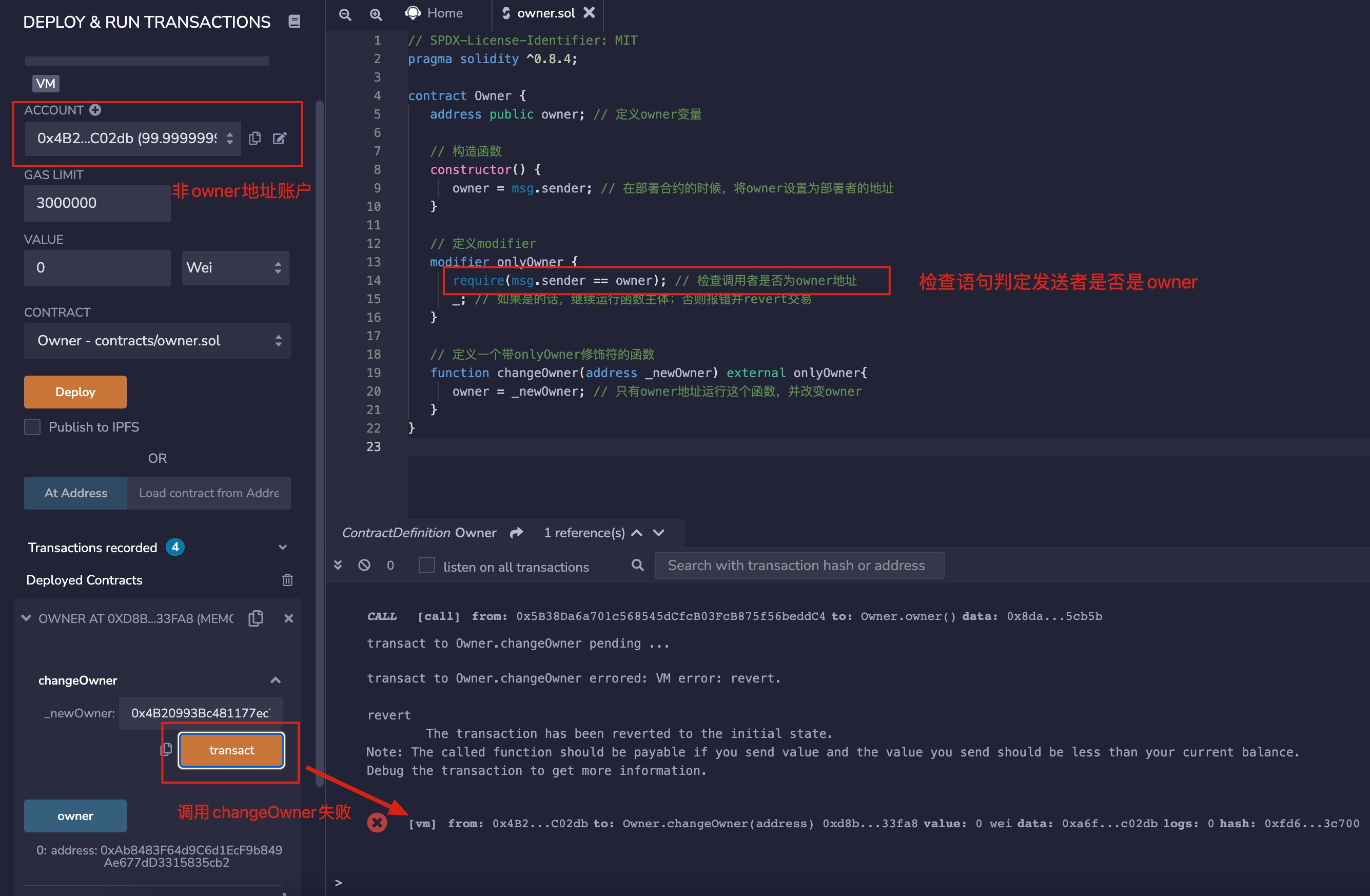
Solidity 小白教程:11. 构造函数和修饰器
Solidity 小白教程:11. 构造函数和修饰器 这一讲,我们将用合约权限控制(Ownable)的例子介绍solidity语言中构造函数(constructor)和独有的修饰器(modifier)。 构造函数 构造函数&…...
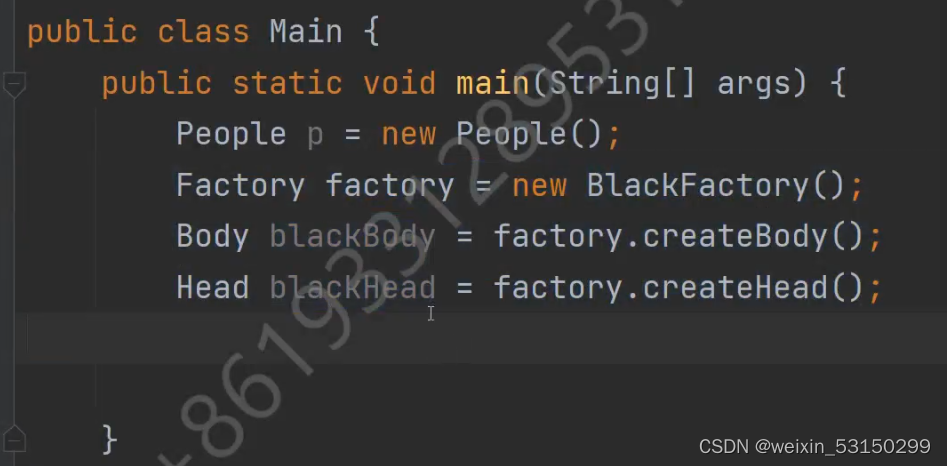
静态工厂模式,抽象工厂模式,建造者模式
静态工厂模式 ublic class FruitFactory {public static Fruit getFruit(String name) {Fruit fnull;switch (name){case "APPLE":{fnew Apple();}case "BANANA":{fnew Banana();}default :{System.out.println("Unknown Fruit");}}return f;} …...
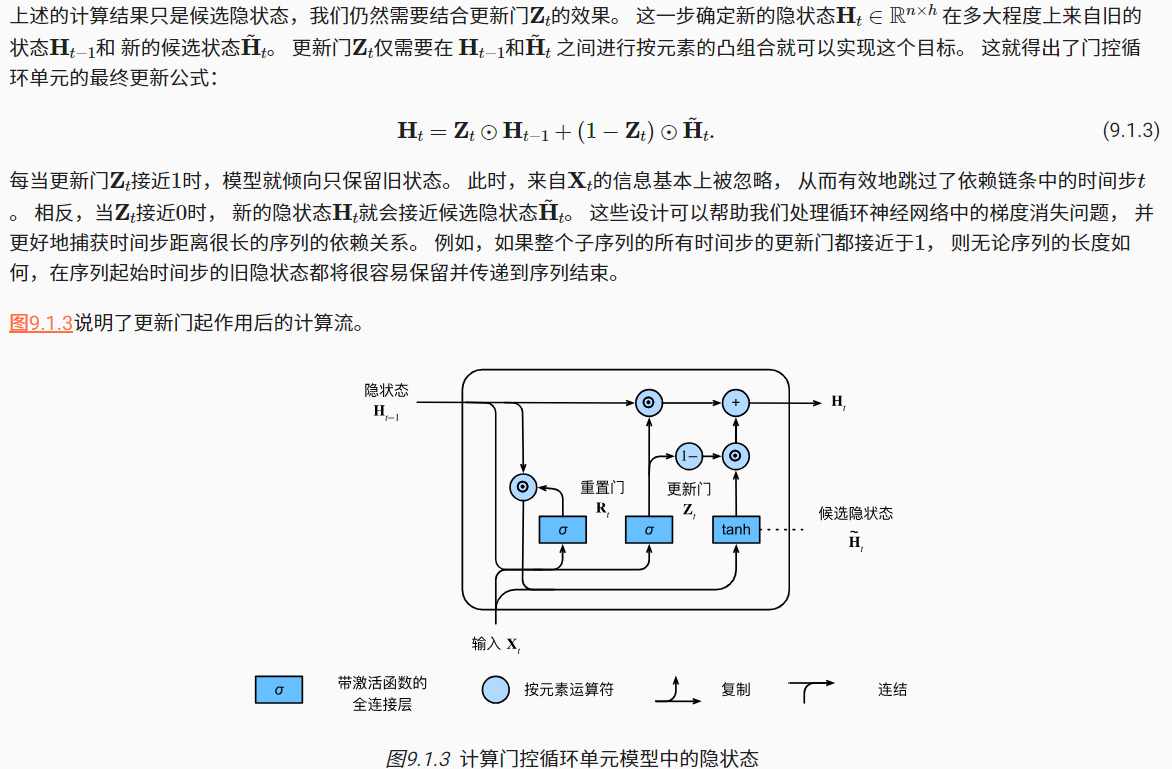
【动手学深度学习笔记】--门控循环单元GRU
文章目录 门控循环单元GRU1.门控隐状态1.1重置门和更新门1.2候选隐状态1.3隐状态 2.从零开始实现2.1读取数据2.2初始化模型参数2.3定义模型2.4训练与预测 3.简洁实现 门控循环单元GRU 学习视频:门控循环单元(GRU)【动手学深度学习v2】 官方…...
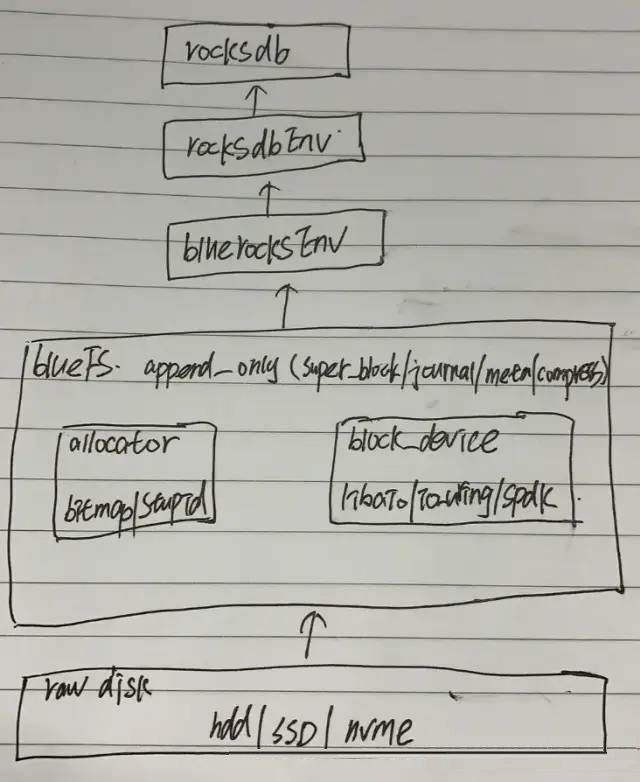
浅析linux异步io框架 io_uring
前言 Linux内核5.1支持了新的异步IO框架iouring,由Block IO大神也即Fio作者Jens Axboe开发,意在提供一套公用的网络和磁盘异步IO,不过io_uring目前在磁盘方面要比网络方面更加成熟。 目录 背景简介 io_uring 系统API liburing 高级特性…...

访问者模式的一个使用案例——文档格式转换
访问者模式的一个使用案例——文档格式转换 假设我们在开发一个文档编辑器,它支持多种不同的文档元素(如段落、图片、表格等),现在我们需要添加一个功能——将文档导出为 HTML 或 Markdown 格式。 这就是一个典型的访问者模式的…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...
