【EKF】EKF原理
原理简述
卡尔曼滤波可以在线性模型,误差为高斯模型的情况下,对目标状态得出很好的估计效果,但如果系统存在非线性的因素,其效果就没有那么好了。比较典型的非线性函数关系包括平方关系,对数关系,指数关系,三角函数关系等。
对于非线性系统的问题,比较常用的方法是将非线性的部分进行线性化处理,其中,EKF 就是对非线性系统进行线性化,使用泰勒展开式,略去二阶及以上项(数据较小),得到一个近似的线性化模型,然后应用卡尔曼滤波完成估计。
EKF与KF的对比推导
卡尔曼滤波的五个公式:

泰勒展开式为:
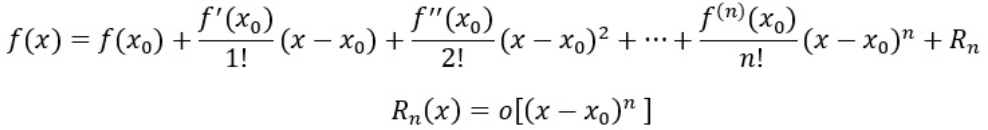
在 EKF 中,泰勒展开式只保留前两项,即:
f(x) ≈ f(x0) + f'(x0)*(x - x0)
在进行展开时,将估计值作为 x0 ,因为估计值是确定的值,实际状态 x 作为 x来展开
对泰勒展开式来说,f(x0) 相当于是常数项。
估计方程与量测方程
线性卡尔曼滤波的离散估计状态方程与量测方程为:
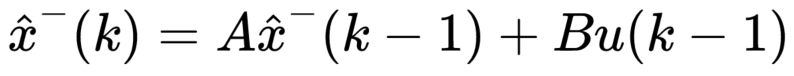

其中 z(k) 为量测值,H 为量测值与状态 x 之间的关系矩阵。
在 EKF 中,将等式右侧的项都看作是一个非线性函数,也就是状态方程中,将等式右边的关于x_hat 与 u 关系式都记作 f,量测方程中,等式右边的函数关系记作是 h 即:


其中,f 是非线性状态函数,h 是非线性量测函数,w 与 v 分别是高斯噪声,协方差矩阵为 Q 与 R,在上式中省略了。
在 EKF 的求解中,将 f 与 h 进行泰勒展开,f(x0)与h(x0) 当作是常数项,x0 代入 x_hat,然后只保留前两项(在 x_hat(k) 处进行展开),将一阶偏导数分别记作 F 与 H,后续的卡尔曼公式会用到 F 与 H,其实 F 与 H 都是雅可比矩阵:

将偏导部分记作 F:
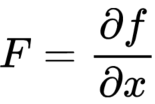
量测方程的非线性函数展开为:

将偏导部分记作 H:
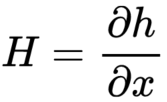
结合上面的非线性方程,之后将线性化的泰勒展开式代入上面的非线性方程。
状态估计方程
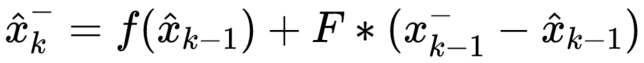
即,将非线性函数,在上次估计值 x_hat(k-1) 处进行泰勒展开,其中,f(x_hat(k-1)) 就是上一次的先验估计值,与 F*x_hat(k-1) 都是非随机值,将两个非随机值提出,得到:
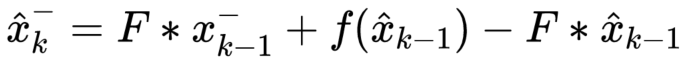
量测方程
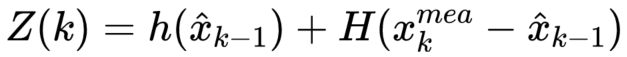
x_mea 为量测状态,同样的,将非随机值提出,得到:
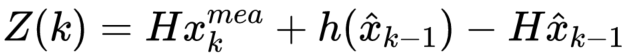
协方差矩阵与卡尔曼增益
根据先验估计的表达式,由 F 来代替,可以得出先验误差的协方差公式:
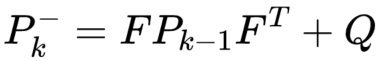
卡尔曼增益为:

后验估计与协方差矩阵更新
后验估计与协方差矩阵都与KF是相同的。
后验估计 = 先验估计值 + 卡尔曼增益*(量测值 - 先验估计输出):
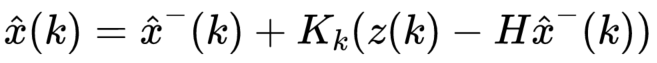
更新协方差:

EKF的更新公式
预测
先验估计值计算:
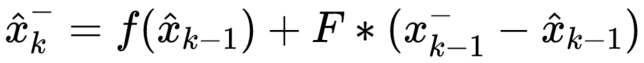
先验误差协方差计算:
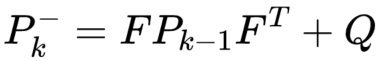
校正
卡尔曼增益计算:

后验估计值计算:
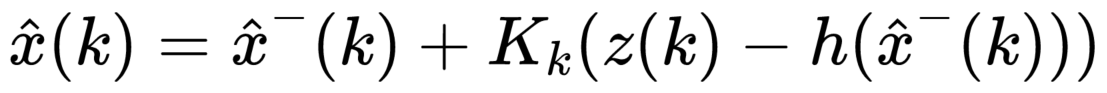

更新估计误差协方差:

一维非线性例子
这里直接采用了一本书上的比较典型的非线性例子,假设系统方程包含非线性项:
x(k) = 0.5*x(k-1) + 2.5*x(k-1) / (1 + x(k-1)^2) + 8*cos(1.2k) + w(k)
其中 w 为系统过程噪声。
观测方程为:
z(k) = x(k)^2 / 20 + v(k)
其中 v 为测量噪声
在上述例子中,系统方程与观测方程都包含非线性部分,在求解时,可以按照如下步骤:
1)状态预测,计算先验估计值
x(k)- = 0.5*x(k-1) + 2.5*x(k-1) / (1 + x(k-1)^2) + 8*cos(1.2k)
2)将上一步计算的先验估计值代入F与H更新线性化方程的偏导雅可比矩阵,分式求导法则: (u/v)' = (u'v-uv')/v²
F = 0.5 + (2.5 * (1+x^2) - 2.5*x*2*x) / (1+x^2)^2 = 0.5 + 2.5*(1-x^2) / (1+x^2)^2
H = x/10
3)求协方差矩阵的预测矩阵 Pk-
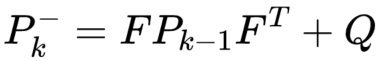
4)求卡尔曼滤波增益K

5)更新状态
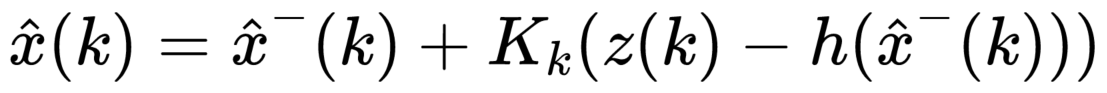
例如:xt 为上时刻的估计状态,x为当前的先验估计值,则:
h(x) = h(xt) + H*(x - xt)
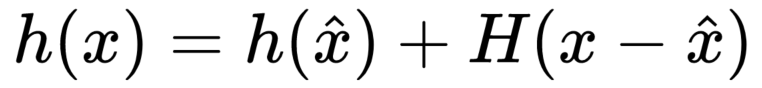
6)更新协方差 Pk

在实际测试中,将量测值加入一定范围的噪声,最后的效果如图:

相关文章:

【EKF】EKF原理
原理简述 卡尔曼滤波可以在线性模型,误差为高斯模型的情况下,对目标状态得出很好的估计效果,但如果系统存在非线性的因素,其效果就没有那么好了。比较典型的非线性函数关系包括平方关系,对数关系,指数关系…...
)
蓝桥杯官网填空题(古堡算式)
题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 福尔摩斯到某古堡探险,看到门上写着一个奇怪的算式:ABCDE ∗ ?EDCBA 他对华生说:“ABCDE 应该代表不同的数字,问号…...

Python---集合set
集合特点 1. 可以容纳多个数据 2. 可以容纳不同类型的数据 3.数据是无序存储的(不支持下标索引) 4. 不允许重复数据存在 5. 可以修改 6. 支持for循环,不支持while循环 集合定义 # 定义集合 变量 {元素1, 元素2, 元素3, 元素4...}# 定…...
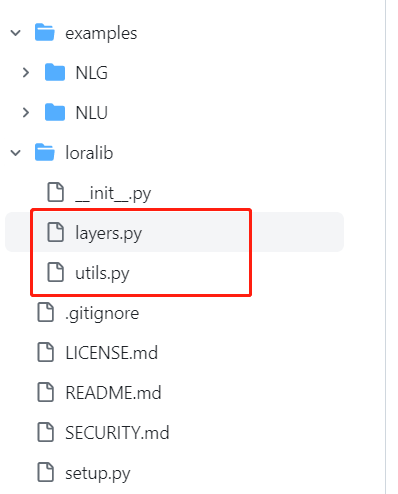
LORA项目源码解读
大模型fineturn技术中类似于核武器的LORA,简单而又高效。其理论基础为:在将通用大模型迁移到具体专业领域时,仅需要对其高维参数的低秩子空间进行更新。基于该朴素的逻辑,LORA降低大模型的fineturn门槛,模型训练时不需…...

Azure + React + ASP.NET Core 项目笔记一:项目环境搭建(一)
不重要的目录标题 前提条件第一步:新建文件夹第二步:使用VS/ VS code/cmd 打开该文件夹第三步:安装依赖第四步:试运行react第五步:整理项目结构 前提条件 安装dotnet core sdk 安装Node.js npm 第一步:新…...

html 学习 之 文本标签
下面是一些常见的HTML文本标签(,,,,和)以及它们的作用: 标签 (Emphasis - 强调): 作用:用于在文本中表示强调或重要性。 示例: <p>这是一段文本,&l…...

联发科3纳米芯片预计2024年量产,此前称仍未获批给华为供货
9月7日,联发科与台积电共同宣布,联发科首款采用台积电3纳米制程生产的天玑旗舰芯片开发进度顺利,已成功流片,预计将在2024年量产,并将于下半年正式上市。这款旗舰芯片并非今年上市的天玑9300。 据联发科总经理陈冠州介…...
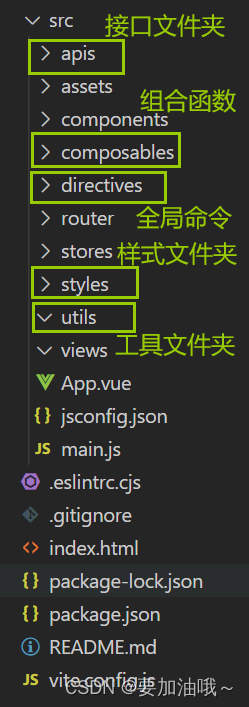
搭建vue3项目并git管理
搭建vue3项目 采用vue3的create-vue脚手架搭建项目,底层是vite,要求环境 node 16.0及以上(node -v检查node版本) 在文件夹右键->终端-> npm init vuelatest,输入项目名称,根据需要选择是否装包 src…...

【Azure OpenAI】OpenAI Function Calling 101
概述 本文是结合 github:OpenAI Function Calling 101在 Azure OpenAI 上的实现: Github Function Calling 101 如何将函数调用与 Azure OpenAI 服务配合使用 - Azure OpenAI Service 使用像ChatGPT这样的llm的困难之一是它们不产生结构化的数据输出…...
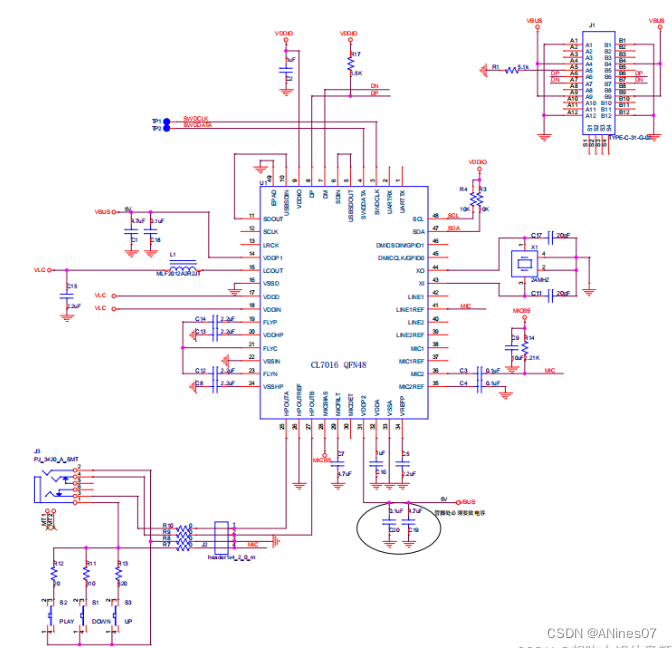
立晶半导体Cubic Lattice Inc 专攻音频ADC,音频DAC,音频CODEC,音频CLASS D等CL7016
概述: CL7016是一款高保真USB Type-C兼容音频编解码芯片。可以录制和回放有24比特音乐和声音。内置回放通路信号动态压缩, 最大42db录音通路增益,PDM数字麦克风,和立体声无需电容耳机驱动放大器。 5V单电源供电。兼容USB 2.0全速工…...
)
【Flutter】支持多平台 多端保存图片到本地相册 (兼容 Web端 移动端 android 保存到本地)
免责声明: 我只测试了Web端 和 Android端 可行哈 import dart:io; import package:flutter/services.dart; import package:http/http.dart as http; import package:universal_html/html.dart as html; import package:oktoast/oktoast.dart; import package:image_gallery_sa…...

postgresql 安装教程
postgresql 安装教程 本文以window 15版本为教程 文章目录 postgresql 安装教程1.下载地址2.以管理员身份运行3.选择安装路径,点击Next4.选择组件(默认都勾选),点击Next5.选择数据存储路径,点击Next6.设置超级用户的…...
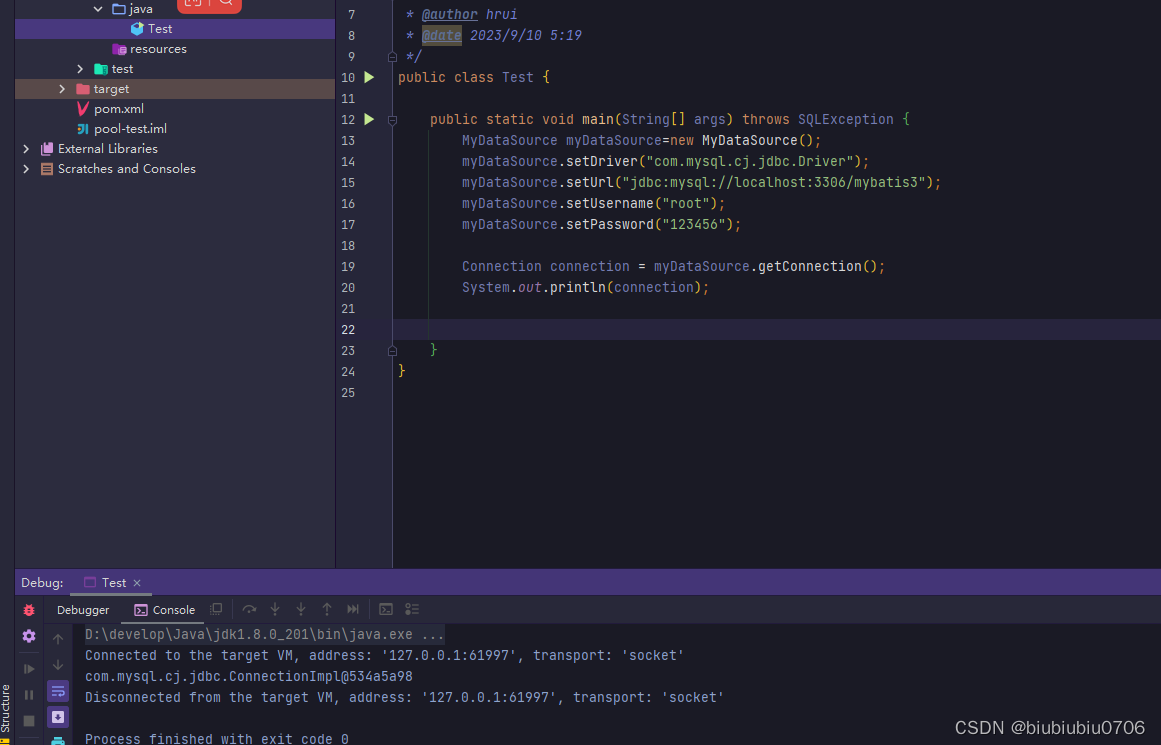
手写数据库连接池
数据库连接是个耗时操作.对数据库连接的高效管理影响应用程序的性能指标. 数据库连接池正是针对这个问题提出来的. 数据库连接池负责分配,管理和释放数据库连接.它允许应用程序重复使用一个现有的数据路连接,而不需要每次重新建立一个新的连接,利用数据库连接池将明显提升对数…...

在CentOS7上增加swap空间
在CentOS7上增加swap空间 在CentOS7上增加swap空间,可以按照以下步骤进行操作: 使用以下命令检查当前swap使用情况: swapon --show创建一个新的swap文件。你可以根据需要指定大小。例如,要创建一个2GB的swap文件,使用…...
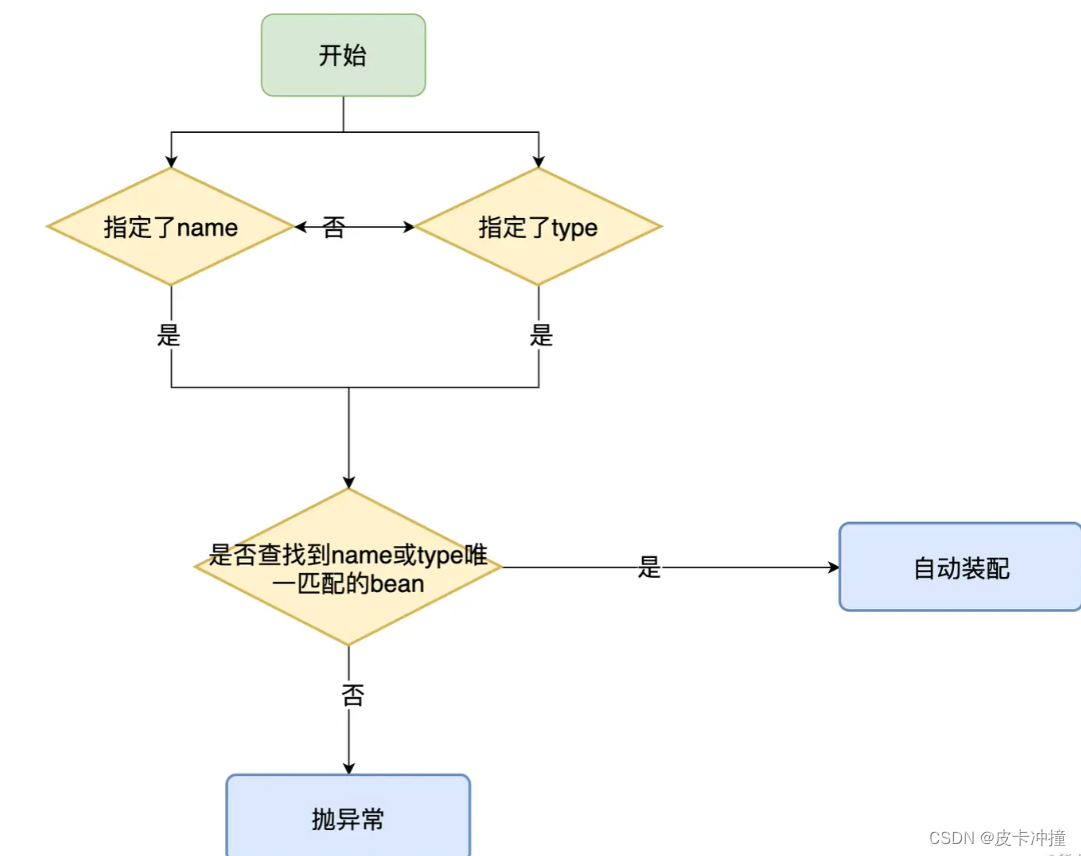
@Autowired和@Resource
文章目录 简介Autowired注解什么是Autowired注解Autowired注解的使用方式Autowired注解的优势和不足 Qualifier总结: Resource注解什么是Resource注解Resource注解的使用方式Resource注解的优势和不足 Autowired vs ResourceAutowired和Resource的区别为什么推荐使用…...
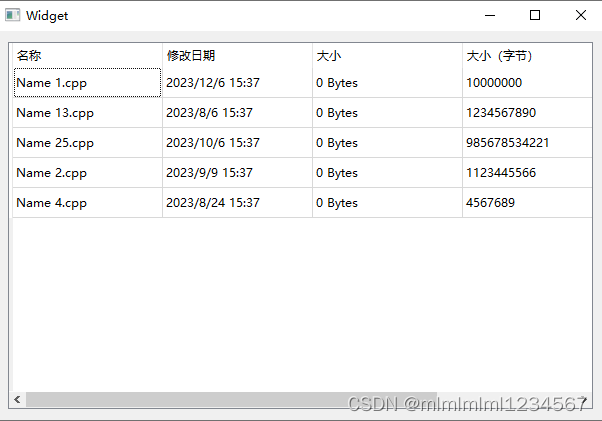
QTableView通过setColumnWidth设置了列宽无效的问题
在用到QT的QTableView时,为了显示效果,向手动的设置每一列的宽度,但是如下的代码是无效的。 ui->tableView->setColumnWidth(0,150);ui->tableView->setColumnWidth(1,150);ui->tableView->setColumnWidth(2,150);ui->t…...

【用unity实现100个游戏之10】复刻经典俄罗斯方块游戏
文章目录 前言开始项目网格生成Block方块脚本俄罗斯方块基类,绘制方块形状移动逻辑限制移动自由下落下落后设置对应风格为不可移动类型检查当前方块是否可以向指定方向移动旋转逻辑消除逻辑游戏结束逻辑怪物生成源码参考完结 前言 当今游戏产业中,经典游…...

Docker容器内数据备份到系统本地
Docker运行容器时没将目录映射出来,或者因docker容器内外数据不一致,导致docker运行错误的,可以使用以下步骤处理: 1.进入要备份的容器: docker exec -it <容器名称或ID> /bin/bash2.在容器内创建一个临时目录…...
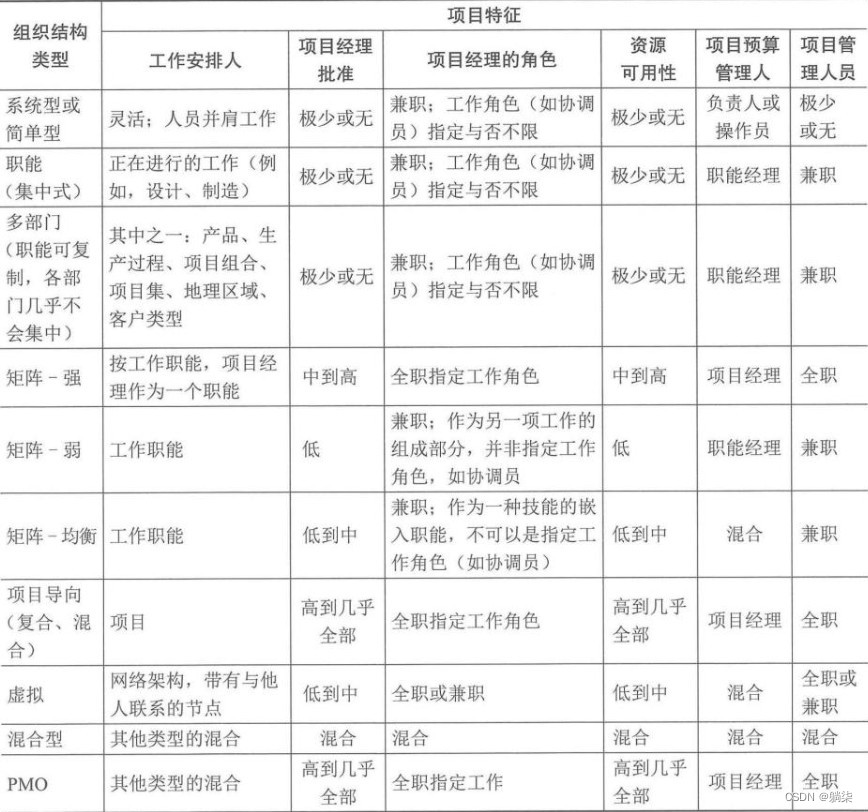
学信息系统项目管理师第4版系列06_项目管理概论
1. 项目基础 1.1. 项目是为创造独特的产品、服务或成果而进行的临时性工作 1.1.1. 独特的产品、服务或成果 1.1.2. 临时性工作 1.1.2.1. 项目有明确的起点和终点 1.1.2.2. 不一定意味着项目的持续时间短 1.1.2.3. 临时性是项目的特点,不是项目目标的特点 1.1…...
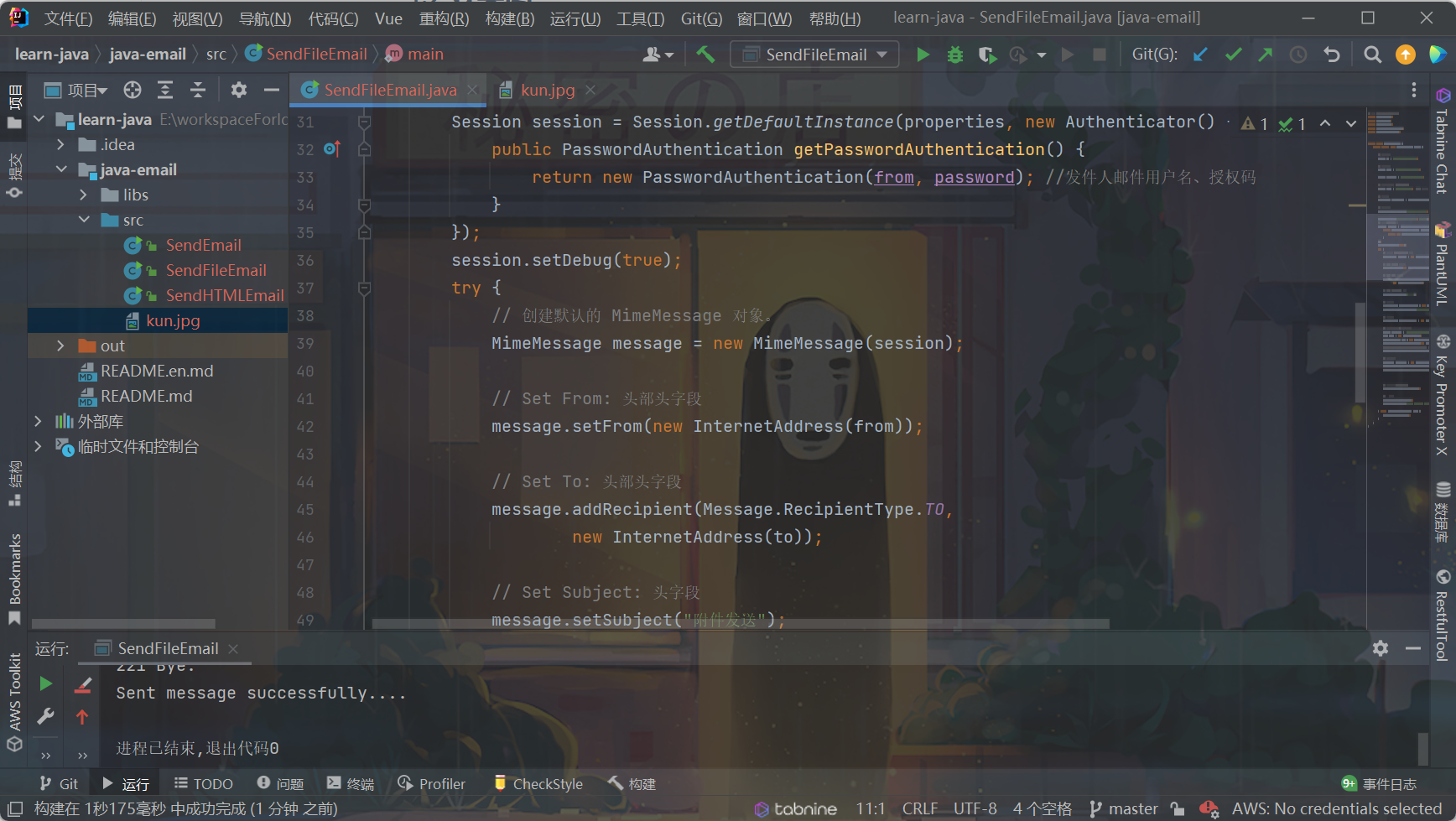
Java发送(QQ)邮箱、验证码发送
前言 使用Java应用程序发送 E-mail 十分简单,但是首先需要在项目中导入 JavaMail API 和Java Activation Framework (JAF) 的jar包。 菜鸟教程提供的下载链接: JavaMail mail.jar 1.4.5JAF(版本 1.1.1) activation.jar 1、准备…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...
