Leetcode.174 地下城游戏
题目链接
Leetcode.174 地下城游戏
hard
题目描述
恶魔们抓住了公主并将她关在了地下城 d u n g e o n dungeon dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 0 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0 0 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快解救公主,骑士决定每次只 向右 或 向下 移动一步。
返回确保骑士能够拯救到公主所需的最低初始健康点数。
注意:任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
示例 1:
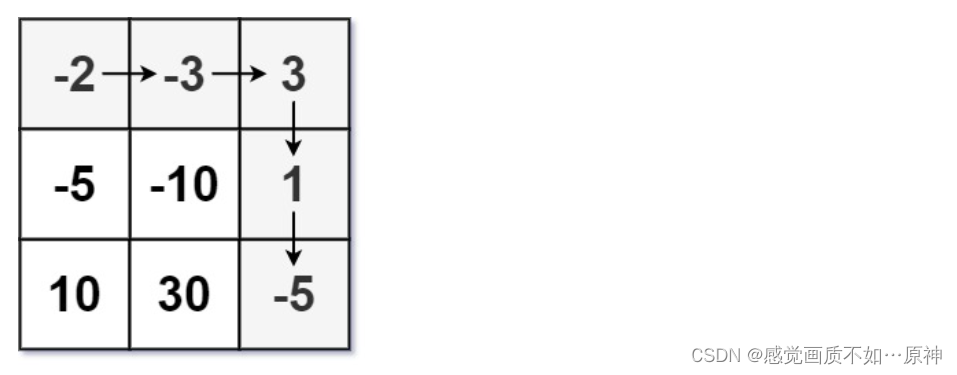
输入:dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
输出:7
解释:如果骑士遵循最佳路径:右 -> 右 -> 下 -> 下 ,则骑士的初始健康点数至少为 7 。
示例 2:
输入:dungeon = [[0]]
输出:1
提示:
- m = d u n g e o n . l e n g t h m = dungeon.length m=dungeon.length
- n = d u n g e o n [ i ] . l e n g t h n = dungeon[i].length n=dungeon[i].length
- 1 ≤ m , n ≤ 200 1 \leq m, n \leq 200 1≤m,n≤200
- − 1000 ≤ d u n g e o n [ i ] [ j ] ≤ 1000 -1000 \leq dungeon[i][j] \leq 1000 −1000≤dungeon[i][j]≤1000
解法:动态规划
假设我们考虑从左上角到右下角,这样的话我们需要考虑两个因素:当前路径和 ,当前路径上的最小路径和。因为存在两个同等重要的因素,所以我们无法确定下一个位置。
既然从左上角到右下角不行,那么我们就考虑从右下角到左上角。
考虑从右下角到左上角,我们定义 f ( i , j ) f(i,j) f(i,j) 为从位置 ( i , j ) (i,j) (i,j) 到终点 ( m − 1 , n − 1 ) (m-1,n-1) (m−1,n−1)所需要的最低初始健康点数。按照定义,最终我们返回的结果就是 f ( 0 , 0 ) f(0,0) f(0,0)。
f ( i , j ) f(i,j) f(i,j) 只与 f ( i + 1 , j ) f(i + 1,j) f(i+1,j) 和 f ( i , j + 1 ) f(i,j+1) f(i,j+1) 以及 d u n g e o n [ i ] [ j ] dungeon[i][j] dungeon[i][j] 有关。
即 f ( i , j ) = m i n { f [ i + 1 ] [ j ] , f [ i ] [ j + 1 ] } − d u n g e o n [ i ] [ j ] f(i,j) = min \{ f[i + 1][j] , f[i][j + 1] \} - dungeon[i][j] f(i,j)=min{f[i+1][j],f[i][j+1]}−dungeon[i][j]。
因为 f [ i ] [ j ] f[i][j] f[i][j] 必须是 ≥ 1 \geq1 ≥1 的,所以最终的转移方程为:
f ( i , j ) = m a x { m i n ( f [ i + 1 ] [ j ] , f [ i ] [ j + 1 ] ) − d u n g e o n [ i ] [ j ] , 1 } f(i,j) = max \{ min ( f[i + 1][j] , f[i][j + 1] ) - dungeon[i][j],1\} f(i,j)=max{min(f[i+1][j],f[i][j+1])−dungeon[i][j],1}
当 i = m − 1 i =m - 1 i=m−1 或者 j = n − 1 j = n- 1 j=n−1时, f [ i + 1 ] [ j ] f[i+1][j] f[i+1][j] 和 f [ i ] [ j + 1 ] f[i][j+1] f[i][j+1] 就会分别越界。初始直接定义 f [ i ] [ j ] f[i][j] f[i][j] 为一个较大的值,这里我设置的是 1 0 9 10^9 109。
特别需要注意的是,我们直接把 f [ m ] [ n − 1 ] f[m][n-1] f[m][n−1] 和 f [ m − 1 ] [ n ] f[m-1][n] f[m−1][n] 设置为 1 1 1,这样是为了让 f [ m − 1 ] [ n − 1 ] = d u n g e o n [ m − 1 ] [ n − 1 ] f[m-1][n-1] = dungeon[m-1][n-1] f[m−1][n−1]=dungeon[m−1][n−1]。
时间复杂度: O ( m × n ) O(m \times n) O(m×n)
C++代码:
class Solution {
public:int calculateMinimumHP(vector<vector<int>>& g) {int m = g.size() , n = g[0].size();vector<vector<int>> f(m + 1,vector<int>(n + 1,1e9));f[m][n - 1] = 1;f[m - 1][n] = 1;for(int i = m - 1;i >= 0;i--){for(int j = n - 1;j >= 0;j--){int t = min(f[i + 1][j],f[i][j + 1]);f[i][j] = max(t - g[i][j] , 1);}}return f[0][0];}
};
相关文章:

Leetcode.174 地下城游戏
题目链接 Leetcode.174 地下城游戏 hard 题目描述 恶魔们抓住了公主并将她关在了地下城 d u n g e o n dungeon dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公…...
python实现adb辅助点击屏幕工具
#!/usr/bin/env python # -*- coding: utf-8 -*-import re import os import time import subprocess import tkinter as tk from tkinter import messagebox from PIL import Image, ImageTk# 设置ADB路径(根据你的系统和安装路径进行调整) ADB_PATH C…...
智能合约安全分析,针对 ERC777 任意调用合约 Hook 攻击
智能合约安全分析,针对 ERC777 任意调用合约 Hook 攻击 Safful发现了一个有趣的错误,有可能成为一些 DeFi 项目的攻击媒介。这个错误尤其与著名的 ERC777 代币标准有关。此外,它不仅仅是众所周知的黑客中常见的简单的重入问题。 这篇文章对 …...

nodejs 爬虫 axios 异步爬虫 教程 【一】
axios 自定义headers axios.defaults.headers.common["User-Agent"] "Googlebot/2.1 (http://www.google.com/bot.html)"; 运行环境: node :v18 const axios require("axios"); axios.defaults.headers.common["U…...
)
Swift学习笔记三(Dictionary 篇)
1 Dictionary 概念 字典储存无序的互相关联的同一类型的键和同一类型的值的集合。字典类型的全写方式 Dictionary<Key, Value>,简写方式 [Key: Value],建议使用简写方式。字典的 key 必须是可哈希的。 2 Dictionary创建 2.1 初始器创建方式 2.2 …...

javax.mail 遇到501 mail from address must be same as authorization user 的問題
使用不同的兩個帳戶发送email时,第一个账户可以发送成功,但到第二个账户的时候就报出了501 mail from address must be same as authorization user的错误。 具体代码如下: import java.util.Date; import java.util.List; import java.util.…...
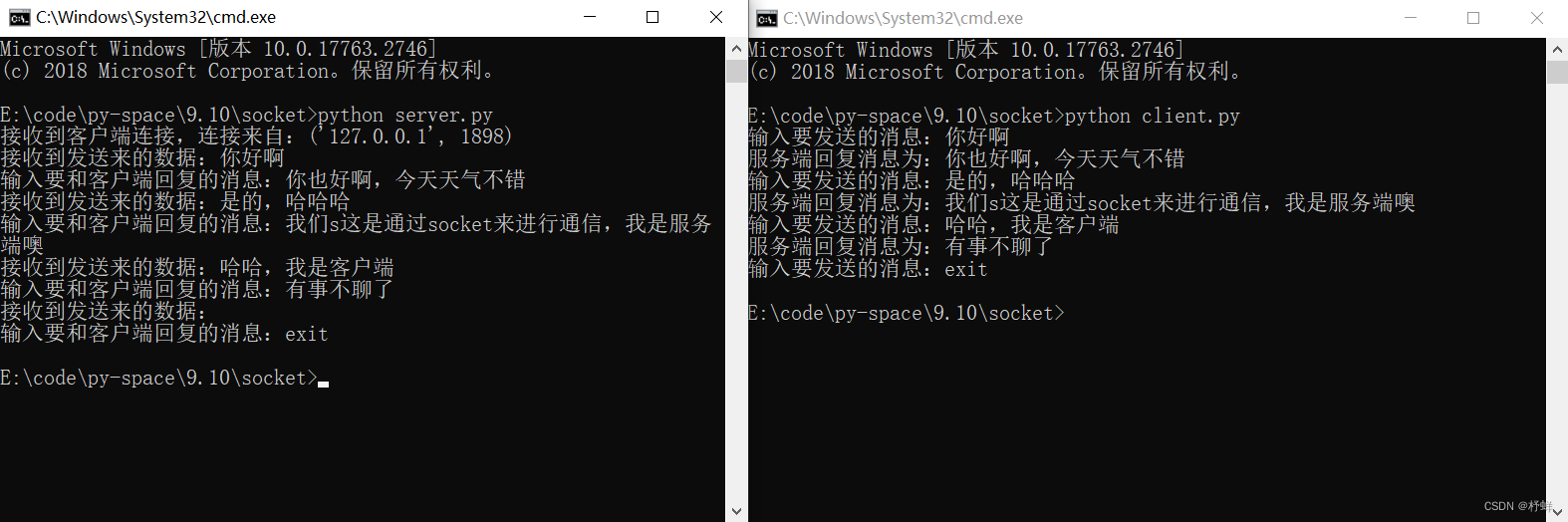
【Python】网络编程
Socket Socket (简称 套接字)是进程之间通信一个工具,进程之间想要进行网络通信需要socket。Socket负责进程之间的网络数据传输,好比数据的搬运工。 客户端和服务端 2个进程之间通过Socket进行相互通讯,就必须有服务端和客户端 Socket服务…...

客户端开发常用框架
在Unity游戏开发中,客户端常用的框架包括以下几种: 1.Unity的网络框架:Unity自带了网络框架,包括Unity Networking、Unity Matchmaker和Unity Remote等。这些框架可以帮助我们进行游戏的联机对战、排行榜、跨平台等功能的设计和实…...

数据分析综述
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...

区块链技术与应用 - 学习笔记2【密码学基础】
大家好,我是比特桃。本系列笔记只专注于探讨研究区块链技术原理,不做其他违反相关规定的讨论。 区块链技术已被纳入国家十四五规划,在“加快数字发展 建设数字中国”篇章中,区块链被列为“十四五”七大数字经济重点产业之一&#…...

制作Linux发行版安装镜像:复刻centos镜像安装ISO
制作Linux发行版安装镜像:复刻centos镜像安装ISO 我们平时经常下载Linux各个发行版,下载ISO,安装使用。那么ISO到底是如何制作的?安装过程是什么原理? 近来打算讲镜像制作的过程、原理,通过一个专栏分享一…...

【复习socket】每天40min,我们一起用70天稳扎稳打学完《JavaEE初阶》——29/70 第二十九天
专注 效率 记忆 预习 笔记 复习 做题 欢迎观看我的博客,如有问题交流,欢迎评论区留言,一定尽快回复!(大家可以去看我的专栏,是所有文章的目录) 文章字体风格: 红色文字表示:重难点★✔ 蓝色文字表示:思路以及想法★✔ 如果大家觉得有帮助的话,感谢大家帮忙 点…...

postgresql-常用数学函数
postgresql-常用数学函数 案例 案例 --求余 1 select 5%2 as t; --绝对值 17.4 select abs(-17.4) as t2; -- 大于等于最小整数 -42 select ceil(-42.8) as t3; -- 小于等于的最大整数 42 select floor(42.3) as t4; -- 四舍五入 44 select round(43.6) as t5; -- 向零取整 12…...
:常用命令与最佳实践)
Docker实战技巧(一):常用命令与最佳实践
一、原理 1、Hypervisor是一种运行在物理服务器和操作系统之间的中间软件层,可允许多个操作系统和应用共享一套基础物理硬件,它能直接访问物理设备,会给每一台虚拟机分配内存、CPU、网络、磁盘等资源,也可以确保虚拟机对应的硬…...
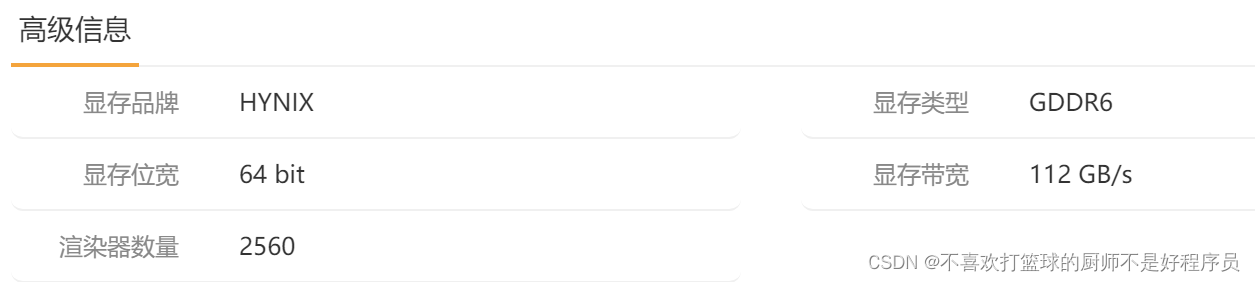
使用CUDA计算GPU的理论显存带宽
文章目录 一、显存带宽和理论显存带宽1. 显存带宽2. 理论显存带宽1)计算公式2)举例 二、利用CUDA计算理论显存带宽 一、显存带宽和理论显存带宽 1. 显存带宽 显存带宽是指显存和GPU计算单元之间的数据传输速率。 显存带宽越大,意味着数据传…...
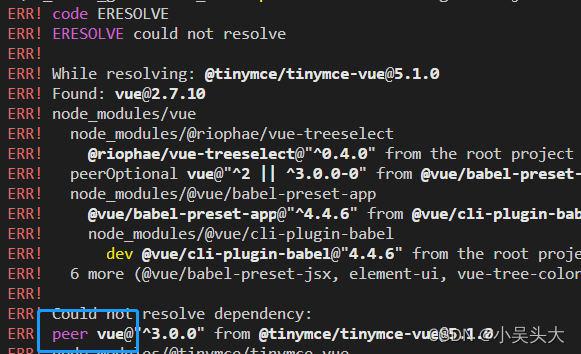
npm install依赖冲突解决办法
今天npm的时候发现报错,原来是依赖冲突了 npm后面加上这个指令就可以顺利的安装依赖了。问题主因就是不同开发用了不同版本node导致依赖版本不同,出现了成功冲突,这是段指令;它告诉npm忽略项目中引入的各个依赖模块之间依赖相同但…...

植物大战僵尸各种僵尸攻略
前言 此文章为“植物大战僵尸”专栏中的009刊(2023年9月第八刊),欢迎订阅。版权所有。 注意: 1.本博客适用于pvz无名版; 2.pvz指植物大战僵尸(Plants VS Zonbies); 3.本文以耗费低做标准&am…...

Scrum敏捷开发企业实战培训
课程简介 Scrum是目前运用最为广泛的敏捷开发方法,是一个轻量级的项目管理和产品研发管理框架。 这是一个两天的实训课程,面向研发管理者、项目经理、产品经理、研发团队等,旨在帮助学员全面系统地学习Scrum和敏捷开发, 帮助企业快速启动敏…...
uniapp 下拉框数据回显的问题
问题 : 现在是下拉框数据回显不了, 绑定的v-model 原因 : uniui 下拉框数据绑定要是 value text 这种格式的 解决办法: 将获取到的后端数据 转换为 需要的格式 ,再进行绑定 下拉框的数据 遍历...

使用php 获取时间今天、明天、昨天时间戳的详解
使用php获取时间今、明天、昨天时间戳 <?php echo "今天:".date("Y-m-d").""; echo "昨天:".date("Y-m-d",strtotime("-1 day")), ""; echo "明天:".date("Y-m-d&qu…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
