D. Paths on the Tree
Problem - 1746D - Codeforces
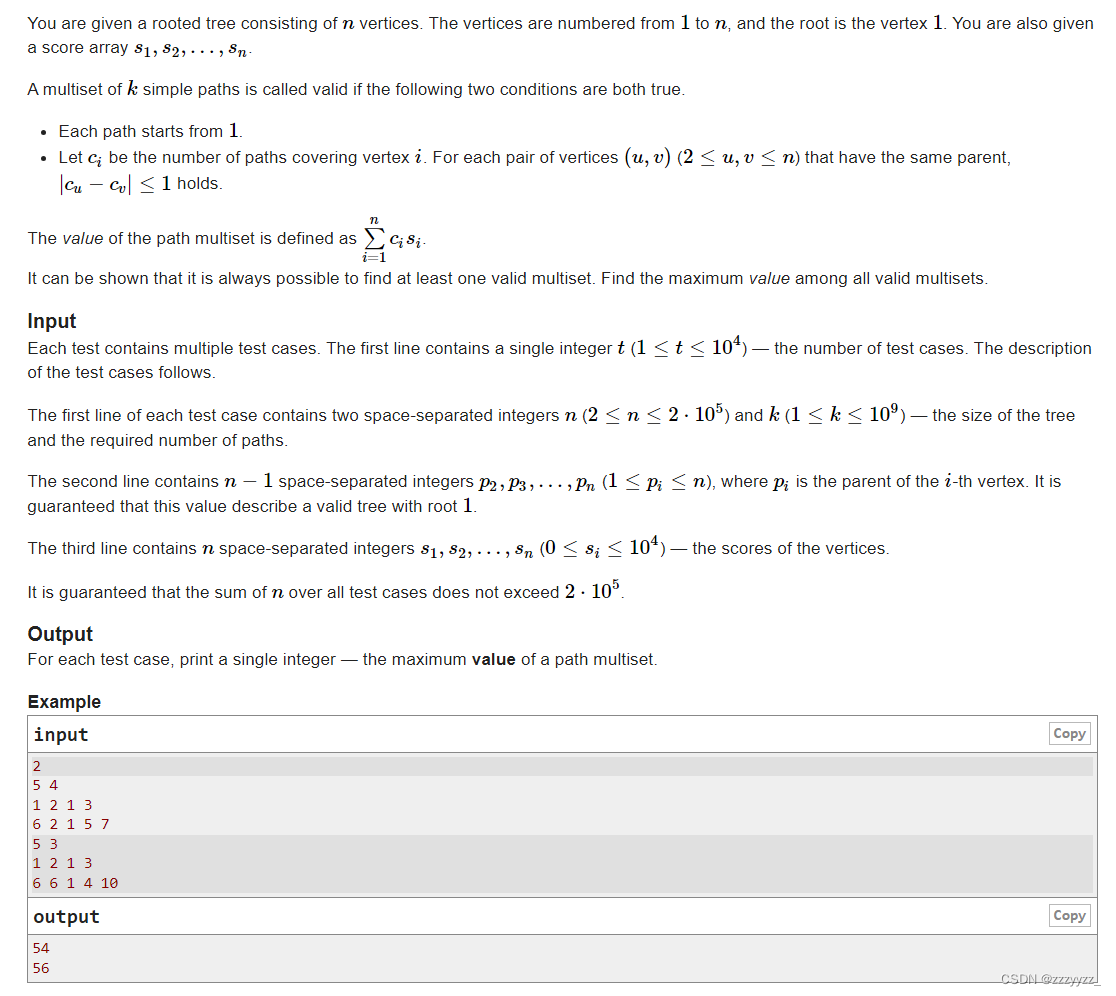
思路:先分析一下题意,根据第一条性质,每次只能够从1开始,而第二条性质则表明对于每个节点来说,经过这个节点的子节点的路径条数应该尽量均衡,最大值与最小值相差不能超过1,所以我们考虑,如果当前要选择k个路径,而当前节点有cnt个子节点,那么每个子节点应该至少经过k/cnt个,同时有k%cnt个需要经过k/cnt+1个,那么我们发现这个问题可以递归的解决,那么我们可以考虑用树形dp,我们将f[i][0]表示以i为根,并且经过ki个,f[i][1]表示以i为根并且经过ki+1个,那么对于叶子节点来说,f[i][0]=cost[i]*k,f[i][1]=cost[i]*(k+1),而对于非叶子节点来说,因为所有的子节点都至少经过ki个,所有我们先将所有子节点的f[j][0]求和为sum,令f[i][0]=f[i][1]=sum,那么我们还要再经过k%cnt个,那么我们就是挑几个子节点,然后让他变为f[j][1],那么我们可以将所有f[j][1]-f[j][0]排个序,按照降序排序,那么我们只需要将差值加上,就相当于这个变为了f[j][1],所以我们只需要求一下前k%cnt的和即可,这是对于f[i][0]来说,而对于f[i][1]来说,则还要多出来一次,那么我们只需要求和倒k%cnt+1即可,并且k%cnt+1按照相同的方法取最大的k%cnt+1个一定也是正确的,因为k%cnt最大为cnt-1个,加一为cnt个,正好等于子节点的个数,所以一定是合法的取法
// Problem: D. Paths on the Tree
// Contest: Codeforces - Codeforces Global Round 23
// URL: https://codeforces.com/problemset/problem/1746/D
// Memory Limit: 256 MB
// Time Limit: 3000 m#include<bits/stdc++.h>
#include<sstream>
#include<cassert>
#define fi first
#define se second
#define i128 __int128
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int,int> PII;
const double eps=1e-7;
const int N=5e5+7 ,M=5e5+7, INF=0x3f3f3f3f,mod=1e9+7,mod1=998244353;
const long long int llINF=0x3f3f3f3f3f3f3f3f;
inline ll read() {ll x=0,f=1;char c=getchar();while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') {x=(ll)x*10+c-'0';c=getchar();} return x*f;}
inline void write(ll x) {if(x < 0) {putchar('-'); x = -x;}if(x >= 10) write(x / 10);putchar(x % 10 + '0');}
inline void write(ll x,char ch) {write(x);putchar(ch);}
void stin() {freopen("in_put.txt","r",stdin);freopen("my_out_put.txt","w",stdout);}
bool cmp0(int a,int b) {return a>b;}
template<typename T> T gcd(T a,T b) {return b==0?a:gcd(b,a%b);}
template<typename T> T lcm(T a,T b) {return a*b/gcd(a,b);}
void hack() {printf("\n----------------------------------\n");}int T,hackT;
int n,m,k;
int h[N],e[M],ne[M],idx;
ll f[N][2];
int cost[N];void add(int a,int b) {e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}void dfs(int u,int k) {f[u][0]=(ll)cost[u]*k;f[u][1]=(ll)cost[u]*(k+1);int cnt=0;for(int i=h[u];i!=-1;i=ne[i]) {int j=e[i];cnt++;}if(!cnt) return ;int a=k/cnt,b=k%cnt;vector<ll> vis;for(int i=h[u];i!=-1;i=ne[i]) {int j=e[i];dfs(j,a);f[u][0]+=f[j][0];f[u][1]+=f[j][0];vis.push_back(f[j][1]-f[j][0]);}sort(vis.begin(),vis.end(),[&](ll &a,ll &b){return a>b;});for(int i=0;i<b;i++) f[u][0]+=vis[i];for(int i=0;i<=b;i++) f[u][1]+=vis[i];
}void solve() {n=read(),k=read();memset(h,-1,sizeof(int)*(n+4));idx=0;for(int i=2;i<=n;i++) {int c=read();add(c,i);}for(int i=1;i<=n;i++) cost[i]=read();dfs(1,k);printf("%lld\n",f[1][0]);
} int main() {// init();// stin();// ios::sync_with_stdio(false); scanf("%d",&T);// T=1; while(T--) hackT++,solve();return 0;
}
相关文章:

D. Paths on the Tree
Problem - 1746D - Codeforces 思路:先分析一下题意,根据第一条性质,每次只能够从1开始,而第二条性质则表明对于每个节点来说,经过这个节点的子节点的路径条数应该尽量均衡,最大值与最小值相差不能超过1&am…...

CocosCreator3.8研究笔记(九)CocosCreator 场景资源的理解
相信很多朋友都想知道, Cocos Creator 资源的定义? Cocos Creator 常见的资源包含哪些?Cocos Creator 资源的管理机制是什么样的? Cocos Creator 中所有继承自 Asset 的类型都统称资源 ,例如:Texture2D、Sp…...
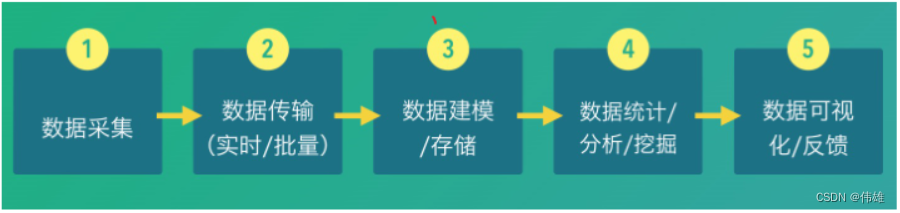
大数据课程L1——网站流量项目的概述整体架构
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解网站流量项目的案例概述; ⚪ 了解网站流量项目的数据埋点和采集; ⚪ 了解网站流量项目的整体架构; 一、网站流量项目概述 1. 背景说明 网站流量统计是改进网站服务的重要手段之一…...
提升数据库安全小技巧,使用SSH配合开源DBeaver工具连接数据库
title: 提升数据库安全小技巧,使用SSH配合开源DBeaver工具连接数据库 categories: 独立博客的方方面面 前段时间, 未来降低网址运行成本,搭了一套Mysql Docker 数据库, 包括外部链接,数据备份,数据导出,数据恢复一套解…...

信息安全技术概论-李剑-持续更新
图片和细节来源于 用户 xiejava1018 一.概述 随着计算机网络技术的发展,与时代的变化,计算机病毒也经历了从早期的破坏为主到勒索钱财敲诈经济为主,破坏方式也多种多样,由早期的破坏网络到破坏硬件设备等等 ,这也…...
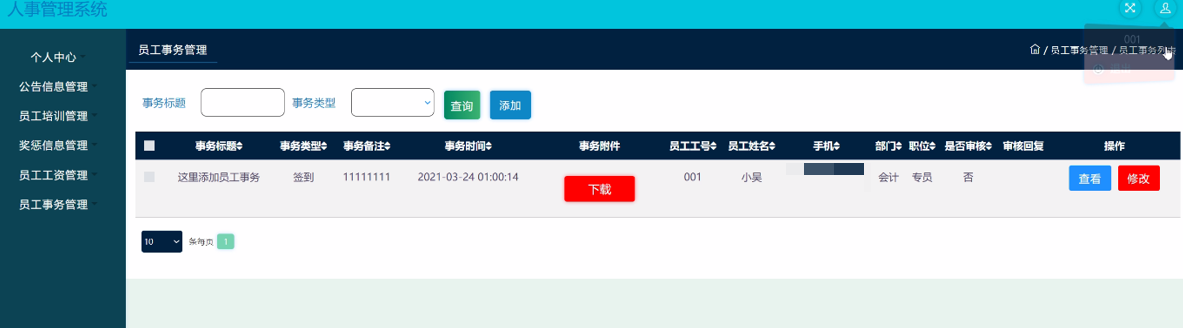
java项目基于 SSM+JSP 的人事管理系统
java项目基于 SSMJSP 的人事管理系统 博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W,Csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 大家好,今天和大家聊的是 Java 基于 SSM 的人事管理系统。…...
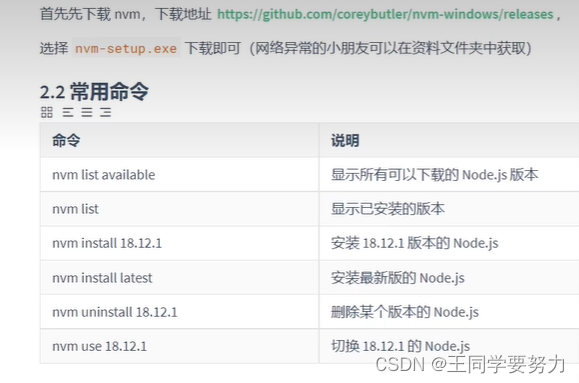
【Node.js】—基本知识点总结
【Node.js】—基本知识总结 一、命令行常用操作 二、Node.js注意点 Node.js中不能使用BOM和DOM操作 总结 三、Buffer buffer是一个类似于数组的对象,用于表示固定长度的字节序列buffer的本质是一段内存空间,专门用来处理二进制数据 特点:…...
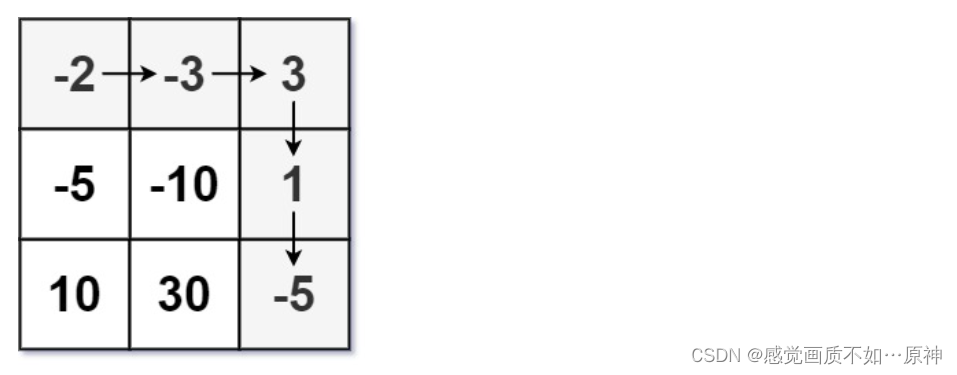
Leetcode.174 地下城游戏
题目链接 Leetcode.174 地下城游戏 hard 题目描述 恶魔们抓住了公主并将她关在了地下城 d u n g e o n dungeon dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公…...
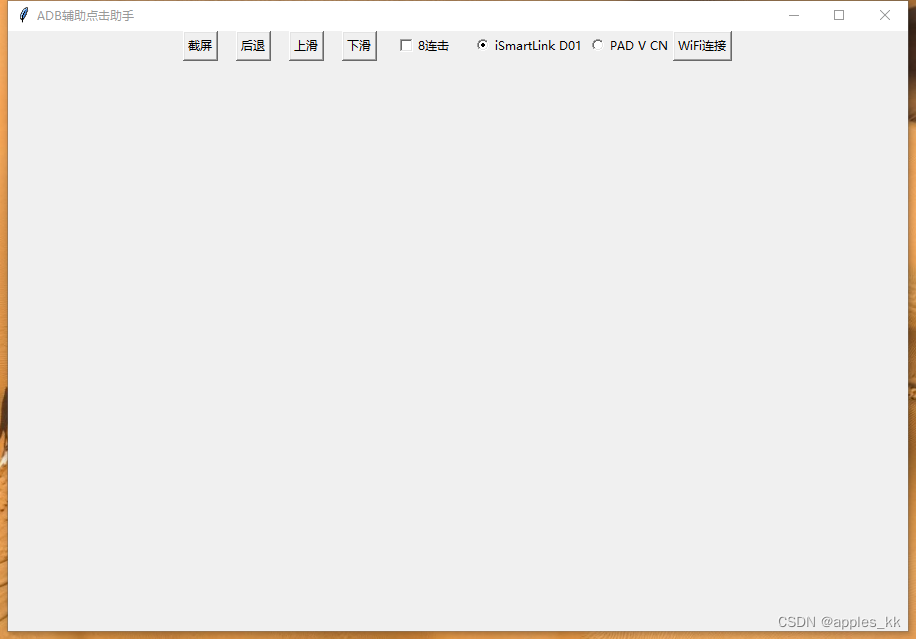
python实现adb辅助点击屏幕工具
#!/usr/bin/env python # -*- coding: utf-8 -*-import re import os import time import subprocess import tkinter as tk from tkinter import messagebox from PIL import Image, ImageTk# 设置ADB路径(根据你的系统和安装路径进行调整) ADB_PATH C…...
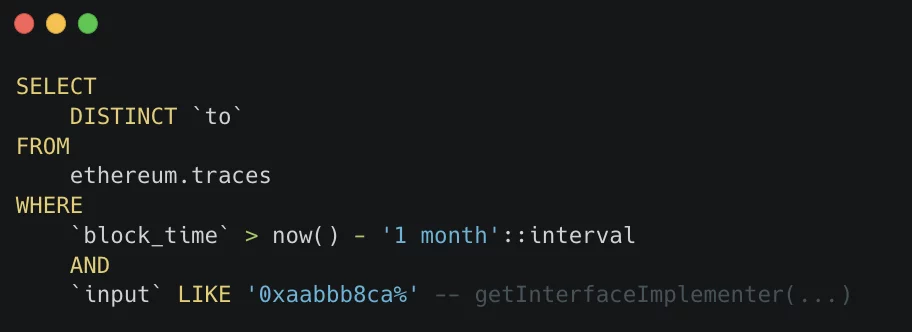
智能合约安全分析,针对 ERC777 任意调用合约 Hook 攻击
智能合约安全分析,针对 ERC777 任意调用合约 Hook 攻击 Safful发现了一个有趣的错误,有可能成为一些 DeFi 项目的攻击媒介。这个错误尤其与著名的 ERC777 代币标准有关。此外,它不仅仅是众所周知的黑客中常见的简单的重入问题。 这篇文章对 …...

nodejs 爬虫 axios 异步爬虫 教程 【一】
axios 自定义headers axios.defaults.headers.common["User-Agent"] "Googlebot/2.1 (http://www.google.com/bot.html)"; 运行环境: node :v18 const axios require("axios"); axios.defaults.headers.common["U…...
)
Swift学习笔记三(Dictionary 篇)
1 Dictionary 概念 字典储存无序的互相关联的同一类型的键和同一类型的值的集合。字典类型的全写方式 Dictionary<Key, Value>,简写方式 [Key: Value],建议使用简写方式。字典的 key 必须是可哈希的。 2 Dictionary创建 2.1 初始器创建方式 2.2 …...

javax.mail 遇到501 mail from address must be same as authorization user 的問題
使用不同的兩個帳戶发送email时,第一个账户可以发送成功,但到第二个账户的时候就报出了501 mail from address must be same as authorization user的错误。 具体代码如下: import java.util.Date; import java.util.List; import java.util.…...
【Python】网络编程
Socket Socket (简称 套接字)是进程之间通信一个工具,进程之间想要进行网络通信需要socket。Socket负责进程之间的网络数据传输,好比数据的搬运工。 客户端和服务端 2个进程之间通过Socket进行相互通讯,就必须有服务端和客户端 Socket服务…...

客户端开发常用框架
在Unity游戏开发中,客户端常用的框架包括以下几种: 1.Unity的网络框架:Unity自带了网络框架,包括Unity Networking、Unity Matchmaker和Unity Remote等。这些框架可以帮助我们进行游戏的联机对战、排行榜、跨平台等功能的设计和实…...

数据分析综述
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...

区块链技术与应用 - 学习笔记2【密码学基础】
大家好,我是比特桃。本系列笔记只专注于探讨研究区块链技术原理,不做其他违反相关规定的讨论。 区块链技术已被纳入国家十四五规划,在“加快数字发展 建设数字中国”篇章中,区块链被列为“十四五”七大数字经济重点产业之一&#…...

制作Linux发行版安装镜像:复刻centos镜像安装ISO
制作Linux发行版安装镜像:复刻centos镜像安装ISO 我们平时经常下载Linux各个发行版,下载ISO,安装使用。那么ISO到底是如何制作的?安装过程是什么原理? 近来打算讲镜像制作的过程、原理,通过一个专栏分享一…...

【复习socket】每天40min,我们一起用70天稳扎稳打学完《JavaEE初阶》——29/70 第二十九天
专注 效率 记忆 预习 笔记 复习 做题 欢迎观看我的博客,如有问题交流,欢迎评论区留言,一定尽快回复!(大家可以去看我的专栏,是所有文章的目录) 文章字体风格: 红色文字表示:重难点★✔ 蓝色文字表示:思路以及想法★✔ 如果大家觉得有帮助的话,感谢大家帮忙 点…...

postgresql-常用数学函数
postgresql-常用数学函数 案例 案例 --求余 1 select 5%2 as t; --绝对值 17.4 select abs(-17.4) as t2; -- 大于等于最小整数 -42 select ceil(-42.8) as t3; -- 小于等于的最大整数 42 select floor(42.3) as t4; -- 四舍五入 44 select round(43.6) as t5; -- 向零取整 12…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...
