06-JVM对象内存回收机制深度剖析
上一篇:05-JVM内存分配机制深度剖析
堆中几乎放着所有的对象实例,对堆垃圾回收前的第一步就是要判断哪些对象已经死亡(即不能再被任何途径使用的对象)。
1.引用计数法
给对象中添加一个引用计数器,每当有一个地方引用它,计数器就加1;当引用失效,计数器就减1;任何时候计数器为0的对象就是不可能再被使用的。
这个方法实现简单,效率高,但是目前主流的虚拟机中并没有选择这个算法来管理内存,其最主要的原因是它很难解决对象之间相互循环引用的问题。 所谓对象之间的相互引用问题,如下面代码所示:除了对象objA 和 objB 相互引用着对方之外,这两个对象之间再无任何引用。但是他们因为互相引用对方,导致它们的引用计数器都不为0,于是引用计数算法无法通知 GC 回收器回收他们。
public class ReferenceCountingGc {Object instance = null;public static void main(String[] args) {ReferenceCountingGc objA = new ReferenceCountingGc();ReferenceCountingGc objB = new ReferenceCountingGc();objA.instance = objB;objB.instance = objA;objA = null;objB = null;}
}
2.可达性分析算法
将“GC Roots” 对象作为起点,从这些节点开始向下搜索引用的对象,找到的对象都标记为非垃圾对象,其余未标记的对象都是垃圾对象
GC Roots根节点:线程栈的本地变量、静态变量、本地方法栈的变量等等

3.常见引用类型
java的引用类型一般分为四种:强引用、软引用、弱引用、虚引用
**强引用:**普通的变量引用
public static User user = new User();
**软引用:**将对象用SoftReference软引用类型的对象包裹,正常情况不会被回收,但是GC做完后发现释放不出空间存放新的对象,则会把这些软引用的对象回收掉。软引用可用来实现内存敏感的高速缓存。
public static SoftReference<User> user = new SoftReference<User>(new User());
软引用在实际中有重要的应用,例如浏览器的后退按钮。按后退时,这个后退时显示的网页内容是重新进行请求还是从缓存中取出呢?这就要看具体的实现策略了。
- 如果一个网页在浏览结束时就进行内容的回收,则按后退查看前面浏览过的页面时,需要重新构建
- 如果将浏览过的网页存储到内存中会造成内存的大量浪费,甚至会造成内存溢出
弱引用: 将对象用WeakReference软引用类型的对象包裹,弱引用跟没引用差不多,GC会直接回收掉,很少用
public static WeakReference<User> user = new WeakReference<User>(new User());
虚引用: 虚引用也称为幽灵引用或者幻影引用,它是最弱的一种引用关系,几乎不用
4.finalize()方法最终判定对象是否存活
即使在可达性分析算法中不可达的对象,也并非是“非死不可”的,这时候它们暂时处于“缓刑”阶段,要真正宣告一个对象死亡,至少要经历再次标记过程。
标记的前提是对象在进行可达性分析后发现没有与GC Roots相连接的引用链。
- 第一次标记并进行一次筛选。
筛选的条件是此对象是否有必要执行finalize()方法。
当对象没有覆盖finalize方法,对象将直接被回收。 - 第二次标记
如果这个对象覆盖了finalize方法,finalize方法是对象脱逃死亡命运的最后一次机会,如果对象要在finalize()中成功拯救自己,只要重新与引用链上的任何的一个对象建立关联即可,譬如把自己赋值给某个类变量或对象的成员变量,那在第二次标记时它将移除出“即将回收”的集合。如果对象这时候还没逃脱,那基本上它就真的被回收了。
注意:一个对象的finalize()方法只会被执行一次,也就是说通过调用finalize方法自我救命的机会就一次。
示例代码:
public class OOMTest {public static void main(String[] args) {List<Object> list = new ArrayList<>();int i = 0;int j = 0;while (true) {list.add(new User(i++, UUID.randomUUID().toString()));new User(j--, UUID.randomUUID().toString());}}
}//User类需要重写finalize方法
@Override
protected void finalize() throws Throwable {OOMTest.list.add(this);System.out.println("关闭资源,userid=" + id + "即将被回收");
}
finalize()方法的运行代价高昂, 不确定性大, 无法保证各个对象的调用顺序, 如今已被官方明确声明为不推荐使用的语法。 有些资料描述它适合做“关闭外部资源”之类的清理性工作, 这完全是对finalize()方法用途的一种自我安慰。 finalize()能做的所有工作, 使用try-finally或者其他方式都可以做得更好、更及时, 所以建议大家完全可以忘掉Java语言里面的这个方法。
5.如何判断一个类是无用的类
方法区主要回收的是无用的类,那么如何判断一个类是无用的类呢?
类需要同时满足下面3个条件才能算是 “无用的类” :
- 该类所有的对象实例都已经被回收,也就是 Java 堆中不存在该类的任何实例。
- 加载该类的 ClassLoader 已经被回收。
- 该类对应的 java.lang.Class 对象没有在任何地方被引用,无法在任何地方通过反射访问该类的方法。
相关文章:

06-JVM对象内存回收机制深度剖析
上一篇:05-JVM内存分配机制深度剖析 堆中几乎放着所有的对象实例,对堆垃圾回收前的第一步就是要判断哪些对象已经死亡(即不能再被任何途径使用的对象)。 1.引用计数法 给对象中添加一个引用计数器,每当有一个地方引…...

[VSCode] 替换掉/去掉空行
VSCode中使用快捷键CtrlH,出现替换功能,在上面的“查找”框中输入正则表达式: ^\s*(?\r?$)\n然后选择右侧的“使用正则表达式”;“替换”框内为空,点击右侧的“全部替换”,即可去除所有空行。 参考 [VS…...
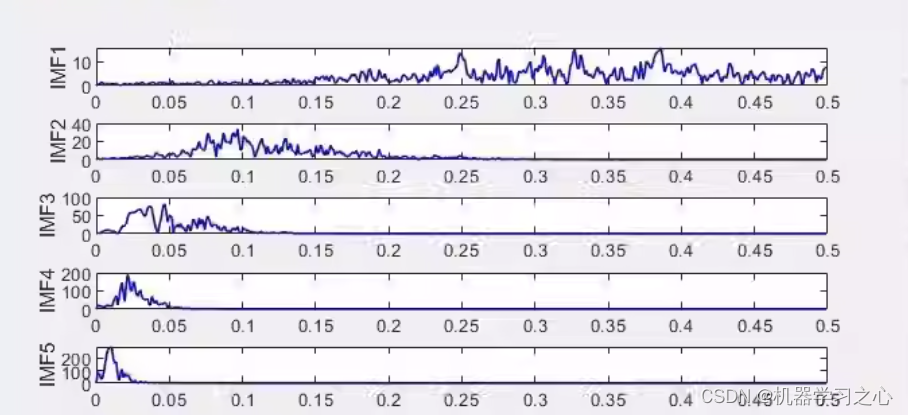
时序分解 | MATLAB实现ICEEMDAN+SE改进的自适应经验模态分解+样本熵重构分量
时序分解 | MATLAB实现ICEEMDANSE改进的自适应经验模态分解样本熵重构分量 目录 时序分解 | MATLAB实现ICEEMDANSE改进的自适应经验模态分解样本熵重构分量效果一览基本介绍程序设计参考资料 效果一览 基本介绍 ICEEMDANSE改进的自适应经验模态分解样本熵重构分量 包括频谱图 避…...

python内网环境安装第三方包【内网搭建开发环境】
文章目录 一、问题二、解决方法三、代码实现一、问题 内网安装第三方包的应用场景,一般是一些需要在没网的环境下进行开发的情况。这些环境一般仅支持本地局域网访问,所以只能在不下载任何第三方包的情况下艰难开发。 二、解决方法 将当前应用依赖的第三方包提前下载到本地…...

7.13 在SpringBoot中 正确使用Validation实现参数效验
文章目录 前言引入Maven依赖一、POST/PUT RequestBody参数校验1.1 Valid或Validated注解配合constraints注解1.2 测试运行 二、GET/DELETE RequestParam参数校验2.1 Validated注解配合constraints注解2.2 测试运行 三、GET 无注解参数校验3.1 Valid或Validated注解配合constrai…...

Matlab图像处理之Lee滤波器
目录 一、前言:二、LEE滤波器2.1 LEE滤波器原理2.2 LEE滤波器实现步骤三、MATLAB代码示例一、前言: LEE滤波器是一种常用于合成孔径雷达(SAR)图像去噪的滤波器。它能增强图像的局部对比度。今天我们将通过MATLAB来实现这种滤波器。 二、LEE滤波器 2.1 LEE滤波器原理 LEE滤…...

C++系列-const修饰的常函数
const修饰的常函数 常函数常对象 常函数 成员函数后加const,称为常函数。常函数内部不可以修改成员变量。常函数内可以改变加了mutable修饰的成员变量。 code:#include <iostream>using namespace std;class Horse{public:int age 3;mutable string color …...
fail-safe 机制与 fail-fast 机制
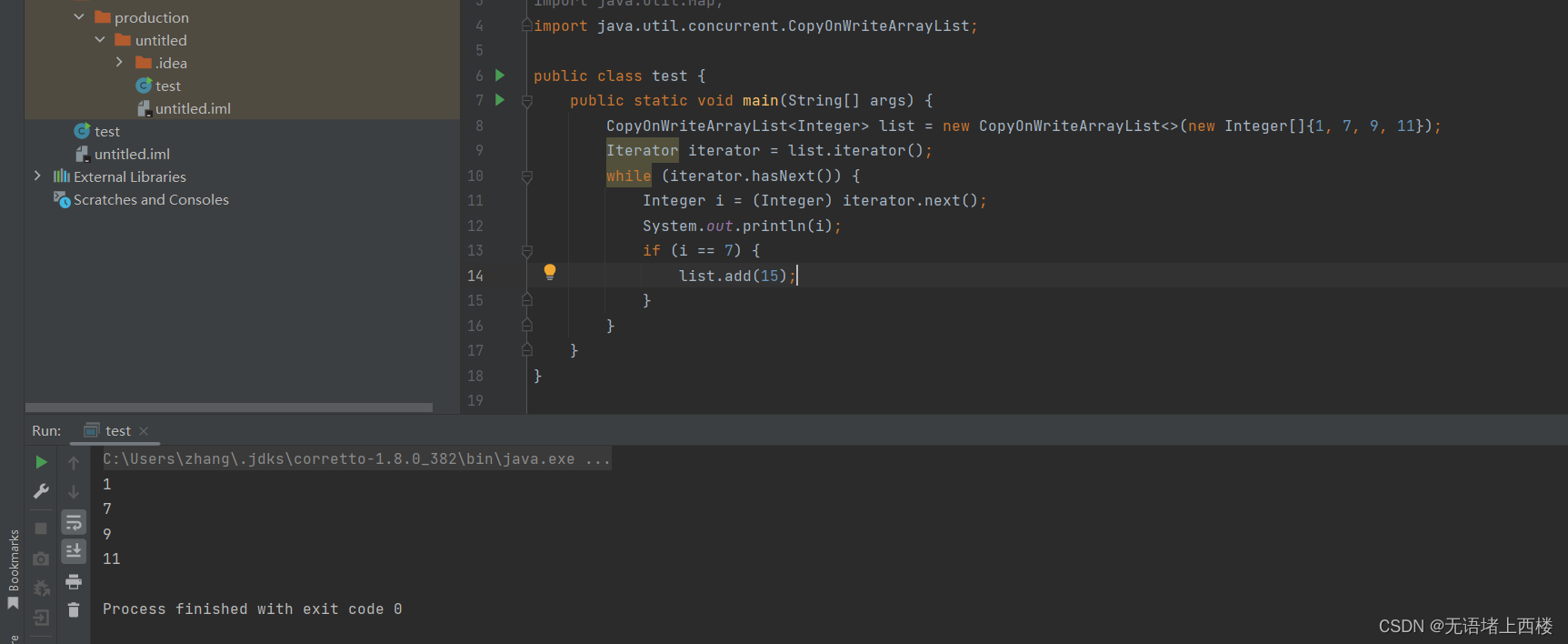
Fail-fast 表示快速失败,在集合遍历过程中,一旦发现容器中的数据被修改了,会立刻抛出 ConcurrentModificationException 异常,从而导致遍历失败,像这种情况 定义一个 Map 集合,使用 Iterator 迭代器进行数据…...

LLM 位置编码及外推
RoPE https://zhuanlan.zhihu.com/p/629681325 PI 位置插值(POSITION INTERPOLATION)显著改善RoPE的外推能力。你只需要对PT(pretraining)模型fine-turing最多1000步就能实现。PI是通过将线性的缩小了输入位置的索引使其匹配原始上下文窗口…...

第3章_瑞萨MCU零基础入门系列教程之开发环境搭建与体验
本教程基于韦东山百问网出的 DShanMCU-RA6M5开发板 进行编写,需要的同学可以在这里获取: https://item.taobao.com/item.htm?id728461040949 配套资料获取:https://renesas-docs.100ask.net 瑞萨MCU零基础入门系列教程汇总: ht…...

AI在医疗保健领域:突破界限,救治生命
文章目录 AI在医学影像分析中的应用AI在疾病预测和早期诊断中的作用个性化治疗和药物研发医疗数据管理和隐私保护未来展望 🎉欢迎来到AIGC人工智能专栏~AI在医疗保健领域:突破界限,救治生命 ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博…...

centos7安装kubernets集群
一、准备工作 准备三台虚拟机,centos7系统 二、系统配置 1. 修改主机名 # 三台机器都需要执行 hostnamectl set-hostname k8s-master hostnamectl set-hostname k8s-node1 hostnamectl set-hostname k8s-node22. 修改hosts文件 # 三台机器都需要执行 [rootk8s-…...
【多线程】线程安全与线程同步
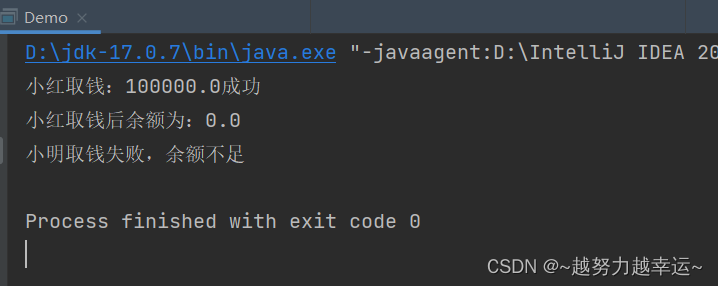
线程安全与线程同步 1.什么是线程安全问题? 多个线程同时操作同一个共享资源的时候,可能会出现业务安全问题 取钱的线程安全问题场景: 两个人他们有一个共同的账户,余额是10万元,如果两个人同时来取钱,…...

指针权限,new与delete,类与对象,函数模板,类模板的用法
指针权限 用法 void Print(const char* SecretPointer) {cout << "绝密指令为:";cout << SecretPointer << endl; }void Change(int& number, int* const FixedPointer) {cout << "更换站台数字为:";c…...

Unity——脚本与序列化
在介绍序列化之前,我们先来了解一下为什么要对数据进行序列化 数据序列化有以下几个主要的应用场景和目的: 1. 持久化存储:序列化可以将对象或数据结构转换为字节序列,使得其可以被存储在磁盘上或数据库中。通过序列化ÿ…...

NJ求职盘点
电子显示 集成电路 地平线 后摩智能 芯启源 自动驾驶 地平线 栖霞区兴智科技园 泊车、SLAM/3D算法工程师 https://wecruit.hotjob.cn/SU64819a4f2f9d2433ba8b043a/pb/social.html?currentPage1 后摩智能 栖霞区兴智科技园 视觉感知算法资深工程师 可以做自动驾驶前瞻性…...

01卡特兰数
卡特兰数跟排列组合很有关系,所以在看此文章前请掌握: 加法原理乘法原理A(m,n)计算公式及其原理C(m,n)计算公式及其原理 前言 今天您将会学习到基本的卡特兰数及其应用。 一、卡特兰数是什么? 卡特兰数(Catalan number࿰…...
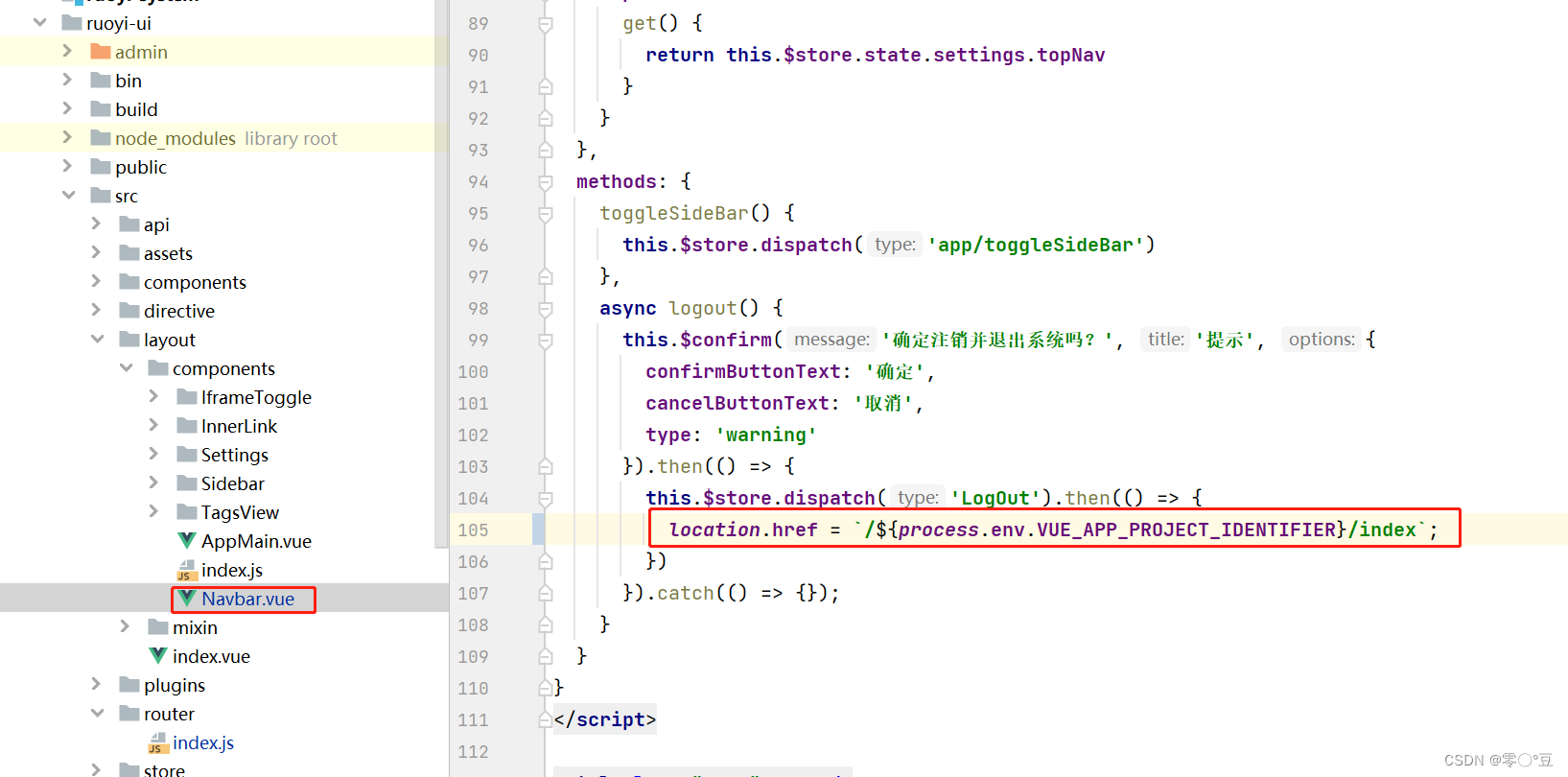
若依前端vue设置子路径
若依前端vue设置子路径 说明:本文档中以前后端分离版为例,版本为:3.8.6 一设置变量 在.env.development和.env.production 中定义一个变量如VUE_APP_PROJECT_IDENTIFIER # 项目标识字符 VUE_APP_PROJECT_IDENTIFIER admin二引用路径变量 ${process…...

Vue中使用pdf.js实现在线预览pdf文件流
以下是在Vue中使用pdf.js实现在线预览pdf文件流的步骤: 1. 安装pdf.js npm install pdfjs-dist2. 引入pdf.js 在需要使用的组件中,使用以下代码引入pdf.js: import pdfjsLib from pdfjs-dist3. 加载pdf文件流 使用pdf.js的getDocument()方…...

态、势、感、知与时空、关系
态势感知是一种通过收集、整合、分析和解释大量的时空数据,以获取关于特定领域、地区或事件的全面理解的过程。时空和关系在态势感知中扮演着非常重要的角色。 态:态指的是物体或系统所处的状态或状况。在不同的态下,物体或系统的性质、行为和…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...
