01卡特兰数
卡特兰数跟排列组合很有关系,所以在看此文章前请掌握:
- 加法原理
- 乘法原理
- A(m,n)计算公式及其原理
- C(m,n)计算公式及其原理
前言
今天您将会学习到基本的卡特兰数及其应用。
一、卡特兰数是什么?
卡特兰数(Catalan number)是组合数学中一种常出现于各种计数问题中的数列。其前几项为:1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
二、卡特兰数如何计算
设h(n)为catalan数的第n项,令h(0)=1,h(1)=1,catalan数满足递推式:
h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)*h(0) (n≥2)例如:h(2)=h(0)*h(1)+h(1)*h(0)=1*1+1*1=2
h(3)=h(0)*h(2)+h(1)*h(1)+h(2)*h(0)=1*2+1*1+2*1=5
另类递推式:
h(n)=h(n-1)*(4*n-2)/(n+1)h(n+1)=h(n) * (4*n + 2) / (n + 2)递推关系的解为:
h(n)=C(2n,n)/(n+1) (n=0,1,2,...)递推关系的另类解为:
h(n)=C(2n,n) - C(2n,n-1) (n=0,1,2,...)三、卡特兰的实际应用
1.思路分析
您可以先看这一题。
现在我们来思考这道题:
首先,我们设 f(n)=序列个数为n的出栈序列种数。(我们假定,最后出栈的元素为k,显然,k取不同值时的情况是相互独立的,也就是求出每种k最后出栈的情况数后可用加法原理,由于k最后出栈,因此,在k入栈之前,比k小的值均出栈,此处情况有f(k-1)种,而之后比k大的值入栈,且都在k之前出栈,因此有f(n-k)种方式,由于比k小和比k大的值入栈出栈情况是相互独立的,此处可用乘法原则,f(n-k)*f(k-1)种,求和便是Catalan递归式。)
首次出空之前第一个出栈的序数k将1~n的序列分成两个序列,其中一个是1~k-1,序列个数为k-1,另外一个是k+1~n,序列个数是n-k。
此时,我们若把k视为确定一个序数,那么根据乘法原理,f(n)的问题就等价于——序列个数为k-1的出栈序列种数乘以序列个数为n - k的出栈序列种数,即选择k这个序数的 f(n) =f(k-1) × f(n-k)。而k可以选1到n,所以再根据加法原理,将k取不同值的序列种数相加,得到的总序列种数为:f(n) = f(0)f(n-1) + f(1)f(n-2) + …… + f(n-1)f(0)。
2.我的打表代码
#include<bits/stdc++.h>
using namespace std;
long long a[18]={1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700};
int main(){int x;cin>>x;cout<<a[x-1]<<endl;return 0;
}四、AI说的话
1.AI对卡特兰数的评价
卡特兰数是一种非常重要的组合数学概念,它在许多领域都有广泛应用。下面是对卡特兰数的一些评价:
1. 卡特兰数可以表示组合问题和路径计数问题。
2. 卡特兰数的计算方法简单明了,可通过递推公式或生成函数求解。
3. 卡特兰数的性质丰富,涉及到二叉树、括号序列、山峰序列等多种组合结构。
4. 卡特兰数常被用于解决实际问题,如括号匹配、高维几何计算等。
5. 卡特兰数还具有一些意想不到的应用,如计算有限自动机、判断合法的棋盘布局等。
总之,卡特兰数作为组合数学中的重要概念,不仅具有理论意义,更有着实际应用价值。
2.AI解释卡特兰数的应用
卡特兰数是一类非常重要的数列,因为它们可以用于解决许多实际应用问题。以下是卡特兰数的一些应用:
-
括号序列:一个括号序列是由左右括号组成的字符串,例如 (()())。卡特兰数可以用于计算长度为n的括号序列的数量,以及其中合法的括号序列的数量。
-
凸多边形三角剖分:在凸多边形中,任何三角形的划分都可以由其对角线进行。卡特兰数可以用于计算划分凸多边形所需的对角线数量。
-
二叉树:卡特兰数也可以用于计算由n个节点构成的二叉树的数量。这里,每个节点不仅包含一个值,而且还包含指向其左子节点和右子节点的指针。
-
杨表:卡特兰数也可以用于计算n个数的杨表的数量,其中杨表是一种将n个数排列成不降序列的方案。
-
格路线:在一个n×n的网格上,从左下角到右上角的路径必须从每个格子的下方或右方穿过。卡特兰数可以用于计算这样的路径的数量。
-
栈的操作序列:假设我们有一个空栈,我们可以将n个数字插入该栈。卡特兰数可以用于计算所有n个数字的操作序列的数量,其中每个操作可以是“压入”或“弹出”。
-
电力分配:假设我们有n台发电机和n个城市,每台发电机都可以向多个城市提供电力。卡特兰数可以用于计算所有可能的电力分配方案。
总之,卡特兰数在组合数学中起着非常重要的作用,它们的应用广泛,不仅仅限于上述问题。
3.AI生成的卡特兰数C++代码
以下是使用C++语言生成卡特兰数的示例代码:
#include <iostream>
using namespace std;unsigned long int catalanDP(unsigned int n)
{// Table to store precomputed values of catalan numbersunsigned long int catalan[n + 1];// Initialize first two values in tablecatalan[0] = catalan[1] = 1;// Fill entries in catalan[] using DPfor (int i = 2; i <= n; i++){catalan[i] = 0;for (int j = 0; j < i; j++)catalan[i] += catalan[j] * catalan[i - j - 1];}// Return last entryreturn catalan[n];
}int main()
{for (int i = 0; i < 10; i++)cout << catalanDP(i) << " ";return 0;
}
此示例代码使用动态规划方法来计算卡特兰数,并使用循环生成前10个卡特兰数。
总结
以上就是今天要讲的内容。
相关文章:

01卡特兰数
卡特兰数跟排列组合很有关系,所以在看此文章前请掌握: 加法原理乘法原理A(m,n)计算公式及其原理C(m,n)计算公式及其原理 前言 今天您将会学习到基本的卡特兰数及其应用。 一、卡特兰数是什么? 卡特兰数(Catalan number࿰…...
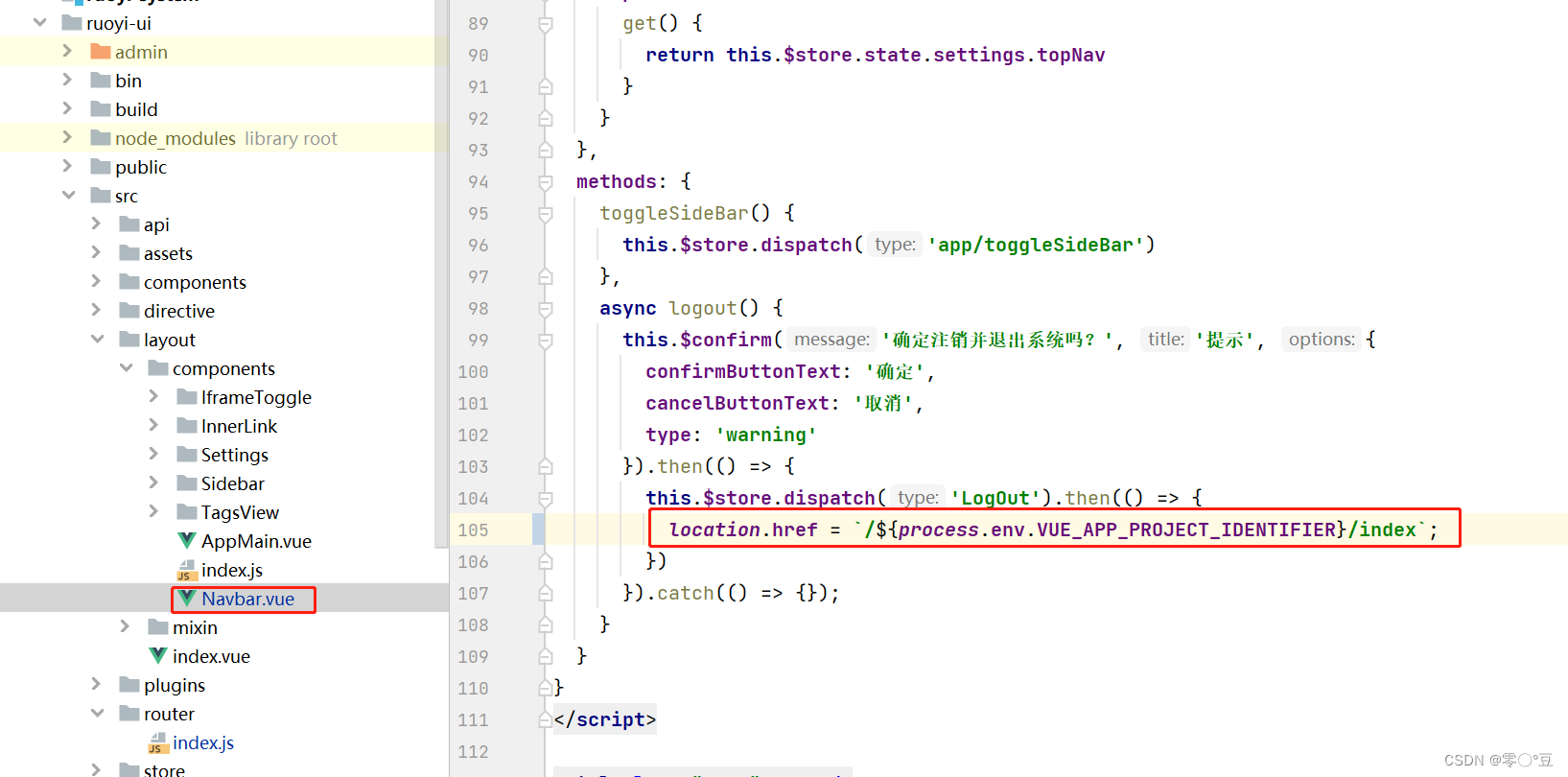
若依前端vue设置子路径
若依前端vue设置子路径 说明:本文档中以前后端分离版为例,版本为:3.8.6 一设置变量 在.env.development和.env.production 中定义一个变量如VUE_APP_PROJECT_IDENTIFIER # 项目标识字符 VUE_APP_PROJECT_IDENTIFIER admin二引用路径变量 ${process…...

Vue中使用pdf.js实现在线预览pdf文件流
以下是在Vue中使用pdf.js实现在线预览pdf文件流的步骤: 1. 安装pdf.js npm install pdfjs-dist2. 引入pdf.js 在需要使用的组件中,使用以下代码引入pdf.js: import pdfjsLib from pdfjs-dist3. 加载pdf文件流 使用pdf.js的getDocument()方…...

态、势、感、知与时空、关系
态势感知是一种通过收集、整合、分析和解释大量的时空数据,以获取关于特定领域、地区或事件的全面理解的过程。时空和关系在态势感知中扮演着非常重要的角色。 态:态指的是物体或系统所处的状态或状况。在不同的态下,物体或系统的性质、行为和…...
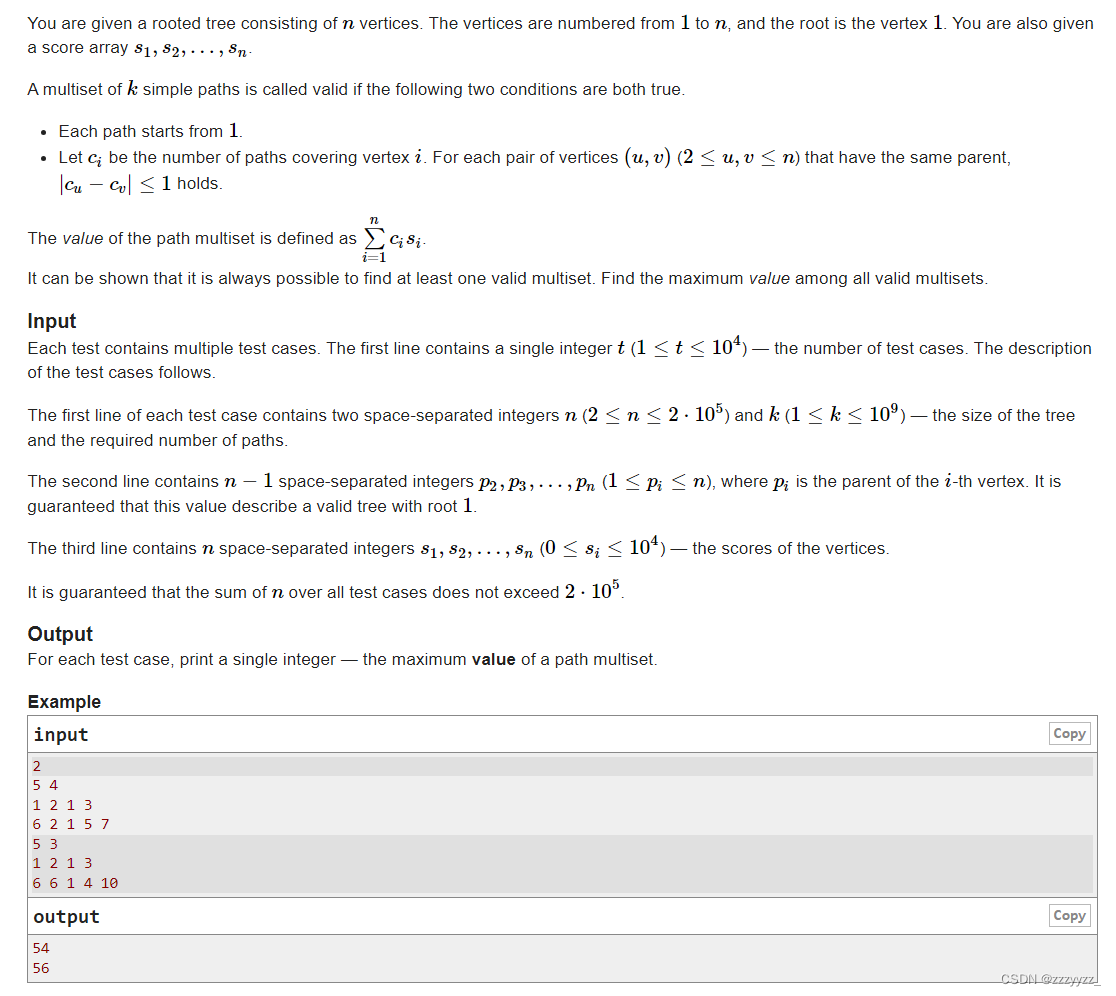
D. Paths on the Tree
Problem - 1746D - Codeforces 思路:先分析一下题意,根据第一条性质,每次只能够从1开始,而第二条性质则表明对于每个节点来说,经过这个节点的子节点的路径条数应该尽量均衡,最大值与最小值相差不能超过1&am…...

CocosCreator3.8研究笔记(九)CocosCreator 场景资源的理解
相信很多朋友都想知道, Cocos Creator 资源的定义? Cocos Creator 常见的资源包含哪些?Cocos Creator 资源的管理机制是什么样的? Cocos Creator 中所有继承自 Asset 的类型都统称资源 ,例如:Texture2D、Sp…...
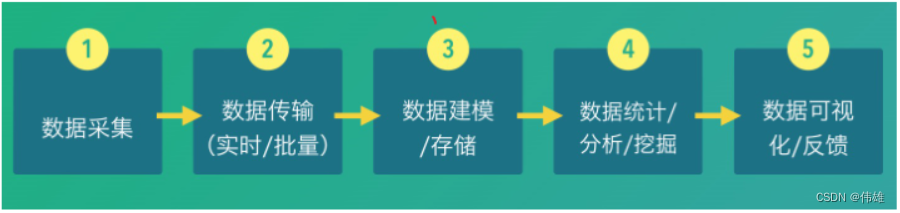
大数据课程L1——网站流量项目的概述整体架构
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解网站流量项目的案例概述; ⚪ 了解网站流量项目的数据埋点和采集; ⚪ 了解网站流量项目的整体架构; 一、网站流量项目概述 1. 背景说明 网站流量统计是改进网站服务的重要手段之一…...
提升数据库安全小技巧,使用SSH配合开源DBeaver工具连接数据库
title: 提升数据库安全小技巧,使用SSH配合开源DBeaver工具连接数据库 categories: 独立博客的方方面面 前段时间, 未来降低网址运行成本,搭了一套Mysql Docker 数据库, 包括外部链接,数据备份,数据导出,数据恢复一套解…...

信息安全技术概论-李剑-持续更新
图片和细节来源于 用户 xiejava1018 一.概述 随着计算机网络技术的发展,与时代的变化,计算机病毒也经历了从早期的破坏为主到勒索钱财敲诈经济为主,破坏方式也多种多样,由早期的破坏网络到破坏硬件设备等等 ,这也…...
java项目基于 SSM+JSP 的人事管理系统
java项目基于 SSMJSP 的人事管理系统 博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W,Csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 大家好,今天和大家聊的是 Java 基于 SSM 的人事管理系统。…...
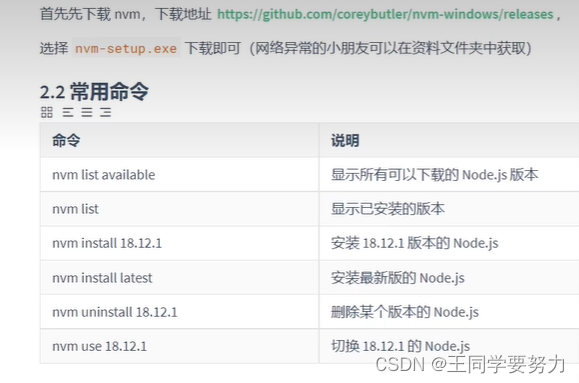
【Node.js】—基本知识点总结
【Node.js】—基本知识总结 一、命令行常用操作 二、Node.js注意点 Node.js中不能使用BOM和DOM操作 总结 三、Buffer buffer是一个类似于数组的对象,用于表示固定长度的字节序列buffer的本质是一段内存空间,专门用来处理二进制数据 特点:…...
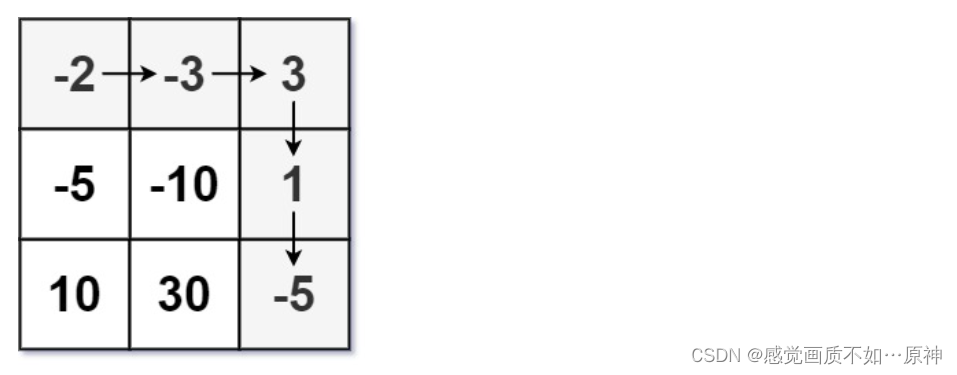
Leetcode.174 地下城游戏
题目链接 Leetcode.174 地下城游戏 hard 题目描述 恶魔们抓住了公主并将她关在了地下城 d u n g e o n dungeon dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公…...
python实现adb辅助点击屏幕工具
#!/usr/bin/env python # -*- coding: utf-8 -*-import re import os import time import subprocess import tkinter as tk from tkinter import messagebox from PIL import Image, ImageTk# 设置ADB路径(根据你的系统和安装路径进行调整) ADB_PATH C…...
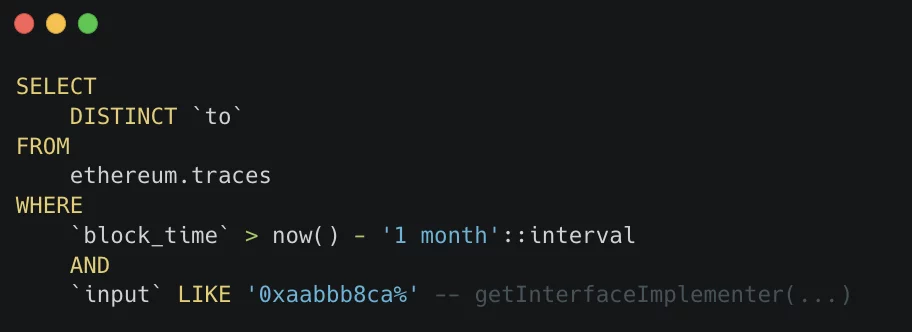
智能合约安全分析,针对 ERC777 任意调用合约 Hook 攻击
智能合约安全分析,针对 ERC777 任意调用合约 Hook 攻击 Safful发现了一个有趣的错误,有可能成为一些 DeFi 项目的攻击媒介。这个错误尤其与著名的 ERC777 代币标准有关。此外,它不仅仅是众所周知的黑客中常见的简单的重入问题。 这篇文章对 …...

nodejs 爬虫 axios 异步爬虫 教程 【一】
axios 自定义headers axios.defaults.headers.common["User-Agent"] "Googlebot/2.1 (http://www.google.com/bot.html)"; 运行环境: node :v18 const axios require("axios"); axios.defaults.headers.common["U…...
)
Swift学习笔记三(Dictionary 篇)
1 Dictionary 概念 字典储存无序的互相关联的同一类型的键和同一类型的值的集合。字典类型的全写方式 Dictionary<Key, Value>,简写方式 [Key: Value],建议使用简写方式。字典的 key 必须是可哈希的。 2 Dictionary创建 2.1 初始器创建方式 2.2 …...

javax.mail 遇到501 mail from address must be same as authorization user 的問題
使用不同的兩個帳戶发送email时,第一个账户可以发送成功,但到第二个账户的时候就报出了501 mail from address must be same as authorization user的错误。 具体代码如下: import java.util.Date; import java.util.List; import java.util.…...
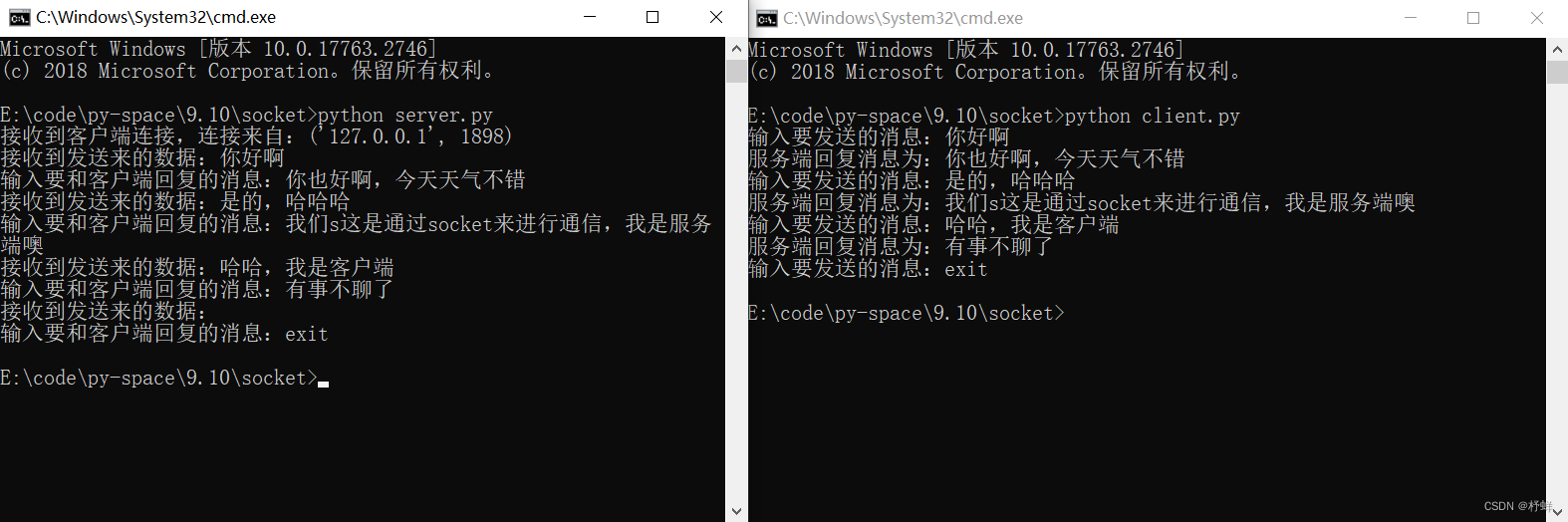
【Python】网络编程
Socket Socket (简称 套接字)是进程之间通信一个工具,进程之间想要进行网络通信需要socket。Socket负责进程之间的网络数据传输,好比数据的搬运工。 客户端和服务端 2个进程之间通过Socket进行相互通讯,就必须有服务端和客户端 Socket服务…...

客户端开发常用框架
在Unity游戏开发中,客户端常用的框架包括以下几种: 1.Unity的网络框架:Unity自带了网络框架,包括Unity Networking、Unity Matchmaker和Unity Remote等。这些框架可以帮助我们进行游戏的联机对战、排行榜、跨平台等功能的设计和实…...

数据分析综述
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
