【C++入门到精通】C++入门 ——搜索二叉树(二叉树进阶)

阅读导航
- 前言
- 一、搜索二叉树简介
- 1. 概念
- 2. 基本操作
- ⭕搜索操作
- 🍪搜索操作基本代码(非递归)
- ⭕插入操作
- 🍪插入操作基本代码(非递归)
- ⭕删除操作
- 🍪删除操作基本代码(非递归)
- 二、搜索二叉树的实现
- 1. 非递归实现
- 2. 递归实现
- 三、搜索二叉树的应用
- 1. K模型
- 2. KV模型
- 四、搜索二叉树的性能分析
- 总结
- 温馨提示
前言
前面我们讲了C语言的基础知识,也了解了一些初阶数据结构,并且讲了有关C++的命名空间的一些知识点以及关于C++的缺省参数、函数重载,引用 和 内联函数也认识了什么是类和对象以及怎么去new一个 ‘对象’ ,也了解了C++中的模版,以及学习了几个STL的结构也相信大家都掌握的不错,接下来博主将会带领大家继续学习有关C++比较重要的知识点——搜索二叉树(二叉树进阶) 。下面话不多说坐稳扶好咱们要开车了😍
一、搜索二叉树简介
1. 概念
搜索二叉树,也称为二叉搜索树(Binary Search Tree,BST),是一种二叉树的特殊形式。它满足以下条件:
- 有序性:对于任意节点,其左子树中的所有节点的值都小于该节点的值,右子树中的所有节点的值都大于该节点的值。
- 唯一性:每个节点的值唯一,不存在相同值的节点。
- 递归结构:整个树的结构由左子树、右子树和根节点组成,其中左子树和右子树也是搜索二叉树。

2. 基本操作
⭕搜索操作
- 从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
- 最多查找高度次,走到到空,还没找到,这个值不存在。
在搜索二叉树中查找一个特定值的操作很简单。从根节点开始,如果目标值等于当前节点的值,则找到了目标节点;如果目标值小于当前节点的值,则在左子树中继续搜索;如果目标值大于当前节点的值,则在右子树中继续搜索。通过递归或循环,可以在树中进行有效的搜索。
🍪搜索操作基本代码(非递归)
bool Find(const K& key)
{Node* ret = _root;// 循环查找节点,直到找到与 key 匹配的节点或遍历完整个树while (ret){// 如果当前节点的键值大于 key,继续在左子树中查找if (ret->_key > key){ret = ret->_left;}// 如果当前节点的键值小于 key,继续在右子树中查找else if (ret->_key < key){ret = ret->_right;}// 如果当前节点的键值等于 key,找到匹配节点,返回 trueelse{return true;}}// 遍历完整个树仍未找到匹配节点,返回 falsereturn false;
}
该函数接收一个键值 key,表示需要查找的值。函数首先将根节点指针 _root 赋值给临时指针变量 ret。然后通过循环遍历树进行查找,直到找到与 key 匹配的节点或遍历完整个树。
在循环中,根据当前节点的键值与 key 的比较结果决定下一步的查找方向:
- 如果当前节点的键值大于 key,继续在左子树中查找;
- 如果当前节点的键值小于 key,继续在右子树中查找;
- 如果当前节点的键值等于 key,找到匹配节点,返回 true。
当遍历完整个树仍未找到匹配节点时,返回 false 表示未找到。
⭕插入操作
- 树为空,则直接新增节点,赋值给root指针
- 树不空,按二叉搜索树性质查找插入位置,插入新节点
要向搜索二叉树中插入新节点,需要找到合适的位置。从根节点开始,与当前节点的值比较,根据值的大小决定是在左子树还是右子树中进行插入。重复这个过程,直到找到一个空的位置,然后将新节点插入其中。
🍪插入操作基本代码(非递归)
bool Insert(const K& key)
{// 如果根节点为空,直接将 key 作为根节点创建if (_root == nullptr){_root = new Node(key);return true;}Node* ret = _root;Node* parent = nullptr;// 找到 key 应该插入的位置while (ret){// 如果 key 小于当前节点的键值,继续在左子树查找if (key < ret->_key){parent = ret;ret = ret->_left;}// 如果 key 大于当前节点的键值,继续在右子树查找else if (key > ret->_key){parent = ret;ret = ret->_right;}// 如果 key 已经存在于树中,返回 falseelse{return false;}}// 创建新节点,将其插入正确的位置Node* cur = new Node(key);if (parent->_key > key){parent->_left = cur;}else{parent->_right = cur;}return true;
}
该函数接收一个键值 key,表示需要插入的值。函数首先判断根节点是否为空,如果为空,则直接将 key 作为根节点插入并返回 true。否则,使用循环找到 key 需要插入的位置:
- 如果 key 小于当前节点的键值,继续在左子树查找;
- 如果 key 大于当前节点的键值,继续在右子树查找;
- 如果 key 等于当前节点的键值,则说明值已经存在于树中,返回 false。
当找到正确的位置时,创建一个新的节点 cur,并将其插入到树中。具体实现如下:
- 如果 key 小于父亲节点的键值,将 cur 插入父节点的左子树中;
- 如果 key 大于父亲节点的键值,将 cur 插入父节点的右子树中。
插入完成后,返回 true 表示插入成功。
⭕删除操作
删除节点的过程相对复杂,需要考虑不同的情况,主要分为以下三种情况处理:
-
删除节点没有子节点(叶子节点):直接将该节点删除即可,将其父节点指向它的指针置为 NULL。
-
删除节点有一个子节点:将该节点的子节点替代该节点的位置,将该节点的父节点指向它的指针直接指向子节点。
-
删除节点有两个子节点:这是最复杂的情况。需要找到该节点的后继节点或者前驱节点来替代该节点的位置。后继节点是指比当前节点大的最小节点,前驱节点是指比当前节点小的最大节点。
-
找到后继节点的方法是:在当前节点的右子树中找到值最小的节点,即右子树中最左边的节点,然后将其值复制到待删除节点的位置,再删除后继节点。
-
找到前驱节点的方法是:在当前节点的左子树中找到值最大的节点,即左子树中最右边的节点,然后将其值复制到待删除节点的位置,再删除前驱节点。
-
🍪删除操作基本代码(非递归)
bool Erase(const K& key)
{Node* ret = _root;Node* parent = nullptr;// 循环查找节点,直到找到匹配的节点或遍历完整个树while (ret){// 如果 key 小于当前节点的键值,继续在左子树查找if (key < ret->_key){parent = ret;ret = ret->_left;}// 如果 key 大于当前节点的键值,继续在右子树查找else if (key > ret->_key){parent = ret;ret = ret->_right;}// 如果找到匹配的节点else{// 删除节点// 1. 如果当前节点的左子树为空if (ret->_left == nullptr){// 如果是根节点if (_root->_key == key){Node* tmp = _root;_root = _root->_right;delete tmp;return true;}else{// 如果是父节点的左子节点if (parent->_left == ret){parent->_left = ret->_right;}// 如果是父节点的右子节点else{parent->_right = ret->_right;}delete ret;}}// 2. 如果当前节点的右子树为空else if (ret->_right == nullptr){// 如果是根节点if (_root->_key == key){Node* tmp = _root;_root = _root->_left;delete tmp;return true;}else{// 如果是父节点的左子节点if (parent->_left == ret){parent->_left = ret->_left;}// 如果是父节点的右子节点else{parent->_right = ret->_left;}delete ret;}}// 3. 如果当前节点的左右子树都不为空else{// 找到右子树中最小的节点,用来替代当前节点Node* pminRight = ret;Node* minRight = ret->_right;while (minRight->_left){pminRight = minRight;minRight = minRight->_left;}// 将右子树中最小节点的值赋给当前节点,并删除最小节点ret->_key = minRight->_key;if (pminRight->_left == minRight){pminRight->_left = minRight->_right;}else{pminRight->_right = minRight->_right;}delete minRight;}return true;}}// 遍历完整个树仍未找到匹配节点,返回 falsereturn false;
}
该函数接收一个键值 key,表示需要删除的值。函数首先将根节点指针 _root 赋值给临时指针变量 ret,并初始化父节点指针 parent 为 nullptr。然后通过循环遍历树进行查找,直到找到与 key 匹配的节点或遍历完整个树。
在循环中,根据待删除节点的键值与 key 的比较结果决定下一步的查找方向:
- 如果 key 小于当前节点的键值,继续在左子树中查找;
- 如果 key 大于当前节点的键值,继续在右子树中查找;
- 如果当前节点的键值等于 key,找到匹配节点,并执行删除操作。
删除操作分为以下三种情况:
- 如果当前节点的左子树为空:将当前节点的右子树链接到父节点的对应位置,并删除当前节点。
- 如果当前节点的右子树为空:将当前节点的左子树链接到父节点的对应位置,并删除当前节点。
- 如果当前节点的左右子树都不为空:需要找到当前节点右子树中最小的节点(即右子树的最左下角节点),将该节点的值赋给当前节点,然后删除最小节点。
在执行删除操作时,可能存在以下两种特殊情况:
- 如果当前节点是根节点:需要更新
_root指针,让其指向新的根节点。 - 如果当前节点是某个节点的左子节点或右子节点:需要将该节点的父节点链接到删除节点的子节点,与该节点相邻的子树会被删除,然后释放删除节点的内存。
最后,如果遍历整个树仍未找到匹配节点,说明该节点不存在,函数返回 false。
二、搜索二叉树的实现
1. 非递归实现
namespace yws
{
template<class K>struct BSTreeNode{// 二叉搜索树节点的定义BSTreeNode(const K& key): _left(nullptr), _right(nullptr), _key(key){}BSTreeNode<K>* _left; // 左子节点指针BSTreeNode<K>* _right; // 右子节点指针K _key; // 节点存储的键值};template<class K>class BSTree{typedef BSTreeNode<K> Node;public://构造BSTree():_root(nullptr){}//拷贝构造BSTree(const BSTree<K>& t){_root = Copy(t._root);}//赋值构造BSTree<K>& operator=(BSTree<K> t){std::swap(_root, t._root);return *this;}//析构~BSTree(){Destory(_root);}bool Insert(const K& key){// 如果根节点为空,直接将 key 作为根节点创建if (_root == nullptr){_root = new Node(key);return true;}Node* ret = _root;Node* parent = nullptr;// 找到 key 应该插入的位置while (ret){// 如果 key 小于当前节点的键值,继续在左子树查找if (key < ret->_key){parent = ret;ret = ret->_left;}// 如果 key 大于当前节点的键值,继续在右子树查找else if (key > ret->_key){parent = ret;ret = ret->_right;}// 如果 key 已经存在于树中,返回 falseelse{return false;}}// 创建新节点,将其插入正确的位置Node* cur = new Node(key);if (parent->_key > key){parent->_left = cur;}else{parent->_right = cur;}return true;}bool Find(const K& key){Node* ret = _root;// 循环查找节点,直到找到与 key 匹配的节点或遍历完整个树while (ret){// 如果当前节点的键值大于 key,继续在左子树中查找if (ret->_key > key){ret = ret->_left;}// 如果当前节点的键值小于 key,继续在右子树中查找else if (ret->_key < key){ret = ret->_right;}// 如果当前节点的键值等于 key,找到匹配节点,返回 trueelse{return true;}}// 遍历完整个树仍未找到匹配节点,返回 falsereturn false;}bool Erase(const K& key){Node* ret = _root;Node* parent = nullptr;// 循环查找节点,直到找到匹配的节点或遍历完整个树while (ret){// 如果 key 小于当前节点的键值,继续在左子树查找if (key < ret->_key){parent = ret;ret = ret->_left;}// 如果 key 大于当前节点的键值,继续在右子树查找else if (key > ret->_key){parent = ret;ret = ret->_right;}// 如果找到匹配的节点else{// 删除节点// 1. 如果当前节点的左子树为空if (ret->_left == nullptr){// 如果是根节点if (_root->_key == key){Node* tmp = _root;_root = _root->_right;delete tmp;return true;}else{// 如果是父节点的左子节点if (parent->_left == ret){parent->_left = ret->_right;}// 如果是父节点的右子节点else{parent->_right = ret->_right;}delete ret;}}// 2. 如果当前节点的右子树为空else if (ret->_right == nullptr){// 如果是根节点if (_root->_key == key){Node* tmp = _root;_root = _root->_left;delete tmp;return true;}else{// 如果是父节点的左子节点if (parent->_left == ret){parent->_left = ret->_left;}// 如果是父节点的右子节点else{parent->_right = ret->_left;}delete ret;}}// 3. 如果当前节点的左右子树都不为空else{// 找到右子树中最小的节点,用来替代当前节点Node* pminRight = ret;Node* minRight = ret->_right;while (minRight->_left){pminRight = minRight;minRight = minRight->_left;}// 将右子树中最小节点的值赋给当前节点,并删除最小节点ret->_key = minRight->_key;if (pminRight->_left == minRight){pminRight->_left = minRight->_right;}else{pminRight->_right = minRight->_right;}delete minRight;}return true;}}// 遍历完整个树仍未找到匹配节点,返回 falsereturn false;}protected:Node* Copy(Node* root){if (root == nullptr){return nullptr;}Node newnode = new Node(root->_key);newnode->_left = Copy(root->_left);newnode->_right = Copy(root->_right);return newnode;}void Destory(Node*& root){if (root == nullptr)return;Destory(root->_right);Destory(root->_left);delete root;root = nullptr;}}private:Node* _root = nullptr;};
}
2. 递归实现
namespace yws
{template<class K>struct BSTreeNode{BSTreeNode(const K& key): _left(nullptr), _right(nullptr), _key(key){}BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;};template<class K>class BSTree{typedef BSTreeNode<K> Node;public://构造BSTree():_root(nullptr){}//拷贝构造BSTree(const BSTree<K>& t){_root = Copy(t._root);}//赋值构造BSTree<K>& operator=(BSTree<K> t){std::swap(_root, t._root);return *this;}//析构~BSTree(){Destory(_root);}void Inorder() // 中序遍历{_Inorder(_root);cout << endl;}//递归版本实现bool FindR(const K& key){return _FindR(_root, key);}bool InsertR(const K& key){return _InsertR(_root, key);}bool EraseR(const K& key){return _EraseR(_root, key);}protected:Node* Copy(Node* root){if (root == nullptr){return nullptr;}Node newnode = new Node(root->_key);newnode->_left = Copy(root->_left);newnode->_right = Copy(root->_right);return newnode;}void Destory(Node*& root){if (root == nullptr)return;Destory(root->_right);Destory(root->_left);delete root;root = nullptr;}void _Inorder(Node* root){if (root == nullptr){return;}_Inorder(root->_left);cout << root->_key << ' ';_Inorder(root->_right);}bool _FindR(Node* root, const K& key){if (root == nullptr){return false;}if (key < root->_key){_FindR(root->_left, key);}else if (key > root->_key){_FindR(root->_right, key);}else{return true;}}bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (key < root->_key){_InsertR(root->_left, key);}else if (key > root->_key){_InsertR(root->_right, key);}else{return false;}}bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}if (key > root->_key){return _EraseR(root->_right, key);}else if (key < root->_key){return _EraseR(root->_left, key);}else{//开始删除Node* del = root;//1.左节点为空if (root->_left == nullptr){root = root->_right;}//2.右节点为空else if (root->_right == nullptr){root = root->_left;}//3.左右节点都不为空else{//找右树的最小节点,代替Node* minRight = root->_right;while (minRight->_left){minRight = minRight->_left;}root->_key = minRight->_key;return _EraseR(root->_right, root->_key);}delete del;return true;}}private:Node* _root = nullptr;};
}三、搜索二叉树的应用
1. K模型
K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。因此,K模型对于不需要复杂数据处理功能的应用来说是一种轻量级的数据管理方案。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:
- 以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树。
- 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
2. KV模型
KV模型:每一个关键码key,都有与之对应的值Value,即 <Key, Value> 的键值对。该种方式在现实生活中非常常见
假设有一个存储学生信息的系统,每个学生信息仅包括学生的唯一ID和学生的姓名。这种情况下,我们可以使用K模型进行存储,其中学生的ID作为key,学生姓名作为value。
如下所示是几个学生的数据:
| 学生ID | 学生姓名 |
|---|---|
| 1001 | 张三 |
| 1002 | 李四 |
| 1003 | 王五 |
使用KV模型存储这些数据时,只需要记录学生ID作为key,对应的学生姓名作为value。例如,使用搜索二叉树来存储学生信息,可以根据学生ID快速查找到对应的学生姓名。这个例子展示了如何将KV模型与搜索二叉树结合,实现数据存储和检索的需求。
当需要查询某个学生的姓名时,只需要在二叉树中查找对应的学生ID,然后返回该学生的姓名即可。
四、搜索二叉树的性能分析
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:

最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为: l o g 2 N log_2 N log2N
最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为: N 2 \frac{N}{2} 2N
如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插入关键码,二叉搜索树的性能都能达到最优?那么我们后面的AVL树和红黑树就可以完美解决上面的问题了。
总结
搜索二叉树是一种常用的数据结构,用于存储和检索数据。搜索二叉树的应用,包括K模型和KV模型。K模型指的是只存储键而不存储关联值的数据模型。KV模型则是使用键值对来存储和访问数据的一种模型,可以用搜索二叉树实现。
最后,搜索二叉树的性能取决于树的平衡程度,理想情况下的时间复杂度为O(log n),但如果树不平衡,性能会下降至O(n)。为了保持树的平衡,可以采用平衡二叉树的变种,如红黑树或AVL树。
综上所述,搜索二叉树是一种重要的数据结构,具有广泛的应用。了解搜索二叉树的基本操作、实现方法和性能分析,对于合理选择和使用数据结构,提高数据操作效率具有重要意义。
温馨提示
感谢您对博主文章的关注与支持!另外,我计划在未来的更新中持续探讨与本文相关的内容,会为您带来更多关于C++以及编程技术问题的深入解析、应用案例和趣味玩法等。请继续关注博主的更新,不要错过任何精彩内容!
再次感谢您的支持和关注。期待与您建立更紧密的互动,共同探索C++、算法和编程的奥秘。祝您生活愉快,排便顺畅!

相关文章:

【C++入门到精通】C++入门 ——搜索二叉树(二叉树进阶)
阅读导航 前言一、搜索二叉树简介1. 概念2. 基本操作⭕搜索操作🍪搜索操作基本代码(非递归) ⭕插入操作🍪插入操作基本代码(非递归) ⭕删除操作🍪删除操作基本代码(非递归࿰…...

学成在线-网站搭建
文章目录 代码素材来自b站pink老师 <!DOCTYPE html> <html lang="en"> <head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scale=1.0"><title>学成在线首…...
stm32同芯片但不同flash工程更换Device出现报错
目录 1. 问题描述2. 解决方案 1. 问题描述 stm32同芯片但不同flash工程更换Device出现报错 2. 解决方案 更换Device,我是从ZE换为C8: 把这个从HD更换为MD 解决!...

Element UI实现每次只弹出一个Message消息提示
前言 在开发Web应用程序时,我们经常需要使用消息提示来向用户展示重要信息。Element UI提供了一个方便易用的组件——Message,可以用于显示各种类型的消息提示。 然而,默认情况下,当多个消息提示同时触发时,它们会依…...

「网页开发|前端开发|Vue」04 快速掌握开发网站需要的Vue基础知识
本文主要介绍使用Vue进行前端开发的一些必备知识,比如:Vue应用实例,Vue的组件概念,模板语言和模板语法,计算属性,路由配置等等。 文章目录 本系列前文传送门前言一、Vue实例:项目入口二、模板语…...

解决Redis分布式锁主从架构锁失效问题的终极方案 含面试题
面试题分享 2023最新面试合集链接 2023大厂面试题PDF 面试题PDF版本 java、python面试题 项目实战:AI文本 OCR识别最佳实践 AI Gamma一键生成PPT工具直达链接 玩转cloud Studio 在线编码神器 玩转 GPU AI绘画、AI讲话、翻译,GPU点亮AI想象空间 史上最全文档AI绘画stab…...
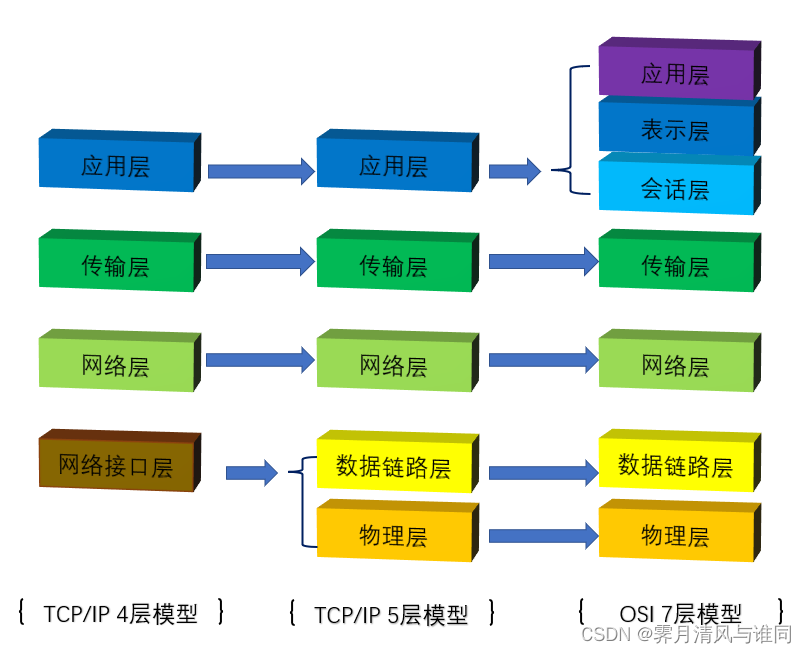
建站系列(三)--- 网络协议
目录 相关系列文章前言一、定义二、术语简介三、协议的组成要素四、网络层次划分五、常见网络协议划分六、常用协议介绍(一)TCP/IP(二)HTTP协议(超文本传输协议)(三)SSH协议 相关系列…...

jetson orin nx无显示器启动
sudo apt-get install xserver-xorg-core-hwe-18.04 sudo apt-get install xserver-xorg-video-dummy在 /usr/share/X11/xorg.conf.d/ 中添加 xorg.conf 文件。 Section "Monitor"Identifier "Monitor0"HorizSync 28.0-80.0VertRefresh 48.0-75.0Modeline…...

【APUE】标准I/O库
目录 1、简介 2、FILE对象 3、打开和关闭文件 3.1 fopen 3.2 fclose 4、输入输出流 4.1 fgetc 4.2 fputc 4.3 fgets 4.4 fputs 4.5 fread 4.6 fwrite 4.7 printf 族函数 4.8 scanf 族函数 5、文件指针操作 5.1 fseek 5.2 ftell 5.3 rewind 6、缓冲相关 6.…...

es6---模块化
main.js import { bar } from "./module1"; import module2 from "./module2"; bar() module2()module1.js // 多变量导出,导入变量需要变量名一对一映射 export const module1module1 export function bar(params) {console.log(module1) }m…...
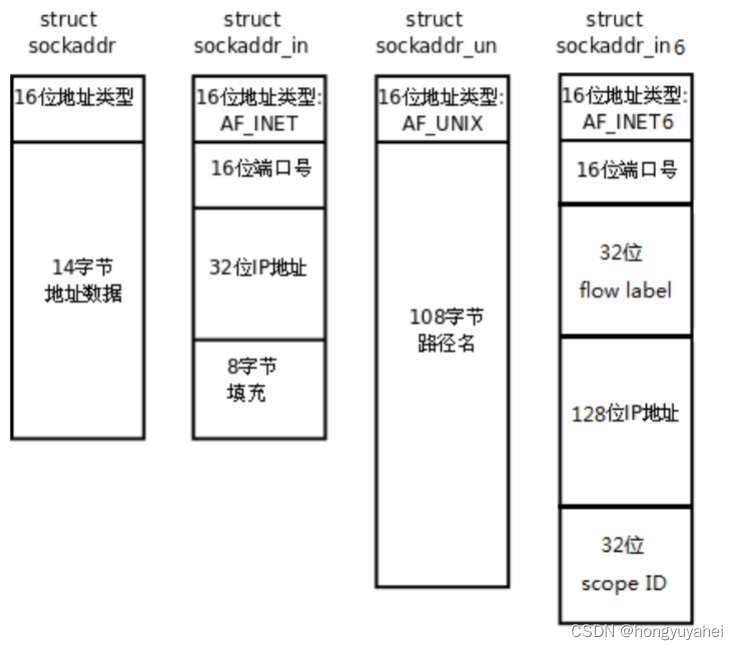
【项目 计网12】4.32UDP通信实现 4.33广播 4.34组播 4.35本地套接字通信
文章目录 4.32UDP通信实现udp_client.cudp_server.c 4.33广播bro_server.cbro_client.c 4.34组播multi_server.cmulti_client.c 4.35本地套接字通信ipc_server.cipc_client.c 4.32UDP通信实现 udp_client.c #include <stdio.h> #include <stdlib.h> #include <…...

创建简单的 Docker 数据科学映像
推荐:使用NSDT场景编辑器快速搭建3D应用场景 为什么选择 Docker for Data Science? 作为一名数据科学家,拥有一个标准化的便携式分析和建模环境至关重要。Docker 提供了一种创建可重用和可共享的数据科学环境的绝佳方法。在本文中ÿ…...

angualr:CSS一个div内两个子元素的高度自适应
问题: 如题 参考: CSS一个div内两个子元素的高度自适应-腾讯云开发者社区-腾讯云...
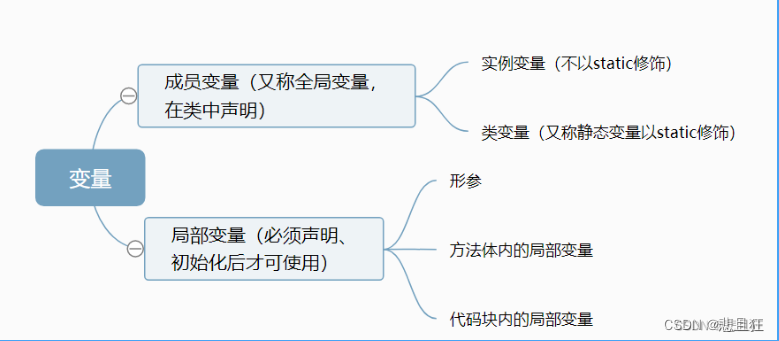
Java基础之static关键字
目录 静态的特点第一章、静态代码块第二章、静态属性第三章、静态方法调用静态方法时静态方法中调用非静态方法时 第四章、static关键字与其他关键字 友情提醒 先看文章目录,大致了解文章知识点结构,点击文章目录可直接跳转到文章指定位置。 静态的特点…...

iPhone 15 Pro有5项重大设计升级,让iPhone 15看起来很无聊
距离苹果9月份的发布会还有不到一周的时间,我们很快就会第一次看到iPhone 15系列。源源不断的传言表明,这一代人将对大多数机型进行另一次增量更新,这对那些想换iPhone 14或更旧手机的人来说是个坏消息。 但这一次的高端选择,iPh…...

xCode14.3.1运行MonkeyDev出现“Executable Not Found“的解决办法
安装MonkeyDev遇到的坑 环境:Xcode Version 14.3.1 (14E300c) 错误提示 is not a valid path to an executable file. 报错 /Users/xxxx//Library/Developer/Xcode/DerivedData/MonTest-ccparhdyzjuqhjdergwrngpfwwoh/Build/Products/Debug-iphoneos/MonTest.app…...
C# Emgu.CV+Tesseract实现识别图像验证码
效果图,简单的还行,复杂的。。。拉跨 懒得写讲解了,全部源码直接上吧 /// <summary>/// 验证码识别/// </summary>public partial class FrmCodeIdentify : FrmBase{private string _filePath;// 原图像Image<Bgr, byte> …...

ORACLE 11.2.0.4 RAC Cluster not starting cssd with Cannot get GPnP profile
最近,处理一次oracle 11.2.0.4 rac cluster由于cssd无法启动,导致集群一个节点的CRS集群无法正常启动的故障。原本,计划变更是从ASM剔除磁盘,解除存储到数据库服务器的映射;磁盘已经成功从ASM剔除,也已经成…...

Converting Phase Noise to Random Jitter(Cycle-to-Cycle)
借用Phase Noise to Random Jitter(Period)的转换过程推导了Cycle to Cycle random Jitter,一般展频时钟调制,用来评估相邻周期的随机抖动。...

HashMap知识总结
HashMap: 1. 扰动函数hash值右移16位与原hash值做异或运算得出的新hash值散列程度高. 2. 负载因子0.75,就是说一个数组初始化new HashMap(17)容量会比17最小2的n次方大,就是32,想要已空间换时间,就是负载因子小于0.75这样的话hash冲突更低,但是扩容频率更高.3 扩容,jdk…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
