数据结构_ 堆结构与堆排序(c++ 实现 + 完整代码 )
堆结构与堆排序
文章目录
- 堆结构与堆排序
- 引入堆
- 堆结构所满足的数学特性
- 准备代码
- ----------- 往堆中插入元素
- ----------- 删除堆顶
- 堆排序构建
- 完整代码及测试
- 动态分配版本
- 非动态版本
引入堆
-
二叉树
具有左孩子与右孩子的最普通的二叉树。 -
满二叉树
特殊的二叉树:每个节点如果有孩子则一定同时具有左孩子与右孩子。
满二叉树的条件:
- 要么有两个孩子,要么没有孩子
- 叶子节点在同一层
满二叉树有如下规律:
如果层数为n
第n层节点数 一定为 2^(n-1)
整颗树节点数 为 2^n - 1
-
完全二叉树
能够使得满二叉树 从 下边和右边开始删节点的 二叉树 , 满足从右往左 从下往上删除 (和 阅读顺序 相反)-
满二叉树一定是完全二叉树
-
完全二叉树不一定是满二叉树
-
-
堆
堆是有序的完全二叉树。
父子之间必须有序,父大于子或者子大于父,同层兄弟之间不用管
- 父大于子:最大堆(大顶堆)
- 子大于父:最小堆(小顶堆)
堆结构所满足的数学特性
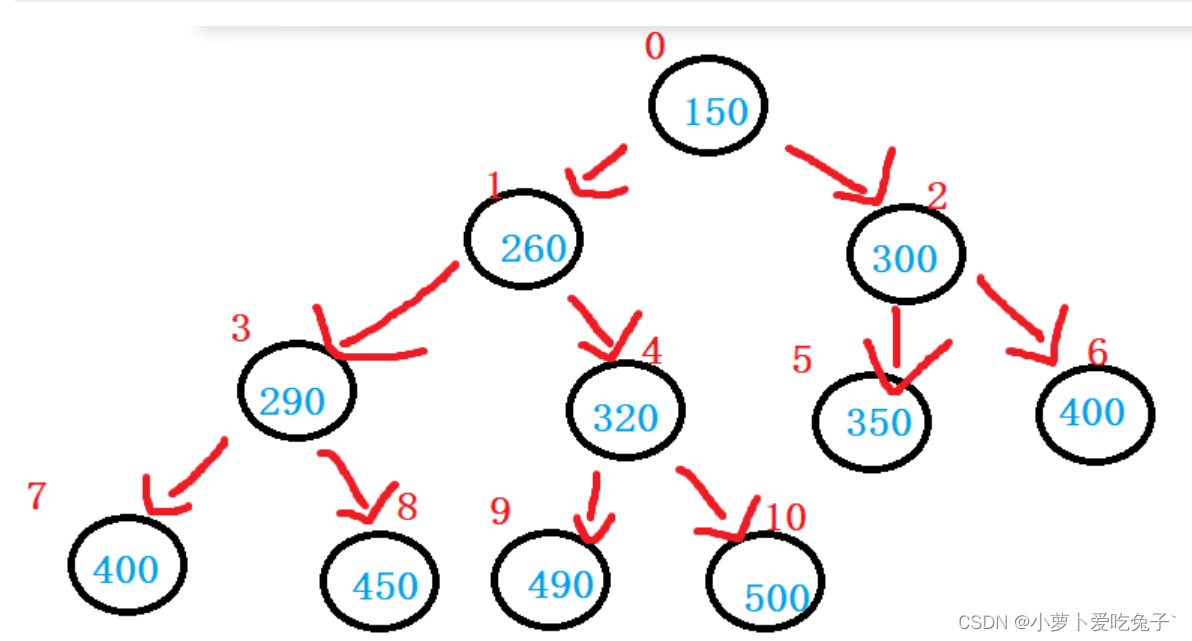
下标关系:
-
150 的 下标为 0 ,260 的下标为1,290的下标为3,400的下标为7。共同点:都是父节点的左孩子,父节点的下标*2+1=左孩子的下标
-
150的下标为0,300的下标为2,400的下标为6;260的下标为1,320的下标为4,500的下标为10。共同点:都是父节点的右孩子,父节点的下标*2+2=右孩子的下标
-
相反,已知400的下标为7,则290的下标为3,260的下标为1。共同点:已知左孩子的下标,(左孩子下标-1)/2得到父节点的下标
-
已知500的下标为10,320的下标为4,260 的下标为1。共同点:已知右孩子的下标,(右孩子下标-2)/2得到父节点的下标
总结:
父亲推孩子:
已知父节点下标为N
左孩子下标为:2*N + 1右孩子下标为:2*N + 2
孩子反推父亲:
已知左孩子下标为M 父节点下标为: (M-1)/2
已知右孩子下标为M 父节点下标为: (M-2)/2已知孩子下标为M 父节点下标为: (M-1)/2
准备代码
template <class T>
class My_Heap
{
private:T* pRoot; //指向堆的指针,实际上是一个动态数组int len; //元素个数int MaxLen; //容量
public:My_Heap(){pRoot = nullptr;len = MaxLen = 0;}~My_Heap(){delete[] pRoot;pRoot = nullptr;len = MaxLen = 0;}//往堆中插入元素void insert(const T& data);//遍历void travel()const;//删除堆顶T pop();
};
----------- 往堆中插入元素
我们采用 小顶堆的方式,即保证孩子节点要比父亲节点大。
采用动态内存分配的方法,插入一个节点到数组中。
从堆底开始,根据下标关系找到对应的父节点.
插入步骤:(小顶堆)
- 比较插入节点与当前父节点的关系
- 如果比父节点小,则当前节点需要上提,交换当前节点与父节点的值
- 如果比父节点大,则说明不冲突,则直接退出即可,因为经过以前的处理此情况一定是合法的。
- 继续比较,直到不冲突或者到达了根节点为止。
注意:我们使用自底向上的方式,每次比较当前节点与父节点的关系,然后需要将当前节点往上提,继续比较和上一层的关系
图例:
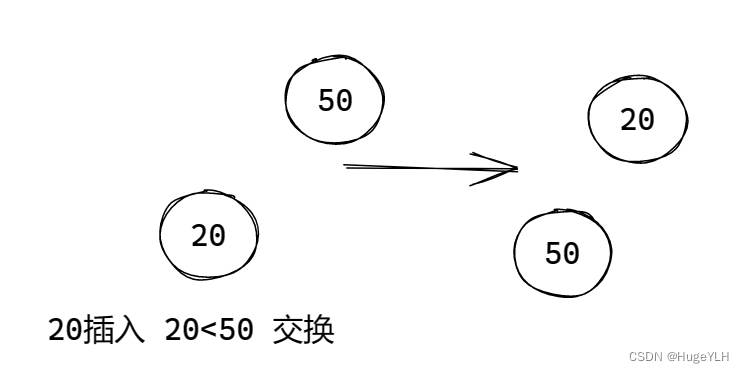
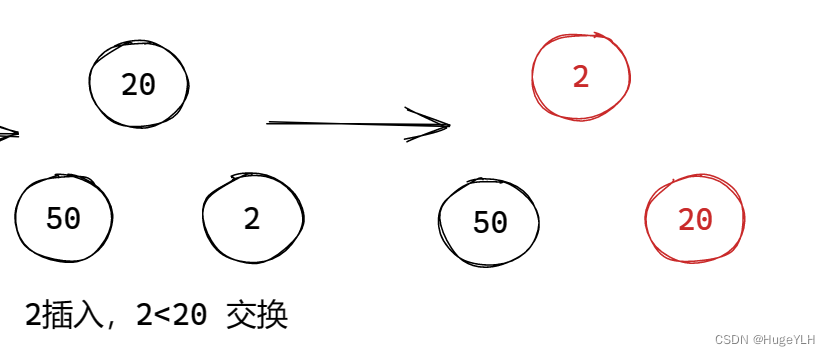
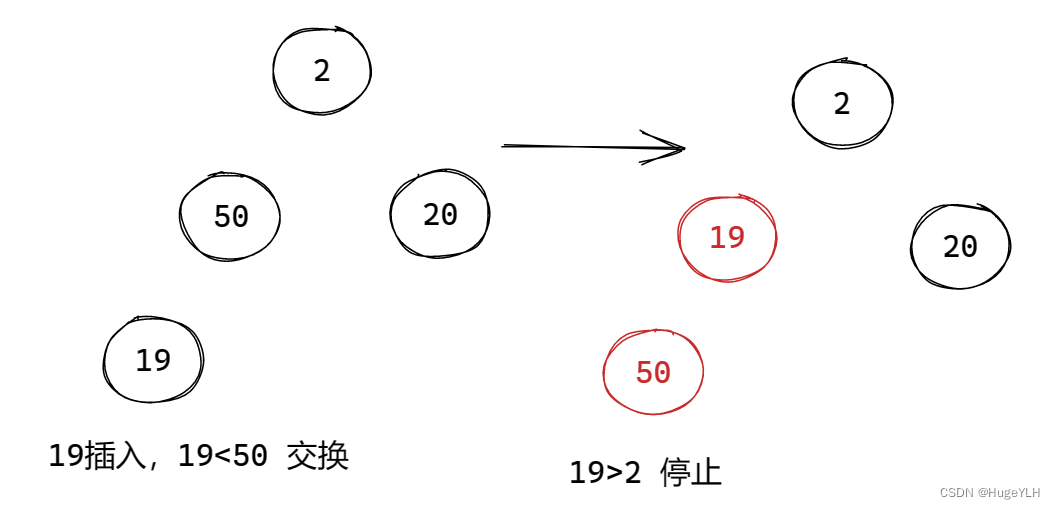
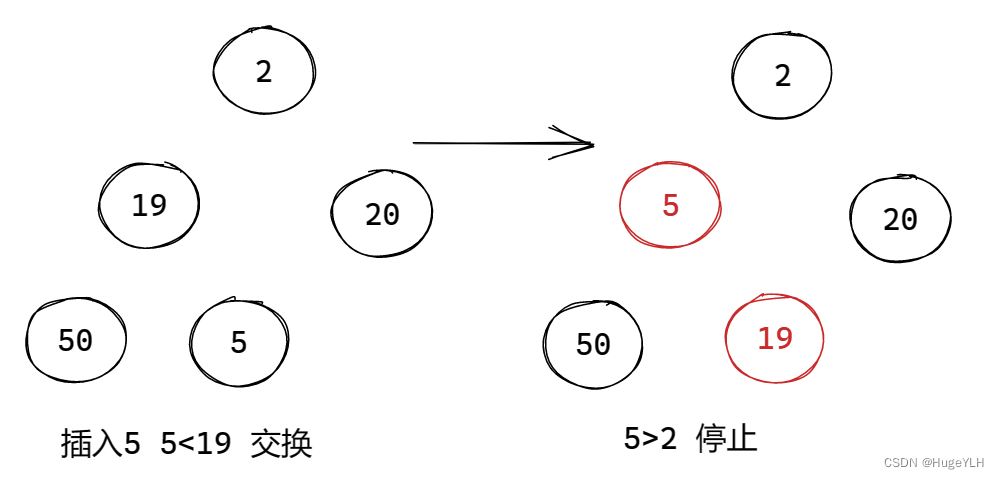
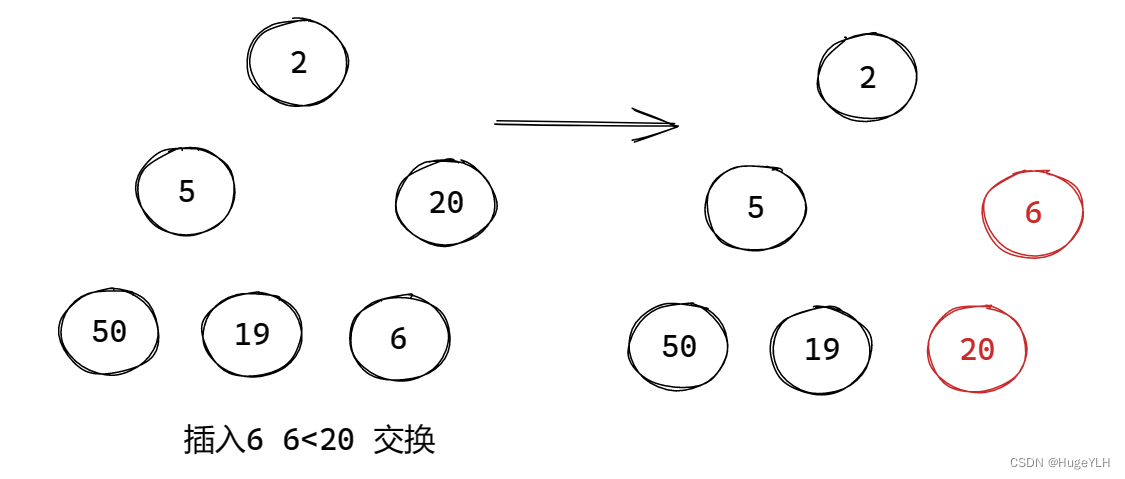
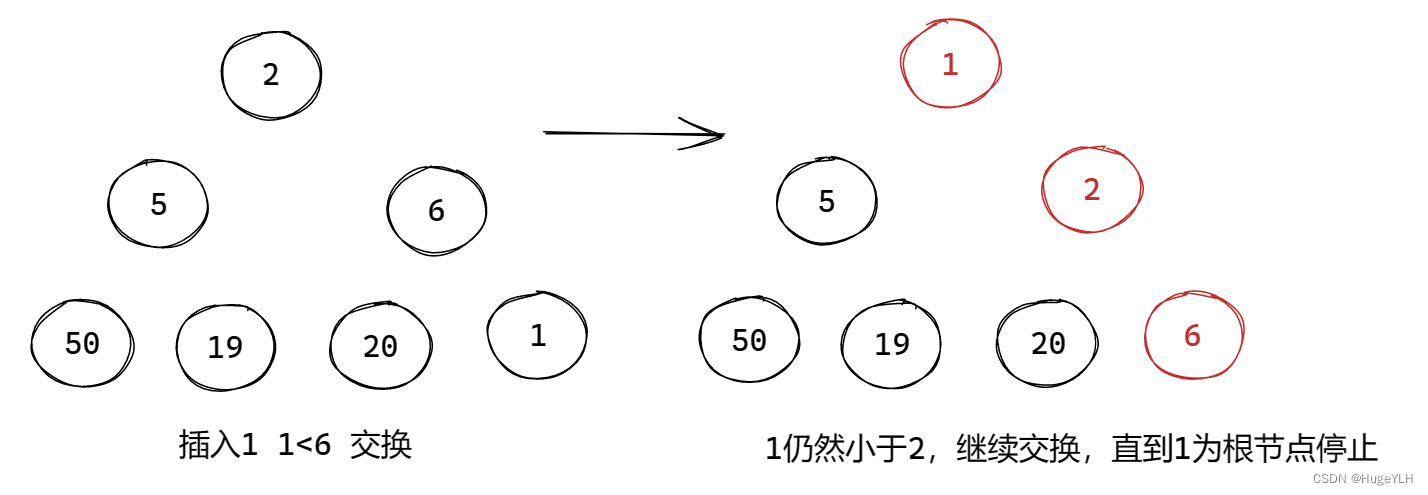
要点:从下往上遍历,交换不合适的节点。
template<class T>
inline void My_Heap<T>::insert(const T& data)
{//动态数组//1 像动态数组一样进来if (MaxLen <= len) {//需要申请//计算需要申请的内存大小 //>>1 右移一位 等同于除以2MaxLen = MaxLen + (((MaxLen >> 1) > 1) ? (MaxLen >> 1) : 1);//1 开内存T* pNew = new T[MaxLen];if (pRoot) {//2 pArr指向内存段中数据拷贝到pNew指向内存段memcpy(pNew, pRoot, sizeof(T) * len);//3 释放pArr指向内存段delete[] pRoot;}//4 pArr指向新开内存pRoot = pNew;}pRoot[len++] = data;//循环和父节点比较,如果冲突交换,不冲突,覆盖if (len == 1){return;}int CurrentIdx= len - 1; //孩子节点int ParentIdx = (CurrentIdx - 1) / 2; //父节点T temp;while (1){if (CurrentIdx <= 0)break; //没有父节点,循环结束ParentIdx = (CurrentIdx - 1) / 2;if (pRoot[ParentIdx] < pRoot[CurrentIdx])break; //不冲突,孩子父亲大,则停止//否则,交换元素temp = pRoot[ParentIdx];pRoot[ParentIdx] = pRoot[CurrentIdx];pRoot[CurrentIdx] = temp;//遍历完一次后,接着往上移动,开始重新一次比较CurrentIdx = ParentIdx;}
}
不使用动态内存分配:
void InsertData(int val){arr[++this->size] = val;if (this->size == 1) return;int curLen = this->size;//当前节点int parentLen = curLen >> 1;//父节点while (true){if (curLen <= 1) break;//到达根节点,退出//比较和父节点的关系,比父节点小则交换parentLen = curLen >> 1;if (arr[curLen] > arr[parentLen]){break;}swap(arr[curLen], arr[parentLen]);curLen = parentLen;}}
----------- 删除堆顶
从堆顶开始,把最后一个元素覆盖堆顶元素,接着根据下标关系,找到堆顶的孩子节点,比较两个孩子谁是最小孩子,如果堆顶比最小孩子节点小,则退出(小顶堆)。否则,交换两个节点,要保证父小于子。然后顶堆往下移动,移动到下一层的父节点,比较父子关系。确保在覆盖了原堆顶(即删除了原堆顶)后,整个堆结构仍然是以小堆顶的结构,因此要进行重排,直到数组下标越界为止。
步骤:
- 最后一个元素覆盖堆顶元素
- 当前节点寻找两个孩子节点的最小的那个,并且把那个最小的与当前节点的值作交换
- 当前节点下移,继续寻找最小的元素并且作交换
- 直到超过了下界之后停止。
注意:如果堆顶元素比左右孩子最小的元素都小,则不冲突,因此直接结束循环
图例:
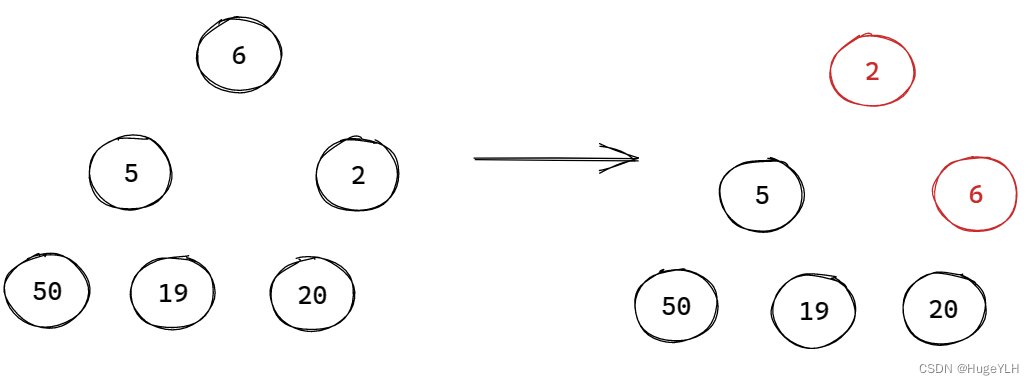
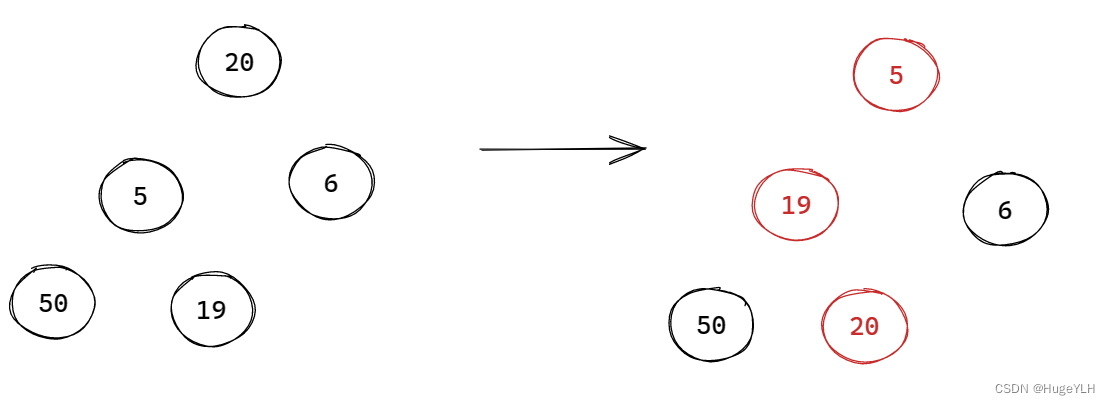
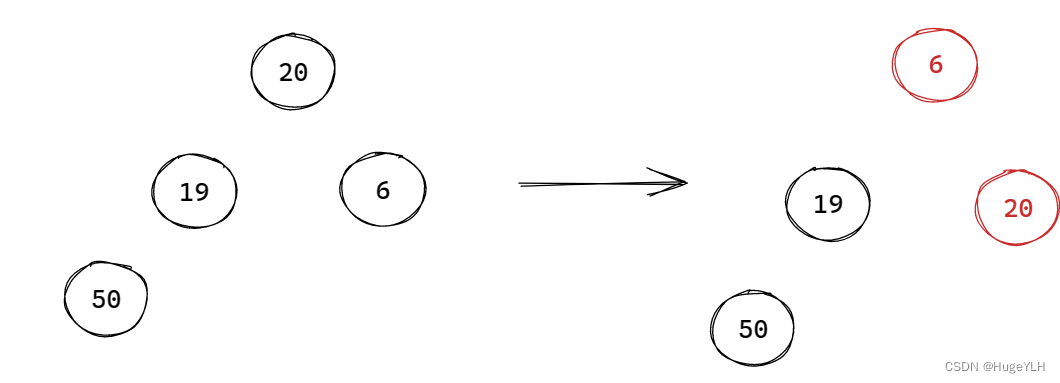
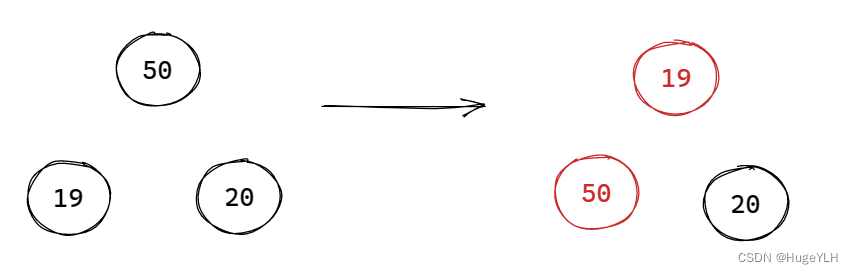
要点:从上往下遍历,重排堆结构的父子关系。
template <class T>
//删除堆顶
T MyHeap<T>::pop(){if (0 == len){cout << "堆为空,删除失败!" << endl;return (T)0;}//没法删if (1 == len){//只有一个len--;return pRoot[0];}//1 临时保存堆顶元素T temp = pRoot[0];//2 最后一个覆盖堆顶元素pRoot[0] = pRoot[len - 1];//3 循环 int currentIdx = 0;//从堆顶开始int minChildIdx;while (1){//数组结束 if ((currentIdx * 2 + 1) > (len - 1) ||(currentIdx * 2 + 2) > (len - 1)){break;}// 找到最小的孩子 minChildIdx = currentIdx * 2 + 1;//假定左孩子比较小//如果左孩子比右孩子大,右孩子最小if (pRoot[minChildIdx] > pRoot[minChildIdx + 1]) minChildIdx++;//比最小孩子还小 循环结束if (pRoot[len-1] < pRoot[minChildIdx]) break;//当前位置和最小孩子交换 //子覆盖父//简单交换方式temp1 = pRoot[CurrentIdx];pRoot[CurrentIdx] = pRoot[MinChildIdx];pRoot[MinChildIdx] = temp1;//往下移动currentIdx = minChildIdx;}//4 返回len--;return temp;
}
不使用动态内存分配
int pop(){/*删除堆顶元素*/if (this->size == 1){this->size = 0;return arr[1];}//1. 最后一个元素覆盖堆顶元素int temp = arr[1];arr[1] = arr[this->size];int curLen = 1;//当前节点int childLen = curLen << 1;//孩子节点while (true){//下移超过了边界则退出if (((curLen << 1) > this->size) || (curLen << 1 | 1) > this->size){break;}//找到两个孩子中最小的一个childLen = curLen << 1;//默认最小的是左孩子if (arr[childLen] > arr[childLen + 1]){childLen += 1;//最小的为右孩子}//堆顶比最小的孩子还小,则无需交换if (arr[this->size] < arr[childLen]) break;//交换当前节点与孩子节点的值swap(arr[childLen], arr[curLen]);curLen = childLen;//下移到孩子}this->size--;//最后总的个数要减一个return temp;}
堆排序构建
template <class T>
//直接用数组方式来构建堆
void MyHeap<T>::initHeap(T* pArr, int size){//开内存maxLen = size;len = 0;pRoot = new T[size];//数据进来pRoot[len++] = pArr[0];//第一个int currentIdx;int parentIdx;for (int i = 1; i < size; i++){currentIdx = len;parentIdx = (currentIdx - 1) / 2;//数据先放进来pRoot[currentIdx] = pArr[i];while (1){if (currentIdx <= 0) break;//没有父节点 循环结束parentIdx = (currentIdx - 1) / 2;if (pRoot[parentIdx] < pRoot[currentIdx]) break;//冲突 父节点覆盖子节点pRoot[currentIdx] = pRoot[parentIdx];//往上移currentIdx = parentIdx;}//新数据覆盖回来pRoot[currentIdx] = pArr[i];//个数增加len++;}
}
完整代码及测试
动态分配版本
#pragma once
#include <iostream>
using namespace std;
template <class T>
class My_Heap
{
private:T* pRoot; //指向堆的指针,实际上是一个动态数组int len; //元素个数int MaxLen; //容量
public:My_Heap(){pRoot = nullptr;len = MaxLen = 0;}~My_Heap(){delete[] pRoot;pRoot = nullptr;len = MaxLen = 0;}//往堆中插入元素void insert(const T& data);//遍历void travel()const;//删除堆顶T pop();void initHeap(T* pArr, int size);
};template<class T>
inline void My_Heap<T>::insert(const T& data)
{//动态数组//1 像动态数组一样进来if (MaxLen <= len) {//需要申请//计算需要申请的内存大小 //>>1 右移一位 等同于除以2MaxLen = MaxLen + (((MaxLen >> 1) > 1) ? (MaxLen >> 1) : 1);//1 开内存T* pNew = new T[MaxLen];if (pRoot) {//2 pArr指向内存段中数据拷贝到pNew指向内存段memcpy(pNew, pRoot, sizeof(T) * len);//3 释放pArr指向内存段delete[] pRoot;}//4 pArr指向新开内存pRoot = pNew;}pRoot[len++] = data;//循环和父节点比较,如果冲突交换,不冲突,覆盖if (len == 1){return;}int CurrentIdx= len - 1; //孩子节点int ParentIdx = (CurrentIdx - 1) / 2; //父节点T temp;while (1){if (CurrentIdx <= 0)break; //没有父节点,循环结束ParentIdx = (CurrentIdx - 1) / 2;if (pRoot[ParentIdx] < pRoot[CurrentIdx])break; //不冲突,循环继续//效率较低temp = pRoot[ParentIdx];pRoot[ParentIdx] = pRoot[CurrentIdx];pRoot[CurrentIdx] = temp;//往上移动CurrentIdx = ParentIdx;}
}template<class T>
inline void My_Heap<T>::travel() const
{for (int i = 0; i < len; i++){cout << pRoot[i] << " ";}cout << endl;
}template<class T>
inline T My_Heap<T>::pop()
{if (len == 0){cout << "堆为空!\n";return (T)0;}if (len == 1){len--; //只有一个元素return pRoot[0];}//1. 临时保存堆顶元素T temp = pRoot[0];T temp1;//2. 最后一个元素覆盖堆顶元素pRoot[0] = pRoot[len - 1];//从堆顶开始int CurrentIdx = 0;int MinChildIdx;while (1){//越界if ((CurrentIdx * 2 + 1) > (len - 1) ||(CurrentIdx * 2 + 2) > (len - 1)){break;}//找到最小孩子//先假设左孩子比较小MinChildIdx = CurrentIdx * 2 + 1;if (pRoot[MinChildIdx] > pRoot[MinChildIdx + 1]){MinChildIdx++; //右孩子比较小}//如果比最小孩子还小if (pRoot[len-1] < pRoot[MinChildIdx])break;//需要交换,采用简单交换, 子覆盖父temp1 = pRoot[CurrentIdx];pRoot[CurrentIdx] = pRoot[MinChildIdx];pRoot[MinChildIdx] = temp1;//父节点往下移动CurrentIdx = MinChildIdx;}len--;return temp;
}template <class T>
//直接用数组方式来构建堆
void My_Heap<T>::initHeap(T* pArr, int size) {//开内存MaxLen = size;len = 0;pRoot = new T[size];//数据进来pRoot[len++] = pArr[0];//第一个int currentIdx;int parentIdx;for (int i = 1; i < size; i++) {currentIdx = len;parentIdx = (currentIdx - 1) / 2;//数据先放进来pRoot[currentIdx] = pArr[i];while (1) {if (currentIdx <= 0) break;//没有父节点 循环结束parentIdx = (currentIdx - 1) / 2;if (pRoot[parentIdx] < pRoot[currentIdx]) break;//冲突 父节点覆盖子节点pRoot[currentIdx] = pRoot[parentIdx];//往上移currentIdx = parentIdx;}//新数据覆盖回来pRoot[currentIdx] = pArr[i];//个数增加len++;}
}
#include "MyHeap.h"#define NUM 11
int main()
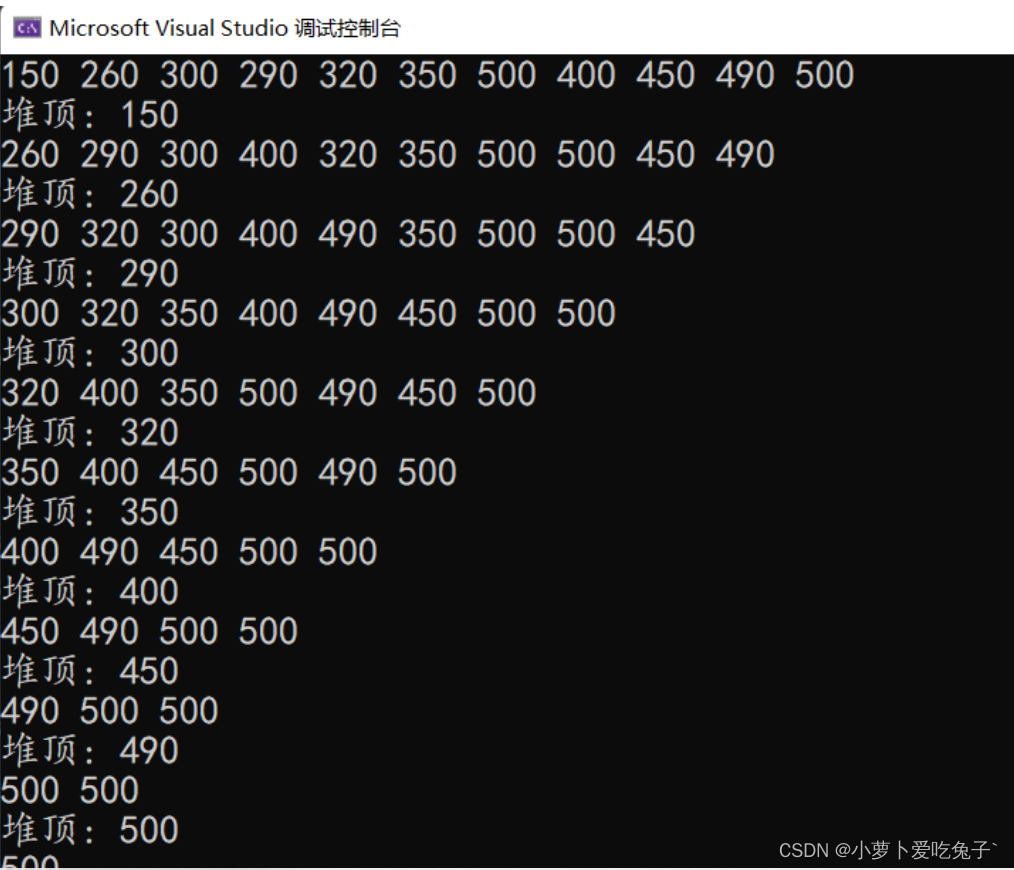
{int arr[NUM] = { 150,260,300,290,320,350,500,400,450,490,500 };My_Heap<int> a;/*for (int i = 0; i < NUM; i++){a.insert(arr[i]);a.travel();}*/a.initHeap(arr, NUM);a.travel();return 0;
}非动态版本
P1177 【模板】快速排序 ----排序测试
Ac code
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
using namespace std;
#define int long long
const int N = 1e5 + 10;
const int CurSize = 1e5 + 10;
struct Tree
{int arr[N];int size;Tree() { memset(arr, 0, sizeof(arr)); size = 0; }void InsertData(int val){arr[++this->size] = val;if (this->size == 1) return;int curLen = this->size;//当前节点int parentLen = curLen >> 1;//父节点while (true){if (curLen <= 1) break;//到达根节点,退出//比较和父节点的关系,比父节点小则交换parentLen = curLen >> 1;if (arr[curLen] > arr[parentLen]){break;}swap(arr[curLen], arr[parentLen]);curLen = parentLen;}}int pop(){/*删除堆顶元素*/if (this->size == 1){this->size = 0;return arr[1];}//1. 最后一个元素覆盖堆顶元素int temp = arr[1];arr[1] = arr[this->size];int curLen = 1;//当前节点int childLen = curLen << 1;//孩子节点while (true){//下移超过了边界则退出if (((curLen << 1) > this->size) || (curLen << 1 | 1) > this->size){break;}//找到两个孩子中最小的一个childLen = curLen << 1;//默认最小的是左孩子if (arr[childLen] > arr[childLen + 1]){childLen += 1;//最小的为右孩子}//堆顶比最小的孩子还小,则无需交换if (arr[this->size] < arr[childLen]) break;//交换当前节点与孩子节点的值swap(arr[childLen], arr[curLen]);curLen = childLen;//下移到孩子}this->size--;//最后总的个数要减一个return temp;}
};
signed main()
{Tree t;int n;cin >> n;for (int i = 1; i <= n; i++){int p;cin >> p;t.InsertData(p);}while (t.size != 0){cout << t.pop() << " ";}return 0;
}
相关文章:

数据结构_ 堆结构与堆排序(c++ 实现 + 完整代码 )
堆结构与堆排序 文章目录堆结构与堆排序引入堆堆结构所满足的数学特性准备代码----------- 往堆中插入元素----------- 删除堆顶堆排序构建完整代码及测试动态分配版本非动态版本引入堆 二叉树 具有左孩子与右孩子的最普通的二叉树。 满二叉树 特殊的二叉树:每个节…...
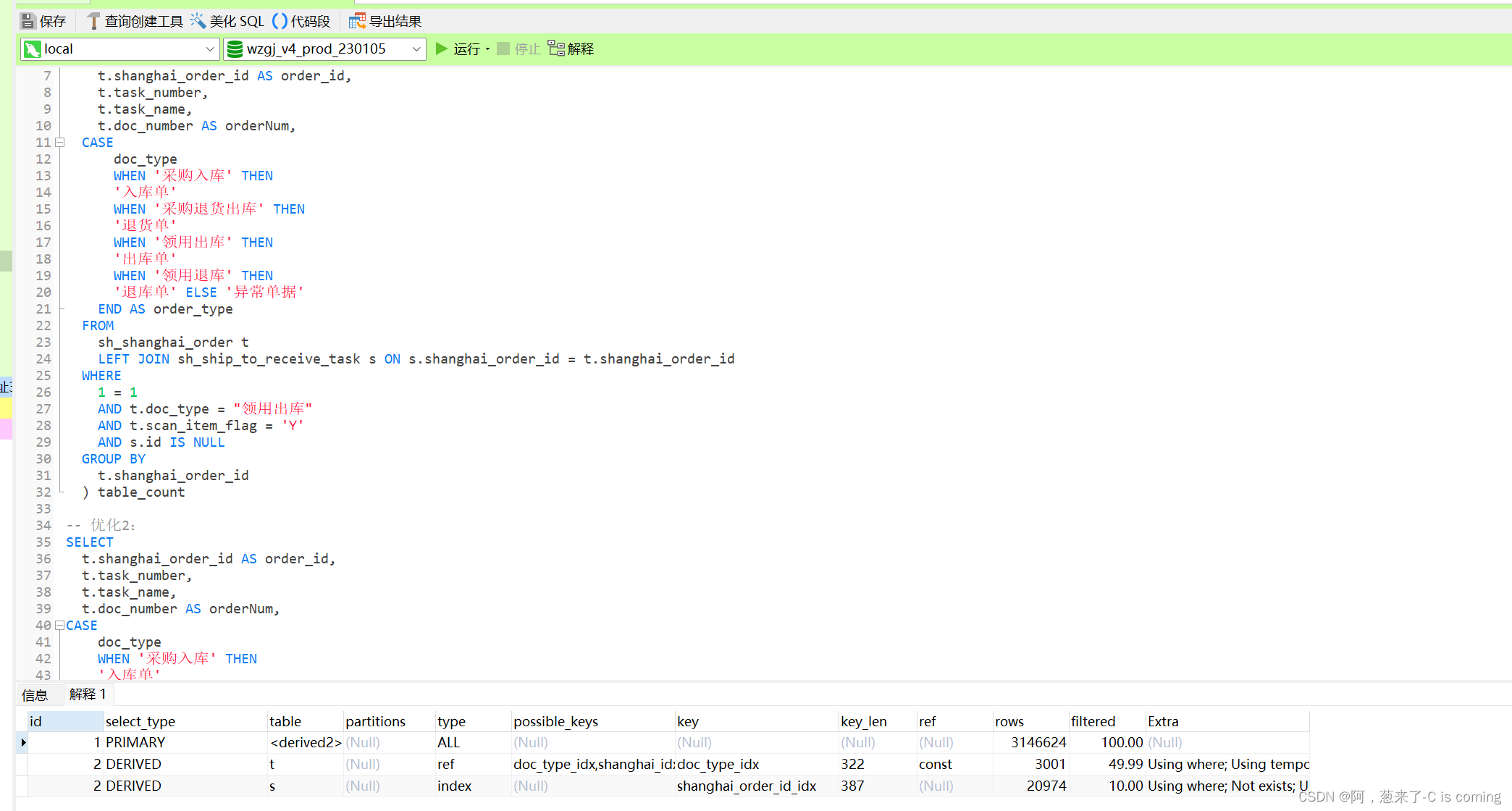
【MySQL】sql中explain解释和应用
这里写目录标题学习原因MySQL中explain的使用和用法解释explain的使用explain 运行结果的意义文字展示表格展示参考资料:结束语学习原因 在对sql的优化过程中使用了explain对指定的sql进行查看它的运行效果,以便找出sql的性能特点并进行优化 MySQL中ex…...
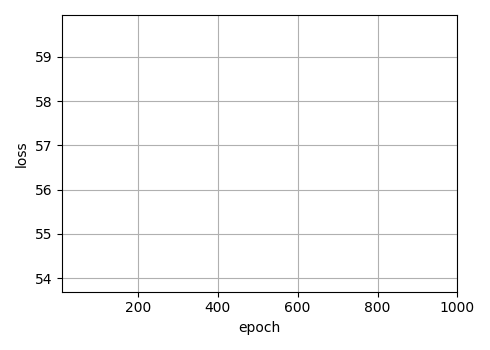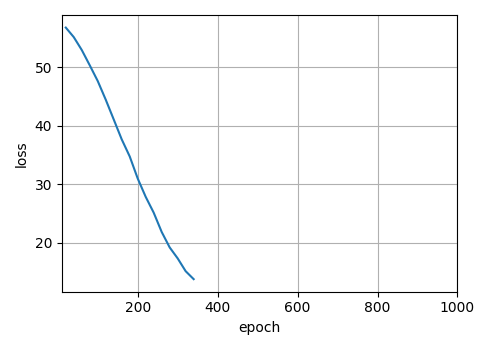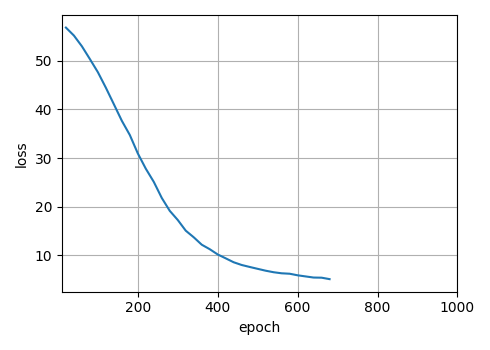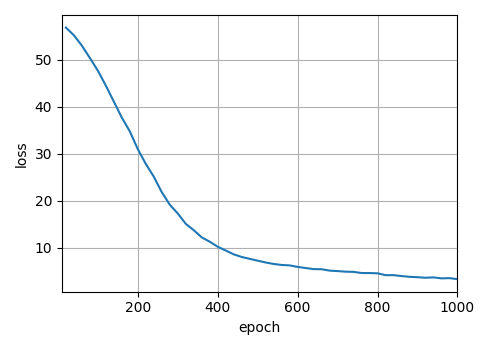
从零实现深度学习框架:Seq2Seq从理论到实战【实战篇】
来源:投稿 作者:175 编辑:学姐 往期内容: 从零实现深度学习框架1:RNN从理论到实战(理论篇) 从零实现深度学习框架2:RNN从理论到实战(实战篇) 从零实现深度…...

【数据结构入门】-链表之单链表(1)
个人主页:平行线也会相交 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【数据结构初阶(C实现)】 文章标题回顾链表链表的概念及结构各种节点打印链表尾插创建节点尾删头插头删查找在pos…...
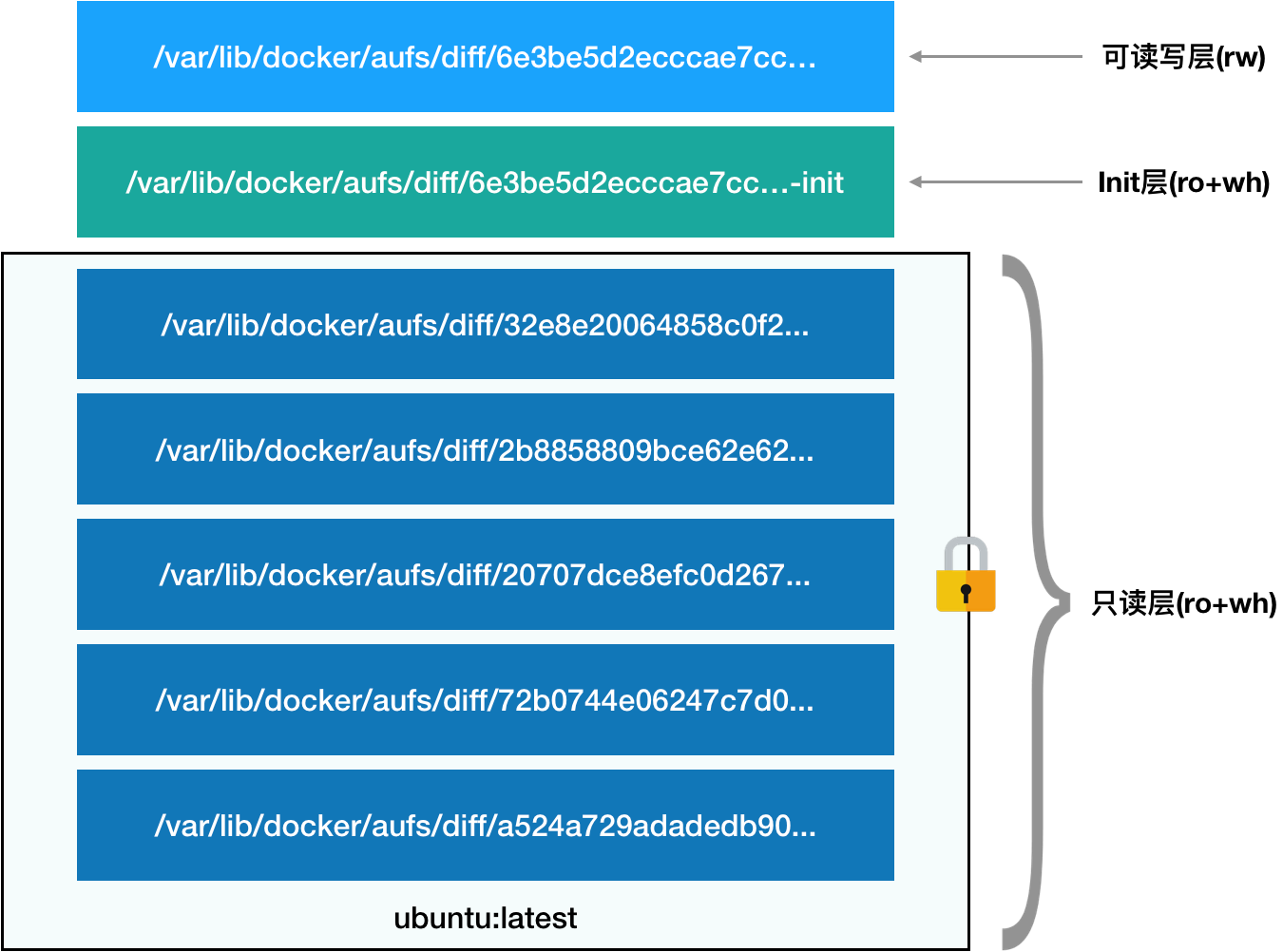
Docker竟如此简单!
文章目录什么是容器?容器隔离何为“边界”?容器和虚拟机一样吗?基于 Linux Namespace 隔离机制的弊端容器限制何为“限制”?Cgroups 对资源的限制能力缺陷单进程模型容器镜像容器的诞生容器的一致性何为“层(layer&…...
在外包干了几年,感觉自己都快费了
先说一下自己的情况。大专生,18年通过校招进入湖南某软件公司,干了接近2年的点点点,今年年上旬,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了五年的功能测试…...
Java实现多线程有几种方式(满分回答)
目录JDK8 创建的线程的两种方式orcle文档解释方式一:继承Thread类方式二:实现Runnable接口同时用两种的情况其他间接创建方式Callable接口线程池JDK8 创建的线程的两种方式 orcle文档解释 orcle文档:https://docs.oracle.com/javase/8/docs…...

实例4:树莓派GPIO控制舵机转动
实例4:树莓派GPIO控制舵机转动 实验目的 通过背景知识学习,了解舵机的外观及基本运动方式。了解四足机器人mini pupper腿部单个舵机的组成结构。通过GPIO对舵机进行转动控制,熟悉PWM。了解mini pupper舵机组的整体调零。 实验要求 使用Py…...

【音视频处理】为什么MP3不是无损音乐?音频参数详解,码率、采样率、音频帧、位深度、声道、编码格式的关系
大家好,欢迎来到停止重构的频道。上期我们讨论了视频的相关概念,本期我们讨论音频的相关概念。包括采样率、码率、单双声道、音频帧、编码格式等概念。这里先抛出一个关于无损音频的问题。为什么48KHz采样率的.mp3不是无损音乐 ,而48KHz采样率…...

Linux 环境变量
Linux 环境变量能帮你提升 Linux shell 体验。很多程序和脚本都通过环境变量来获取系统信息、存储临时数据和配置信息。在 Linux 系统上有很多地方可以设置环境变量,了解去哪里设置相应的环境变量很重要。 认识环境变量 bash shell 用环境变量(environme…...

从功能测试(点点点)到进阶自动化测试,实现薪资翻倍我只用了3个月时间
前言 从事测试工作已3年有余了,今天想聊一下自己刚入门时和现在的今昔对比,虽然现在也没什么成就,只能说笑谈一下自己的测试生涯,各位看官就当是茶余饭后的吐槽吧,另外也想写一写自己的职场感想,希望对刚开…...

aspnetcore 原生 DI 实现基于 key 的服务获取
你可能想通过一个字符串或者其他的类型来获取一个具体的服务实现,那么在 aspnetcore 原生的 MSDI 中,如何实现呢?本文将介绍如何通过自定义工厂来实现。我们现在恰好有基于 Json 和 MessagePack 的两种序列化器有一个接口是这样的publicinter…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 -最大子矩阵和(Python) | 机试题+算法思路+考点+代码解析 【2023】
最大子矩阵和 题目 给定一个二维整数矩阵 要在这个矩阵中 选出一个子矩阵 使得这个子矩阵内所有的数字和尽量大 我们把这个子矩阵成为“和最大子矩阵” 子矩阵的选取原则,是原矩阵中一段相互连续的矩形区域 输入 输入的第一行包含两个整数N,M (1 <= N,M <= 10) 表示…...
)
C2驾照科一学习资料(1)
目录 记1分 记3分 记6分 记9分 记12分 你有不伤别人的教养 却缺少一种不被人伤的气场 若没人护你周全 就请善良中带点锋芒为自己保驾护航 这个世界你若好到毫无保留 对方就会坏到肆无忌惮 记1分 《道路交通安全违法行为记分管理办法》规定,机动车驾驶人有下列…...

4576: 移动数组元素
描述给定一个n个元素的一维数组,将下标从0到p的元素全部平移到数组尾部。输入第一行有两个正整数n和p(2<n<100,0<p<n)。第二行有n个整数,表示数组的各个元素。输出在一行中按顺序输出移动后的各个数组元素…...

字符串中<br>处理
需求: 后端返回的字符串中带有br换行符,前端需要处理行内及行尾的换行符。具体需求可分为以下两个: 若是字符串末尾有换行符,需要去掉。若是字符串内有换行符,有两种需求:①将换行符转换成逗号或其它符号&…...

大数据技术原理与应用介绍
大数据技术原理与应用 概述 大数据不仅仅是数据的“大量化”,而是包含“快速化”、“多样化”和“价值化”等多重属性。 两大核心技术:分布式存储和分布式处理 大数据计算模式 批处理计算流计算图计算查询分析计算 大数据具有数据量大、数据类型繁…...

【Python】序列与列表(列表元素的增删改查,求之,列表推导式、列表的拷贝)
一、序列序列的概念:按照某种顺序排列的数据类型就叫做序列,比如字符串,列表,元组,集合序列的共同点是都有下标,支持index()方法和count(),也支持切片处理(等同于字符串序列的切片处理)l1 [0, …...

update导致死锁
update delete 操作,如果走的索引,对索引和主键索引加行锁 如果没有走索引,锁整张表。 不开启事务,mysql本身也会加锁 一般MYSQL在执行CREATE,ALTER,INSERT等命令时会自动加锁 在对数据进行更新操作时 如果update没用到索引&…...
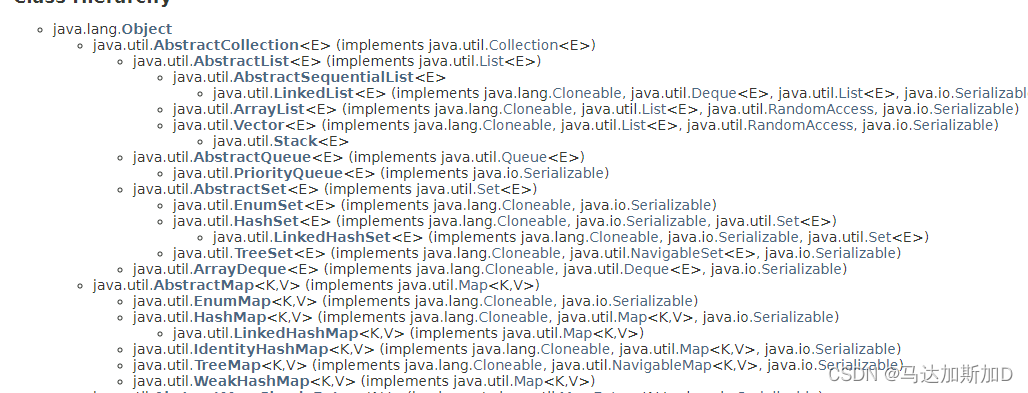
Java 集合 --- 如何遍历Map
Java 集合 --- 如何遍历MapMap的基本操作如何遍历MapType of HashMapMap没有继承Collection接口AbstractMap和AbstractCollection是平级关系 Map的基本操作 package map; import java.util.*; /*** This program demonstrates the use of a map with key type String and val…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
