【数据结构】AVL树的插入与验证
文章目录
- 一、基本概念
- 1.发展背景
- 2.性质
- 二、实现原理
- ①插入操作
- 1.平衡因子
- 1.1平衡因子的更新
- 1.1.1树的高度变化
- 1.1.2树的高度不变
- 2. 旋转
- 2.1左旋
- 2.2右旋
- 2.3右左双旋
- 2.4 左右双旋
- ②验证
- 1.求二叉树高度
- 2. 判断是否为AVL树
- 源码
- 总结
一、基本概念
1.发展背景
-
普通的二叉搜索树在极端情况下会退化成类似链表的形状,从而使查找的效率降低至O(N)。
-
在此基础上,苏联与以色列数学家
Adelson-Velskii 与 苏联数学家Landis,发明出了 AVL树或者说平衡二叉搜索树。


注:第一张——Adelson-Velskii(1922-2014) ,第二张——Landis(1921——1997)
2.性质
- 左右子树的高度差的绝对值不大于1
- 每个子树都是AVL树。
说明:这样做的目的就是为了严格控制平衡,以便于提高查找效率,但是控制高度差一直为0是不可能的,至于为什么不能控制成0,假设只有两个结点必然存在1的高度差。
二、实现原理
①插入操作
1.平衡因子
英文名:balance factor
- 目的:
保证左右子树的高度差的绝对值不大于1 - 大多数的实现方式:
存放的是右子树与左子树的高度差
1.1平衡因子的更新
1.1.1树的高度变化
① 左边新增结点
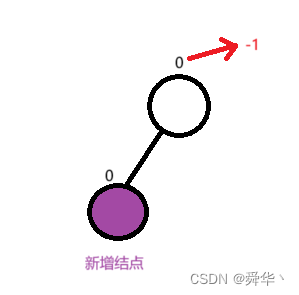
② 右边新增结点
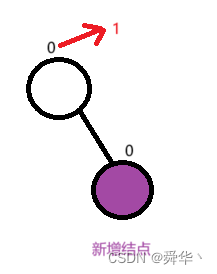
- 总结
- 左边新增,根节点的平衡因子减1
- 右边新增,根节点的平衡因子加1
- 平衡因子从0变为1或者-1
继续分析:
两种情况树的高度增加1,也就是平衡因子从0变为1或者-1,既然高度变化了,可能会导致上面的树不平衡。
如:

此时我们需要向上更新平衡因子,再根据右边高度变化与左边高度变化,决定根的平衡因子加1还是减1。
- 推论:
由于可能会向上更新平衡因子,那么AVL树是三叉链的结构。
如图:
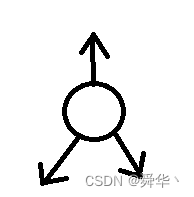
1.1.2树的高度不变
① 左边新增结点
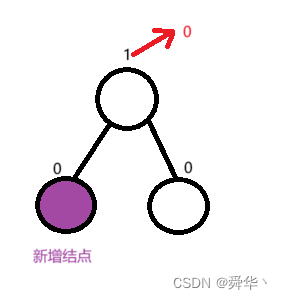
② 右边新增结点
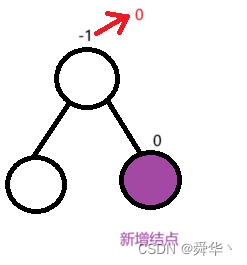
- 同理
- 左边新增,根节点的平衡因子减1
- 右边新增,根节点的平衡因子加1
- 平衡因子由1或者-1变为0
继续分析,这里的根节点的所在树的高度即——左右子树高度的最大值 + 1(根节点的高度)
左右子树的高度的最大值不变,即这颗树高度不变,即不用往上继续更新且达到平衡。
2. 旋转
-
说明:旋转就是让
不平衡的树再次平衡的手段。 -
条件:平衡因子为2或者-2,即高度差的绝对值为2。
-
补充:若平衡因子大于等于3,说明当前树就不是AVL树,需要检验之前的代码。
但是我们又得对情况进行分类讨论,因为不同情况让树再次平衡的旋转方式不同。
2.1左旋
- 说明:也就是右边高度高,需要旋转来降低右边的高度,进而达到平衡。
一步一步分析,先来个最简单的:

此时,旋转过后平衡因子全变为0,且当前树达到平衡。注意此时3结点的左结点为空!(细节)
再举一个例子:
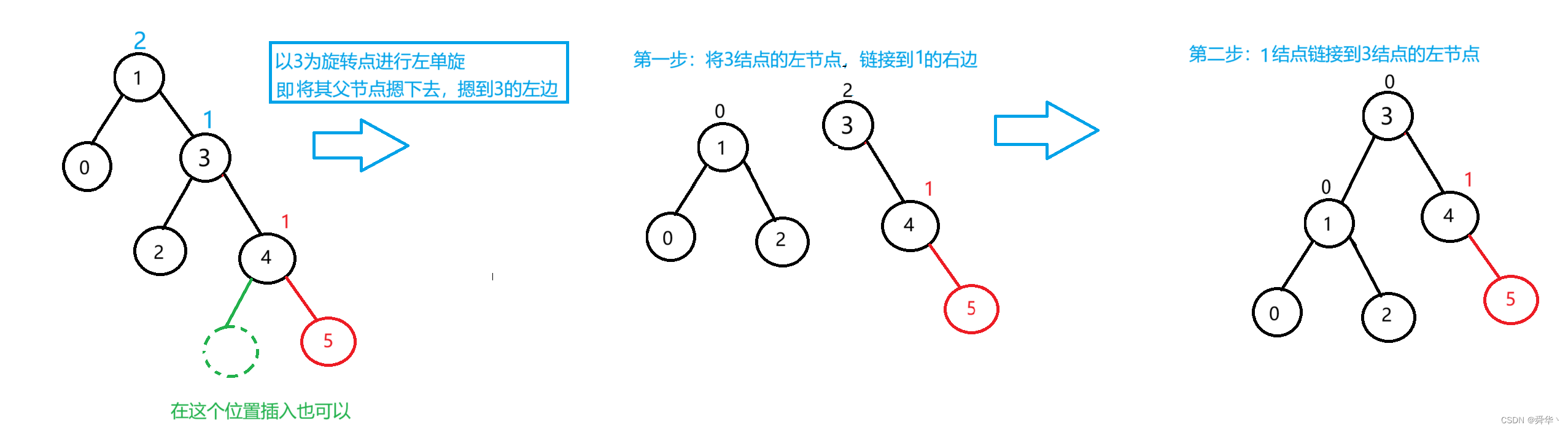
此时,旋转过后平衡因子1和3的平衡因子变为0,且当前树达到平衡,此时我们是不用管其它子树的,因为子树必然是AVL树,要不然更不到根节点就停止了。
最后来一个稍微复杂的例子:
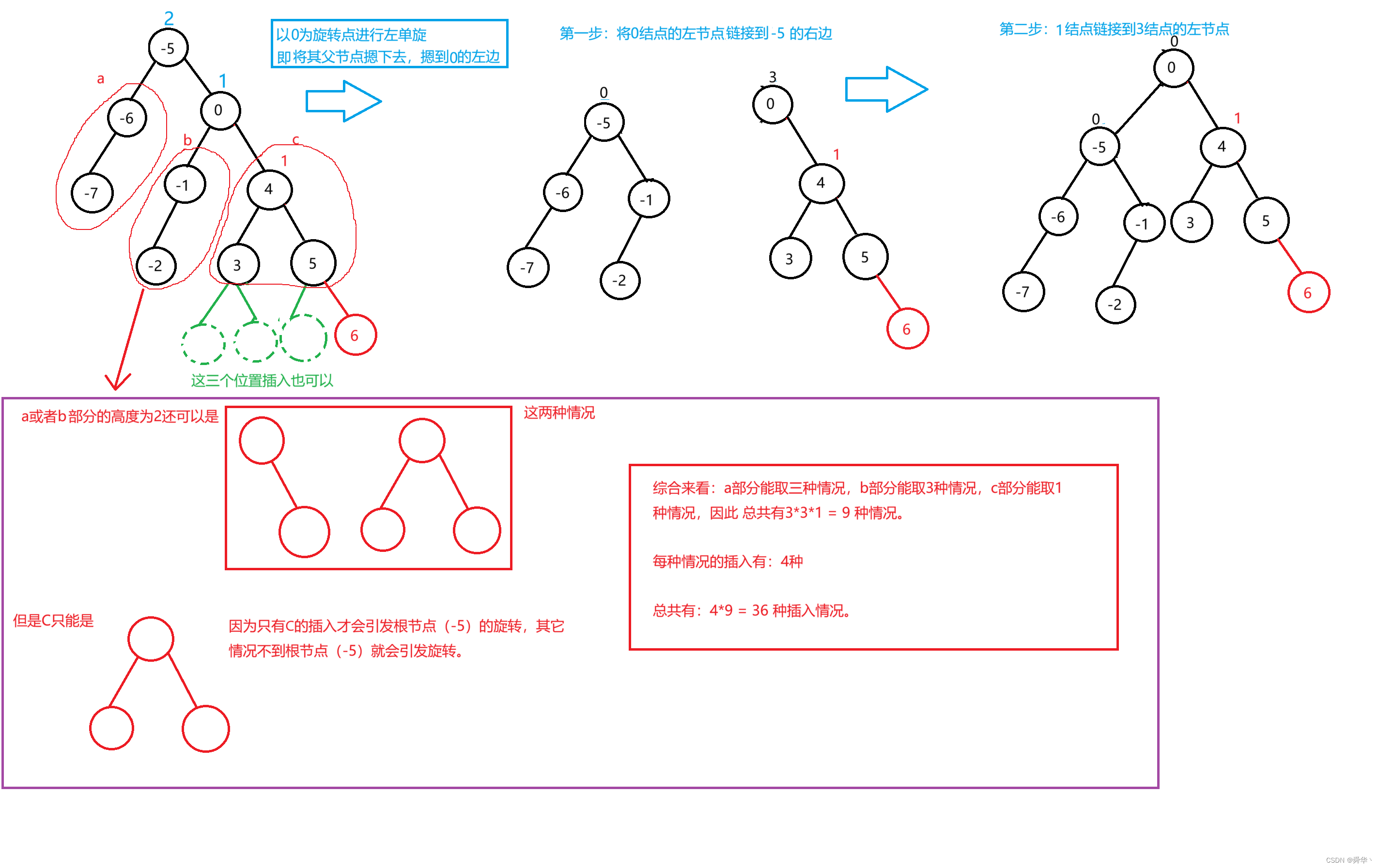
此时,旋转过后平衡因子-5和0的平衡因子变为0,且当前树达到平衡。
这是具体的图便于辅助理解,然后我们再画出所有情况的抽象图:
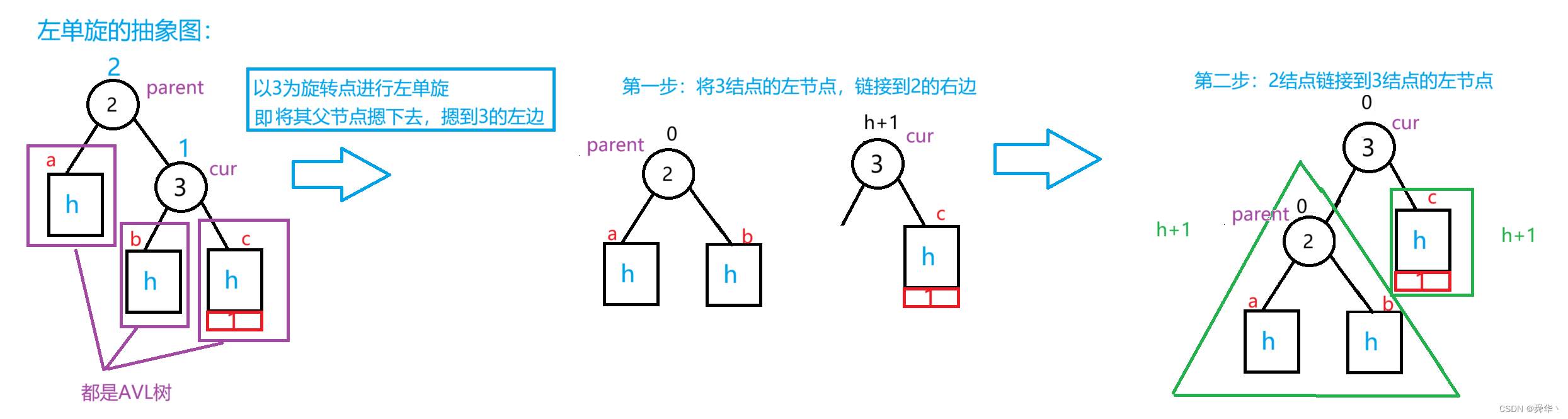
- 总结
只能在c部分上插入结点才可能会引发根节点左单旋,也就是说parent的右边为cur且新增结点在cur的右边。- 旋转过后
cur与parent的平衡因子变为0。
- 细节
- b的父节点连接parent时,需要判断b部分是否为空。
- parent的父节点连接cur时,需要保存一下parent的父节点。
- 根据parent的父节点判断是否需要修改根节点,若为空则修改,若不为空,则将cur链接到parent的父节点,同时更新parent父节点的指向。
- 实现代码
void RotateL(Node* parent){//画图分析://操作的结点有cur,cur_left,ppnodeNode* cur = parent->_right;Node* cur_left = cur->_left;//将parent的右节点改为cur_leftparent->_right = cur_left;//改变cur_left父节点的转向//cur_left可能为空if (cur_left != nullptr){cur_left->_parent = parent;}//将parent链接在cur的左边//为了更新cur的parent需要保存parent的父节点Node* ppnode = parent->_parent;cur->_left = parent;parent->_parent = cur;//ppnode可能为空if (ppnode == nullptr){//需要修改根节点_root = cur;cur->_parent = nullptr;}else{//改变ppnode的指向if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}//更新平衡因子cur->_bf = parent->_bf = 0;}
2.2右旋
说明:也就是左边高度高,需要旋转来降低右边的高度,进而达到平衡。
跟左旋的分析方式一样。
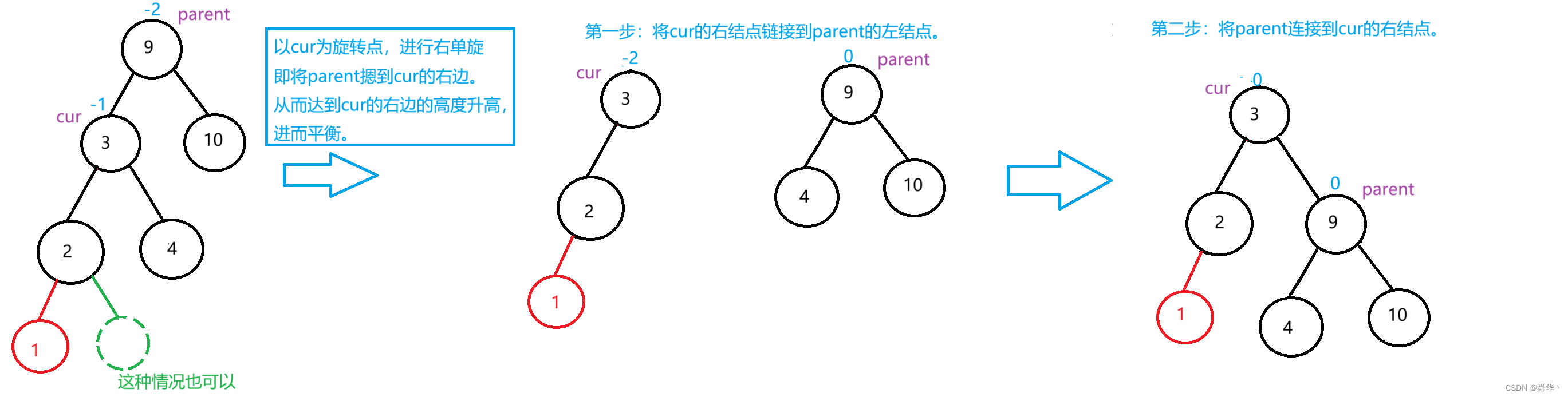
先来个简单的感受一下:

此时,旋转过后平衡因子parent和cur的平衡因子变为0,且当前树达到平衡。
再举一个例子:
最后来一个稍微复杂的例子:
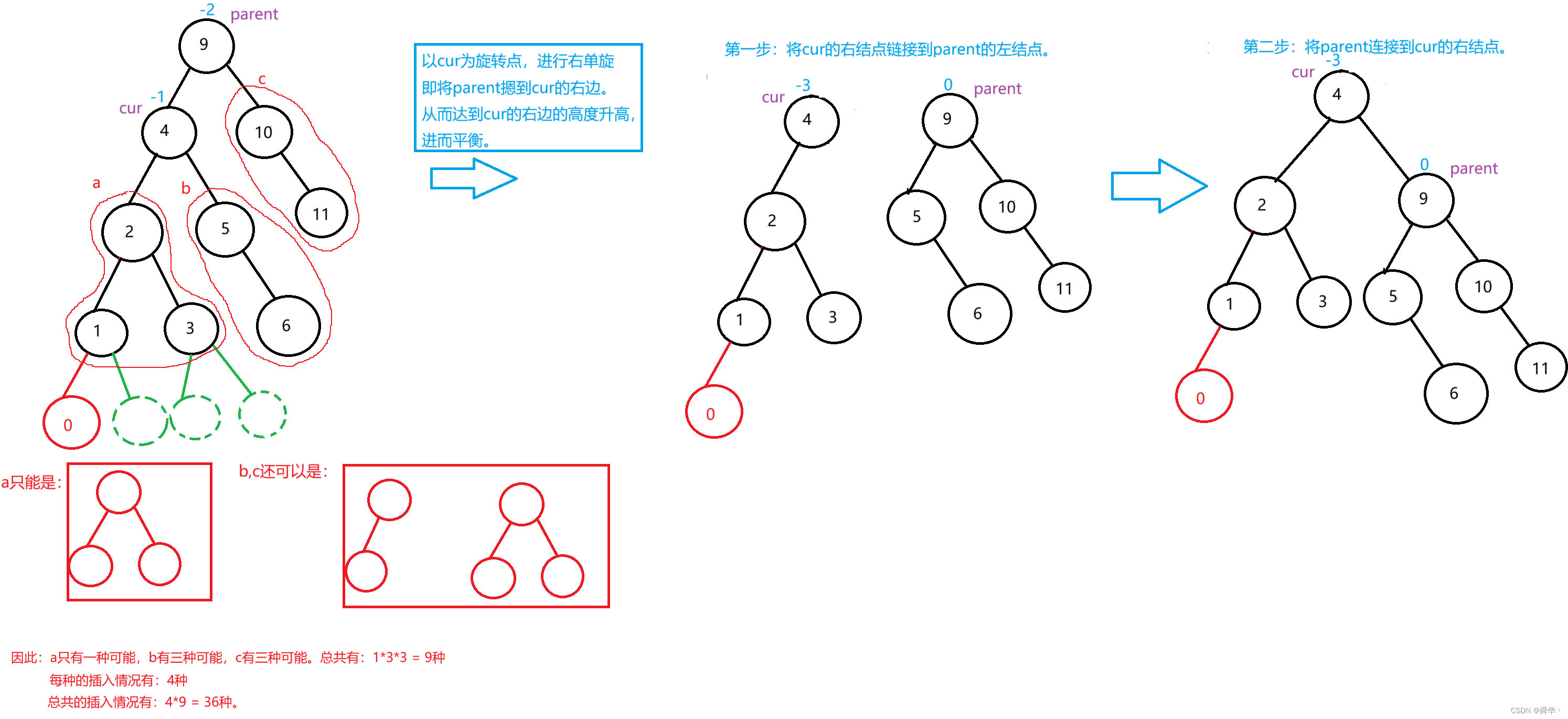
画出所有情况的抽象图:
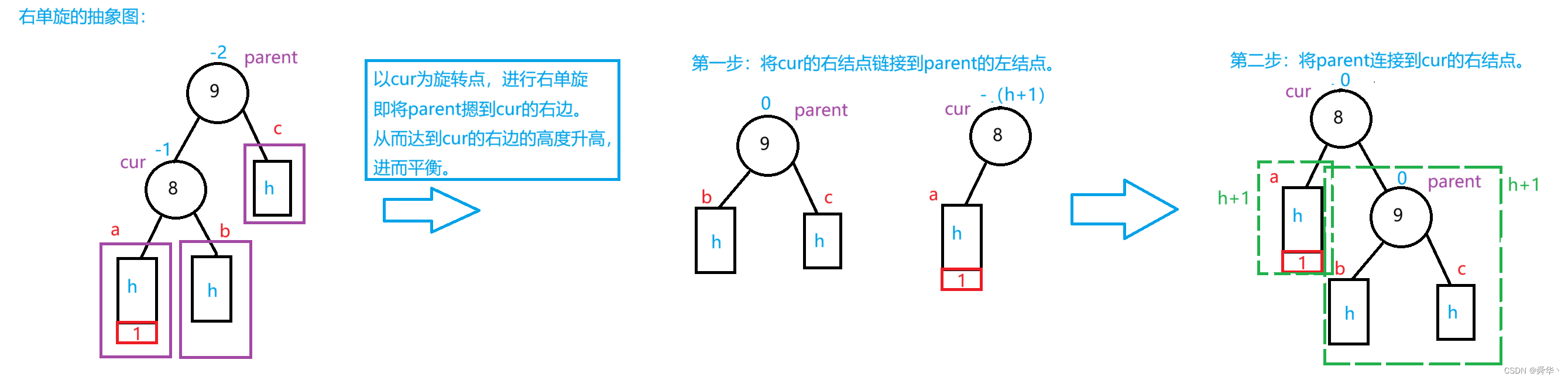
- 总结
只能在a部分上插入结点才可能会引发根节点右单旋,也就是说parent与cur与高度变化的c树的根节点在同一个方向且在parent的左- 旋转过后
cur与parent的平衡因子变为0。
- 细节——同左旋
- b的父节点连接parent时,需要判断b部分是否为空。
- parent的父节点连接cur时,需要保存一下parent的父节点。
- 根据parent的父节点判断是否需要修改根节点,若为空则修改,若不为空,则将cur链接到parent的父节点,同时更新parent父节点的指向。
- 实现代码:
void RotateR(Node* parent){//操作的结点Node* cur = parent->_left;Node* cur_right = cur->_right;//第一步:将cur_right链接到parent的leftparent->_left = cur_right;//更改cur_right的父节点//注意:cur_right可能为空if (cur_right != nullptr){cur_right->_parent = parent;}//第二步:将parent链接到cur的右结点。//先保存一下parent的父节点Node* ppnode = parent->_parent;cur->_right = parent;parent->_parent = cur;//ppnode为空说明需要修改根节点if (ppnode == nullptr){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}//更新平衡因子cur->_bf = parent->_bf = 0;}
2.3右左双旋
- 可以简单理解为,需要进行处理的左旋。
说明:单旋无法解决问题,原因是发生了拐弯,需要用右旋讲折线变为直线,再进行左旋。
因为情况有点多我们就来个简单的,直接化抽象图,看结论比较容易理解。
先来个简单的:
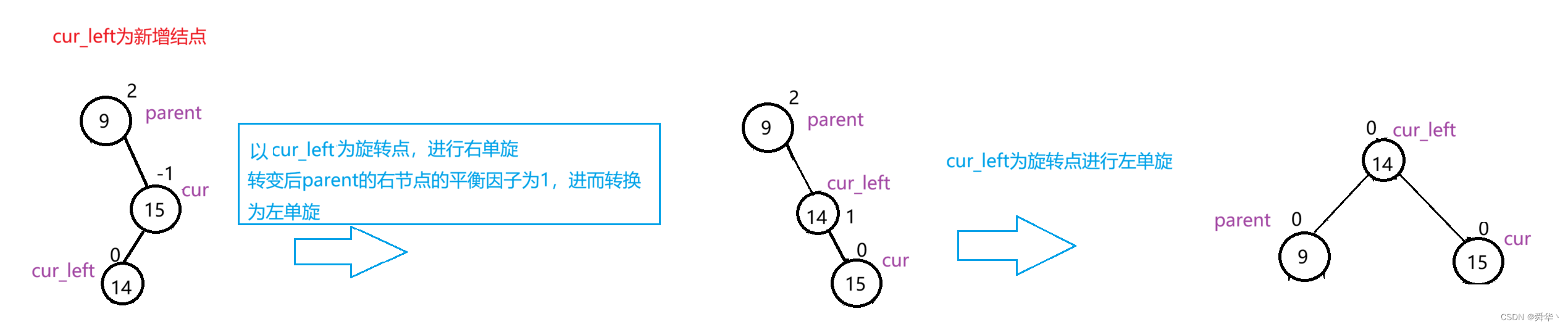
先右旋之后折线变成了直线,变成了左旋的形状,再进行左旋,最后的cur与cur_left与parent的平衡因子变成了0,最终cur_left变成了根节点。
再化抽象图:
初始状态
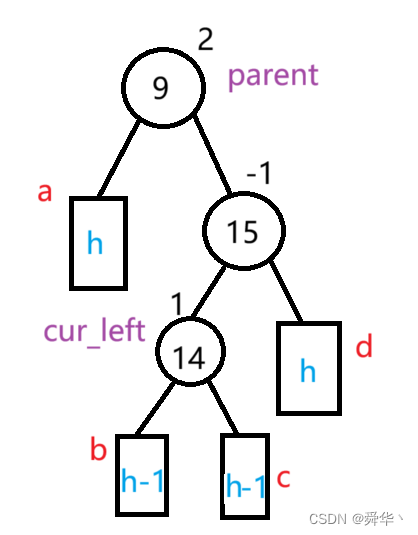
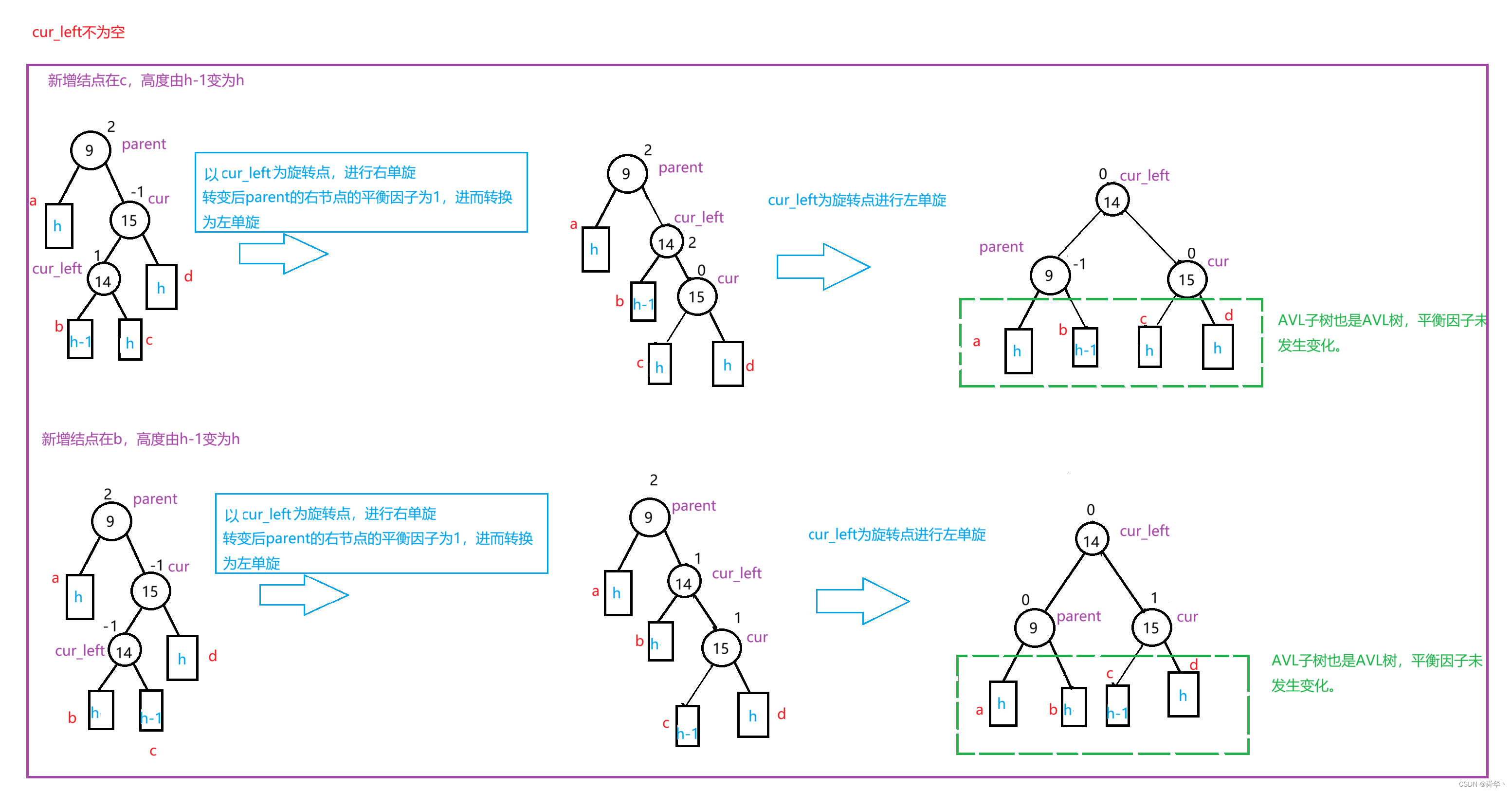
还是一样,不过得分两种情况进行讨论:
- 新增结点在c树上,会导致parent的平衡因子变为-1,cur的平衡因子变为0。
- 新增结点在b树上,会导致parent的平衡因子变为0,cur的平衡因子变为1
- 不管新增结点在谁上,cur_left的平衡因子都为0。
-
看图分析,其实不看新增结点在谁身上,两种最终的旋转的结果是一样的,那我们其实只需先不看新增结点再画图,根据最终的结果再把新增结点添上,其实会更加直观。
-
总结
- 新增结点在c树上,会导致parent的平衡因子变为-1,cur的平衡因子变为0。
- 新增结点在b树上,会导致parent的平衡因子变为0,cur的平衡因子变为1。
- cur_left为新增结点,parent与cur的结点全为0。
- 实现代码:
void RotateRL(Node* parent){Node* cur = parent->_right;Node* cur_left = cur->_left;//CL——CurLeftint CL_bf = cur_left->_bf;RotateR(cur);RotateL(parent);//更新平衡因子if (CL_bf == 0){cur->_bf = parent->_bf = cur_left->_bf = 0;//虽然没必要,但是起到了解耦的作用。}else if (CL_bf == 1){parent->_bf = -1;cur->_bf = cur_left->_bf = 0;}else if(CL_bf == -1){cur->_bf = 1;parent->_bf = cur_left->_bf = 0;}else{cout << __LINE__ << ":" << endl;perror("平衡因子有误");exit(-1);}}
2.4 左右双旋
- 可以理解为,需要进行处理的右旋。
说明:单旋无法解决问题,原因是发生了拐弯,需要用左旋讲折线变为直线,再进行右旋。
分析方法跟右左双旋一样。
先来个简单的:
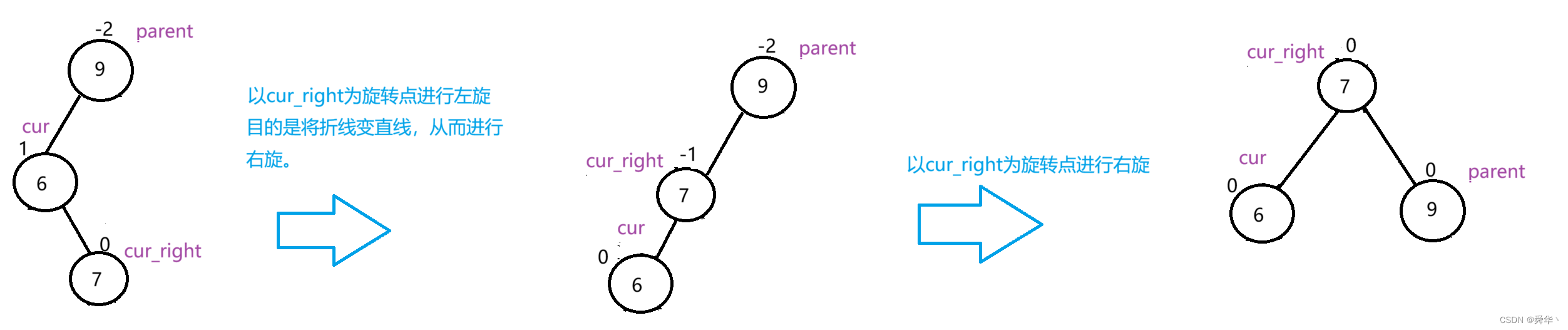
先左旋之后折线变成了直线,变成了右旋的形状,再进行右旋,最后的cur与cur_left与parent的平衡因子变成了0,最终cur_left变成了根节点。
再来个抽象的:
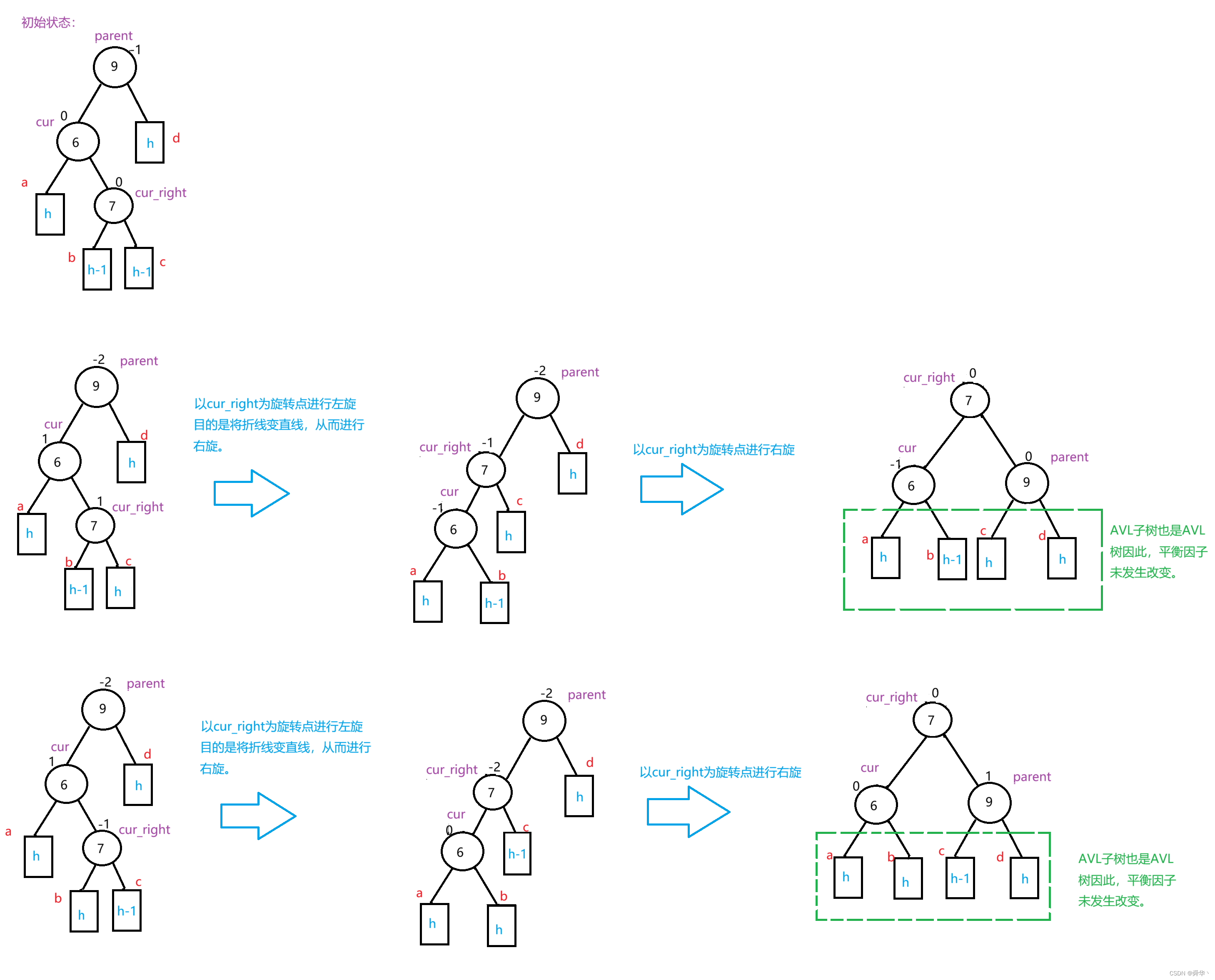
还是一样,不过得分两种情况进行讨论:
- 新增结点在c树上,会导致cur的平衡因子变为-1,parent的平衡因子变为0。
- 新增结点在b树上,会导致cur的平衡因子变为0,parent的平衡因子变为1
- 不管新增结点在谁上,cur_right的平衡因子都为0。
- 总结
- cur_right平衡因子为1,说明新增结点在b树上,会导致cur的平衡因子变为0,parent的平衡因子变为1。
- cur_right的平衡因子为-1,新增结点在c树上,会导致cur的平衡因子变为-1,parent的平衡因子变为0。
- cur_right的平衡因子为0,cur与parent的平衡因子都变为0。
- 不管新增结点在谁上,cur_right的平衡因子都为0。
- 代码实现
void RotateLR(Node* parent){Node* cur = parent->_left;Node* cur_right = cur->_right;int CR_bf = cur_right->_bf;RotateL(cur);RotateR(parent);if (CR_bf == 0){parent->_bf = cur->_bf = cur_right->_bf = 0;}else if(CR_bf == 1){cur->_bf = -1;parent->_bf = cur_right->_bf = 0;}else if (CR_bf == -1){parent->_bf = 1;cur->_bf = cur_right->_bf = 0;}else{cout << __LINE__ << ":" << endl;perror("平衡因子有误");exit(-1);}}
②验证
说明:
- 根据定义验证每颗子树的高度差
- 需要判断当前的右子树的高度差是否等于平衡因子
直接根据平衡因子进行判断,有点监守自盗的感觉,你能保证自己更新的平衡因子就是正确的么?我都不敢保证。
1.求二叉树高度
- 后序遍历
size_t Height(Node* root){if (root == nullptr){return 0;}int LHeight = Height(root->_left);int RHeight = Height(root->_right);return max(LHeight, RHeight) + 1;}
2. 判断是否为AVL树
bool _IsAVLTree(Node* root){if (root == nullptr){return true;}int RHeight = Height(root->_right);int LHeight = Height(root->_left);if (abs(RHeight - LHeight) > 1 || root->_bf != RHeight - LHeight){return false;}return _IsAVLTree(root->_left) && _IsAVLTree(root->_right);}
优化一下:
bool IsAVLTree(){bool is_AVL = true;_IsAVLTree(_root, is_AVL);return is_AVL;}int _IsAVLTree(Node* root,bool& is_AVL){if (root == nullptr){return 0;}int RHeight = _IsAVLTree(root->_right, is_AVL);int LHeight = _IsAVLTree(root->_left, is_AVL);if (abs(RHeight - LHeight) > 1 || root->_bf != RHeight - LHeight){is_AVL = false;}return max(RHeight, LHeight) + 1;}
源码
#include<iostream>
#include<assert.h>
using namespace std;
namespace MY_STL
{template<class Key,class Val>struct AVLTreeNode{typedef AVLTreeNode<Key, Val> Node;AVLTreeNode(const pair<Key,Val>& key = pair<Key,Val>()):_key(key.first),_val(key.second),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}Key _key;Val _val;//三叉链的结构Node* _left;Node* _right;Node* _parent;int _bf;};template<class Key, class Val>class AVLTree{typedef AVLTreeNode<Key, Val> Node;public:AVLTree(){}bool insert(const pair<Key,Val>& val){//第一步:插入操作//如果根节点为空if (_root == nullptr){_root = new Node(val);return true;}else{Node* cur = _root,*parent = _root;while (cur){if (cur->_key > val.first){parent = cur;cur = cur->_left;}else if(cur->_key < val.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(val);if (parent->_key > val.first){parent->_left = cur;}else{parent->_right = cur;}//更新新增结点的_parentcur->_parent = parent;//第二步:更新平衡因子//平衡因子://1. 定义为右子树的高度减去左子树的高度//2. 合法范围为{-1,0,1}//3. 新增结点在左,父节点的平衡因子减1//4. 新增结点在右,父节点的平衡因子加1//5. 当父节点的平衡因子变为0——由-1变0或者1变0时,此时AVL树的高度不变//6. 当父节点的平衡因子变为1或者-1,AVL子树的高度变化,继续向上变化。//7. 当父节点的平衡因子变为2或者-2时,此时需要旋转,进行平衡//8. 当父节点为根节点时,此时需要结束循环。while (cur != _root){//更新平衡因子if (parent->_left == cur){//左减1(parent->_bf)--;}else{//右加1(parent->_bf)++;}//判断平衡因子if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = cur->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//对旋转进行分类讨论//if (parent->_bf == 2 && cur->_bf == 1)//{// //左单旋// RotateL(parent);//}//else if (parent->_bf == -2 && cur->_bf = -1)//{// //右单旋// RotateR(parent);//}//else if (parent->_bf == 2 && cur->_bf == -1)//{// RotateRL(parent);//}//else if (parent->_bf == -2 && cur->_bf == 1)//{// RotateLR(parent);//}if (parent->_bf == 2){//左单旋if (cur->_bf == 1){RotateL(parent);}else{RotateRL(parent);}}else{//右单旋if (cur->_bf == -1){RotateR(parent);}else{RotateLR(parent);}}//旋转完成,树达到平衡break;}}return true;}}//根据定义进行判断bool IsAVLTree(){bool is_AVL = true;_IsAVLTree(_root, is_AVL);return is_AVL;//return _IsAVLTree(_root);}void Print(){_InOrder(_root);cout << endl;}//根据平衡因子进行判断//bool IsAVLTree()//{// return _IsAVLTree(_root);//}private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}//bool _IsAVLTree(Node* root)//{// if (root == nullptr)// return true;// if (root->_bf >= 2 || root->_bf <= -2)// {// return false;// }// else// {// return _IsAVLTree(root->_left) && _IsAVLTree(root->_right);// }//}//bool IsAVLTree()//{// bool is_AVL = true;// _IsAVLTree(_root, is_AVL);// return is_AVL;//}size_t Height(Node* root){if (root == nullptr){return 0;}int LHeight = Height(root->_left);int RHeight = Height(root->_right);return max(LHeight, RHeight) + 1;}int _IsAVLTree(Node* root,bool& is_AVL){if (root == nullptr){return 0;}int RHeight = _IsAVLTree(root->_right, is_AVL);int LHeight = _IsAVLTree(root->_left, is_AVL);if (abs(RHeight - LHeight) > 1 || root->_bf != RHeight - LHeight){is_AVL = false;}return max(RHeight, LHeight) + 1;}bool _IsAVLTree(Node* root){if (root == nullptr){return true;}int RHeight = Height(root->_right);int LHeight = Height(root->_left);if (abs(RHeight - LHeight) > 1 || root->_bf != RHeight - LHeight){return false;}return _IsAVLTree(root->_left) && _IsAVLTree(root->_right);}void RotateLR(Node* parent){Node* cur = parent->_left;Node* cur_right = cur->_right;int CR_bf = cur_right->_bf;RotateL(cur);RotateR(parent);if (CR_bf == 0){parent->_bf = cur->_bf = cur_right->_bf = 0;}else if(CR_bf == 1){cur->_bf = -1;parent->_bf = cur_right->_bf = 0;}else if (CR_bf == -1){parent->_bf = 1;cur->_bf = cur_right->_bf = 0;}else{cout << __LINE__ << ":" << endl;perror("平衡因子有误");exit(-1);}}void RotateRL(Node* parent){Node* cur = parent->_right;Node* cur_left = cur->_left;//CL——CurLeftint CL_bf = cur_left->_bf;RotateR(cur);RotateL(parent);if (CL_bf == 0){cur->_bf = parent->_bf = cur_left->_bf = 0;}else if (CL_bf == 1){parent->_bf = -1;cur->_bf = cur_left->_bf = 0;}else if(CL_bf == -1){cur->_bf = 1;parent->_bf = cur_left->_bf = 0;}else{cout << __LINE__ << ":" << endl;perror("平衡因子有误");exit(-1);}}void RotateL(Node* parent){//画图分析://操作的结点有cur,cur_left,ppnodeNode* cur = parent->_right;Node* cur_left = cur->_left;//将parent的右节点改为cur_leftparent->_right = cur_left;//改变cur_left父节点的转向//cur_left可能为空if (cur_left != nullptr){cur_left->_parent = parent;}//将parent链接在cur的左边//为了更新cur的parent需要保存parent的父节点Node* ppnode = parent->_parent;cur->_left = parent;parent->_parent = cur;//ppnode可能为空if (ppnode == nullptr){//需要修改根节点_root = cur;cur->_parent = nullptr;}else{//改变ppnode的指向if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}//更新平衡因子cur->_bf = parent->_bf = 0;}void RotateR(Node* parent){//操作的结点Node* cur = parent->_left;Node* cur_right = cur->_right;//第一步:将cur_right链接到parent的leftparent->_left = cur_right;//更改cur_right的父节点//注意:cur_right可能为空if (cur_right != nullptr){cur_right->_parent = parent;}//第二步:将parent链接到cur的右结点。//先保存一下parent的父节点Node* ppnode = parent->_parent;cur->_right = parent;parent->_parent = cur;//ppnode为空说明需要修改根节点if (ppnode == nullptr){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}//更新平衡因子cur->_bf = parent->_bf = 0;}Node* _root = nullptr;};
};总结
AVL树还有删除操作,等博主有空再补充,对于AVL树一般来说只需要弄懂一种单旋,一种双旋,再加一些细写处理,代码是不难的,难就难在了分类讨论+画图上。今天的分享就到这里了,如果感觉有所帮助,不妨点个赞鼓励一下吧!
相关文章:

【数据结构】AVL树的插入与验证
文章目录 一、基本概念1.发展背景2.性质 二、实现原理①插入操作1.平衡因子1.1平衡因子的更新1.1.1树的高度变化1.1.2树的高度不变 2. 旋转2.1左旋2.2右旋2.3右左双旋2.4 左右双旋 ②验证1.求二叉树高度2. 判断是否为AVL树 源码总结 一、基本概念 1.发展背景 普通的二叉搜索树…...

9.3.3网络原理(网络层IP)
一.报文: 1.4位版本号:IPv4和IPv6(其它可能是实验室版本). 2.4位首部长度:和TCP一样,可变长,带选项,单位是4字节. 3.8位服务类型 4.16位总长度:IP报头 IP载荷 传输层是不知道载荷长度的,需要网络层来计算. IP报文 - IP报头 IP载荷 TCP报文 TCP载荷 IP载荷(TCP报文) …...

代码随想录算法训练营第四十八天| LeetCode121. 买卖股票的最佳时机、122.买卖股票的最佳时机II、123.买卖股票的最佳时机III
121. 买卖股票的最佳时机 题目描述: 121. 买卖股票的最佳时机. 解法 dp class Solution(object):def maxProfit(self, prices):if not prices:return 0dp0 0# 0表示不持有股票,1表示持有股票dp1 0-prices[0]for i in range(1,len(prices)):# 当前没有股票# 两…...

C++新经典10--vector以及其使用
vector vector类型是一个标准库中的类型,代表一个容器、集合或者动态数组这样一种概念。既然是容器,那就可以把若干个对象放到里面。当然,这些对象的类型必须相同。简单来说,可以把一堆int型数字放到vector容器中去,复…...

std : : vector
一.简介 std::vector 的底层实现通常基于动态数组(dynamic array),它是一种连续分配的内存块,允许元素的快速随机访问。下面是 std::vector 的一些关键特点和底层实现细节: 连续内存块:std::vector 内部使…...
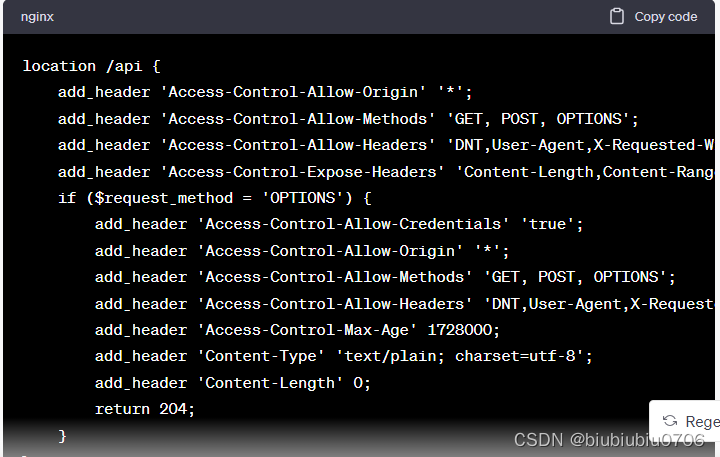
AJAX学习笔记8 跨域问题及解决方案
AJAX学习笔记7 AJAX实现省市联动_biubiubiu0706的博客-CSDN博客 跨域:指一个域名的网页去请求另外一个域名资源.比如百度页面去请求京东页面资源. 同源与不同源三要素:协议,域名,端口 协议一致,域名一致,端口一致.才算是同源.其他一律不同源 新建项目测试: 1.window.open();…...
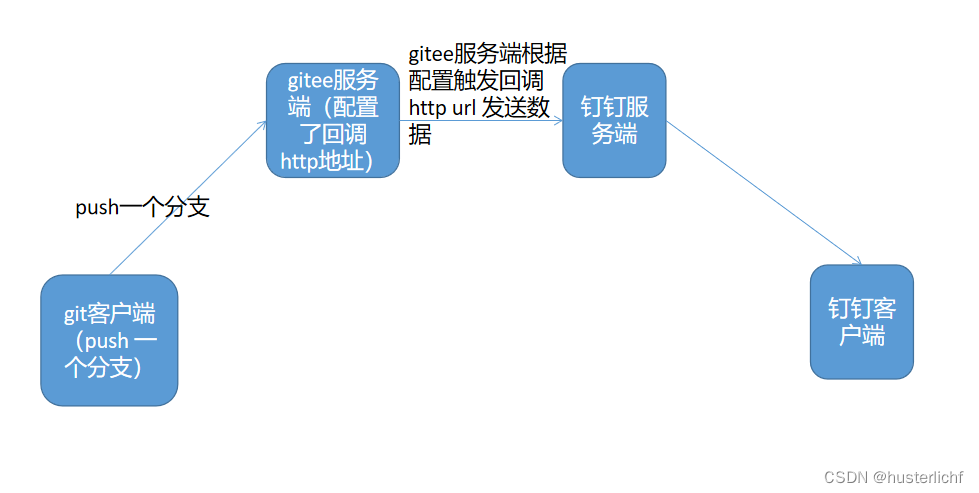
webhook--详解(gitee 推送)
一、简介 webhook 是一种基于 HTTP 的回调函数,可在 2 个应用编程接口(API)之间实现轻量级的事件驱动通信。是一种新型的前后端交互方式,一种对客户端-服务器模式的逆转,在传统方法中,客户端从服务器请求数…...
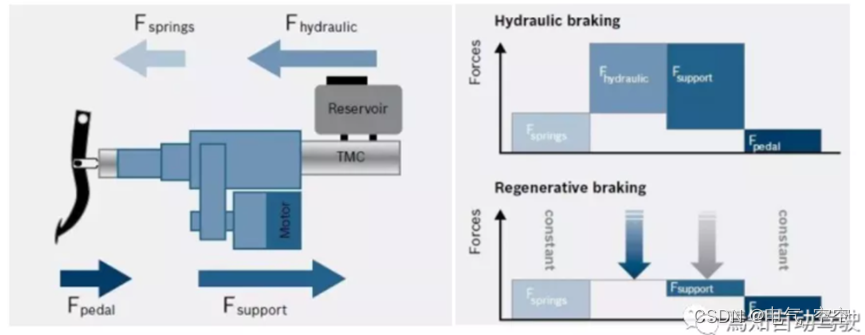
高速路自动驾驶功能HWP功能定义
一、功能定义 高速路自动驾驶功能HWP是指在一般畅通高速公路或城市快速路上驾驶员可以放开双手双脚,同时注意力可在较长时间内从驾驶环境中转移,做一些诸如看手机、接电话、看风景等活动,该系统最低工作速度为60kph。 如上两种不同环境和速度…...

Leetcode113. 路径总和 II
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。 官方题解:力扣(LeetCode)官网 - 全…...

分布式锁之redis实现
docker安装redis 拉取镜像 docker pull redis:6.2.6 查看镜像 启动容器并挂载目录 需要挂在的data和redis.conf自行创建即可 docker run --restart always -d -v /usr/local/docker/redis/redis.conf:/usr/local/etc/redis/redis.conf -v /usr/local/docker/redis/data:/dat…...
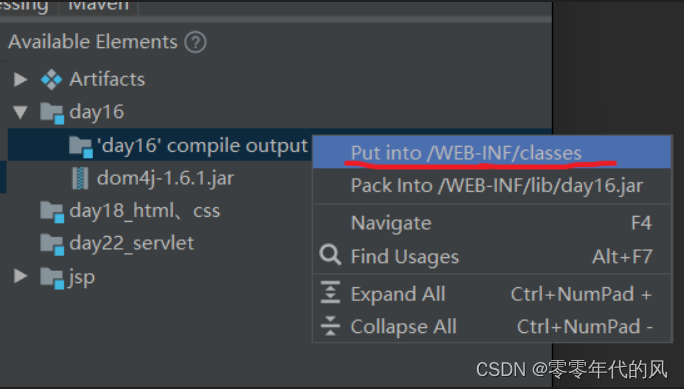
Idea中如何在一个项目中引入其他子模块?
首先在Settings打开Project Structure,然后找到Modules,点击加号点击import module,将需要引进的module引进来。 然后点击Artifacts 可以看到比如说day22…这个是我现在的项目,day16是我需要引入的。那么就在红色横线上面右键点第…...

UDP协议概述
传输层里比较重要的两个协议,一个是 TCP,一个是 UDP。TCP 是面向连接的,UDP 是面向无连接的。 所谓的建立连接,是为了在客户端和服务端维护连接,而建立一定的数据结构来维护双方交互的状态,用这样的数据结…...

Python-tracemalloc-跟踪内存分配
tracemalloc 模块是一个用于对 python 已申请的内存块进行debug的工具。它能提供以下信息: 定位对象分配内存的位置 按文件、按行统计python的内存块分配情况: 总大小、块的数量以及块平均大小。 对比两个内存快照的差异,以便排查内存泄漏 显示前10项 显示内存…...

02 CSS技巧
02 CSS技巧 clip-path 自定义形状,或者使用自带的属性画圆等circle HTML结构 <body><div class"container"></div> </body>CSS结构 使用*polygon*自定义形状 .container {width: 300px;height: 300px;background-color: re…...

Yarn资源调度器
文章目录 一、Yarn资源调度器1、架构2、Yarn工作机制3、HDFS、YARN、MR关系4、作业提交之HDFS&MapReduce 二、Yarn调度器和调度算法1、先进先出调度器(FIFO)2、容量调度器(Capacity Scheduler)3、公平调度器(Fair …...
android上架备案公钥和md5获取工具
最近很多公司上架遇到了一个问题,就是要提供app的备案证明,现在android上架都需要备案了,但是我们的证书都是通过工具生成的,哪里知道公钥和md5那些东西呢?无论安卓备案还是ios备案都需要提供公钥和md5。 包括ios的备案…...
SpringBoot系列(12):SpringBoot集成log4j2日志配置
最近项目上有使用到log4j2日志模板配置,本文简单总结一下之前的学习笔记,如有纰漏之处,请批评指正。 1. log4j2日志依赖 使用log4j2日志模板时,需要引入相关依赖,下边的两种依赖方式均可。 1.1 使用sl4j依赖时 <…...

HTML事件列表
鼠标事件 属性描述DOMonclick当用户点击某个对象时调用的事件句柄。2oncontextmenu在用户点击鼠标右键打开上下文菜单时触发ondblclick当用户双击某个对象时调用的事件句柄。2onmousedown鼠标按钮被按下。2onmouseenter当鼠标指针移动到元素上时触发。2onmouseleave当鼠标指针…...
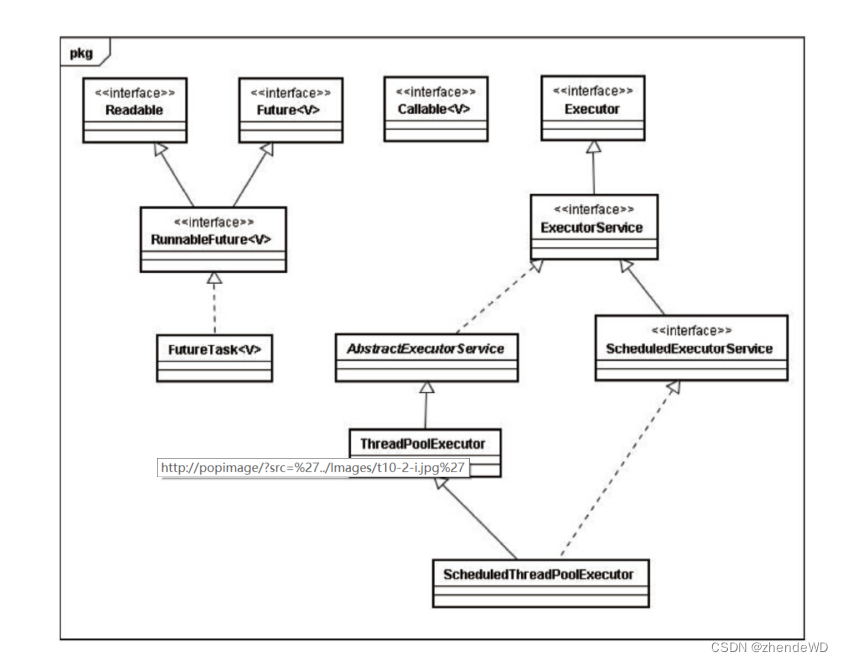
并发-Executor框架笔记
Executor框架 jdk5开始,把工作单元与执行机制分离开来,工作单元包括Runable和Callable,执行机制由Executor框架来提供。 Executor框架简介 Executor框架的两级调度模型 Java线程被一对一映射为本地操作系统线程 java线程启动会创建一个本…...
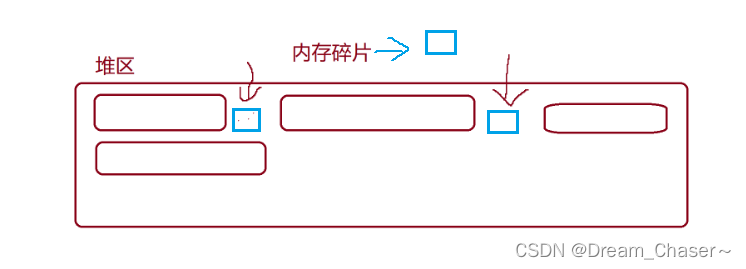
【C进阶】分析 C/C++程序的内存开辟与柔性数组(内有干货)
前言: 本文是对于动态内存管理知识后续的补充,以及加深对其的理解。对于动态内存管理涉及的大部分知识在这篇文章中 ---- 【C进阶】 动态内存管理_Dream_Chaser~的博客-CSDN博客 本文涉及的知识内容主要在两方面: 简单解析C/C程序…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
