归并排序-面试例子
小数和问题
描述
在一个数组中,一个数左边比它小的数的总和,叫数的小和,所有数的小和累加起来,叫数组小和。求数组小和。
例子
5 2 6 1 7 小和原始的求法是:任何一个数左边比它小的数累加起来。 5左边比它小数累加:0 2左边比它小数累加:0 6左边比它小数累加:5 + 2 = 7 1左边比它小数累加:0 7左边比它小数累加:5 + 2 + 6 + 1 = 14 总共21。
思路
如果左侧某数a比右侧某数b小,则在求b的小和的时候,肯定会累加一个a,即sum+=a。 反过来,在遍历到a的时候,如果我们知道右侧有几个数比a大,则可以提前知道会累加几个a 使用归并排序时恰好有左右对比操作,所以使用归并排序来做 即: 每个数右边比它大的数的个数 * 这个数自身 所以: 在原来归并排序的基础上,增加一个ans用于记录结果 在进行归并时左侧<右侧时产生小数 n * number
小和求法还可以是:每个数右边比它大的数的个数 * 这个数自身5 2 6 1 7 5的右边比它大的数的个数:2个(6和7),所以产生:2个 * 5 = 10 2的右边比它大的数的个数:2个(6和7),所以产生:2个 * 2 = 4 6的右边比它大的数的个数:1个(7),所以产生:1个 * 6 = 6 1的右边比它大的数的个数:1个(7),所以产生:1个 * 1 = 1 7的右边比它大的数的个数:0个,所以产生:0个 * 7 = 0 总共21。
code
非递归
public static int smallSum(int [] arr){if(arr == null || arr.length <2)return 0;int [] help = new int[arr.length];int step = 1;int N = arr.length;int L = 0;int ans = 0;while (step < N){L = 0;while (L < N){//左组最后一个数位置int m = L + step - 1;if(m >= N){break;}if(step >= N - L){break;}int R = Math.min(m+step,N-1);ans += merge(arr,L,m,R,help);L = R + 1;}if(step > N/2){break;}step <<= 1;}return ans;}public static int merge(int[] arr,int l,int m,int r,int [] help){//help indexint i = 0;//p1 左侧开始index,p2 右侧开始indexint p1 = l;int p2 = m+1;//结果保存int ans = 0;while (p1 <= m && p2 <= r){ans += arr[p1]<arr[p2]?arr[p1] *(r-p2+1):0;help[i++] = arr[p1]<arr[p2]?arr[p1++]:arr[p2++];}while (p1 <= m){help[i++] = arr[p1++];}while (p2 <= r){help[i++] = arr[p2++];}for (i = 0; i < r-l+1 ; i++) {arr[l+i] = help[i];}return ans;}递归
public static int progress(int [] arr,int l,int r,int [] help){if(l == r)return 0;int m = l + ((r -l) >> 1);return progress(arr,l,m,help)+ progress(arr,m+1,r,help)+ merge(arr,l,m,r,help);}逆序对问题
描述
一个数组中,左边的数比右边的数大,求有多少个这样的组合
比如 [3,1,0,4,3,1] 有7个逆序对,分别是
(3,1),(3,0),(3,1)
(1,0)
(4,3),(4,1)
(3,1)
code
//递归public static int reversePair(int [] arr){if(arr == null || arr.length <2)return 0;return progress(arr,0,arr.length -1);}public static int progress(int [] arr,int l,int r){if(l == r)return 0;int m = l + ((r-l)>>1);return progress(arr,l,m)+progress(arr,m+1,r)+merge(arr,l,m,r);}//非递归public static int reversePair2(int [] arr){if(arr == null || arr.length < 2)return 0;int ans = 0;int L = 0;int N = arr.length;int step = 1;while (step < N){L = 0;while (L < N){if(L+step >= N)break;int m = L + step - 1;if(m >= N)break;int r = Math.min(N-1,m+step);int temp = merge(arr,L,m,r);ans += temp;L = r + 1;}if(step > N/2)break;step <<= 1;}return ans;}public static int merge(int [] arr,int L,int M,int R){// 先算有多少逆序对// 和归并过程分离int res = 0;int p = M + 1;for (int i = L; i <= M; i++) {while (p <= R && arr[i] > arr[p]) {p++;}res += p - (M + 1);}// 下面完全和归并排序一样int[] help = new int[R - L + 1];int i = 0;int p1 = L;int p2 = M + 1;while (p1 <= M && p2 <= R) {help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];}// 要么p1越界了,要么p2越界了while (p1 <= M) {help[i++] = arr[p1++];}while (p2 <= R) {help[i++] = arr[p2++];}for (i = 0; i < help.length; i++) {arr[L + i] = help[i];}return res;}左边大于右边倍数的数
描述
在一个数组中, 对于每个数num,求有多少个后面的数 * 2 依然<num,求总个数 比如:[3,1,7,0,2] 3的后面有:1,0 1的后面有:0 7的后面有:0,2 0的后面没有 2的后面没有 所以总共有5个
思路
右边有多少个数*2比左边的数小 在归并排序过程中,分组后左侧有序,右侧有序,在进行左右侧合并时,统计验证关系【2倍关系】 这样可以得到该左侧位置相对于右侧位置的2倍关系统计和
code
//递归public static int biggerThatRightTwice(int []arr){if(arr == null || arr.length<2){return 0;}return progress(arr,0,arr.length-1);}public static int progress(int[] arr,int l,int r){if(l == r){return 0;}int m = l + ((r-l)>>1);System.out.println("l,m,r:"+l+","+m+","+r);return progress(arr,l,m)+progress(arr,m+1,r)+merge(arr,l,m,r);}//非递归public static int biggerThatRightTwice2(int [] arr){if(arr == null || arr.length <2)return 0;int L = 0;int step = 1;int N = arr.length;int ans = 0;while (step < N){L = 0;while (L < N){if(step >= N-L)break;int m = L + step - 1;if(m >= N)break;int r = Math.min(m+step,N-1);ans += merge(arr,L,m,r);L = r + 1;}if(step > N/2)break;step <<=1;}return ans;}public static int merge(int[] arr,int l,int m,int r){//[l,m] [m+1,r]进行归并,其中[l,m],[m+1,r]分别已经有序//先计算int p1 = l,p2 = m+1;int ans = 0;//左侧遍历lwhile (p1 <= m){//右侧遍历while (p2 <= r){//如果左侧 > 右侧 * 2,则继续判断,知道不满足条件//当不满足条件时,则右侧从开始位置m+1到p2位置为p1满足条件的数if(arr[p1] > arr[p2] *2){p2++;}else{break;}}//p2 - (m+1) => [m+1,p2) 即从m+1到p2个元素个数,不包含p2ans += (p2 - (m+1));p1++;}//再进行归并int [] help = new int[r-l+1];int i = 0;p1 = l;p2 = m+1;while (p1<=m && p2<=r){help[i++] = arr[p1]<arr[p2]?arr[p1++]:arr[p2++];}while (p1<=m){help[i++] = arr[p1++];}while (p2<=r){help[i++] = arr[p2++];}for(i=0;i<help.length;i++){arr[l+i] = help[i];}return ans;}
相关文章:

归并排序-面试例子
小数和问题 描述 在一个数组中,一个数左边比它小的数的总和,叫数的小和,所有数的小和累加起来,叫数组小和。求数组小和。 例子 5 2 6 1 7 小和原始的求法是:任何一个数左边比它小的数累加起来。 5左边比它小数累加…...
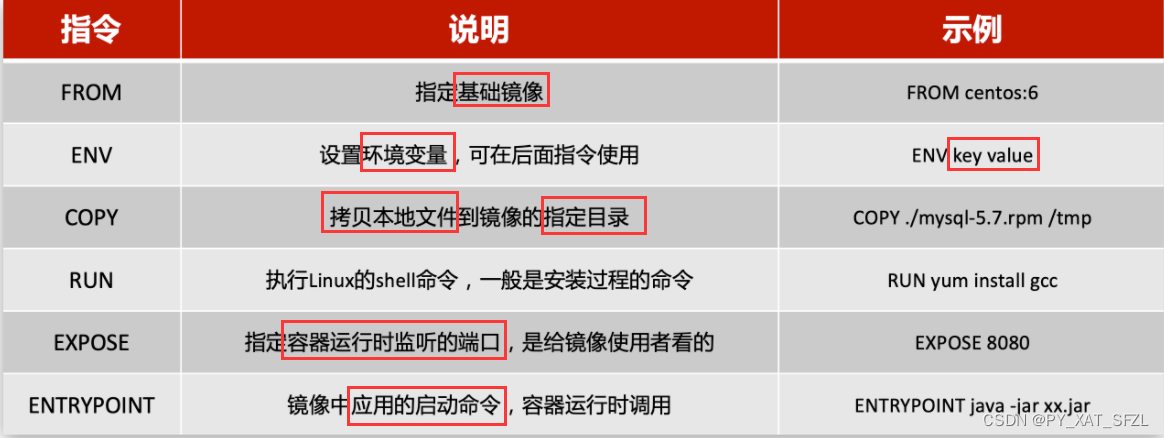
docker 生成镜像的几个问题
docker 生成镜像的几个问题 根据jdk8.tar.gz 打包Jdk8 镜像失败运行镜像报错差不多是网络ip错误,在网上说重启docker即可解决运行mysql5.7.25 镜像失败向daemon.json文件添加内容导致docker重启失败docker run 命令常用参数根据jdk8.tar.gz 打包Jdk8 镜像失败 首选做准备工作…...

云计算时代的采集利器
大家好!在今天的知识分享中,我们将探讨一个在云计算环境中的爬虫应用利器——独享IP。如果你是一名爬虫程序员,或者对数据采集和网络爬虫有浓厚的兴趣,那么这篇文章将向你展示独享IP在云计算环境下的应用价值。 1. 什么是独享IP&…...

【Unity编辑器扩展】| Inspector监视器面板扩展
前言【Unity编辑器扩展】| Inspector监视器面板扩展一、ContextMenu和ContextMenuItem二、Custom Editors 自定义编辑器三、Property Drawer 属性绘制器总结前言 前面我们介绍了Unity中编辑器扩展的一些基本概念及基础知识,还有编辑器扩展中用到的相关特性Attribute介绍。后面…...

Redis配置
关系型数据库和非关系型数据库 ①了解关系和非关系 关系型数据库 一个结构化的数据库,创建在关系模型基础上,一般面向于记录,包括Oracle、MySQL、SQL Server、Microsoft Access、DB2、postgreSQL等 非关系型数据库 除了主流的关系型数据库…...

CSDN每日一练 |『小艺照镜子』『Ctrl+X,Ctrl+V』『括号上色』2023-09-11
CSDN每日一练 |『小艺照镜子』『Ctrl+X,Ctrl+V』『括号上色』2023-09-11 一、题目名称:小艺照镜子二、题目名称:Ctrl+X,Ctrl+V三、题目名称:括号上色一、题目名称:小艺照镜子 时间限制:1000ms内存限制:256M 题目描述: 已知字符串str。 输出字符串str中最长回文串的长度…...

React 全栈体系(四)
第二章 React面向组件编程 六、组件的生命周期 1. 效果 需求:定义组件实现以下功能: 让指定的文本做显示 / 隐藏的渐变动画从完全可见,到彻底消失,耗时2S点击“不活了”按钮从界面中卸载组件 <!DOCTYPE html> <html lang"e…...

各种UI库使用总结
各种UI库使用总结 工作了这么年,使用了一些UI库,简单的总结一下,UI库也是五花八门,根据自己的产品,应用场景吧,没有绝对合适的,各有各的应用场景吧! QT 这几年前后在一些嵌入式上…...
2023Web前端开发面试手册
HTML基础 1. HTML 文件中的 DOCTYPE 是什么作用? HTML超文本标记语言: 是一个标记语言, 就有对应的语法标准 DOCTYPE 即 Document Type,网页文件的文档类型标准。 主要作用是告诉浏览器的解析器要使用哪种 HTML规范 或 XHTML规范…...
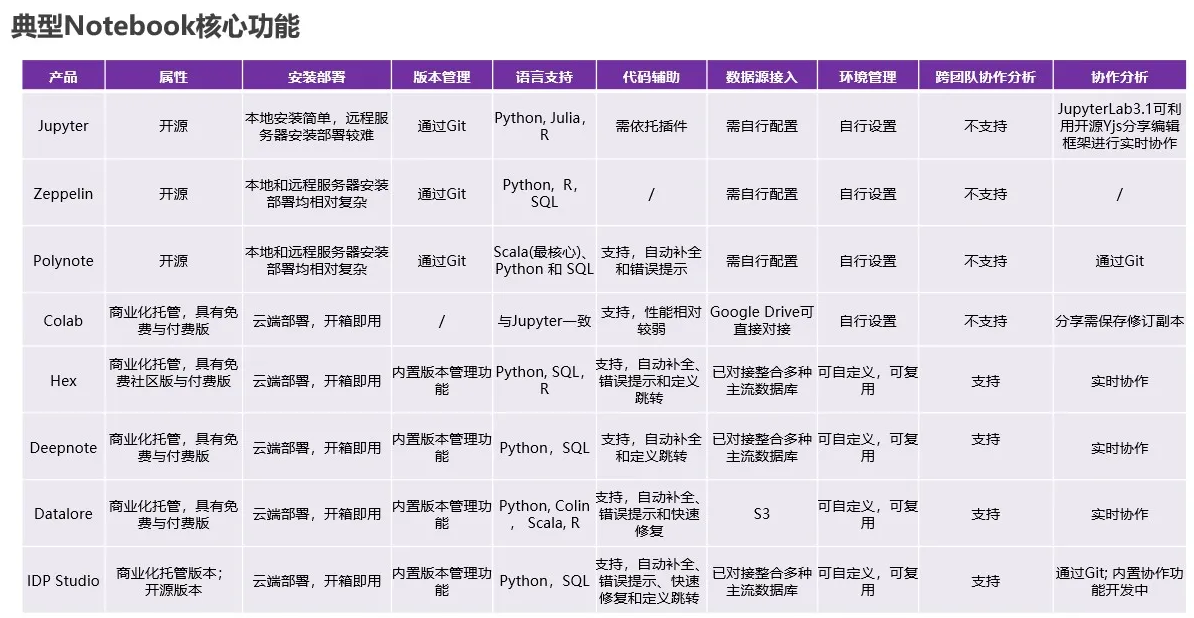
一文了解数据科学Notebook
编者按: 主要介绍什么是Notebook,Notebook在数据科学领域的应用的重要性与优势,以及数据科学家/算法团队在选择Notebook时需考虑哪些关键因素。同时,基于Notebook的筛选考量维度,对常见的Notebook进初步对比分析&#…...

2020年12月 C/C++(二级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C++编程(1~8级)全部真题・点这里 第1题:数组指定部分逆序重放 将一个数组中的前k项按逆序重新存放。例如,将数组8,6,5,4,1前3项逆序重放得到5,6,8,4,1。 时间限制:1000 内存限制:65536 输入 输入为两行: 第一行两个整数,以空格分隔,分别为数组元素的个数n(1 < n…...

关于ChatGPT的个人的一些观点
问题 1 Q: 你认为ChatGPT是一款非常有用的工具吗? A: 我认为ChatGPT是一款非常有用的工具。它可以帮助人们解决各种问题,包括技术问题、心理问题、生活问题等等。同时,ChatGPT也可以成为人们分享想法和交流的平台,增强人与人之间…...
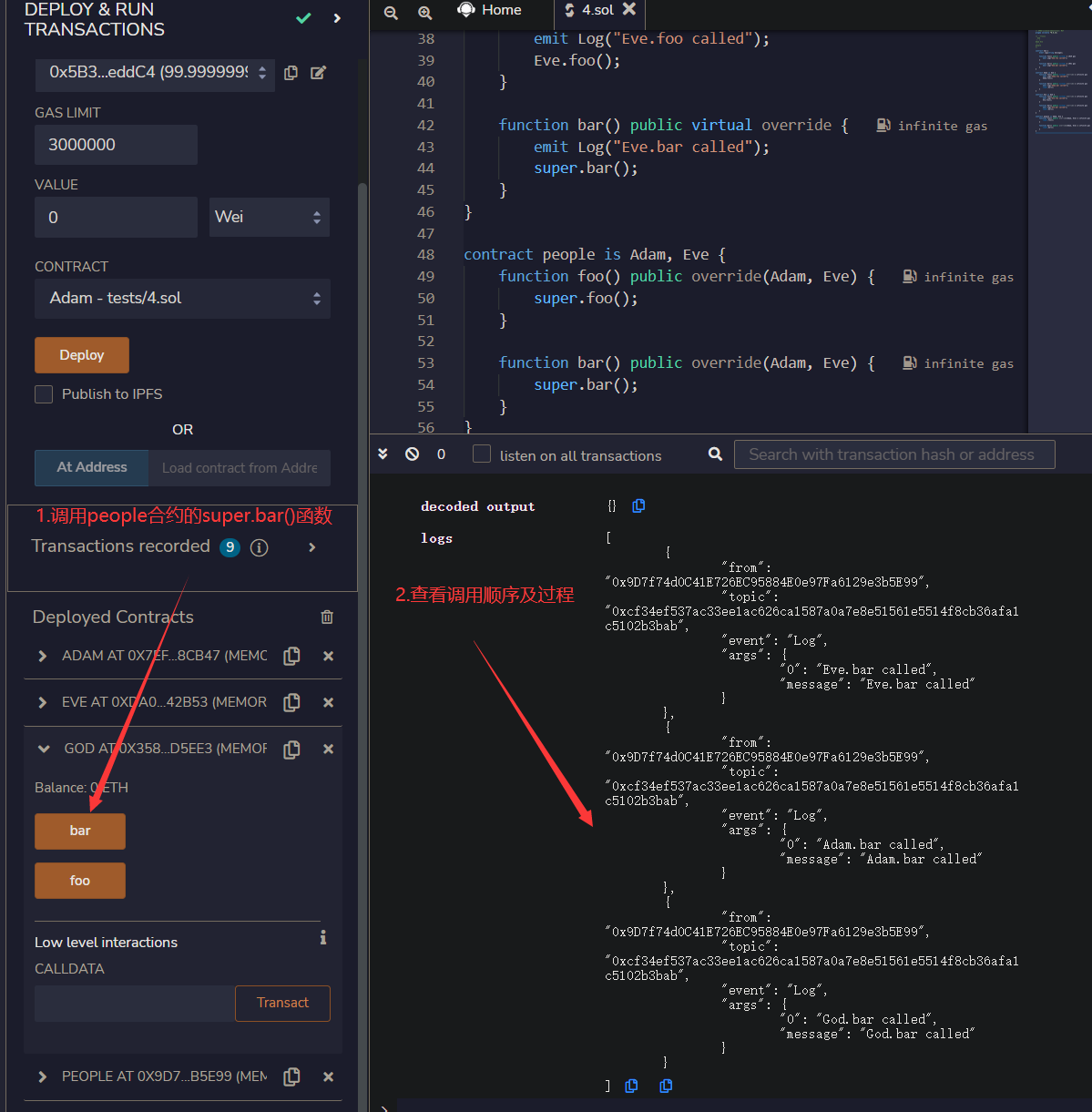
Solidity 小白教程:13. 继承
Solidity 小白教程:13. 继承 这一讲,我们介绍solidity中的继承(inheritance),包括简单继承,多重继承,以及修饰器(modifier)和构造函数(constructorÿ…...

队列(Queue)的顶级理解
目录 1.队列(Queue) 的概念 2.单链表模拟实现队列 2.1创建队列 2.2入队列 2.3判断是否为空 2.4出队列 2.5获取队头元素 2.6完整代码: 2.7双向链表模拟实现队列代码 3.数组模拟实现队列代码 3.1创建队列 3.2判断是否为满 3.3检查是否为空 3.4插入元素 3…...

选择 Guava EventBus 还是 Spring Framework ApplicationEvent
文章首发地址 Spring Framework ApplicationEvent Spring Framework 的 ApplicationEvent 是 Spring 框架提供的一种事件机制,用于实现发布和订阅事件的功能。它基于观察者模式,允许应用程序内的组件之间进行松耦合的通信。 下面是关于 Spring Frame…...

Linux下go环境安装、环境配置并执行第一个go程序
一、安装 1.Golang对Linux的内核版本要求 GO对Linux内核版本最低要求是 2.6.23,对应要求操作系统版本是: RHEL 6.0CentOS 6.0即,不支持 (RHEL 和 CentOS) 的 (4.x or 5.x)。2.下载golang的代码版本 Golang的官网下载地址:https:…...

自定义Dynamics 365实施和发布业务解决方案 - 5. 高级自定义
本章的目的是探索可应用于Dynamics365的高级自定义。这包括使用插件和自定义工作流活动实现复杂的业务流程。此外,您还将了解如何使用SPKL任务运行器来部署这些,这在第2章中进行了讨论。最后,您还将看到使用Web API查询数据。 准备工作 若要从高级自定义开始,必须首先创建…...

软件测试下的AI之路(2)
😏作者简介:博主是一位测试管理者,同时也是一名对外企业兼职讲师。 📡主页地址:【Austin_zhai】 🙆目的与景愿:旨在于能帮助更多的测试行业人员提升软硬技能,分享行业相关最新信息。…...
)
前端面试的话术集锦第 7 篇:高频考点(浏览器渲染原理 安全防范)
这是记录前端面试的话术集锦第七篇博文——高频考点(浏览器渲染原理 & 安全防范),我会不断更新该博文。❗❗❗ 1. 浏览器渲染原理 注意:该章节都是⼀个⾯试题。 1.1 渲染过程 1.1.1 浏览器接收到HTML⽂件并转换为DOM树 当我们打开⼀个⽹⻚时,浏览器都会去请求对应的…...

打印剪刀手“耶”(V形)
用给定单个字符和首行宽度(奇数), 打印首行宽度为给定奇数“V”字形状)。 (本笔记适合Py 推崇的插件字符串格式化的 coder 翻阅) 【学习的细节是欢悦的历程】 Python 官网:https://www.python.org/ Free:大咖免费“圣经”教程《 python 完全…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
