初高(重要的是高中)中数学知识点综合
1. 集合
1.1 集合的由来和确定性
确定对象构成的整体称为集合(组成集合的元素必须是确定的 ),每个集合内的对象个体成为元素(Element)。确定性: 给定一个集合,任何一个对象是不是这个集合内的元素,就已经确定了。
比如,我国的四大发明,造纸术,印刷术,火药,指南针。就是一个明确的构成,这个集合就是四大发明。
四大发明 = {造纸术,印刷术,火药,指南针}
每个集合内的元素,使用逗号隔开。
元素和集合之间,存在 属于/不属于 两种关系,拿上面的四大发明集合来讲,比如:
造纸术属于四大发明集合;手机不属于四大发明集合;
火药属于四大发明集合;机关枪不属于四大发明集合;
为了方便书写,采用方便的符号形式来进行代替。
属于: ∈ 不属于: ∉
在用上述的例子,替换为符号就是
造纸术 ∈ 四大发明集合;手机 ∉ 四大发明集合;
火药 ∈ 四大发明集合;机关枪 ∉ 四大发明集合;
如果给定一个集合, {大学计算机系所有的高个子学生},那么这就是一个没有办法确定的内容,不能形成一个集合。你没办法明确知道高个子到底是多高。 如果是 {大学计算机系所有身高 > 170的高个子学生},那么这就给我们划分了一个很明确的界限,大于 170 cm 的同学,都可以被划分为高个子学生列表。那么就能形成一个集合。
测试题
1. 大于 3 小于 11 的偶数。 (是)
2. 我国的小河流。 (不是)
3. 所有的正方形。 (是)
4. 本班跑步很快的同学。 (不是)
5. 与1接近的实数的全体。 (不是)
6. 1——10以内的全体质数。 (是)
总结
1. 集合是一个由确定对象构成的整体。
2. 集合内的对象称为元素(Element)。
3. 属于 ∈ / 不属于 ∉
4. 集合的确定性,给定一个集合,任何一个对象是不是这个集合内的元素,就已经确定了。
5. 可见,对于给定一个集合和给定一个对象,这个对象是否为这个集合的元素,只有 “是” 与 “不是”,这两种情况,这就是集合中元素
所具有的确定性。
1.2 集合中元素的特性

-
确定性
借鉴上面。 -
互异性
在集合中,集合内的元素必须是互异的,也就是说,对于一个给定的集合,他的任何两个元素都是不同的。
因为集合中的元素是没有重复现象的,所以任何两个相同的元素在同一集合内,只能算作这个集合中的一个元素。
- 无序性
集合与其中元素的排列次序无关,也就是说集合中的元素是不排序的。
例如: {1, 2} 也可以写成 {2, 1},他们两个是一样的。
1.3 常见数集
1.3.1 学习目标
- 理解常见数集的定义。
- 熟记常见数集的符号。
- 会判断数字与不同数集之间的关系。
1.3.2 自然数(Natural Number) 用以计量事物的件数 : N
自然数英语为 Natural Number, 所以用 大写 N 来表示自然数集。
N = {1, 2, 3, 4, 5, 6, 7...}
在1993年对于自然数集做了重新定义,定义为:
- 不小于 0 的所有整数叫 自然数集 / 非负整数 的集,也就是说,0 也是自然数集内的元素
扩展,在中国大陆2000年后的数学教材,自然数集内都包括 0。
在N后做一些特殊标记也有不同的意义,比如:
- N* : 除0意外的自然数集
- N+ : (+可以在N上面,也可以在N下面)正自然数集。
- 以此类推…
1.3.2 整数集(Whole Number): Z
整数并没有用 W 来表示整数集,有一种说法是:德国女数学家,诺特 (1882-1935)德意志数学家,抽象代数的奠基人,她提出的整数环对于整数有重大的意义 所以整数取得是德语 Zahlen(支付,数字)的首字母,Z。
Z = {0, 1, -1, 2, -2....}
1.3.3 分数 (两个整数之比 — 商)
分数,指的是两个整数之比,古希腊数学家毕达哥拉斯提出了万物皆数的概念,还发现了著名的黄金比例。他们认为,整数和分数,就可以解释整个世界了。
1.3.4 有理数:两个整数之比 — 商(Quotient) : Q
所以,有理数采用商的首字母,Q来表示有理数集。准确来说。有理数包括整数和分数
- Q = {整数和非零整数的比}
整数也可以表示成 9/1 (一分之九),8/1,5/1。 分数也可以表示为, 1/2, 3/8, 1/3
1.3.5 无理数:根号二是有理数吗?
并不是,常见的无理数有,开不尽的根号。 根号3,根号5,根号7,根号9.1 …, 无限不循环小数 Π = 3.1415926535…,自然数e等。不过到目前为止,无理数还没有统一的字幕表示。所有的有理数 + 无理数就是实数。
1.3.6 实数(Real Number):R
实数集是所有的有理数 + 无理数,实数集是目前所学的最大的数集。我们所有学习过的数字都在这个集合里面。
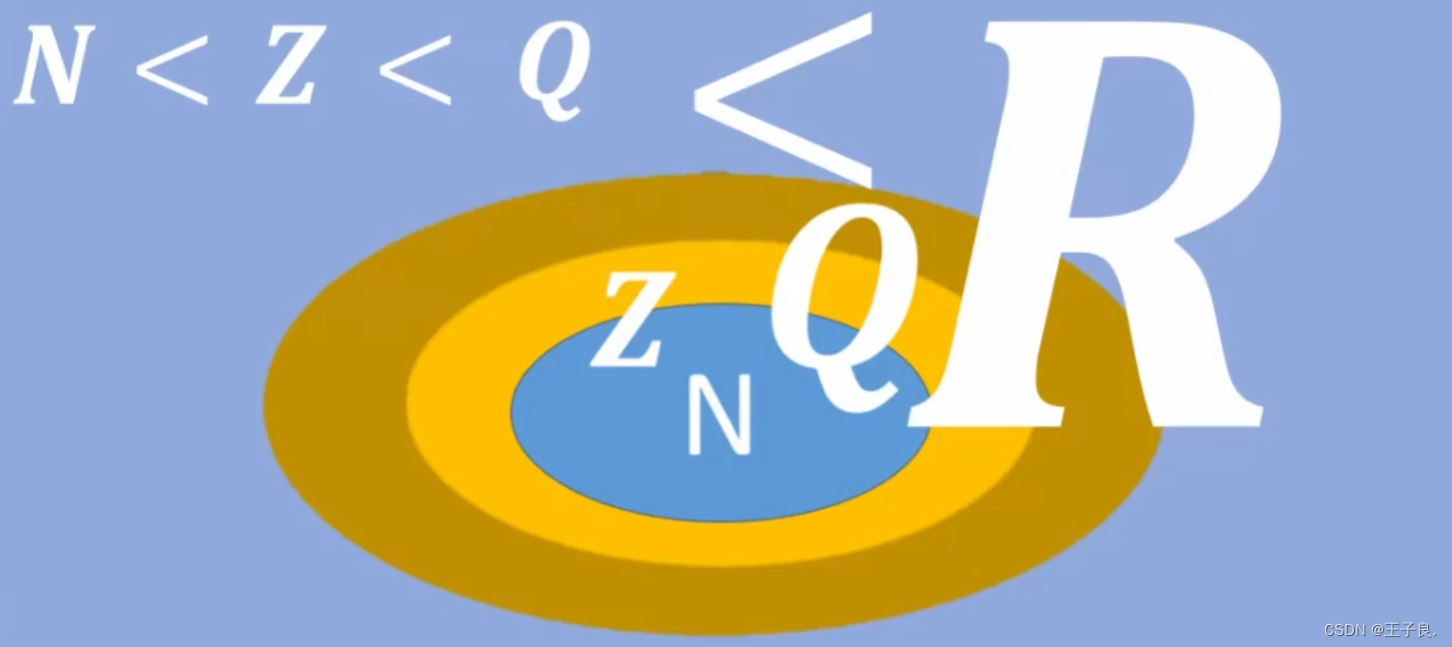
1.3.7 练习题
用符号 “∈” 或者 “∉”填空。
1. 5__N, -5__N, 0__N2. 3__Z, -3__Z, 3.1__Z3. 3.14__Q, Π__Q, 根号2__Q4. Π__R, 3.1__R, 根号三__R
答案
N是自然数集,大于切等于0的整数都是数集内的内容1. ∈,∉,∈Z是整数集,大于小于等于0的所有整数都属于集合内的内容。2. ∈,∈,∉Q是有理数集,也就是两数之比和所有的整数(小数,分数,正整数,负整数,0)3. ∈,∉,∉R是实数集,包括了N,Z,Q,无理数集,是学习过的最大的数集4. ∈,∈,∈
特殊符号集
1. 0__N+, 0__Z+, 0__R*
2. -3__Z+, -3__Z-, -3__Z*
答案
在数集后面跟 + 表示数集内的所有正数对象, - 表示所有的复数对象,R表示0除外的所有对象
3. ∉,∉,∉
4. ∉,∈,∈
1.3.8 总结
学习了各个数集。总结内容如下
- N(自然数集) < Z(整数集) < Q(有理数集) < R(实数集),实际上是不能这样表示的,需要稍微改造一下。
- N(自然数集) ∈ Z(整数集) ∈ Q(有理数集) ∈ R(实数集)
1.4 集合的表示方法
相关文章:
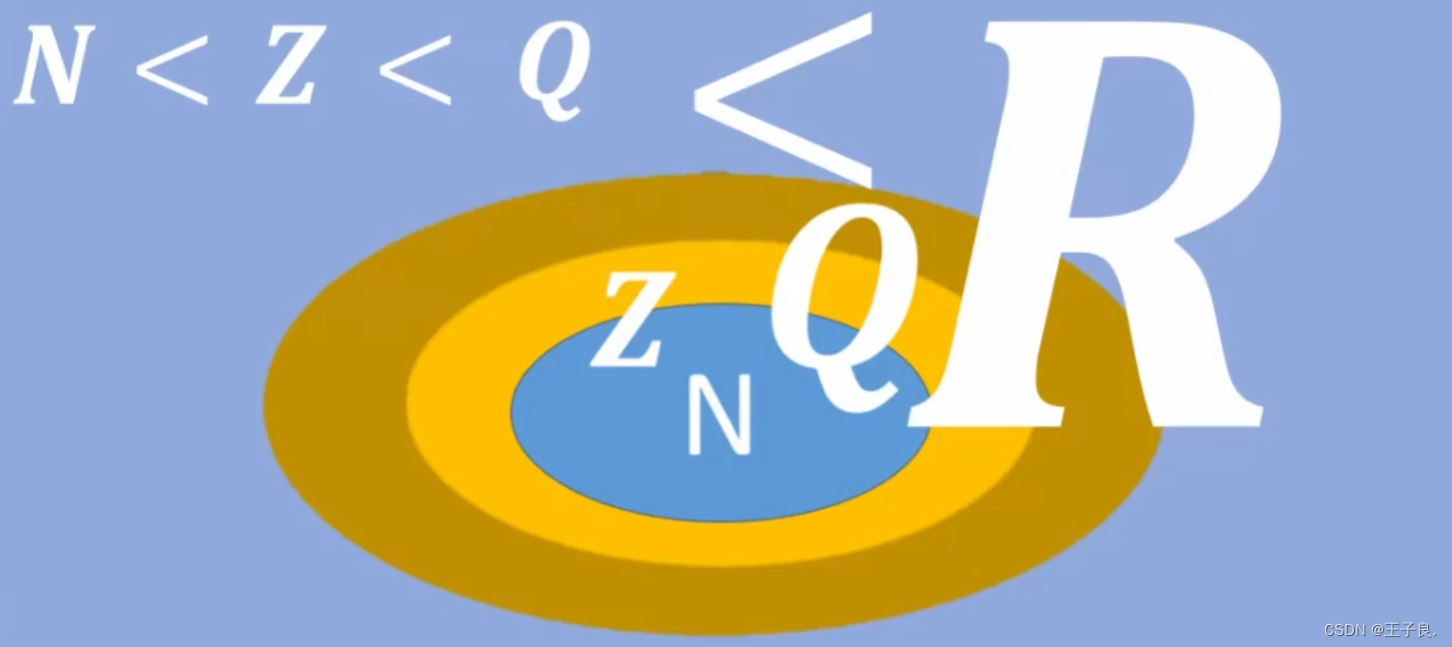
初高(重要的是高中)中数学知识点综合
1. 集合 1.1 集合的由来和确定性 确定对象构成的整体称为集合(组成集合的元素必须是确定的 ),每个集合内的对象个体成为元素(Element)。确定性: 给定一个集合,任何一个对象是不是这个集合内的元素,就已经确…...
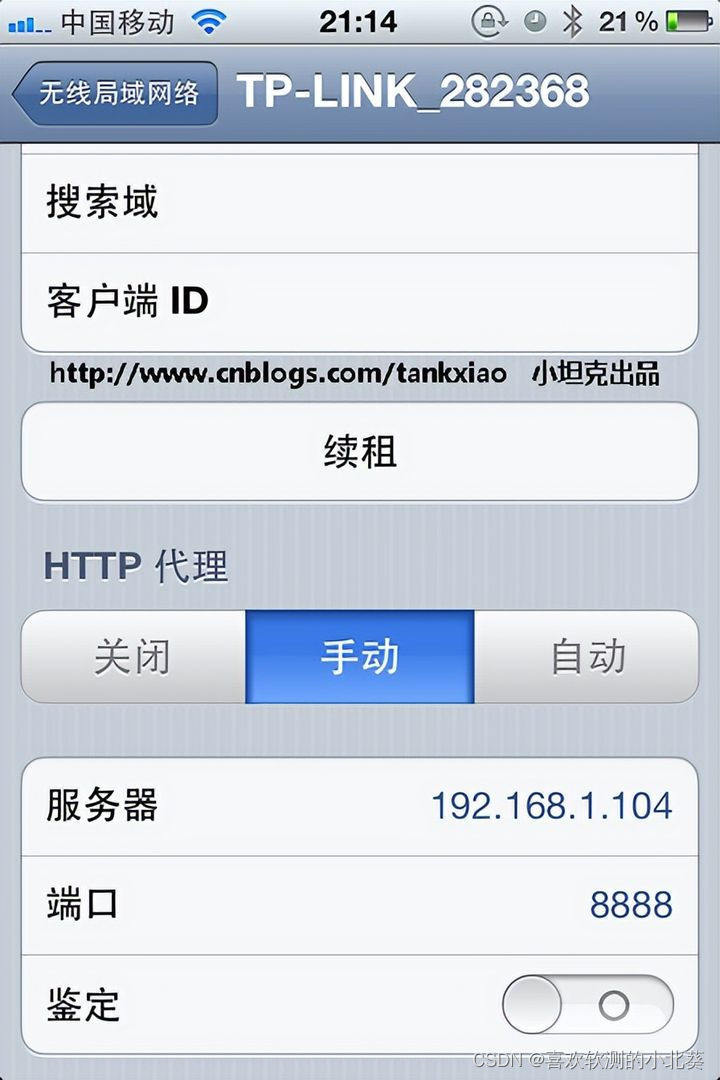
Fiddler 系列教程(二) Composer创建和发送HTTP Request跟手机抓包
Fiddler Composer介绍 Composer的官方帮助文档:http://www.fiddler2.com/fiddler/help/composer.asp Fiddler的作者把HTTP Request发射器取名叫Composer(中文意思是:乐曲的创造者), 很有诗意 Fiddler Composer的功能就是用来创建HTTP Request 然后发送…...

淘宝平台开放接口API接口
淘宝平台开放接口API接口是指淘宝平台提供给第三方开发者的一组接口,用于实现与淘宝平台的数据交互和功能扩展。通过API接口,第三方开发者可以获取淘宝平台上的商品信息、订单信息、用户信息等数据,也可以实现商品的发布、订单的创建和支付等…...

缓存夺命连环问
1. 为什么要用缓存? 用缓存,主要有两个用途:高性能、高并发。 高性能 假设这么个场景,你有个操作,一个请求过来,吭哧吭哧你各种乱七八糟操作 MySQL,半天查出来一个结果,耗时 600m…...

模型生成自动化测试用例
自动产生的测试用例本就应该由程序自动执行,这其实也就是NModel推荐的模式。先回过头来看看文章中制作的模型,模型里面将登录、注销、用户名以及密码等要素都抽象出来了,而NModel是以这些抽象出来的动作(登录、注销)和…...

归并排序-面试例子
小数和问题 描述 在一个数组中,一个数左边比它小的数的总和,叫数的小和,所有数的小和累加起来,叫数组小和。求数组小和。 例子 5 2 6 1 7 小和原始的求法是:任何一个数左边比它小的数累加起来。 5左边比它小数累加…...
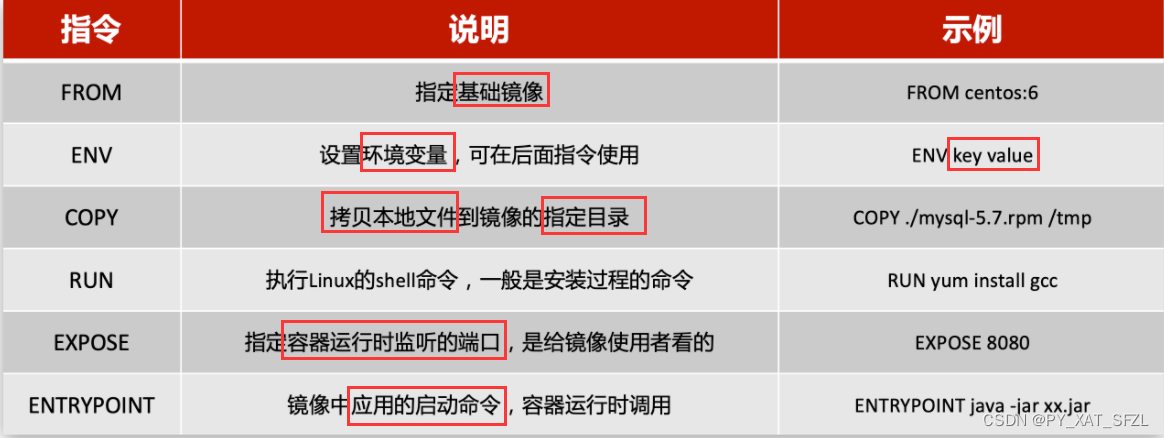
docker 生成镜像的几个问题
docker 生成镜像的几个问题 根据jdk8.tar.gz 打包Jdk8 镜像失败运行镜像报错差不多是网络ip错误,在网上说重启docker即可解决运行mysql5.7.25 镜像失败向daemon.json文件添加内容导致docker重启失败docker run 命令常用参数根据jdk8.tar.gz 打包Jdk8 镜像失败 首选做准备工作…...

云计算时代的采集利器
大家好!在今天的知识分享中,我们将探讨一个在云计算环境中的爬虫应用利器——独享IP。如果你是一名爬虫程序员,或者对数据采集和网络爬虫有浓厚的兴趣,那么这篇文章将向你展示独享IP在云计算环境下的应用价值。 1. 什么是独享IP&…...

【Unity编辑器扩展】| Inspector监视器面板扩展
前言【Unity编辑器扩展】| Inspector监视器面板扩展一、ContextMenu和ContextMenuItem二、Custom Editors 自定义编辑器三、Property Drawer 属性绘制器总结前言 前面我们介绍了Unity中编辑器扩展的一些基本概念及基础知识,还有编辑器扩展中用到的相关特性Attribute介绍。后面…...

Redis配置
关系型数据库和非关系型数据库 ①了解关系和非关系 关系型数据库 一个结构化的数据库,创建在关系模型基础上,一般面向于记录,包括Oracle、MySQL、SQL Server、Microsoft Access、DB2、postgreSQL等 非关系型数据库 除了主流的关系型数据库…...

CSDN每日一练 |『小艺照镜子』『Ctrl+X,Ctrl+V』『括号上色』2023-09-11
CSDN每日一练 |『小艺照镜子』『Ctrl+X,Ctrl+V』『括号上色』2023-09-11 一、题目名称:小艺照镜子二、题目名称:Ctrl+X,Ctrl+V三、题目名称:括号上色一、题目名称:小艺照镜子 时间限制:1000ms内存限制:256M 题目描述: 已知字符串str。 输出字符串str中最长回文串的长度…...

React 全栈体系(四)
第二章 React面向组件编程 六、组件的生命周期 1. 效果 需求:定义组件实现以下功能: 让指定的文本做显示 / 隐藏的渐变动画从完全可见,到彻底消失,耗时2S点击“不活了”按钮从界面中卸载组件 <!DOCTYPE html> <html lang"e…...

各种UI库使用总结
各种UI库使用总结 工作了这么年,使用了一些UI库,简单的总结一下,UI库也是五花八门,根据自己的产品,应用场景吧,没有绝对合适的,各有各的应用场景吧! QT 这几年前后在一些嵌入式上…...
2023Web前端开发面试手册
HTML基础 1. HTML 文件中的 DOCTYPE 是什么作用? HTML超文本标记语言: 是一个标记语言, 就有对应的语法标准 DOCTYPE 即 Document Type,网页文件的文档类型标准。 主要作用是告诉浏览器的解析器要使用哪种 HTML规范 或 XHTML规范…...
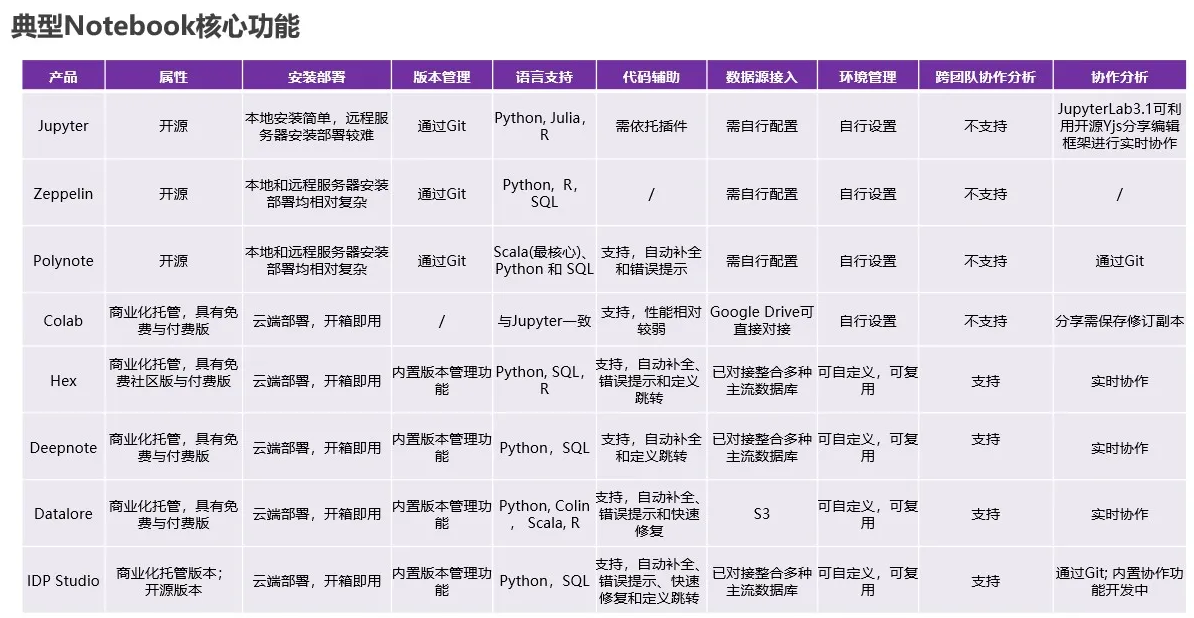
一文了解数据科学Notebook
编者按: 主要介绍什么是Notebook,Notebook在数据科学领域的应用的重要性与优势,以及数据科学家/算法团队在选择Notebook时需考虑哪些关键因素。同时,基于Notebook的筛选考量维度,对常见的Notebook进初步对比分析&#…...

2020年12月 C/C++(二级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C++编程(1~8级)全部真题・点这里 第1题:数组指定部分逆序重放 将一个数组中的前k项按逆序重新存放。例如,将数组8,6,5,4,1前3项逆序重放得到5,6,8,4,1。 时间限制:1000 内存限制:65536 输入 输入为两行: 第一行两个整数,以空格分隔,分别为数组元素的个数n(1 < n…...

关于ChatGPT的个人的一些观点
问题 1 Q: 你认为ChatGPT是一款非常有用的工具吗? A: 我认为ChatGPT是一款非常有用的工具。它可以帮助人们解决各种问题,包括技术问题、心理问题、生活问题等等。同时,ChatGPT也可以成为人们分享想法和交流的平台,增强人与人之间…...
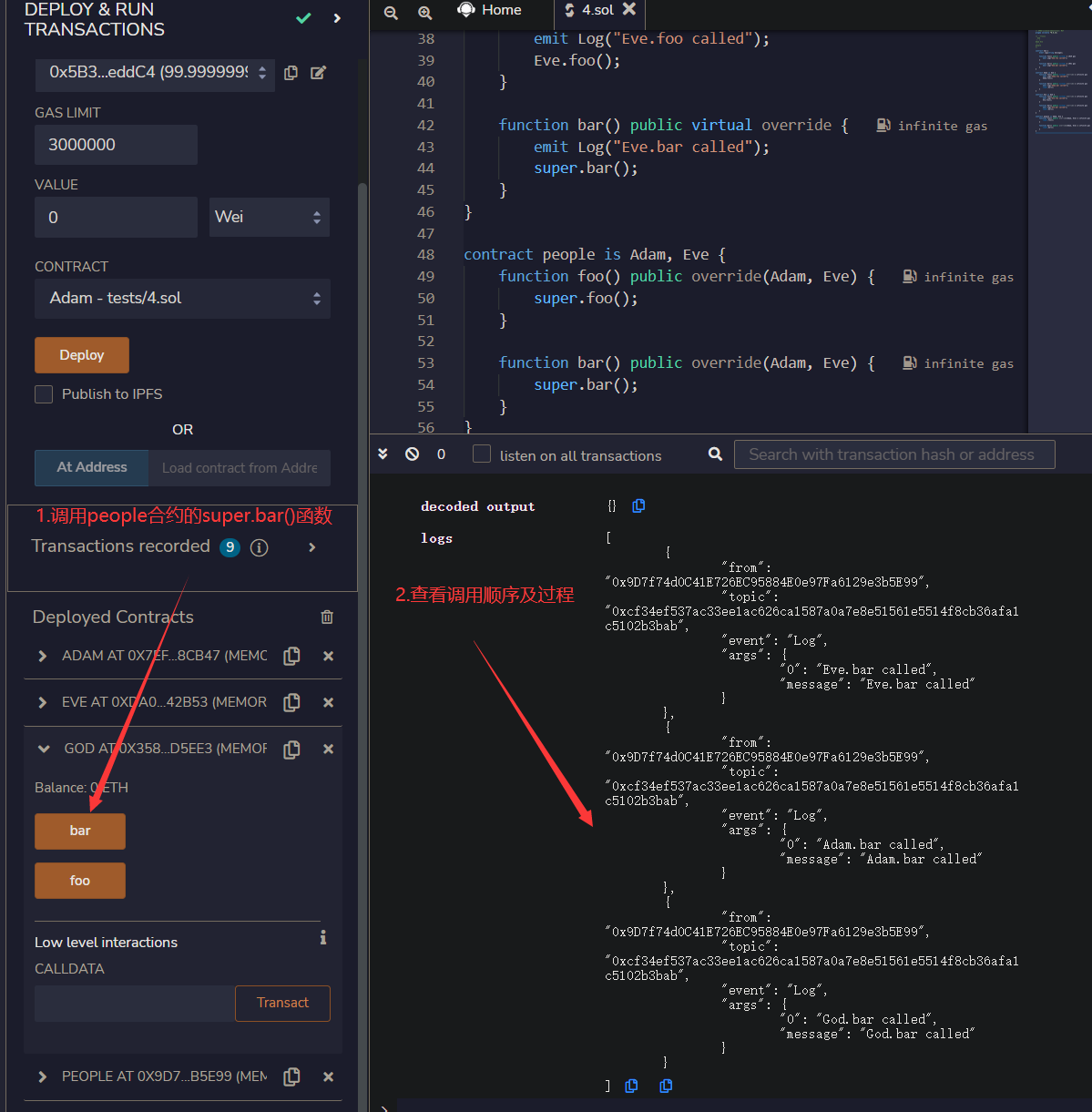
Solidity 小白教程:13. 继承
Solidity 小白教程:13. 继承 这一讲,我们介绍solidity中的继承(inheritance),包括简单继承,多重继承,以及修饰器(modifier)和构造函数(constructorÿ…...

队列(Queue)的顶级理解
目录 1.队列(Queue) 的概念 2.单链表模拟实现队列 2.1创建队列 2.2入队列 2.3判断是否为空 2.4出队列 2.5获取队头元素 2.6完整代码: 2.7双向链表模拟实现队列代码 3.数组模拟实现队列代码 3.1创建队列 3.2判断是否为满 3.3检查是否为空 3.4插入元素 3…...

选择 Guava EventBus 还是 Spring Framework ApplicationEvent
文章首发地址 Spring Framework ApplicationEvent Spring Framework 的 ApplicationEvent 是 Spring 框架提供的一种事件机制,用于实现发布和订阅事件的功能。它基于观察者模式,允许应用程序内的组件之间进行松耦合的通信。 下面是关于 Spring Frame…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...
