How Language Model Hallucinations Can Snowball
本文是LLM系列文章,针对《How Language Model Hallucinations Can Snowball》的翻译。
语言模型幻觉是如何产生雪球的
- 摘要
- 1 引言
- 2 为什么我们期待幻觉像滚雪球一样越滚越大?
- 3 实验
- 4 我们能防止雪球幻觉吗?
- 5 相关工作
- 6 结论
- 局限性
摘要
在实际应用中使用语言模型的一个主要风险是它们容易产生错误陈述的幻觉。幻觉通常归因于LMs中的知识差距,但我们假设,在某些情况下,当证明先前产生的幻觉时,LMs会输出他们可以单独识别为不正确的虚假声明。我们构建了三个问答数据集,其中ChatGPT和GPT-4经常陈述错误的答案,并提供至少一个错误声明的解释。至关重要的是,我们发现ChatGPT和GPT-4可以分别识别67%和87%的错误。我们将这种现象称为幻觉滚雪球:LM过度犯早期错误,导致更多错误,否则就不会犯。
1 引言
2 为什么我们期待幻觉像滚雪球一样越滚越大?
3 实验
4 我们能防止雪球幻觉吗?
5 相关工作
6 结论
我们定义了幻觉滚雪球的现象,并从最先进的模型中证明了它在生成中的普遍性,从而导致了基于简单事实的幻觉,否则这些幻觉是不会发生的。我们的研究结果指出,训练语言模型的风险在于,以牺牲真实性为代价,不加区分地优先考虑流利性和连贯性,我们鼓励未来的工作研究模型开发各个层面的补救措施。
局限性
我们关注的是英语问答中的幻觉滚雪球,而不是在其他任务中探索它,比如摘要或代码生成。
此外,我们只在两个专有模型上进行实验,即ChatGPT和GPT-4,因为它们在许多基准测试上具有最先进的性能。由于这些模型的API的限制,我们无法访问它们输出的概率分布,也无法对它们进行微调。这限制了我们探索潜在缓解策略的能力。访问输出分布将使我们能够使用波束搜索等替代采样方法来研究减轻滚雪球般的幻觉问题。拥有微调模型的能力将使我们能够探索使用不同注释的指令调整是否可以更好地处理我们用来煽动幻觉滚雪球的问题。
相关文章:

How Language Model Hallucinations Can Snowball
本文是LLM系列文章,针对《How Language Model Hallucinations Can Snowball》的翻译。 语言模型幻觉是如何产生雪球的 摘要1 引言2 为什么我们期待幻觉像滚雪球一样越滚越大?3 实验4 我们能防止雪球幻觉吗?5 相关工作6 结论局限性 摘要 在实…...
autojs修改顶部标题栏颜色
顶部标题栏的名字是statusBarColor 不是toolbar。难怪我搜索半天搜不到 修改之后变成这样了 代码如下: "ui"; importClass(android.view.View); importClass(android.graphics.Color); ui.statusBarColor(Color.parseColor("#ffffff")); ui.…...
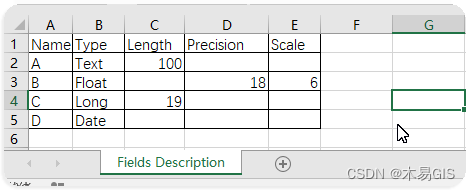
arppy gis 读取text 并批量添加字段 arcpy.AddField_management
arppy gis 读取text 并批量添加字段 arcpy.AddField_management 例:给“省级行政区域”添加“A、B、C、D” 4个字段。 (1)用Excel制作出字段及其描述表,定义字段结构; (2)复制除标题行以为的内…...

Pandas中at、iat函数详解
前言 嗨喽,大家好呀~这里是爱看美女的茜茜呐 at 函数:通过行名和列名来取值(取行名为a, 列名为A的值) iat 函数:通过行号和列号来取值(取第1行,第1列的值) 本文给出at、iat常见的…...
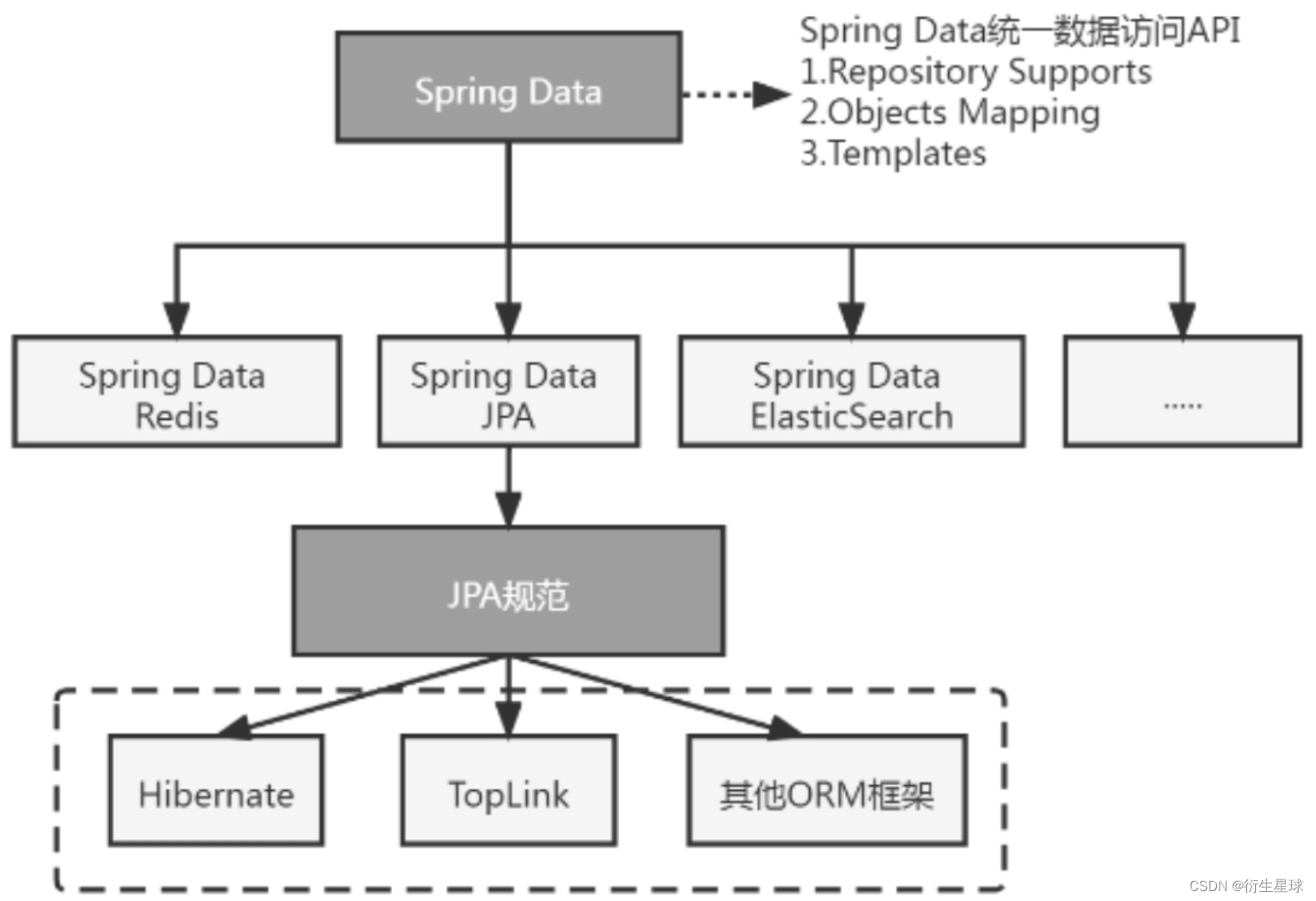
【Spring Boot】JPA — JPA入门
JPA简介 1. JPA是什么 JPA是Sun官方提出的Java持久化规范,它为Java开发人员提供了一种对象/关联映射工具来管理Java应用中的关系数据,通过注解或者XML描述“对象-关系表”之间的映射关系,并将实体对象持久化到数据库中,极大地简…...
)
c#反射(Reflection)
当我们在C#中使用反射时,可以动态地获取和操作程序集、类型和成员。下面是一个简单的C#反射示例,展示了如何使用反射来调用一个类的方法: using System; using System.Reflection;public class MyClass {public void MyMethod(){Console.Wri…...

Lua 元表和元方法
一、元表 元表可以修改一个值在面对一个未知操作时的行为,Lua 中使用 table 作为元表的承载。 元表只能给出预先定义的操作集合的行为,比类会更加受限制,不支持继承。 Lua 每一个值都可以有元表 : 表和用户数据类型都具有各自…...
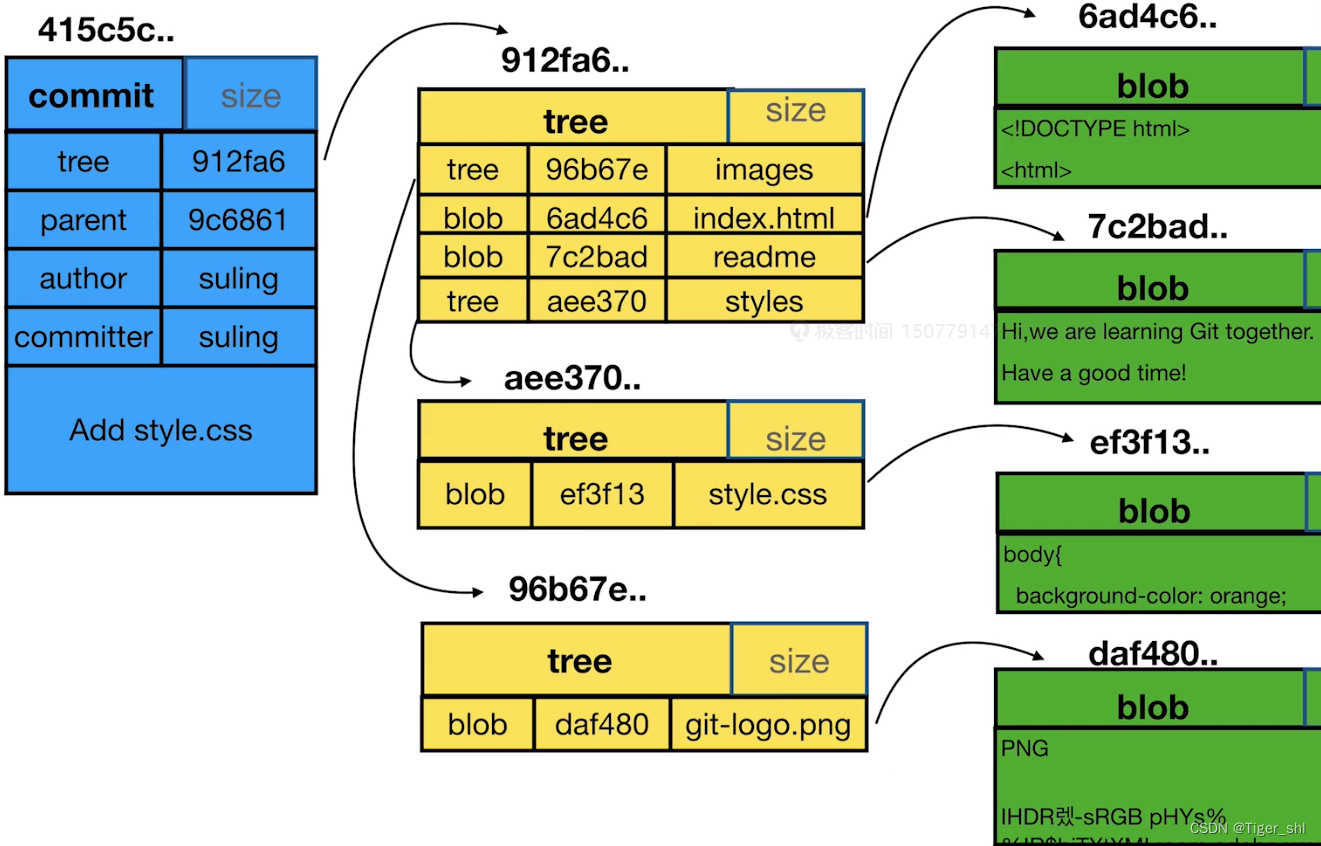
【Git】01-Git基础
文章目录 Git基础1. 简述1.1 版本管理演变1.2 Git的特点 2. Git安装2.1 安装文档2.1 配置user信息 3. 创建仓库3.1 场景3.2 暂存区和工作区 4. 重命名5. 常用git log版本历史5.1 查看当前分支日志5.2 简洁查看日志5.3 查看最近指定条数的日志 6. 通过图形界面工具查看版本7. 探…...

【Vue2.0源码学习】生命周期篇-初始化阶段(initState)
文章目录 1. 前言2. initState函数分析3. 初始化props3.1 规范化数据3.2 initProps函数分析3.3 validateProp函数分析3.4 getPropDefaultValue函数分析3.5 assertProp函数分析 4. 初始化methods5. 初始化data6. 初始化computed6.1 回顾用法6.2 initComputed函数分析6.3 defineC…...

专升本英语零基础学习
1. 词法 1.1 名词 名词(n.),是词类的一种,属于实词。他表示人,物,事,地点或抽象概念的统一名称。 1.1 名词的含义 名词(n.),是词类的一种,属于实词。他表示人&#x…...
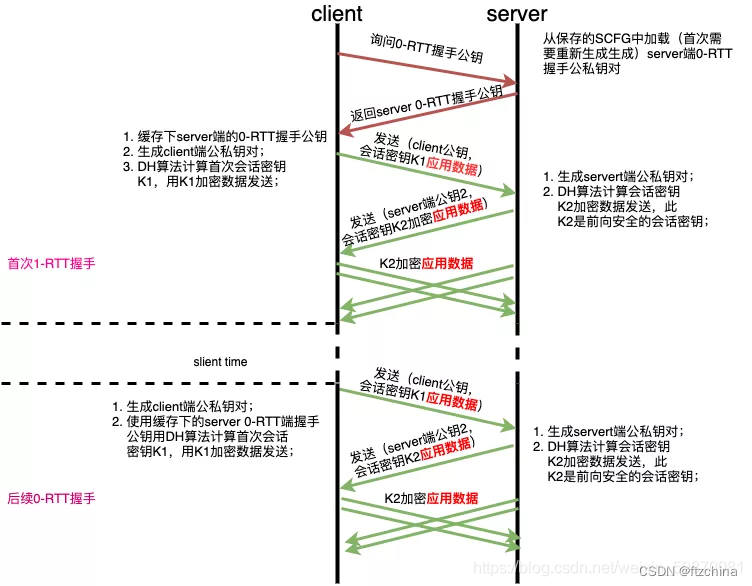
QUIC协议连接详解(二)
目录 一:RTT解释 二:QUIC 1-RTT连接 三:QUIC 0-RTT连接 一:RTT解释 在介绍QUIC协议的连接之前先科普一下什么是RTT。RTT是Round-Trip Time的英文缩写,翻译过来就是一趟来回的时间即往返时延。时间计算即从发送方发送…...

JAVA 经常遇到一些问题【第二部分36~51】
重拾者: 每日记录至目前(记录51种不同场景的问题可参考解决方案) 异常就两部分: 1、excepiton信息: 报错产生的原因 2、at开头表示: 异常产生的代码位置。 欢迎关注本人微信公众号:AIM…...

蓝桥杯打卡Day6
文章目录 N的阶乘基本算术整数查询 一、N的阶乘OI链接 本题思路:本题是关于高精度的模板题。 #pragma GCC optimize(3) #include <bits/stdc.h>constexpr int N1010;std::vector<int> a; std::vector<int> f[N];std::vector<int> mul(in…...

spark集群问题汇总
一、 磁盘问题 问题描述可能原因解决措施core节点磁盘不足, 并且持续增加未开启spark-history的日志清理打开日志清理: spark.history.fs.cleaner.enabled task节点磁盘不足 APP应用使用磁盘过大: 1. 严重的数据倾斜 2. 应用本身数据量大 1. 解决数据倾斜 2. 加大资源, 增加e…...
WebServer 解析HTTP 请求报文
一、TCP 状态转换 浏览器访问网址,TCP传输全过程 二、TCP协议的通信过程 三、TCP 通信流程 // TCP 通信的流程 // 服务器端 (被动接受连接的角色) 1. 创建一个用于监听的套接字- 监听:监听有客户端的连接- 套接字:这…...

Golang开发--interface的使用
在Go语言中,接口(interface)是一种特殊的类型,它定义了一组方法的集合。接口为实现多态性提供了一种机制,允许不同的数据类型实现相同的方法,从而可以以统一的方式处理这些不同类型的对象。接口在Go中广泛用…...
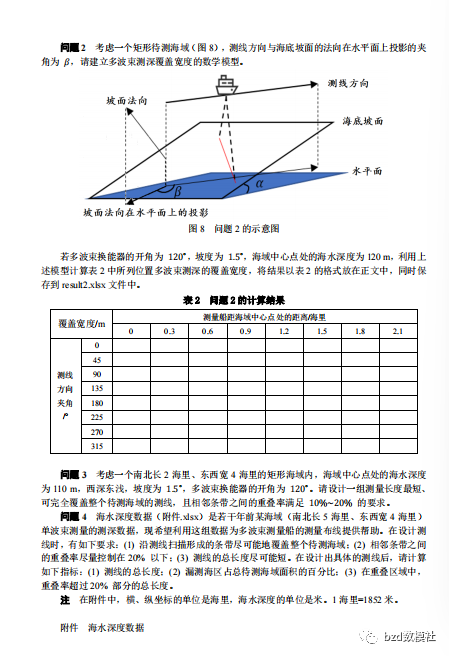
2023 年高教社杯全国大学生数学建模竞赛题目 B 题 多波束测线问题
B 题 多波束测线问题 单波束测深是利用声波在水中的传播特性来测量水体深度的技术。声波在均匀介质中作匀速直线传播,在不同界面上产生反射,利用这一原理,从测量船换能器垂直向海底发射声波信号,并记录从声波发射到信号接收的传播…...

leetcode算法题--生成特殊数字的最少操作
原题链接:https://leetcode.cn/problems/minimum-operations-to-make-a-special-number/description/ 感觉还是比较难想到的。。 func minimumOperations(num string) int {res : len(num)if strings.Contains(num, "0") {res-- }f : func(tail string)…...

数学建模--决策树的预测模型的Python实现
目录 1.算法流程简介 2.算法核心代码 3.算法效果展示 1.算法流程简介 """ 决策树的应用:对泰坦尼克号数据集成员进行预测生死 算法流程还是比较简单的,简单学习一下决策树跟着注释写即可 文章参考:https://zhuanlan.zhihu.com/p/133838427 算法种遇上sklear…...

Linkstech多核并行仿真丨光伏发电系统模型及IEEE 39 bus模型多核并行实测
新能源场站和区域电网作为复杂且具有动态特性的大规模电力系统,需要实时仿真测试来验证其性能、稳定性和响应能力。在这种背景下,多核并行仿真运算显得尤为重要。多核并行仿真能够同时处理电力系统的复杂模型,加速仿真过程,实现接…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
