OpenCV(二十五):边缘检测(一)
目录
1.边缘检测原理
2.Sobel算子边缘检测
3.Scharr算子边缘检测
4.两种算子的生成getDerivKernels()
1.边缘检测原理
其原理是基于图像中灰度值的变化来捕捉图像中的边界和轮廓。梯度则表示了图像中像素强度变化的强弱和方向。 所以沿梯度方向找到有最大梯度值的像素,就可以获得图像中的边缘信息。

2.Sobel算子边缘检测
原理:
Sobel算子是一种常用的边缘检测算子,它可以通过计算图像的梯度来捕捉图像中的边缘信息。它分别计算图像在x和y方向上的导数,然后根据导数的值确定边缘的位置和强度。
具体来说,Sobel算子可以通过一个3x3的卷积核在图像上进行卷积操作。有两个Sobel卷积核,一个用于水平方向(x方向)的边缘检测,另一个用于垂直方向(y方向)的边缘检测。这两个卷积核分别如下:

对于输入图像中的每个像素,Sobel算子将使用这些卷积核计算其水平和垂直方向上的梯度。然后,通过对梯度的幅度进行合并,可以计算出每个像素的总梯度大小。总梯度大小表示像素点周围灰度值的变化强度,较大的变化强度通常对应于图像中的边缘。
函数:
cv::Sobel()函数将Sobel算子应用于输入图像进行卷积操作。
函数的原型如下:
CV_EXPORTS_W void Sobel( InputArray src, OutputArray dst, int ddepth,
int dx, int dy, int ksize = 3,
double scale = 1, double delta = 0,
int borderType = BORDER_DEFAULT );
下面是参数的详细解释:
-
src:输入图像,可以是单通道灰度图像或多通道图像。
-
dst:输出图像,与输入图像具有相同的尺寸和类型。
-
ddepth:输出图像的数据类型,它可以是负值(如-1)表示与输入图像保持一致,也可以是CV_8U、CV_16U、CV_32F等值,表示输出图像的深度。
-
dx和dy:分别表示在x和y方向上的导数阶数。可选值为0、1和2。
-
ksize:Sobel内核的大小,必须为1、3、5或7。值越大,滤波器的响应越平缓。
-
scale:可选的缩放因子,用于调整输出图像的值域范围。默认为1。
-
delta:可选的指定delta值,用于调整输出图像的亮度。默认为0。
-
borderType:可选的边界扩充方法,用于处理邻域超出图像边界的情况。默认为cv::BORDER_DEFAULT。
示例代码:
void Sobel_f(Mat image){Mat gray;cvtColor(image,gray,COLOR_BGR2GRAY);Mat resultX,resultY,resultXY;//X方向一阶边缘Sobel(gray,resultX,CV_16S,1,0,1);convertScaleAbs(resultX,resultX);//Y方向一阶边缘Sobel(gray,resultY,CV_16S,0,1,3);convertScaleAbs(resultY,resultY);//整幅图像的一阶边缘resultXY=resultX+resultY;//显示图像imwrite("/sdcard/DCIM/resultX.png",resultX);imwrite("/sdcard/DCIM/resultY.png",resultY);imwrite("/sdcard/DCIM/resultXY.png",resultXY);}


(X方向) ( Y方向) ( XY方向)
3.Scharr算子边缘检测
原理:
Scharr算子是一种边缘检测算子,它是Sobel算子的改进版本。Scharr算子采用了更加精确的权重分配,可以提供更好的边缘检测性能。
Scharr算子也是通过卷积操作来计算图像的梯度,类似于Sobel算子。它包含两个卷积核,一个用于水平方向(x方向)的边缘检测,另一个用于垂直方向(y方向)的边缘检测。

Scharr算子的差异在于卷积核中的权重分配相对于Sobel算子更加平衡,以提高对边缘信号的敏感度。这种平衡权重的分配可以产生更加准确的梯度估计。
Scharr算子使用相同的原理来计算像素点周围的梯度大小和方向。通过在x和y方向上对梯度进行计算,并根据梯度的幅度和方向确定边缘的位置和强度。
函数:
cv::Scharr()函数是OpenCV中的一个函数,用于计算图像的Scharr导数。它类似于Sobel算子,但是使用了更准确的权重分配。
函数原型:
CV_EXPORTS_W void Scharr( InputArray src, OutputArray dst, int ddepth,
int dx, int dy, double scale = 1, double delta = 0,
int borderType = BORDER_DEFAULT );
下面是参数的详细解释:
-
src:输入图像,可以是单通道灰度图像或多通道图像。
-
dst:输出图像,与输入图像具有相同的尺寸和类型。
-
ddepth:输出图像的数据类型,可以是负值(如-1),表示与输入图像保持一致,也可以是CV_8U、CV_16U、CV_32F等值,表示输出图像的深度。
-
dx和dy:分别表示在x和y方向上的导数阶数。可选值为0、1和2。
-
scale:可选的缩放因子,用于调整输出图像的值域范围。默认为1。
-
delta:可选的指定delta值,用于调整输出图像的亮度。默认为0。
-
borderType:可选的边界扩充方法,用于处理邻域超出图像边界的情况。默认为cv::BORDER_DEFAULT。
示例代码:
void Scharr_f(Mat img) {Mat image;cvtColor(img,image,COLOR_BGR2GRAY);cv::Mat grad_x, grad_y; // 存放Scharr滤波器的梯度cv::Mat abs_grad_x, abs_grad_y; // 存放梯度的绝对值// 计算X方向的Scharr滤波器cv::Scharr(image, grad_x, CV_16S, 1, 0);cv::convertScaleAbs(grad_x, abs_grad_x);// 计算Y方向的Scharr滤波器cv::Scharr(image, grad_y, CV_16S, 0, 1);cv::convertScaleAbs(grad_y, abs_grad_y);// 合并X和Y方向的梯度cv::Mat grad;cv::addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad);// 显示结果imwrite("/sdcard/DCIM/grad.png",grad);
}
结果: (grad)
(grad)
4.两种算子的生成getDerivKernels()
getDerivKernels()函数是OpenCV中用于生成一维卷积核的函数,可用于计算图像的一阶导数。
函数的原型如下:
void cv::getDerivKernels ( OutputArray kx,
OutputArray ky,
int dx,
int dy,
int ksize,
bool normalize =false,
int ktype = CV_32F
)
- kx:行滤波器系数的输出矩阵,尺寸为ksize*1
- ky:列滤波器系数的输出矩阵,尺寸为ksize*1。
- dx:X方向导数的阶次。
- dy:Y方向导数的阶次
- ksize:滤波器的大小,可以选择的参数为FILTER SCHARR,1.35或7。
- normalize: 是否对滤波器系数进行归一化的标志,默认值为false,表示不进行系数归一化。
- ktype:滤波器系数类型,可以选择CV 32F或CV 64F,默认参数为CV 32F。
示例代码:
以下是一个使用使用getDerivKernels()函数来生成Sobel和Scharr算子卷积核的示例:
//生成边缘检测器
void f(){cv::Mat sobel_xl, sobel_yl; // 存放分离的Sobel算子cv::Mat scharr_x, scharr_y; // 存放分离的Scharr算子cv::Mat sobelXl, scharrX; // 存放最终算子// 一阶X方向Sobel算子cv::getDerivKernels(sobel_xl, sobel_yl, 1, 0, 3);sobel_xl = sobel_xl.reshape(1, 1); // 转换为单行矩阵sobelXl = sobel_yl * sobel_xl; // 计算滤波器// X方向Scharr算子cv::getDerivKernels(scharr_x, scharr_y, 1, 0, cv::FILTER_SCHARR);scharr_x = scharr_x.reshape(1, 1); // 转换为单行矩阵scharrX = scharr_y*scharr_x; // 计算滤波器ostringstream ss;// 打印生成的卷积核ss<< "Sobel X方向卷积核:" << sobelXl << endl;ss << "Scharr X方向卷积核:" << scharrX <<endl;LOGD("%s",ss.str().c_str());
}我们使用getDerivKernels()函数生成了X方向Sobel算子和X方向Scharr算子的卷积核。然后,我们将其转换为单行矩阵,并通过乘法运算计算得到滤波器。
相关文章:

OpenCV(二十五):边缘检测(一)
目录 1.边缘检测原理 2.Sobel算子边缘检测 3.Scharr算子边缘检测 4.两种算子的生成getDerivKernels() 1.边缘检测原理 其原理是基于图像中灰度值的变化来捕捉图像中的边界和轮廓。梯度则表示了图像中像素强度变化的强弱和方向。 所以沿梯度方向找到有最大梯度值的像素&…...

上行取消指示 DCI format 2_4
上篇介绍了DCI format 2_1的DL传输中断的内容,这篇就看下DCI format 2_4有关的UL 传输取消机制,值得注意的是这里的UL传输针对的是PUSCH和SRS传输。 UL cancellation DCI format 2_4相关机制引入的背景与DCI format 2_1一样,都是因为URLLC和e…...
百望云蝉联2023「Cloud 100 China 」榜单 综合实力再获认可
9月7日,2023 Cloud 100 China 榜单于上海中心正式发布,榜单由靖亚资本与崔牛会联合推出,百望云凭借着过硬的综合实力与卓越的技术创新能力,再次荣登榜单,位居第六位。 本届评选,Top 100 企业的数据指标的权…...

力扣刷题班第1节:Python语法常遗漏的知识
以下仅仅记录和后面力扣刷题相关的、且平常会遗漏的语法知识。 下面这些笔记都是点到为止,不进行深入解释。大多数学过python的朋友看到就知道什么意思的,我就不解释了 字符串 str "I am a cook"# 按照空格切分 str.split(" ") …...

GET 和 POST请求的区别是什么
GET和POST是HTTP请求的两种基本方法,要说它们的区别,接触过WEB开发的人都能说出一二。 最直观的区别就是GET把参数包含在URL中,POST通过request body传递参数。 你轻轻松松的给出了一个“标准答案”: GET在浏览器回退时是无害的…...
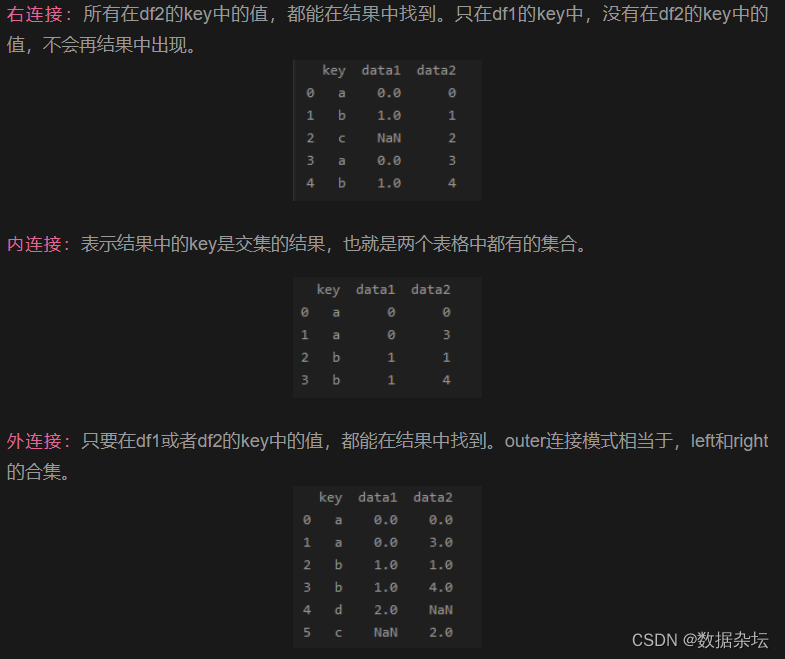
Python数据分析实战-表连接-merge四种连接方式用法(附源码和实现效果)
实现功能 表连接-merge四种连接方式用法, 将两个pandas表根据一个或者多个键(列)值进行连接。 实现代码 import pandas as pddf1 pd.DataFrame({key: [a, b, d],data1: range(3)}) print(df1)df2 pd.DataFrame({key: [a, b, c, a, b],dat…...

NFTScan 浏览器再升级:优质数据服务新体验来袭
当前,高质量的 NFT 数据服务已成为区块链用户和开发者的必需。为满足用户数据需求,NFTScan 主站近日进行全面升级,优化了数据服务板块的页面结构,实现更清晰简洁的布局和交互。 NFTScan 的改版充分考虑用户和开发者的数据体验&am…...
C# 去除utf-8 BOM头
static void Main(string[] args) {var a1 Encoding.UTF8.GetBytes("<");var a2 Encoding.UTF8.GetBytes("<");Console.WriteLine("去除utf-8 bom之前");Console.WriteLine(Encoding.UTF8.GetString(a1));Console.WriteLine(…...

Java注解以及自定义注解
Java注解以及自定义注解 要深入学习注解,我们就必须能定义自己的注解,并使用注解,在定义自己的注解之前,我们就必须要了解Java为 我们提供的元注解和相关定义注解的语法。 1、注解 1.1 注解的官方定义 注解是一种元数据形式。…...
[开学季]ChatPaper全流程教程
文章目录 1. 粗筛:论文全文总结1.1 使用步骤: 1.2 功能描述:2. 论文问答:2. 精读:学术版GPT的论文翻译2.0 论文精读的正确姿势2.1 使用场景1:arxiv论文完美翻译2.2 本地PDF全文翻译:2.3 关于免费…...

Spring学习笔记——4
Spring学习笔记——4 一、基于AOP的声明式事务控制1.1、Spring事务编程概述1.2、搭建测试环境1.3、基于XML声明式事务控制1.4、基于注解声明式事务控制 二、Spring整合web环境2.1、JavaWeb三大组件作用及其特点2.2、Spring整合web环境的思路及实现2.3、Spring的Web开发组件spri…...

Python数据科学入门
推荐:使用 NSDT场景编辑器 快速搭建3D应用场景 来自不同角色的人都希望保住自己的工作,因此他们将致力于发展自己的技能以适应当前的市场。这是一个竞争激烈的市场,我们看到越来越多的人对数据科学产生兴趣;该行业有数千门在线课程、训练营和…...

Ubuntu 22.04 编译 DPDK 19.11 igb_uio 和 kni 报错解决办法
由于 Ubuntu22.04 内核版本和gcc版本比较高,在编译dpdk时会报错。 我使用的编译命令是: make install Tx86_64-native-linuxapp-gcc主要有以下几个错误: 1.error: this statement may fall through Build kernel/linux/igb_uioCC [M] /roo…...

Android Studio.exe 下载 2023 最新更新,网盘下载
方便大家下载, 放到了网盘上,自己也保留一份。(最前面是最新版本的,慎用, 会有bug什么的) 个人使用4.2版本的,感觉够用稳定,其他版本有莫名奇妙的bug,让人头大࿰…...
element的el-select给下拉框添加背景
第一步 :popper-append-to-body"false" <el-selectv-model"value"placeholder"请选择":popper-append-to-body"false"><el-optionv-for"item in options":key"item.value":label"item.label&quo…...

正确理解党籍和党龄;入党和转正时间
总的来说党籍、党龄、入党时间、转正时间在性质和时间阶段上均有所区别。 党籍:是指党员资格。经支部党员大会讨论,被批准为预备党员之日起,就有了党籍。若被取消预备党员资格、劝退除名、自行脱党、开除党籍的,就失去了党籍。 …...

C语言基础:printf 函数介绍;以及常用四种常用的数据类型
printf 函数介绍 #include <stdio.h> int main() { /* * %c:字符 ; %d:带符号整数; %f: 浮点数; %s: 一串字符; */ int age21; printf(“hello %s,you are %d years old\n”,“Bob”,age); int i 10; double f96.20; printf(“student number%3d,score%f\n”…...
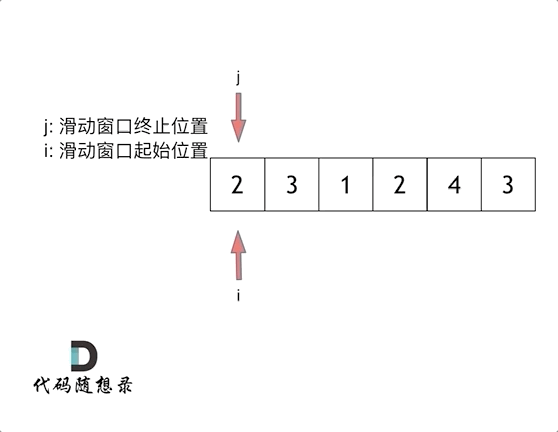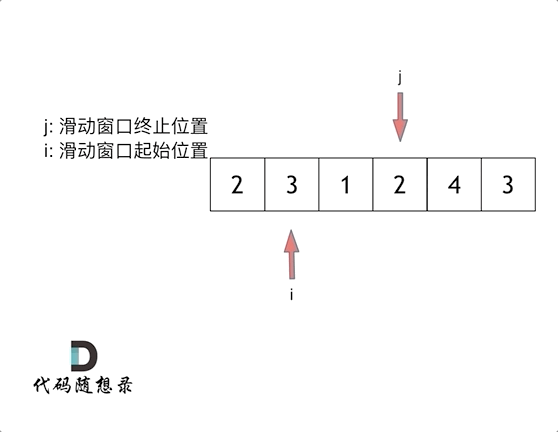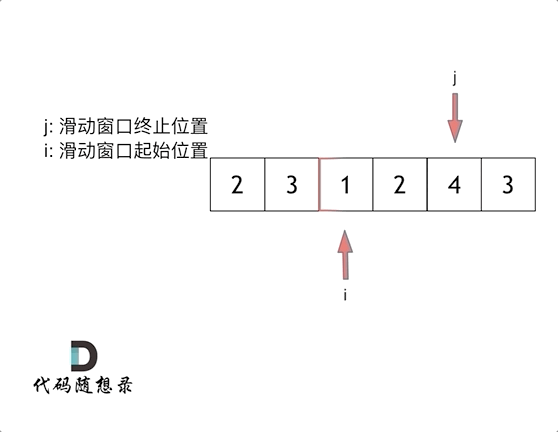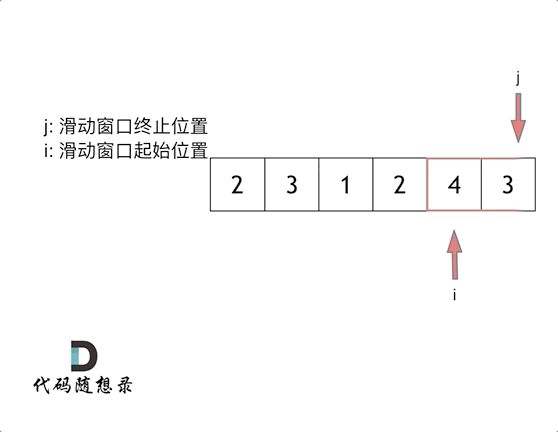
【LeetCode-中等题】209. 长度最小的子数组
文章目录 题目方法一:滑动窗口:方法二: 题目 方法一:滑动窗口: 参考图解动画:长度最小的子数组 class Solution { //方法一:滑动窗口public int minSubArrayLen(int target, int[] nums) {int n nums.l…...
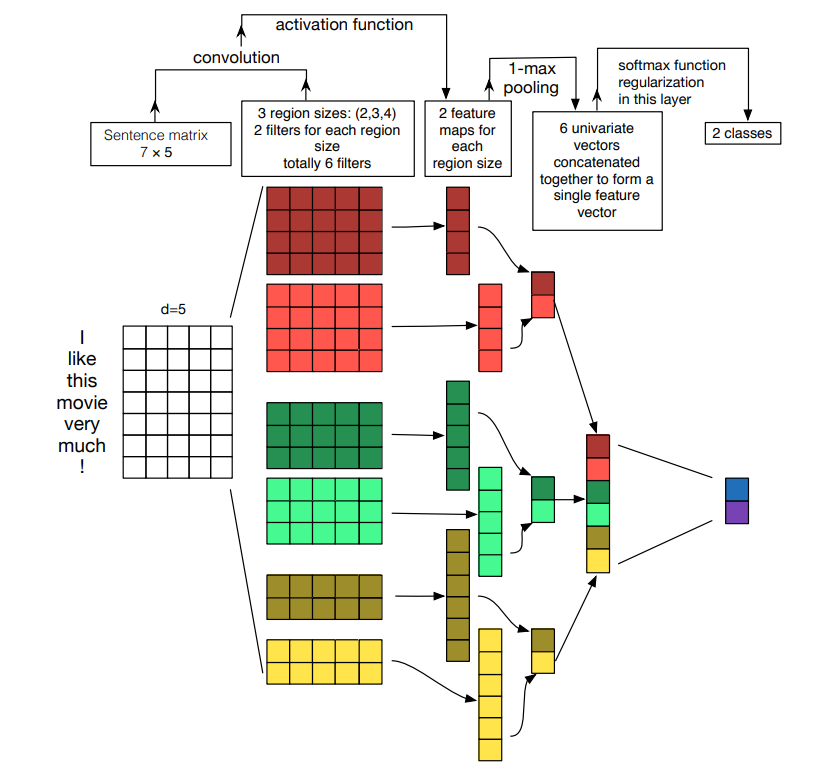
比较聚合模型实战文本匹配
引言 本文我们采用比较聚合模型来实现文本匹配任务。 数据准备 数据准备包括 构建词表(Vocabulary)构建数据集(Dataset) 本次用的是LCQMC通用领域问题匹配数据集,它已经分好了训练、验证和测试集。 我们通过pandas来加载一下。 import pandas as pdtrain_df …...

LA@二次型@标准化相关原理和方法
文章目录 标准化方法正交变换法🎈求矩阵的特征值求各特征值对应的线性无关特征向量组正交化各个向量组 配方法步骤例例 初等变换法原理总结初等变换法的步骤例 标准化方法 正交变换法🎈 二次型可标准化定理的证明过程给出使用二次型标准化的步骤 该方法…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...
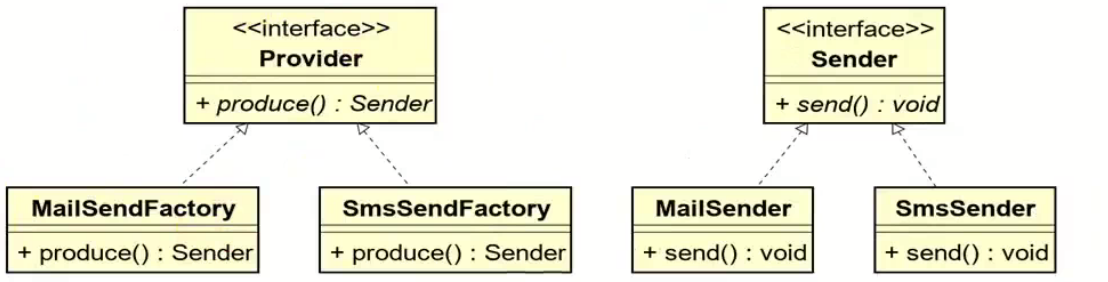
工厂方法模式和抽象工厂方法模式的battle
1.案例直接上手 在这个案例里面,我们会实现这个普通的工厂方法,并且对比这个普通工厂方法和我们直接创建对象的差别在哪里,为什么需要一个工厂: 下面的这个是我们的这个案例里面涉及到的接口和对应的实现类: 两个发…...
