LA@二次型@标准化相关原理和方法
文章目录
- 标准化方法
- 正交变换法🎈
- 求矩阵的特征值
- 求各特征值对应的线性无关特征向量组
- 正交化各个向量组
- 配方法
- 步骤
- 例
- 例
- 初等变换法
- 原理
- 总结初等变换法的步骤
- 例
标准化方法
正交变换法🎈
-
二次型可标准化定理的证明过程给出使用二次型标准化的步骤
-
该方法通过计算出一个特定的正交矩阵 P \bold P P,并用 P \bold P P来进行线性变换实现得到标准形
求矩阵的特征值
-
求出 n n n元二次型矩阵 A \bold A A的全部特征值 λ i \lambda_i λi,它们分别是 n i n_i ni重根(而且对应 n i n_i ni个线性无关的特征向量)
- ∑ i s n i = n \sum_{i}^{s}n_i=n ∑isni=n, i = 1 , 2 , ⋯ , s i=1,2,\cdots,s i=1,2,⋯,s(表示A有s个互异的特征根)
求各特征值对应的线性无关特征向量组
-
对每个 λ i \lambda_i λi求出对应的齐次线性方程组 ( λ i E − A ) x = 0 \bold{(\lambda_i{E}-A)x=0} (λiE−A)x=0的基础解系 Φ i \Phi_i Φi(包含 n i n_i ni个线性无关向量)
- Φ i : α 1 ( i ) , ⋯ , α n i ( i ) \Phi_{i}:\alpha_1^{(i)},\cdots,\alpha_{n_i}^{(i)} Φi:α1(i),⋯,αni(i), i i i表示向量(组)属于特征值 λ i \lambda_i λi,包含 n i n_i ni个线性无关的向量
正交化各个向量组
-
分别对 Φ 1 , ⋯ , Φ s \Phi_1,\cdots,\Phi_{s} Φ1,⋯,Φs正交化得到向量组 Ψ = ϕ 1 , ⋯ , ϕ s \Psi=\phi_1,\cdots,\phi_{s} Ψ=ϕ1,⋯,ϕs( ϕ i 是 Φ i \phi_i是\Phi_i ϕi是Φi正交化后的向量组)
-
令矩阵 P = ( Ψ ) \bold P=(\Psi) P=(Ψ),则 P \bold P P能使 P T A P = Λ \bold{P^{T}AP=\Lambda} PTAP=Λ= diag ( λ i , ⋯ , λ n ) \text{diag}(\lambda_i,\cdots,\lambda_n) diag(λi,⋯,λn)
-
则正交线性变换 x = P y \bold{x=Py} x=Py就是所求的线性变换
-
y = ( y 1 , ⋯ , y n ) T \bold y=(y_1,\cdots,y_n)^{T} y=(y1,⋯,yn)T
-
f ( x 1 , ⋯ , x n ) → x = Q y g ( y 1 , ⋯ , y n ) = ∑ i = 1 n λ i y i 2 f(x_1,\cdots,x_n)\xrightarrow{x=Qy}g(y_1,\cdots,y_n)=\sum\limits_{i=1}^{n}\lambda_iy_i^2 f(x1,⋯,xn)x=Qyg(y1,⋯,yn)=i=1∑nλiyi2
-
配方法
- 用正交变换化二次型成标准形,具有保持几何形状不变的优点
- 如果不局限于用正交变换,还可以有多种方法确定一个一般的可逆矩阵来标准化二次型
- 例如拉格朗日配方法,其原理和依据参见二次型可标准化定理的配方角度证明过程
步骤
- 若 f ( x 1 , ⋯ , x 2 ) = ∑ i = 2 n ∑ j = 2 n a i j x i x j f(x_1,\cdots,x_2)=\sum_{i=2}^{n}\sum_{j=2}^{n}a_{ij}x_ix_j f(x1,⋯,x2)=∑i=2n∑j=2naijxixj, a j i = a i j a_{ji}=a_{ij} aji=aij包含 x i x_i xi的平方项(设为 a i i x i 2 a_{ii}x_i^2 aiixi2),那么将 x i x_i xi相关的项集中求和,记为 u i = ∑ j ≠ i n 2 a i j x i x j u_i=\sum_{j\neq{i}}^{n}2a_{ij}x_{i}x_{j} ui=∑j=in2aijxixj;对 η i = a i i x i 2 + u i \eta_i=a_{ii}x_i^2+u_i ηi=aiixi2+ui进行配方,得到形如 η i = b i ( x i + ⋯ ) 2 + ⋯ \eta_{i}=b_{i}(x_{i}+\cdots)^{2}+\cdots ηi=bi(xi+⋯)2+⋯,从而 f = η i + v i f=\eta_i+v_i f=ηi+vi= b i ( x i i + ⋯ ) 2 + ⋯ + v i b_{i}(x_{ii}+\cdots)^{2}+\cdots+v_i bi(xii+⋯)2+⋯+vi
(1),- 其中 v i = f − η i = ∑ r , j ≠ i a r j x r x j v_i=f-\eta_i=\sum_{r,j\neq{i}}a_{rj}x_rx_j vi=f−ηi=∑r,j=iarjxrxj
- 易知,
(1)式中只有第一项 b i ( x i + ⋯ ) 2 b_{i}(x_{i}+\cdots)^{2} bi(xi+⋯)2包含 x i i x_{ii} xii,其余项不包含 x i i x_{ii} xii - 不断地对
(1)中的下一个平方项进行配方(理论分析中已经指出,(1)包含了所有 x i x_i xi的平方项 i = 1 , ⋯ , n i=1,\cdots,n i=1,⋯,n,最终所有 x i , i = 1 , ⋯ , n x_i,i=1,\cdots,n xi,i=1,⋯,n都会被配方成形如 b i ( x i i + ⋯ ) 2 b_{i}(x_{ii}+\cdots)^2 bi(xii+⋯)2的形式 - 构造线性变换: y i = x i + ⋯ y_i=x_{i}+\cdots yi=xi+⋯,
(2)( i = 1 , ⋯ , n ) (i=1,\cdots,n) (i=1,⋯,n);求解该线性方程组,得到线性变换 x i = y i − ⋯ x_i=y_i-\cdots xi=yi−⋯(3) - 那么线性变换
(3)就能够使 f f f标准化
- 若 f f f中不包含任意平方项,但是包含某个 a i j ≠ 0 a_{ij}\neq{0} aij=0, i ≠ j i\neq{j} i=j则运用线性变换
- x i = y i − y j x_i=y_{i}-y_{j} xi=yi−yj
- x j = y i + y j x_j=y_i+y_j xj=yi+yj
- x k = y k x_k=y_k xk=yk, k = 1 , ⋯ , n k=1,\cdots,n k=1,⋯,n且 k ≠ i , j k\neq{i,j} k=i,j
- 代入该线性变换到 f f f可以将此类情况转换为第一种情况(包含平方项)求解
例
-
f ( x 1 , x 2 , x 3 ) = 4 ( x 1 2 + x 2 2 + x 3 + x 1 x 2 + x 1 x 3 + x 2 x 3 ) f(x_1,x_2,x_3)=4(x_1^2+x_2^2+x^3+x_1x_2+x_1x_3+x_2x_3) f(x1,x2,x3)=4(x12+x22+x3+x1x2+x1x3+x2x3)
-
配方得到
(0)
f ( x 1 , x 2 , x 3 ) = 4 ( x 1 2 + x 1 ( x 2 + x 3 ) + x 2 2 + x 3 2 + x 2 x 3 ) = 4 [ ( x 1 + 1 2 x 1 ( x 2 + x 3 ) ) 2 − 1 4 ( x 2 + x 3 ) 2 + x 2 2 + x 3 2 + x 2 x 3 ] = 4 ( x 1 + 1 2 ( x 2 + x 3 ) ) 2 − ( x 2 2 + 2 x 2 x 3 + x 3 2 ) + 4 ( x 2 2 + x 3 2 + x 2 x 3 ) = 4 ( x 1 + 1 2 ( x 2 + x 3 ) ) 2 + 3 x 2 2 + 3 x 3 2 + 2 x 2 x 3 = 4 ( x 1 + 1 2 ( x 2 + x 3 ) ) 2 + 3 ( x 2 2 + 2 3 x 2 x 3 ) + 3 x 3 2 = 4 ( x 1 + 1 2 ( x 2 + x 3 ) ) 2 + 3 [ ( x 2 + 1 3 x 3 ) 2 − 1 9 x 3 2 ] + 3 x 3 2 = 4 ( x 1 + 1 2 ( x 2 + x 3 ) ) 2 + 3 ( x 2 + 1 3 x 3 ) 2 − 1 3 x 3 2 + 3 x 3 2 = 4 ( x 1 + 1 2 ( x 2 + x 3 ) ) 2 + 3 ( x 2 + 1 3 x 3 ) 2 + 8 3 x 3 2 \begin{aligned} f(x_1,x_2,x_3) &=4(x_1^2+x_1(x_2+x_3)+x_2^2+x_3^2+x_2x_3) \\&=4[(x_1+\frac{1}{2}x_1(x_2+x_3))^2-\frac{1}{4}(x_2+x_3)^2+x_2^2+x_3^2+x_2x_3] \\&=4(x_1+\frac{1}{2}(x_2+x_3))^2-(x_2^2+2x_2x_3+x_3^2)+4(x_2^2+x_3^2+x_2x_3) \\&=4(x_1+\frac{1}{2}(x_2+x_3))^2+3x_2^2+3x_3^2+2x_2x_3 \\&=4(x_1+\frac{1}{2}(x_2+x_3))^2+3(x_2^2+\frac{2}{3}x_2x_3)+3x_3^2 \\&=4(x_1+\frac{1}{2}(x_2+x_3))^2+3[(x_2+\frac{1}{3}x_3)^2-\frac{1}{9}x_3^2]+3x_3^2 \\&=4(x_1+\frac{1}{2}(x_2+x_3))^2+3(x_2+\frac{1}{3}x_3)^2-\frac{1}{3}x_3^2+3x_3^2 \\&=4(x_1+\frac{1}{2}(x_2+x_3))^2+3(x_2+\frac{1}{3}x_3)^2+\frac{8}{3}x_3^2 \end{aligned} f(x1,x2,x3)=4(x12+x1(x2+x3)+x22+x32+x2x3)=4[(x1+21x1(x2+x3))2−41(x2+x3)2+x22+x32+x2x3]=4(x1+21(x2+x3))2−(x22+2x2x3+x32)+4(x22+x32+x2x3)=4(x1+21(x2+x3))2+3x22+3x32+2x2x3=4(x1+21(x2+x3))2+3(x22+32x2x3)+3x32=4(x1+21(x2+x3))2+3[(x2+31x3)2−91x32]+3x32=4(x1+21(x2+x3))2+3(x2+31x3)2−31x32+3x32=4(x1+21(x2+x3))2+3(x2+31x3)2+38x32 -
令 { y 1 = x 1 + 1 2 ( x 2 + x 3 ) y 2 = x 2 + 1 3 x 3 y 3 = x 3 \begin{cases}y_1=&x_1+\frac{1}{2}(x_2+x_3)\\y_2=&x_2+\frac{1}{3}x_3\\y_3=&x_3\end{cases} ⎩ ⎨ ⎧y1=y2=y3=x1+21(x2+x3)x2+31x3x3
(1);则 f ( x 1 , x 2 , x 3 ) = g ( y 1 , y 2 , y 3 ) = 4 y 1 2 + 3 y 2 2 + 8 3 y 3 2 f(x_1,x_2,x_3)=g(y_1,y_2,y_3)=4y_1^2+3y_2^2+\frac{8}{3}y_3^2 f(x1,x2,x3)=g(y1,y2,y3)=4y12+3y22+38y32,这是一个标准形二次型 -
通过解线性方程组
(1),得 y → x \bold{y\to{x}} y→x所用的线性变换 x = Q y \bold{x=Qy} x=Qy-
x 1 = y 1 − 1 2 y 2 − 1 3 y 3 x_1=y_1-\frac{1}{2}y_2-\frac{1}{3}y_3 x1=y1−21y2−31y3
-
x 2 = y 2 − 1 3 y 3 x_2=y_2-\frac{1}{3}y_3 x2=y2−31y3
-
x 3 = y 3 x_3=y_3 x3=y3
-
变换矩阵: Q = ( 1 − 1 2 − 1 3 0 1 − 1 3 0 0 1 ) \bold Q=\begin{pmatrix}1&-\frac{1}{2}&-\frac{1}{3}\\0&1&-\frac{1}{3}\\0&0&1\end{pmatrix} Q= 100−2110−31−311
-
求变换矩阵也可利用可逆线性变换的逆变换公式:若 y = C x \bold{y=Cx} y=Cx则 x = C − 1 y \bold{x=C^{-1}y} x=C−1y,也是计算 C = ( 1 1 2 1 2 0 1 1 3 0 0 1 ) \bold C=\begin{pmatrix}1&\frac{1}{2}&\frac{1}{2}\\0&1&\frac{1}{3}\\0&0&1\end{pmatrix} C= 100211021311 的逆矩阵 C \bold{C} C,则 Q = C − 1 \bold{Q=C^{-1}} Q=C−1
-
将此线性变换代入 f f f或者 g g g中就可得到 f f f的标准形: f = 4 y 1 2 + 3 y 2 2 + 8 3 y 3 2 f=4y_1^2+3y_2^2+\frac{8}{3}y_3^2 f=4y12+3y22+38y32,这个表达式可以从已经配好方的式
(2)中直接读出(将平方项依次用 y 1 , ⋯ , y n y_1,\cdots,y_n y1,⋯,yn代替)
-
例
-
f ( x 1 , x 2 , x 3 ) = x 1 x 2 + x 1 x 3 + 2 x 2 x 3 f(x_1,x_2,x_3)=x_1x_2+x_1x_3+2x_2x_3 f(x1,x2,x3)=x1x2+x1x3+2x2x3标准化
-
对于 x 1 x 2 x_1x_2 x1x2
-
T : { x 1 = y 1 − y 2 x 2 = y 1 + y 2 x 3 = y 3 T = ( 1 1 0 1 − 1 0 0 0 1 ) T:\begin{cases} x_1=y_1-y_2\\ x_2=y_1+y_2\\ x_3=y_3 \end{cases} \\ T=\begin{pmatrix} 1&1&0\\ 1&-1&0\\ 0&0&1 \end{pmatrix} T:⎩ ⎨ ⎧x1=y1−y2x2=y1+y2x3=y3T= 1101−10001
-
把线性变换 x = T y \bold{x=Ty} x=Ty带入 f f f;
- f = ( y 1 − y 2 ) ( y 1 + y 2 ) + ( y 1 − y 2 ) y 3 + 2 ( y 1 + y 2 ) ( y 3 ) = y 1 2 − y 2 2 + y 1 y 3 − y 2 y 3 + 2 y 1 y 3 + 2 y 2 y 3 = y 1 2 − y 2 2 + 3 y 1 y 3 + y 2 y 3 f=(y_1-y_2)(y_1+y_2)+(y_1-y_2)y_3+2(y_1+y_2)(y_3) \\=y_1^2-y_2^2+y_1y_3-y_2y_3+2y_1y_3+2y_2y_3 \\=y_1^2-y_2^2+3y_1y_3+y_2y_3 f=(y1−y2)(y1+y2)+(y1−y2)y3+2(y1+y2)(y3)=y12−y22+y1y3−y2y3+2y1y3+2y2y3=y12−y22+3y1y3+y2y3
-
问题转换为第一种类型,配方得:式
(1)- g ( y 1 , y 2 , y 3 ) = ( y 1 + 3 2 y 3 ) 2 − ( y 2 + 1 2 y 3 ) 2 − 2 y 3 2 g(y_1,y_2,y_3)=(y_1+\frac{3}{2}y_3)^2-(y_2+\frac{1}{2}y_3)^2-2y_3^2 g(y1,y2,y3)=(y1+23y3)2−(y2+21y3)2−2y32
-
令
{ z 1 = y 1 + 3 2 y 3 z 2 = y 1 + 1 2 y 3 z 3 = y 3 f = z 1 2 − z 2 2 − 2 z 3 2 \\ \begin{cases} z_1=y_1+\frac{3}{2}y_3\\ z_2=y_1+\frac{1}{2}y_3\\ z_3=y_3 \end{cases} \\ f=z_1^2-z_2^2-2z_3^2 ⎩ ⎨ ⎧z1=y1+23y3z2=y1+21y3z3=y3f=z12−z22−2z32 -
解上述线性方程组,得新线性变换 y = Q z \bold{y=Qz} y=Qz及其变换矩阵:
{ y 1 = z 1 − 3 2 z 3 y 2 = z 2 − 1 2 z 3 y 3 = z 3 Q = ( 1 0 − 3 2 0 1 − 1 2 0 0 1 ) \begin{cases} y_1=z_1-\frac{3}{2}z_3\\ y_2=z_2-\frac{1}{2}z_3\\ y_3=z_3 \end{cases} \quad Q=\begin{pmatrix} 1&0&-\frac{3}{2}\\ 0&1&-\frac{1}{2}\\ 0&0&1 \end{pmatrix} ⎩ ⎨ ⎧y1=z1−23z3y2=z2−21z3y3=z3Q= 100010−23−211 -
根据线性变换乘法和矩阵乘法的关系 ( x = T y = T ( Q z ) = ( T Q ) z ) (\bold{x=Ty=T(Qz)=(TQ)z}) (x=Ty=T(Qz)=(TQ)z),可求得能将 f f f标准化的线性变换 x = C z \bold{x=Cz} x=Cz的变换矩阵 C \bold{C} C为
C = T Q = ( 1 1 0 1 − 1 0 0 0 1 ) ( 1 0 − 3 2 0 1 − 1 2 0 0 1 ) = ( 1 1 − 2 1 − 1 − 1 0 0 1 ) C=TQ =\begin{pmatrix} 1&1&0\\ 1&-1&0\\ 0&0&1 \end{pmatrix} \begin{pmatrix} 1&0&-\frac{3}{2}\\ 0&1&-\frac{1}{2}\\ 0&0&1 \end{pmatrix} =\begin{pmatrix} 1&1&-{2}\\ 1&-1&-1\\ 0&0&1 \end{pmatrix} C=TQ= 1101−10001 100010−23−211 = 1101−10−2−11 -
由式
(1),标准化后的二次型为 f = z 2 − z 2 2 − 2 z 3 2 f=z^2-z_2^2-2z_3^2 f=z2−z22−2z32
-
-
初等变换法
- 正交变换法和配方法需要考虑的东西较多,操作起来不是很方便,下面介绍一种利用初等变化法来求出能够标准化给定二次型的线性变换矩阵
- 这个方法的基本原理和利用初等变换操作求解方阵的逆矩阵相同,都是利用一个 n n n阶单位阵来记录一系列的初等变换,得到想要的矩阵
原理
-
任意实 n n n阶对称阵 A A A都合同于对角阵 Λ \Lambda Λ,即存在可逆矩阵 P \bold P P,使得 P T A P = Λ \bold{P^{T}AP=\Lambda} PTAP=Λ
-
而可逆矩阵 P \bold{P} P可以表示为若干初等矩阵的乘积; P \bold{P} P= P 1 ⋯ P s \bold{P}_1\cdots\bold{P}_s P1⋯Ps,从而有 ( P 1 ⋯ P s ) T A ( P 1 ⋯ P s ) = Λ \bold{(\bold{P}_1\cdots{P}_s)^{T}A(\bold{P}_1\cdots{P}_s)=\Lambda} (P1⋯Ps)TA(P1⋯Ps)=Λ,即 P s T ⋯ P 1 T A P 1 ⋯ P s = Λ \bold{\bold{P}_s^{T}\cdots{P}_{1}^{T}A\bold{P}_1\cdots{P}_s=\Lambda} PsT⋯P1TAP1⋯Ps=Λ
(1) -
初等矩阵的转置仍然是初等矩阵,并且矩阵 A \bold{A} A左乘 P i T \bold{P}_i^{T} PiT并右乘 P i \bold{P}_i Pi相当于对矩阵 A \bold{A} A作成对的同类型同顺序的行列初等变换(原理参考初等矩阵的性质)
-
因此,我们可以通过将 A \bold{A} A经过成对初等变换转换为一个对角阵 Λ \bold\Lambda Λ
- 这个过程对应于
(1),每一次初等行变换对应于 P T i \bold{P^{T}}_i PTi,绑定的列变换对应于 P i \bold{P}_i Pi - 容易发现 P \bold{P} P= P 1 ⋯ P s \bold{P}_1\cdots\bold{P}_s P1⋯Ps,因此再整个对角化过程中,只需要收集每一次的列变换
- 收集 P 1 ⋯ P s \bold{P}_1\cdots\bold{P}_s P1⋯Ps的方法是用一个 n n n阶单位阵同步对角化过程中的所有列变换
- 原理是: E P 1 ⋯ P s \bold{E}\bold{P}_1\cdots\bold{P}_s EP1⋯Ps= E P \bold{EP} EP= P \bold{P} P
- 我们对行变换不感兴趣,当然行变换也是可以的,求出的是 P T \bold{P}^T PT,需要再次转置才能得到 P \bold{P} P,因此我们直接选择收集列变换更加直接
- 这个过程对应于
-
这部分对初等变换法求解标准化二次型的线性可逆变换矩阵的可行性和正确性给出证明,并且给出了具体的操作方法
总结初等变换法的步骤
-
构造松散分块矩阵 ( A E ) \bold{\binom{A}{E}} (EA)并执行初等变换
-
之所以称为松散,因为我们在将 A A A变换为 Λ \Lambda Λ时,分块E只需要接收列变换 P 1 P 2 ⋯ P s \bold{P_1P_2\cdots{P_s}} P1P2⋯Ps,而不需要做行变换(即忽略行变换)
-
在实际的操作中,可以分为行变换阶段和列变换阶段
- 我们可以先将矩阵 A \bold{A} A用一系列的初等行变换化为上三角矩阵,这部分变换对应于 L = P s T ⋯ P 1 T A \bold{L=\bold{P}_s^{T}\cdots{P}_{1}^{T}}\bold{A} L=PsT⋯P1TA,即依次执行 P 1 T ⋯ P s T \bold{P}_1^{T}\cdots\bold{P}_s^{T} P1T⋯PsT
- L = ( P s T ( ⋯ ( P 1 T A ) ⋯ ) ) \bold{L=(\bold{P}_s^{T}(\cdots({P}_{1}^{T}A)\cdots))} L=(PsT(⋯(P1TA)⋯))
- 然后再执依次行对应的列变换 P 1 ⋯ P s \bold{{P}_{1}\cdots{P}_{s}} P1⋯Ps
- R = ( ( ⋯ ( L P 1 ) ⋯ ) P s ) \bold{R=((\cdots(\bold{L}\bold{P}_1)\cdots){P}_s)} R=((⋯(LP1)⋯)Ps)
- 显然 Λ = R = P s T ⋯ P 1 T A P 1 ⋯ P s \bold{\Lambda=R=\bold{P}_s^{T}\cdots{P}_{1}^{T}A\bold{P}_1\cdots{P}_s} Λ=R=PsT⋯P1TAP1⋯Ps
- 可见这种变换顺序是正确的
- 我们可以先将矩阵 A \bold{A} A用一系列的初等行变换化为上三角矩阵,这部分变换对应于 L = P s T ⋯ P 1 T A \bold{L=\bold{P}_s^{T}\cdots{P}_{1}^{T}}\bold{A} L=PsT⋯P1TA,即依次执行 P 1 T ⋯ P s T \bold{P}_1^{T}\cdots\bold{P}_s^{T} P1T⋯PsT
-
当 A \bold{A} A被一系列成对的初等行列变换转为对角阵 Λ \Lambda Λ,则记录列变换的 E \bold{E} E也就变成了 P = P 1 P 2 ⋯ P s \bold{P=P_1P_2\cdots{P_s}} P=P1P2⋯Ps
-
-
因此 P , Λ \bold{P,\Lambda} P,Λ是同时被求解出来:
- 得到的 P \bold{P} P就是能够满足 P T A P = Λ \bold{P^{{T}}AP=\Lambda} PTAP=Λ(即,使二次型标准化)的可逆矩阵,对应的线性变换为 x = P y \bold{x=Py} x=Py
例
-
用初等变换法将 f ( x 1 , x 2 , x 3 ) f(x_1,x_2,x_3) f(x1,x2,x3)= x 1 2 + 2 x 2 2 + 2 x 3 2 − 2 x 1 x 2 + 4 x 1 x 3 − 6 x 2 x 3 x_1^2+2x_2^2+2x_3^2-2x_1x_2+4x_1x_3-6x_2x_3 x12+2x22+2x32−2x1x2+4x1x3−6x2x3
-
解
-
f f f的系数矩阵为
-
A = ( 1 − 1 2 − 1 2 − 3 2 − 3 2 ) \bold{A}=\begin{pmatrix} 1&-1&2\\ -1&2&-3\\ 2&-3&2 \end{pmatrix} A= 1−12−12−32−32
-
将 A \bold{A} A进初等变换化为对角阵 Λ \bold\Lambda Λ
-
先执行初等列变换 L = P 1 T ⋯ P s T A \bold{L}=\bold{P}_1^{T}\cdots\bold{P}_s^{T}\bold{A} L=P1T⋯PsTA使 A \bold{A} A化为上三角阵
-
A → r 2 + r 1 ; r 3 − 2 r 1 ( 1 − 1 2 0 1 − 1 0 − 1 − 2 ) → r 3 + r 2 ( 1 − 1 2 0 1 − 1 0 0 − 3 ) = L \bold{A}\xrightarrow{r_2+r_1;r_3-2r_1} \begin{pmatrix} 1&-1&2\\ 0&1&-1\\ 0&-1&-2 \end{pmatrix} \xrightarrow{r_3+r_2} \begin{pmatrix} 1&-1&2\\ 0&1&-1\\ 0&0&-3 \end{pmatrix} =\bold{L} Ar2+r1;r3−2r1 100−11−12−1−2 r3+r2 100−1102−1−3 =L
-
再依次地执行对称的列变换 R = L P 1 ⋯ P s \bold{R}=\bold{L}\bold{P}_1\cdots\bold{P}_s R=LP1⋯Ps
(1) -
L → c 2 + c 1 ; c 3 − 2 c 1 ( 1 0 0 0 1 − 1 0 0 − 3 ) → c 3 + c 2 ( 1 0 0 0 1 0 0 0 − 3 ) = R \bold{L}\xrightarrow{c_2+c_1;c_3-2c_1} \begin{pmatrix} 1&0&0\\ 0&1&-1\\ 0&0&-3 \end{pmatrix} \xrightarrow{c_3+c_2} \begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&-3 \end{pmatrix} =\bold{R} Lc2+c1;c3−2c1 1000100−1−3 c3+c2 10001000−3 =R
-
再计算 P = E P 1 ⋯ P s \bold{P}=\bold{E}\bold{P}_1\cdots\bold{P}_s P=EP1⋯Ps
(2) -
E = ( 1 0 0 0 1 0 0 0 1 ) → c 2 + c 1 ; c 3 − 2 c 1 ( 1 1 − 2 0 1 0 0 0 1 ) → c 3 + c 2 ( 1 1 − 1 0 1 1 0 0 1 ) = P \bold{E}=\begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{pmatrix} \xrightarrow{c_2+c_1;c_3-2c_1} \begin{pmatrix} 1&1&-2\\ 0&1&0\\ 0&0&1 \end{pmatrix} \xrightarrow{c_3+c_2} \begin{pmatrix} 1&1&-1\\ 0&1&1\\ 0&0&1 \end{pmatrix} =\bold{P} E= 100010001 c2+c1;c3−2c1 100110−201 c3+c2 100110−111 =P
-
-
从而 Λ = R = ( 1 0 0 0 1 0 0 0 − 3 ) \bold{\Lambda=R}=\begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&-3 \end{pmatrix} Λ=R= 10001000−3 ; P = ( 1 1 − 1 0 1 1 0 0 1 ) \bold{P}=\begin{pmatrix} 1&1&-1\\ 0&1&1\\ 0&0&1 \end{pmatrix} P= 100110−111
-
即线性变换 x = P y \bold{x=Py} x=Py代入 f ( x ) f(\bold{x}) f(x),得标准形 f ( x ) = f ( P y ) f(\bold{x})=f(\bold{Py}) f(x)=f(Py)= g ( y ) g(\bold{y}) g(y)= y T Λ y \bold{y^T\Lambda{y}} yTΛy,其中 x = ( x 1 , x 2 , x 3 ) \bold{x}=(x_1,x_2,x_3) x=(x1,x2,x3), y = ( y 1 , y 2 , y 3 ) \bold{y}=(y_1,y_2,y_3) y=(y1,y2,y3)
-
用求和式表示为 f f f= y 1 2 + y 2 2 − 3 y 3 2 y_1^2+y_2^2-3y_3^2 y12+y22−3y32
-
相关文章:

LA@二次型@标准化相关原理和方法
文章目录 标准化方法正交变换法🎈求矩阵的特征值求各特征值对应的线性无关特征向量组正交化各个向量组 配方法步骤例例 初等变换法原理总结初等变换法的步骤例 标准化方法 正交变换法🎈 二次型可标准化定理的证明过程给出使用二次型标准化的步骤 该方法…...

Git与IDEA: 解决`dev`分支切换问题及其背后原因 为何在IDEA中无法切换到`dev`分支?全面解析!
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

什么是JavaScript中的严格模式(strict mode)?应用场景是什么?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 严格模式(Strict Mode):⭐ 使用场景⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅&…...

红外特征吸收峰特征总结(主要基团的红外特征吸收峰)
特此记录 anlog 2023年9月11日...

ChatGPT AIGC 完成关联分析散点图的应用
关联分析是数据分析中非常重要的一种技术手段,它能够帮助我们在大量数据中发现变量之间的关系和相互影响。在数据分析领域,关联分析被广泛应用于市场营销、销售预测、客户行为分析等领域。 关联分析的主要功能是通过挖掘数据中的关联规则,来发现数据集中事物之间的关联性。…...
开机自启)
CentOS7.6上实现Spring Boot(JAR包)开机自启
前言 Linux自启(或开机自启)指的是在Linux系统启动时自动运行特定的程序或脚本。当计算机启动时,操作系统会按照一定的顺序加载系统服务和配置,其中包括自动启动一些应用程序或服务。这些应用程序或服务会在系统启动后自动运行&a…...

Java开发之框架(spring、springmvc、springboot、mybatis)【面试篇 完结版】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、框架知识分布二、Spring1. spring-单例bean① 问题引入② 单例bean是线程安全的吗③ 问题总结④ 实战面试 2. spring-AOP① 问题引入② AOP记录操作日志③ …...

QT人脸识别知识
机器学习的作用:根据提供的图片模型通过算法生成数据模型,从而在其它图片中查找相关的目 标。 级联分类器:是用来人脸识别。 在判断之前,我们要先进行学习,生成人脸的模型以便后续识别使用。 人脸识别器:…...

熟悉Redis6
NoSQL数据库简介 技术发展 技术的分类 1、解决功能性的问题:Java、Jsp、RDBMS、Tomcat、HTML、Linux、JDBC、SVN 2、解决扩展性的问题:Struts、Spring、SpringMVC、Hibernate、Mybatis 3、解决性能的问题:NoSQL、Java线程、Hadoop、Nginx…...

ip地址会随网络变化而变化吗
随着科技的飞速发展,互联网已深入我们生活的方方面面。在这庞大的网络世界中,IP地址作为网络通信的基础元素,引起了广泛关注。网络变化与IP地址之间存在着密切的关系。那么,IP地址是否会随着网络变化而变化呢?虎观代理…...

QT连接服务器通信,客户端以及服务器端
服务器端 .h文件 #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QTcpServer> //服务器头文件 #include <QTcpSocket> //客户端头文件 #include <QList> //链表头文件,用来存放客户端容器 #include <QDebug> #i…...

Vuex仓库的创建
vuex 的使用 - 创建仓库 文章目录 vuex 的使用 - 创建仓库1.安装 vuex2.新建 store/index.js 专门存放 vuex3.创建仓库 store/index.js4 在 main.js 中导入挂载到 Vue 实例上5.测试打印Vuex 1.安装 vuex 安装vuex与vue-router类似,vuex是一个独立存在的插件&#x…...
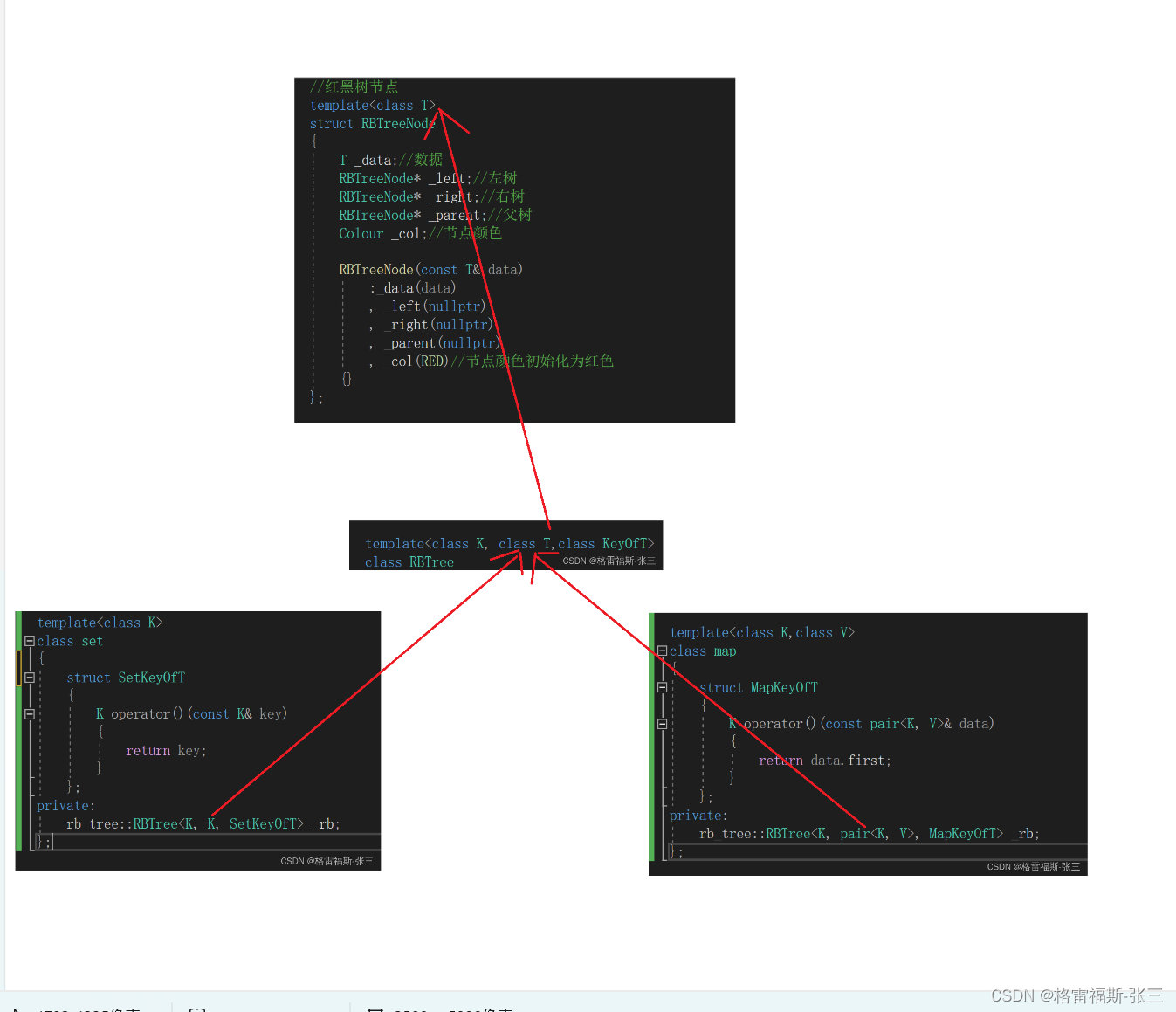
C++中的红黑树
红黑树 搜索二叉树搜索二叉树的模拟实现平衡搜索二叉树(AVL Tree)平衡搜索二叉树的模拟实现红黑树(Red Black Tree)红黑树的模拟实现 红黑树的应用(Map 和 Set)Map和Set的封装 搜索二叉树 搜索二叉树的概念:二叉搜索树又称二叉排序树,它或者是一棵空树&…...

SQL语法知识回顾
一、SQL语言的分类 由于数据库管理系统(数据库软件)功能非常多,不仅仅是存储数据,还要包含:数据的管理、表的管理、库的管理、账户管理、权限管理等等。所以,操作数据库的SQL语言,也基于功能&am…...
)
Java基础二十七(泛型)
泛型 Java 泛型(generics)是 JDK 5 中引入的一个新特性, 泛型提供了编译时类型安全检测机制,该机制允许程序员在编译时检测到非法的类型。 泛型的本质是参数化类型,也就是说所操作的数据类型被指定为一个参数。 Java的泛型是伪…...

Python入门教程36:urllib网页请求模块的用法
urllib是Python中的一个模块,它提供了一些函数和类,用于发送HTTP请求、处理URL编码、解析URL等操作。无需安装即可使用,包含了4个模块: #我的Python教程 #官方微信公众号:wdPythonrequest:它是最基本的htt…...

LeetCode 每日一题 2023/9/4-2023/9/10
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录 9/4 449. 序列化和反序列化二叉搜索树9/5 2605. 从两个数字数组里生成最小数字9/6 1123. 最深叶节点的最近公共祖先9/7 2594. 修车的最少时间9/8 2651. 计算列车到站时间9/…...
C# Onnx Yolov8 Seg 分割
效果 项目 代码 using Microsoft.ML.OnnxRuntime; using Microsoft.ML.OnnxRuntime.Tensors; using OpenCvSharp; using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System…...

Postman接口测试流程
一、工具安装 ● 安装Postman有中文版和英文版,可以选择自己喜欢的版本即可。安装时重新选择一下安装路径(也可以默认路径),一直下一步安装完成即可。(本文档采用英文版本)安装文件网盘路径链接࿱…...

探索GreatADM:如何快速定义监控
引文 在数据库运维过程中,所使用的运维管理平台是否存在这样的问题: 1、默认监控粒度不够,业务需要更细颗粒度的监控数据。2、平台默认的监控命令不适合,需要调整阈值量身定制监控策略。3、不同类型的实例或组件需要有不同的监控重点,但管理平台监控固…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
