栈 之 如何实现一个栈
前言
栈最鲜明的特点就是后进先出,一碟盘子就是类似这样的结构,最晚放上去的,可以最先拿出来。本文将介绍的是如何自己实现一个栈结构。
栈的操作
栈是一种先进后出(Last-In-First-Out, LIFO)的数据结构,常见操作包括:
1、入栈(Push):将元素压入栈顶。
2、出栈(Pop):弹出栈顶元素并返回其值。
3、查看栈顶元素(Peek):返回栈顶元素的值,但不对栈进行修改。
4、判断栈是否为空(isEmpty):检查栈是否为空,如果栈中没有任何元素,则返回 true;否则返回 false。
5、获取栈的大小(size):返回栈中元素的数量。
6、清空栈(clear):清除栈中的所有元素,使其变为空栈。
这些是栈的基本操作。栈的实际使用还可能涉及其他操作,如遍历栈、搜索特定元素、栈的深度等等。根据具体的需求,你可以针对栈的特性来自定义其他更复杂的操作。
栈的实现
栈是较容易实现的抽象数据结构之一。我们可以选择数组或者链表来实现,它们各有特点,前者容量有限且固定,但操作简单,而后者容量理论上不受限,但是操作并不如数组方便,每次入栈要进行内存申请,出栈要释放内存,稍有不慎便造成内存泄露。本文对两种实现都做介绍。
1、用数组实现栈
数组之你值得了解的底层
/*** 用数组实现一个栈*/
public class MyStack {private int maxSize; //栈的大小private int[] stackArray; // 数组,模拟一个栈,用于存放private int top = -1; // 表示栈顶,初始为-1public MyStack(int maxSize) {this.maxSize = maxSize;stackArray = new int[this.maxSize];}public void push(int value) {//判断是否栈满if(isFull()){System.out.println("栈满了..");return;}stackArray[++top] = value;}//弹出栈顶的元素并返回public int pop(int value) {//判断栈是否为空if(isEmpty()) {throw new RuntimeException("栈空,没有数据~~");}value = stackArray[top--];return value;}//查看栈顶的元素public int peek() {//判断栈是否为空if(isEmpty()) {throw new RuntimeException("栈空,没有数据~~");}return stackArray[top];}// 显示栈中的数据-从栈顶开始显示public void list() {// 判断是否栈空if (isEmpty()) {System.out.println("栈空~~");return;}//从栈顶开始展示数据for (int i = top; i >= 0; i--) {System.out.printf("stack[%d]=%d\n", i, stackArray[i]);}}//栈空public boolean isEmpty() {return top == -1;}//栈满public boolean isFull() {return top == (maxSize - 1);}
}2、用队列实现栈
Java两个队列实现一个栈
3、用链表实现栈
/*** @Description* @Author Flag* @Date: 2021/7/20 8:53* @Version: 1.0**/
public class LinkedStackDome {public static void main(String[] args) {//测试一下LinkedStack是否正常//先创建一个ArrayStack对象->表示栈LinkedStack stack = new LinkedStack(4);String key = "";boolean loop = true;//用于控制是否退出Scanner scanner = new Scanner(System.in);while (loop){System.out.println("show:表示显示栈");System.out.println("exit:退出程序");System.out.println("push:表示添加元素到栈(入栈)");System.out.println("pop:表示从栈取出数据(出战)");System.out.println("请输入你的选择:");key = scanner.next();switch (key){case "show":stack.show();break;case "exit":scanner.close();loop = false;break;case "push":System.out.println("请输入一个数字");int i = scanner.nextInt();stack.push(i);break;case "pop":try{int pop = stack.pop();System.out.println("出栈的数据:"+pop);} catch (Exception e){System.out.println(e.getMessage());}break;default:break;}}}}class LinkedStack{//定义栈的大小private int maxSize;//链表模拟栈,private LinkedStackNode first;//top表示栈顶,初始化是-1private int top;/*** 构造方法* @param maxSize 栈的大小*/public LinkedStack(int maxSize) {this.maxSize = maxSize;top = -1;}/*** 判断栈是否满了* @return*/public boolean isFull(){return top+1 == maxSize;}/*** 入栈* @param value 入栈的元素*/public void push(int value){//1、判断栈是否满了if(this.isFull()){System.out.println("栈已经满了,不能再添加元素");return;}//2、新创建一个节点,用于添加到链表上LinkedStackNode node = new LinkedStackNode(value);//3、将top++,表示链表中的元素新增了一个top++;//4、判断头元素是否为null,如果是null,代表是第一个元素,则直接让新元素当第一个元素if(first == null){first = node;return;}//5.如果头元素不是null,则证明,此时链表中已经有元素,则将新元素添加上即可//5.1获取到链表的尾部LinkedStackNode middleNode = first;while (middleNode.getNext() != null){middleNode = middleNode.getNext();}//5.2将链表添加上去middleNode.setNext(node);}/*** 出栈* @return 出栈的元素*/public int pop(){//1.判断栈是否为nullif(this.isEmpty()){throw new RuntimeException("栈中没有元素");}//2.将链表的数量减一top -- ;//3.如果链表中是否只有一个元素if(first.getNext() == null){LinkedStackNode popNode = this.first;this.first = null;return popNode.getNumber();}//4.如果链表中有不只一个元素//4.1.定义一个中间变量,让他指向链表的最后一个元素,即最后要出栈的元素LinkedStackNode lastNode = first;//4.2.定义一个中间变量,用来用来获取到比lastNode前一个元素,‘//因为是单向链表,我们出栈后,要置空指向最后一个元素的指针,所以需要找到最有一个元素的前一个元素进行操作LinkedStackNode beforeLastNode = null;//4.2.遍历链表,直到lastNode是最后一个元素,此时,如果链表中只有一个元素,则while (lastNode.getNext() != null){//将lastNode给到beforeLastNode//然后lastNode向后移动//此时就构造出 beforeLastNode在lastNode前一个位置的情况beforeLastNode = lastNode;lastNode = lastNode.getNext();}//4.3.此时将最后一个元素的前一个元素的next指针变成null,则相当于舍弃掉了最后一个元素beforeLastNode.setNext(null);//4.3.返回lastNode的编号return lastNode.getNumber();}/*** 显示栈的元素*/public void show(){//判断栈是否为nullif(this.isEmpty()){System.out.println("栈中无元素");return;}//定义一个新的链表节点LinkedStackNode newLinedStackHead = null;//正向遍历原始链表,将链表的每一个元素,都放到新的链表的第一个元素//因为前面做了判断,所以first不可以为nullLinkedStackNode oldLinkedStackNode = first;//直到原始链表元素为null时,结束while (oldLinkedStackNode != null){LinkedStackNode middleNode = new LinkedStackNode(oldLinkedStackNode.getNumber());if(newLinedStackHead == null){newLinedStackHead = middleNode;} else {middleNode.setNext(newLinedStackHead);newLinedStackHead = middleNode;}//移动原始链表的位置oldLinkedStackNode = oldLinkedStackNode.getNext();}while (newLinedStackHead != null){System.out.println(newLinedStackHead.getNumber());newLinedStackHead = newLinedStackHead.getNext();}}/*** 判断栈是否为null* @return 结果*/public boolean isEmpty(){return top == -1;}
}/*** 链表栈的节点*/
class LinkedStackNode{private int number;private LinkedStackNode next;public LinkedStackNode(int number) {this.number = number;}public int getNumber() {return number;}public LinkedStackNode getNext() {return next;}public void setNext(LinkedStackNode next) {this.next = next;}
}栈的应用
1、栈的应用——递归
1)、递归的定义
递归是一种重要的程序设计方法。简单地说,若在一个函数、过程或数据结构的定义中又应用了它自身,则这个函数、过程或数据结构称为是递归定义的,简称递归。
它通常把一个大型的复杂问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的代码就可以描述岀解题过程所需要的多次重复计算,大大减少了程序的代码量但在通常情况下,它的效率并不是太高。
2)、斐波那契数列
2、栈的应用——四则运算表达式求值
1)、后缀表达式计算结果
2)、中缀表达式转后缀表达式
笔记
相关文章:

栈 之 如何实现一个栈
前言 栈最鲜明的特点就是后进先出,一碟盘子就是类似这样的结构,最晚放上去的,可以最先拿出来。本文将介绍的是如何自己实现一个栈结构。 栈的操作 栈是一种先进后出(Last-In-First-Out, LIFO)的数据结构,…...
uni-app:自带的消息提示被遮挡的解决办法(自定义消息提示框)
效果: 代码: 1、在最外层或者根组件的模板中添加一个容器元素,用于显示提示消息。例如: <div class"toast-container" v-if"toastMessage"><div class"toast-content">{{ toastMessa…...
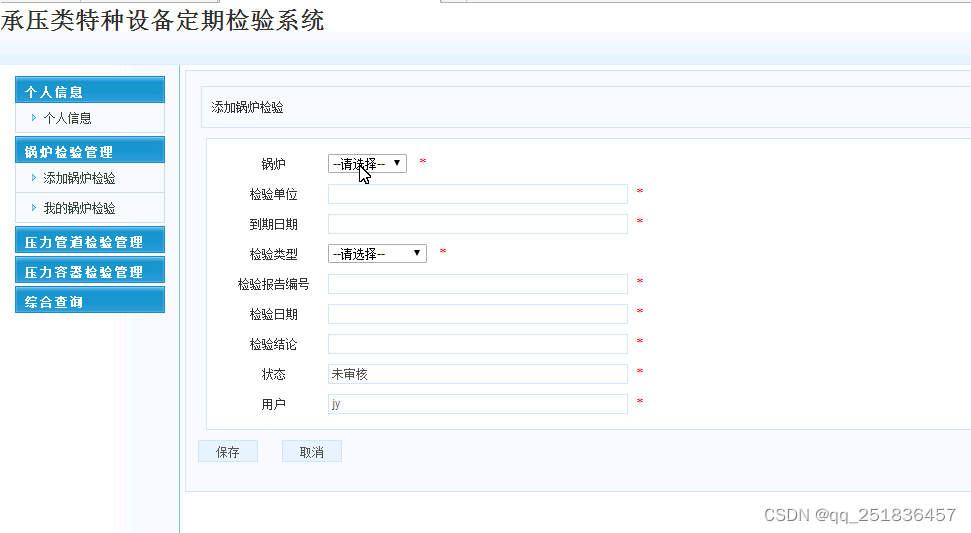
PHP设备检验系统Dreamweaver开发mysql数据库web结构php编程计算机网页代码
一、源码特点 PHP设备检验系统是一套完善的web设计系统,对理解php编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。 下载地址 https://download.csdn.net/download/qq_41221322/88306259 php设备检验系统1 …...
Windows 可以使用以下快捷键打开终端(命令提示符)
Windows 可以使用以下快捷键打开终端(命令提示符) 使用快捷键 Win R 打开 “运行” 对话框,然后输入 “cmd” 并按下 Enter 键。这将打开默认的命令提示符窗口。 使用快捷键 Ctrl Shift Esc 打开任务管理器,然后在 “文件” …...
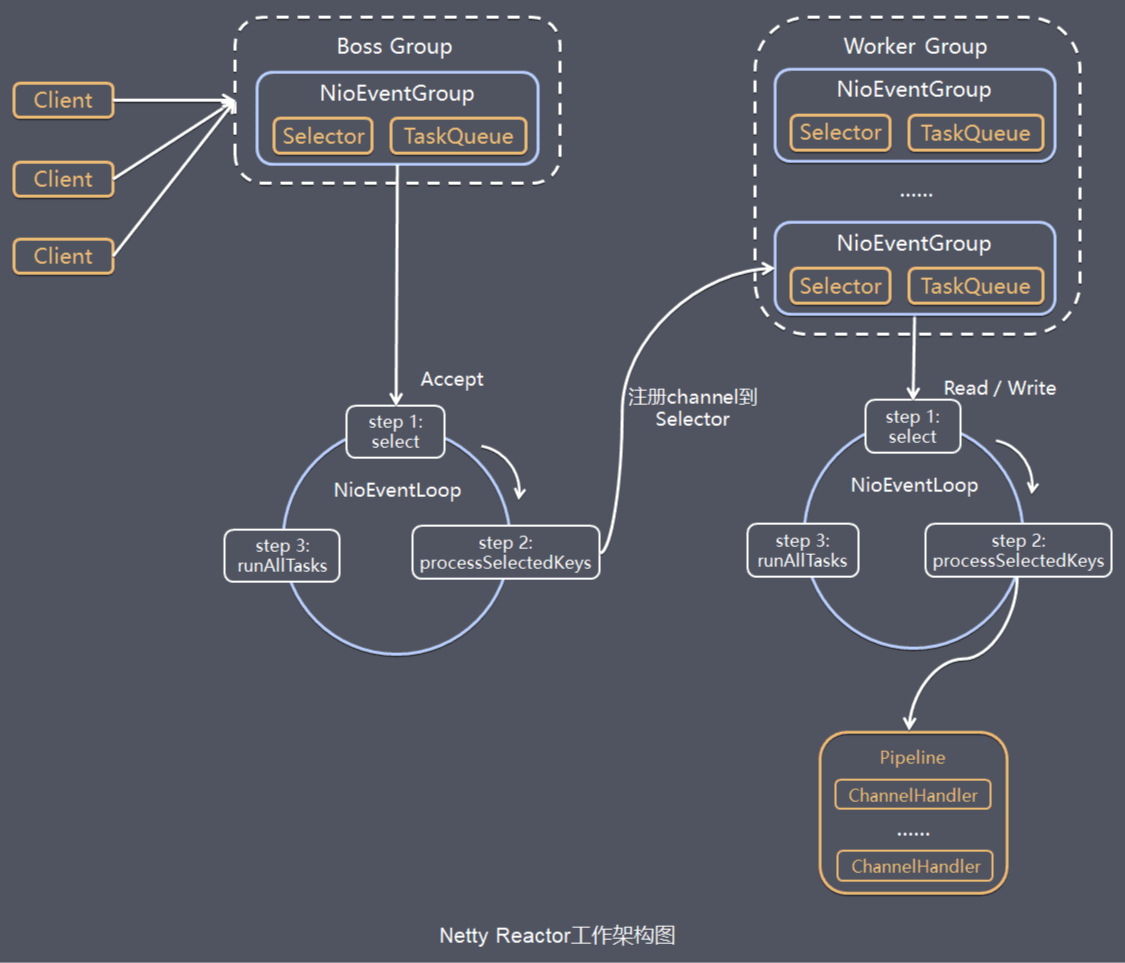
Netty编程面试题
1.Netty 是什么? Netty是 一个异步事件驱动的网络应用程序框架,用于快速开发可维护的高性能协议服务器和客户端。Netty是基于nio的,它封装了jdk的nio,让我们使用起来更加方法灵活。 2.Netty 的特点是什么? 高并发&a…...

math_review
topics mathmatics supreme and optimumNorm and Linear producttopology of R*Continuious Function supreme and optimum Def 1: 非空有界集合必有上确界 common norm (1) x ∈ \in ∈ Rn, ||x||2 x 1 2 x 2 2 . . . x n 2 \sqrt {x_1^2x_2^2...x_n^2} x12x22.…...
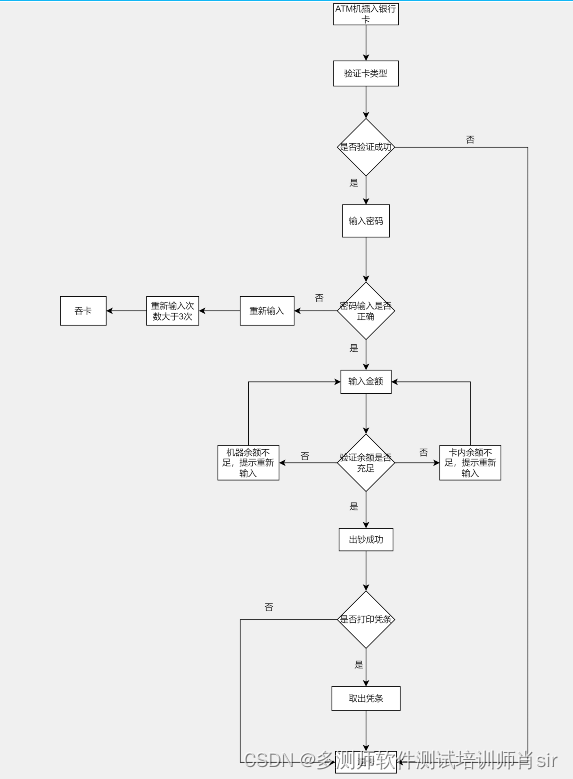
肖sir__设计测试用例方法之场景法04_(黑盒测试)
设计测试用例方法之场景法 1、场景法主要是针对测试场景类型的,顾也称场景流程分析法。 2、流程分析是将软件系统的某个流程看成路径,用路径分析的方法来设计测试用例。根据流程的顺序依次进行组合,使得流程的各个分支能走到。 举例说明&…...

plt函数显示图片 在图片上画边界框 边界框坐标转换
一.读取图片并显示图片 %matplotlib inline import torch from d2l import torch as d2l读取图片 image_path ../data/images/cat_dog_new.jpg # 创建画板 figure d2l.set_figsize() image d2l.plt.imread(image_path) d2l.plt.imshow(image);二.给出一个(x左上角,y左上角,…...

运行期获得文件名和行号
探索动态日志模块的实现 最初的目标是创建一个通用的日志模块, 它具有基本的日志输出功能并支持重定向. 这样, 如果需要更换日志模块, 可以轻松实现. 最初的构想是通过函数重定向, 即使用 dlsym 来重定向所有函数以实现打印功能. 然而, 这种方法引发了一个问题, 即无法正确获…...

数组操作UNIAPP
字符串转数组 let string "12345,56789" string.split(,) // [12345,56789] 数组转字符串 let array ["123","456"] array.join(",") // "123,456" 数组元素删除 let array [123,456] // 删除起始下标为1࿰…...
MySQL——无法打开MySQL8.0软件安装包或者安装过程中失败,如何解决?
在运行MySQL8.0软件安装包之前,用户需要确保系统中已经安装了.Net Framework相关软件,如果缺少此软件,将不能正常地安装MySQL8.0软件。 解决方案:到这个地址 https://www.microsoft.com/en-us/download/details.aspx?id42642…...

DB2存储过程如何编写和执行
db2执行文件参数: -t 表示语句使用默认的语句终结符——分号; -v 表示使用冗长模式,这样 DB2 会显示每一条正在执行命令的信息; -f 表示其后就是脚本文件; -z表示其后的信息记录文件用于记录屏幕的输出&am…...

SpringBoot + FFmpeg实现一个简单的M3U8切片转码系统
简介 在本文中,我们将使用SpringBoot和FFmpeg来实现一个简单的M3U8切片转码系统。M3U8是一种常用的视频流媒体播放列表格式,而FFmpeg则是一个强大的音视频处理工具。 技术栈 SpringBoot:一个基于Spring框架的快速开发平台。FFmpeg…...
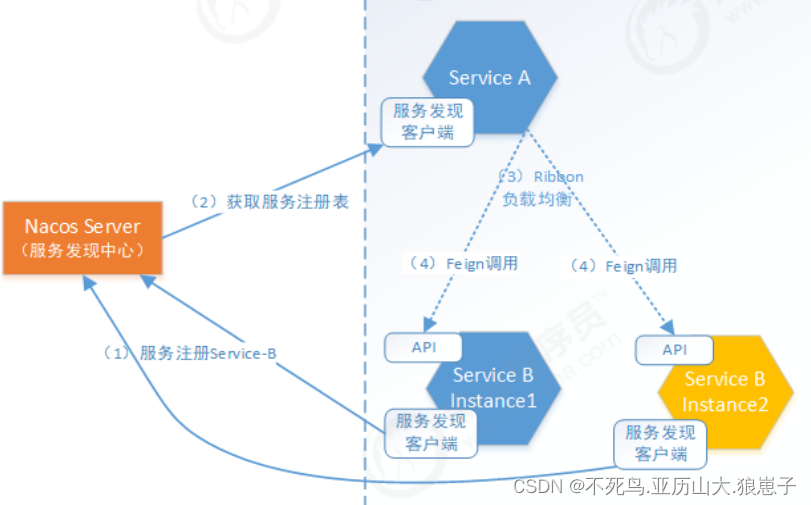
SpringCloud(35):Nacos 服务发现快速入门
本小节,我们将演示如何使用Spring Cloud Alibaba Nacos Discovery为Spring cloud 应用程序与 Nacos 的无缝集成。 通过一些原生的spring cloud注解,我们可以快速来实现Spring cloud微服务的服务发现机制,并使用Nacos Server作为服务发现中心,统一管理所有微服务。 1 Spring…...
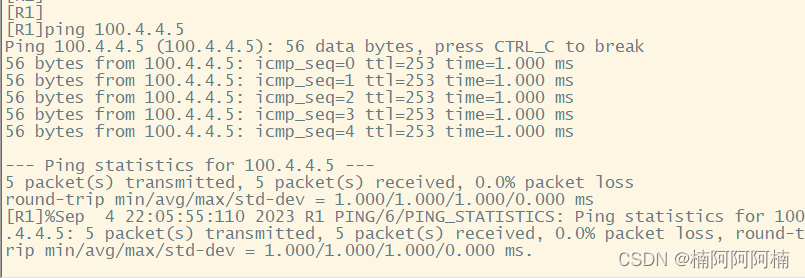
OSPF实验:配置与检测全网互通
文章目录 一、实验背景与目的二、实验拓扑三、实验需求四、实验解法1. 配置 IP 地址2. 按照图示分区域配置 OSPF ,实现全网互通3. 检查是否全网互通 摘要: 本篇文章介绍了一个 OSPF(Open Shortest Path First)实验,旨在…...

常见的五种设计模式
https://www.runoob.com/design-pattern/factory-pattern.html 单例模式 **意图:**保证一个类仅有一个实例,并提供一个访问它的全局访问点。 **主要解决:**一个全局使用的类频繁地创建与销毁。 **何时使用:**当您想控制实例数目…...

pandas读取一个 文件夹下所有excel文件
我这边有个需求,是要求汇总一个文件夹所有的excel文件, 其中有.xls和 .xlsx文件,同时还excel文件中的数据可能还不一致,会有表头数据不一样需要一起汇总。 首先先遍历子文件夹并读取Excel文件: 使用os库来遍历包含子文…...

Python网页请求超时如何解决
在进行网络爬虫项目时,我们经常需要发送大量的请求来获取所需的数据。然而,由于网络环境的不稳定性,请求可能会因为超时而失败。请求超时可能导致数据获取不完整,影响爬虫的效率和准确性。此外,频繁的请求超时可能会被…...

虚幻引擎集成web前端<二>:UE4 像素流 与 web 通信
Vue 和 Unreal Engine (UE) 之间的通信可以通过多种方式实现。以下是一些建议的方法: 使用 Websockets:Websockets 是一种在客户端和服务器之间进行双向通信的技术。在 Vue 端,你可以使用一个 Websockets 库(如 socket.io…...
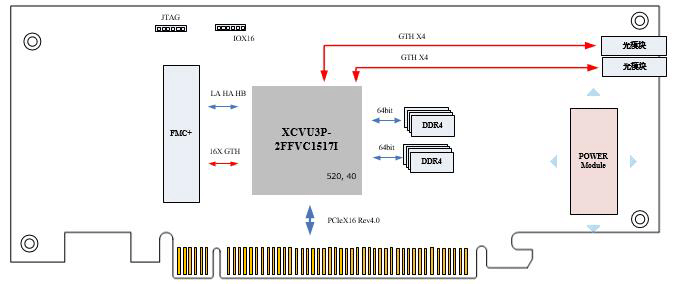
618-基于FMC+的XCVU3P高性能 PCIe 载板 设计原理图
基于FMC的XCVU3P高性能 PCIe 载板 一、板卡概述 板卡主控芯片采用Xilinx UltraScale16 nm VU3P芯片(XCVU3P-2FFVC1517I)。板载 2 组 64bit 的DDR4 SDRAM,支持 IOX16或者 JTAG 口,支持PCIe X 16 ReV3.0以及 FMC 扩展接口。…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
