Fourier傅里叶变换的线性性质和位移性质
Fourier傅里叶变换的线性性质和位移性质
为了阐述方便, 假定在这些性质中, 凡是需要求Fourier变换的函数都满足Fourier积分定理中的条件。在证明这些性质时, 不再重述这些条件。
一、线性性质
设 F 1 ( ω ) = F [ f 1 ( t ) ] {F_1}(\omega ) = {\mathscr F}[{f_1}(t)] F1(ω)=F[f1(t)], F 2 ( ω ) = F [ f 2 ( t ) ] {F_2}(\omega ) = {\mathscr F}[{f_2}(t)] F2(ω)=F[f2(t)], α \alpha α和 β \beta β是常数,则:
F [ α f 1 ( t ) + β f 2 ( t ) ] = α F 1 ( ω ) + β F 2 ( ω ) \mathscr F\left[ {\alpha {f_1}(t) + \beta {f_2}(t)} \right] = \alpha {F_1}(\omega ) + \beta {F_2}(\omega ){\rm{ }} F[αf1(t)+βf2(t)]=αF1(ω)+βF2(ω)
这个性质表明了函数线性组合的Fourier变换等于各函数Fourier变换的线性组合. 它的证明只需根据定义就可推出.
Fourier逆变换亦具有类似的线性性质.
F − 1 [ α F 1 ( ω ) + β F 2 ( ω ) ] = α f 1 ( t ) + β f 2 ( t ) \mathscr {F^{ - 1}} \left[ {\alpha {F_1}(\omega ) + \beta {F_2}(\omega )} \right] = \alpha {f_1}(t) + \beta {f_2}(t) F−1[αF1(ω)+βF2(ω)]=αf1(t)+βf2(t)
二、 位移性质
F [ f ( t ± t 0 ) ] = e ± j ω t 0 F [ f ( t ) ] \mathscr F\left[ {f(t \pm {t_0})} \right] = {{\rm{e}}^{ \pm {\rm{j}}\omega {t_0}}}{\mathscr F}\left[ {f(t)\,} \right] F[f(t±t0)]=e±jωt0F[f(t)]


相关文章:

Fourier傅里叶变换的线性性质和位移性质
Fourier傅里叶变换的线性性质和位移性质 为了阐述方便, 假定在这些性质中, 凡是需要求Fourier变换的函数都满足Fourier积分定理中的条件。在证明这些性质时, 不再重述这些条件。 一、线性性质 设 F 1 ( ω ) F [ f 1 ( t ) ] {F_1}(\omega ) {\mathscr F}[{f_1}(t)] F1(…...

# 磁盘引导方式相关知识之BIOS、msdos、MBR、UEFI、gpt、esp、csm
磁盘引导方式相关知识之BIOS、msdos、MBR、UEFI、gpt、esp、csm 磁盘、分区、引导等知识经常似懂非懂,不能完全说清楚,梳理下: 序号主板芯片引导方式支持的磁盘分区表类型支持的磁盘分区表格式对应引导位置备注1BIOS传统方式(俗…...

Java中同时POST文件和提交JSON数据的方法
一、引言 在Java中,可以使用java.net.URLConnection类来进行HTTP请求,并实现同时POST文件和提交JSON数据的功能。下面将通过一篇文章的形式为您详细讲解这个过程。 二、实现步骤 步骤一:导入所需的类库 首先,你需要导入以下类…...

【React】React获取URL参数,根据URL参数隐藏页面元素
React获取URL参数,根据URL参数隐藏页面元素 AI推荐方法 如果您想使用React获取URL参数并相应地隐藏页面元素,可以按照以下步骤进行操作: 导入React和React DOM: import React from react; import ReactDOM from react-dom;创建…...
第68步 时间序列建模实战:ARIMA建模(Matlab)
基于WIN10的64位系统演示 一、写在前面 这一期,我们使用Matlab进行SARIMA模型的构建。 不同样,这里使用另一个数据: 采用《PLoS One》2015年一篇题目为《Comparison of Two Hybrid Models for Forecasting the Incidence of Hemorrhagic …...
Gin学习记录3——模版与渲染
模版与渲染 一. 返回二. 模版2.1 基础模版2.2 同名模版2.3 模版继承2.4 模版语法 一. 返回 如果只是想返回数据,可以使用以下函数: func (c *Context) JSON(code int, obj any) func (c *Context) JSONP(code int, obj any) func (c *Context) String(…...
Python算法练习 9.11
leetcode 392 判断子序列 给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcd…...

2023年中秋节和国庆节放假几天?用待办软件记录放假安排并提醒
进入公历9月,我们都期待着下个长假的到来。那么2023年中秋节和国庆节放假几天呢?因为今年的中秋节是公历的9月29日,所以今年的中秋节和国庆节是连在一起放假的。放假时间安排是9月29日至10月6日,一共放假8天。而10月7日和8日则是调…...

使用Python实现一个完整的声音采样和模拟,使用采样声音播放输入的文字,实现代码进行详细注释,并进行测试
目录 1.功能概述 2.原理介绍 2.1.声音采样原理 2.2.PCM系统原理 2.3.声音学习与训练...
测试----计算机网络
文章目录 计算机网络的历史OSI/RM 协议TCP/IP协议IP地址 计算机网络的历史 50-60年代 内部通讯功能(连接的是同一台主机,只能主机和终端之间通信,终端和终端之间的通讯只能依靠主机来传输)60-70年代 主机和主机之间能通讯70年代-…...
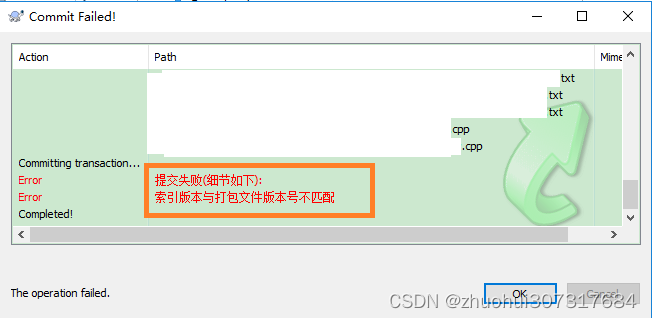
SVN 索引版本与打包版本号不匹配
今天突然遇到了一个问题,SVN上传不了,错误提示如下: 解决方法: 1.其实,这是SVN库不小心搞坏了,只能重新再创建一个SVN仓库了。...
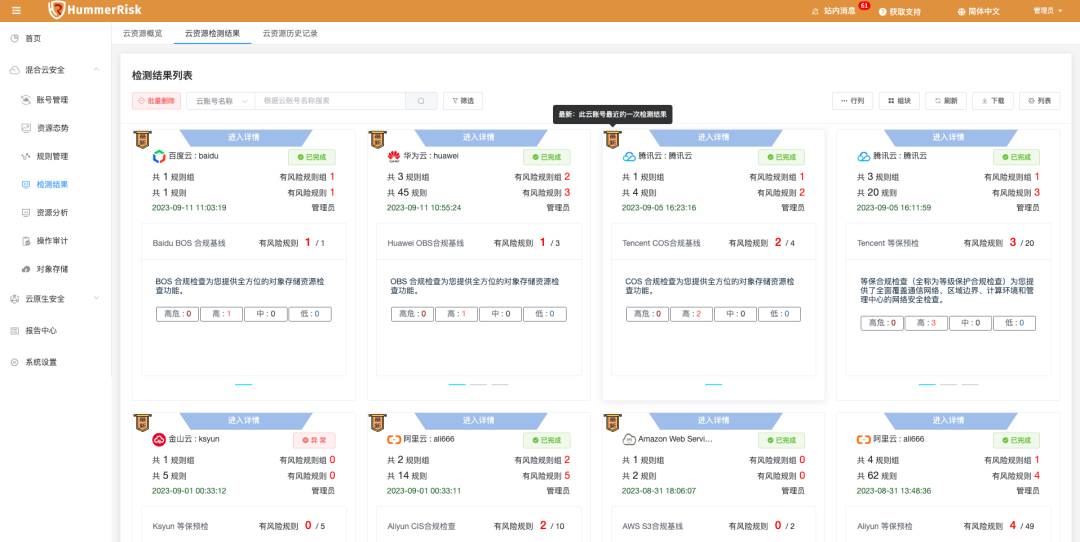
HummerRisk V1.4.1 发布
HummerRisk V1.4.1发布: 大家好,增加检测整合报告下载,定制多云整合报告并下载PDF,增加K8s 检测规则组,Kubernetes、Rancher、KubeSphere 检测规则组以及规则。新增云账号管理页面关联菜单,新增资源同步日…...

php的html实体和字符之间的转换
html_entity_decode() 函数是 htmlentities() 函数的反函数。用于把HTML实体转换为字符。 html_entity_decode() 函数把 HTML 实体转换为字符。 $str "<© W3CSçh°°¦§>"; echo html_entity_decode($str…...

docker-compose deploy 高可用 elasticsearch TLS
文章目录 1.sysctl2. swap3. hosts4. 配置 instances.yaml5. 创建证书6. 部署7. 修改 kibanna 密码8. 清理 1.sysctl [rootgithub es_tls]# cat /etc/sysctl.conf # sysctl settings are defined through files in # /usr/lib/sysctl.d/, /run/sysctl.d/, and /etc/sysctl.d/…...
让GPT成为您的科研加速器丨GPT引领前沿与应用突破之GPT4科研实践技术与AI绘图
GPT对于每个科研人员已经成为不可或缺的辅助工具,不同的研究领域和项目具有不同的需求。如在科研编程、绘图领域:1、编程建议和示例代码:无论你使用的编程语言是Python、R、MATLAB还是其他语言,都可以为你提供相关的代码示例。2、数据可视化…...

工业互联网的破局密钥——低代码开发
纵观历史上三次工业革命的演进过程,以蒸汽机、电力、计算机为相应时代的“新型”基础设施建设,依托“通用技术”的广泛应用,带动了整个行业与市场的发展。 在发展数字经济成为必选题的今天,同样需要一个新型的、基础性的、通用型…...
每天10个小知识点)
JavaScript知识系列(2)每天10个小知识点
目录 系列文章目录JavaScript知识系列(1)每天10个小知识点 知识点**11. 如果 new 一个箭头函数的会怎么样****12. 箭头函数的 this 指向哪⾥?****13. 扩展运算符**的概念、作用、原理、特性、优点、缺点、区别、使用场景**14. Proxy**的概念、…...
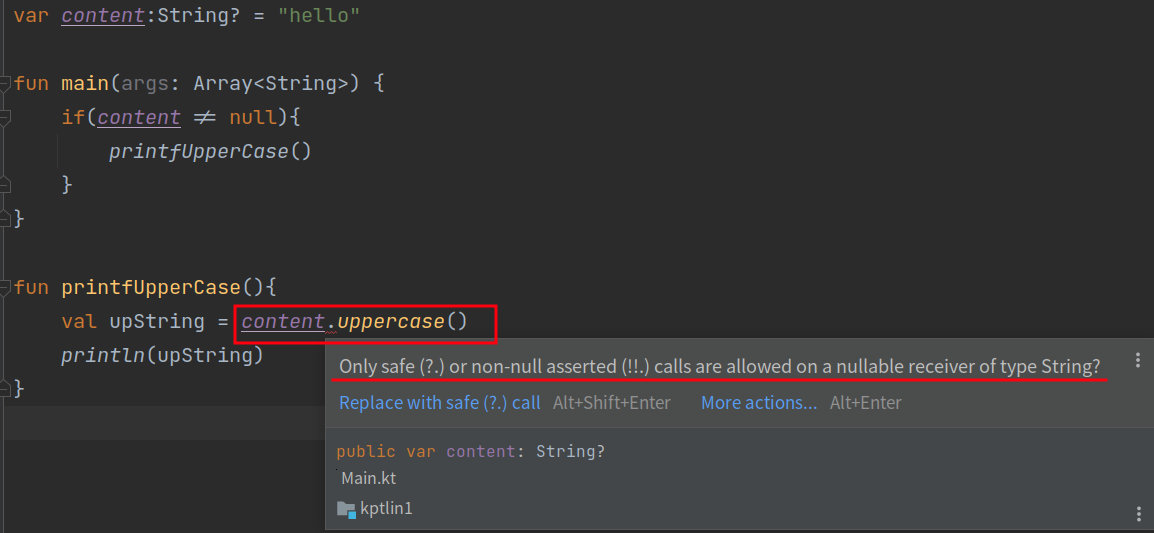
Kotlin面向对象基础使用方法(继承、接口、Lambda、空指针检查机制等)
三、面向对象 1、继承 1.1 open改变类的继承属性 在kotlin设计时默认所有的非抽象类是无法被继承的,如果想要使得一个非抽象类可以被继承,我们需要使用open关键字。 open class Person {var name "";var age 0;fun eat() {println(name …...

Android USB电源管理
The USB peripheral detects the lack of 3 consecutive SOF packets as a suspend request from the USB host. 1 驱动shutdown顺序 系统关机或重启的过程中,会调用设备驱动的shutdown函数来完成设备的关闭操作,有需要的设备可以在驱动中定义该函数。其…...

YOLO目标检测——路标数据集+已标注voc和yolo格式标签下载分享
实际项目应用:自动驾驶、视频监控和安防、物体识别和分类、城市规划和地理信息系统等等数据集说明:YOLO路标目标检测数据集,真实场景的高质量图片数据,数据场景丰富,图片格式为jpg,共900张图片,…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
