LeetCode-77-组合

一:题目描述:
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
二:示例与提示
示例 1:
输入:n = 4, k = 2
输出:
[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4],
]
示例 2:
输入:n = 1, k = 1
输出:[[1]]
提示:
1 <= n <= 201 <= k <= n
三:思路
回溯+剪枝
对于这类组合问题,可以将题目所描述的数组通过组合去构建一个树形结构
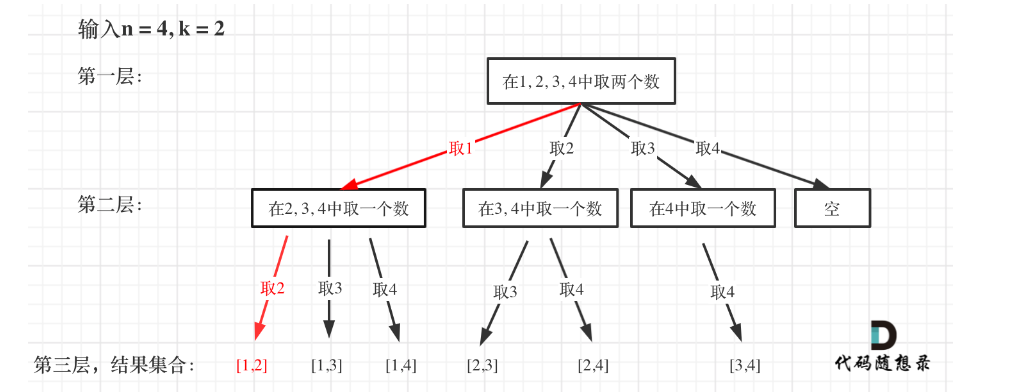
- 横向拓展是数组中的元素个数,从1到n
- 纵向拓展是深度,是对应元素的组合
- 通过不断的递归和回溯,在每一层次中构建组合,搜索到对应的叶子节点
- 图中每次搜索到了叶子节点,我们就找到了一个结果,将结果收集到结果集中即可
四:代码 + 复杂度分析
回溯+剪枝
/*** @param {number} n* @param {number} k* @return {number[][]}*/
var combine = function(n, k) {//回溯//确定回溯函数的参数//存放最终所有结果的数组const res = []//path单层结果const path = []const backtracking = (n, k, index) => {//终止条件if(path.length === k) {console.log(path)//收集结果res.push([...path])return }//单层逻辑for(let i = index; i <= n - (k - path.length) + 1; i++) {//路径收集path.push(i)//递归backtracking(n, k, i + 1)// console.log(path)//回溯path.pop()}}backtracking(n, k, 1)return res
};
-
时间复杂度:O(C(n, k))
- 对于每个数字,我们有两个选择(包括或不包括),并且我们有k个选择(需要选择k个数字)
- 其中C(n, k)表示从n个元素中选择k个元素的组合数,也可以表示为二项式系数
-
空间复杂度:O(k + 2^n)
- 总的空间复杂度是 O(k + 2^n),其中
k反映了递归树的深度,而2^n反映了结果数组res的可能长度
- 总的空间复杂度是 O(k + 2^n),其中
相关文章:

LeetCode-77-组合
一:题目描述: 给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。 你可以按 任何顺序 返回答案。 二:示例与提示 示例 1: 输入:n 4, k 2 输出: [[2,4],[3,4],[2,3],[1,2],[1,3],[1,4…...

Oracle中instr,rtrim,XMLPARSE,XMLAGG,GETCLOBVAL函数的使用
1:INSTR()函数 INSTR 是一个字符串函数,用于查找子字符串在源字符串中的位置。 它的语法如下: INSTR(source_string, search_string)source_string 是源字符串,即要在其中进行搜索的字符串。search_string 是要查找的子字符串。…...
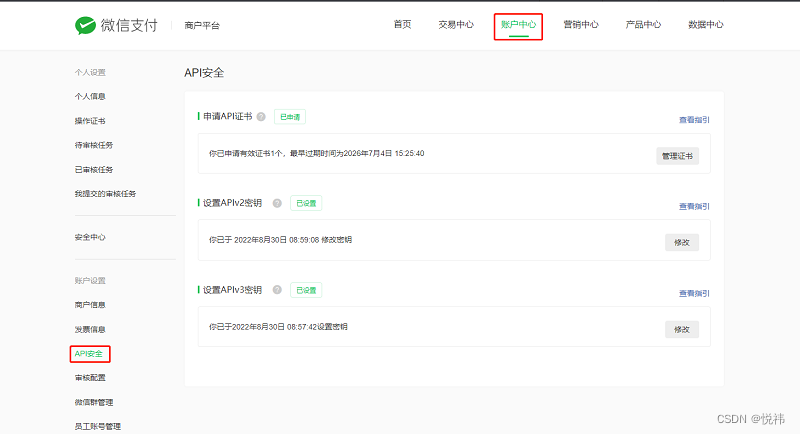
java接入apiv3微信小程序支付(以java的eladmin框架为例)
一、需要准备的资料 1.小程序AppID 如:wx2e56f5****** 2.商户号 如:1641****** 3.商户API私钥路径:什么是商户API证书?如何获取商户API证书? 获取文件如下图: 如: 本地路径:E:\Env\e…...

第19节-PhotoShop基础课程-历史记录画笔工具
文章目录 前言1.历史记录画笔工具1.从当前状态创建文档2.创建新快照 2.历史记录艺术画笔工具 前言 任何记录都会被记录下来,并且可以拍快照,从历史中恢复,特别适合艺术创作的孩子 1.历史记录画笔工具 不只是画笔,所有操作记录都…...
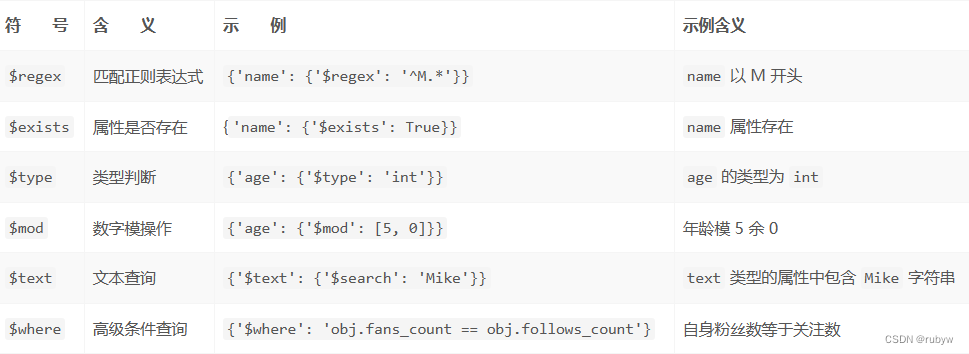
MongoDB常用的比较符号和一些功能符号
比较符号 results collection.find({age: {$gt: 20}})功能符号 results collection.find({name: {$regex: ^M.*}})...

网络安全(黑客)技术自学
前言 一、什么是网络安全 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 无论网络、Web、移动、桌面、云等哪个领域,都有攻与防…...

C++ 引用
C 引用 引用变量是一个别名,也就是说,它是某个已存在变量的另一个名字。一旦把引用初始化为某个变量,就可以使用该引用名称或变量名称来指向变量。 C 引用 vs 指针 引用很容易与指针混淆,它们之间有三个主要的不同:…...

9.1.tensorRT高级(4)封装系列-自动驾驶案例项目self-driving-道路分割分析
目录 前言1. 道路分割总结 前言 杜老师推出的 tensorRT从零起步高性能部署 课程,之前有看过一遍,但是没有做笔记,很多东西也忘了。这次重新撸一遍,顺便记记笔记。 本次课程学习 tensorRT 高级-自动驾驶案例项目self-driving-道路分…...

稳定的 Glance 来了,安卓小部件有救了!
稳定的 Glance 来了,安卓小部件有救了! 稳定版本的 Glance 终于发布了,来一起看看吧,看看这一路的旅程,看看好用么,再看看如何使用! 前世今生 故事发生在两年的一天吧,其实夸张了…...
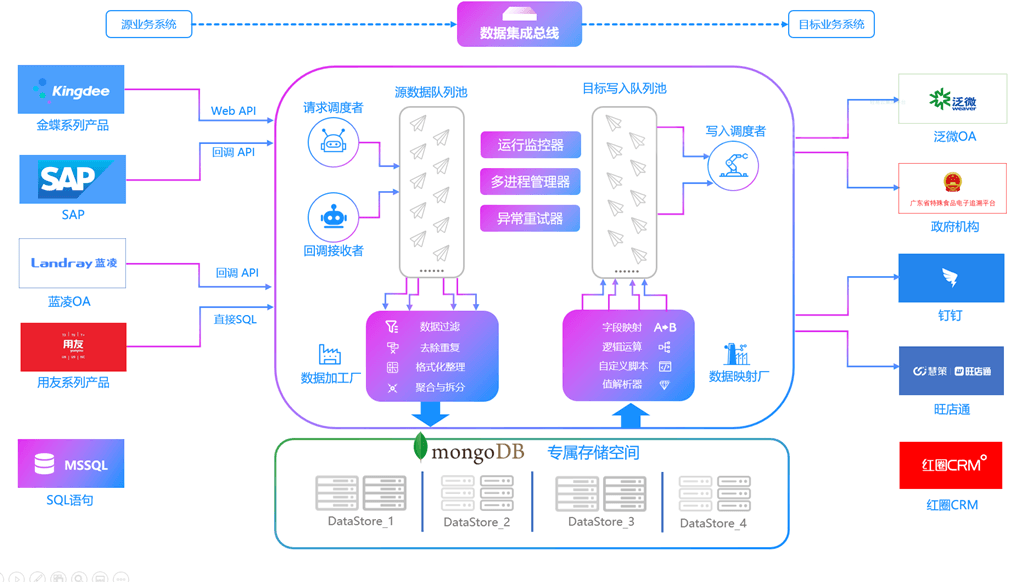
用友U8与MES系统API接口对接案例分析
企业数字化转型:轻易云数据集成平台助力 U8 ERPMES 系统集成 为什么选择数字化转型? 领导层对企业资源规划(ERP)的深刻理解促使了数字化转型的启动。采用精确的“N5”滚动计划,为供应商提供充分的预期信息,…...
web UI自动化介绍
文章目录 一、web UI自动化介绍1.1 执行UI自动化测试前提1.2 Selenium介绍以及知识点梳理 二、Selenium 学习2.1 基础2.1.1 环境安装与基础使用2.1.2 web浏览器控制2.1.3 常见控件的八大定位方式2.1.3.1 八大定位方式介绍2.1.3.2 NAME、ID定位2.1.3.3 css_selector定位2.1.3.4 …...

小米13Pro/13Ultra刷面具ROOT后激活LSPosed框架微X模块详细教程
喜欢买小米手机,很多是因为小米手机的开放,支持root权限,而ROOT对普通用户来说更多的是刷入DIY模块功能,今天ROM乐园小编就教大家如何使用面具ROOT,实现大家日常情况下非常依赖的微X模块功能,体验微X模块的…...

文盘Rust -- 给程序加个日志 | 京东云技术团队
日志是应用程序的重要组成部分。无论是服务端程序还是客户端程序都需要日志做为错误输出或者业务记录。在这篇文章中,我们结合log4rs聊聊rust 程序中如何使用日志。 log4rs类似java生态中的log4j,使用方式也很相似 log4rs中的基本概念 log4rs 的功能组件也由 appe…...
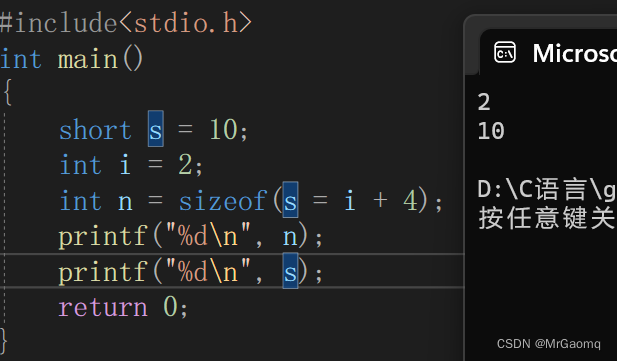
C语言深入理解指针(非常详细)(五)
目录 回调函数qsort使用举例qsort函数的模拟实现sizeof和strlen的对比sizeofstrlensizeof和strlen的对比一道关于sizeof的题 回调函数 回调函数就是一个通过函数指针调用的函数 如果你把函数的指针(地址)作为参数传递给另一个函数,当这个指…...
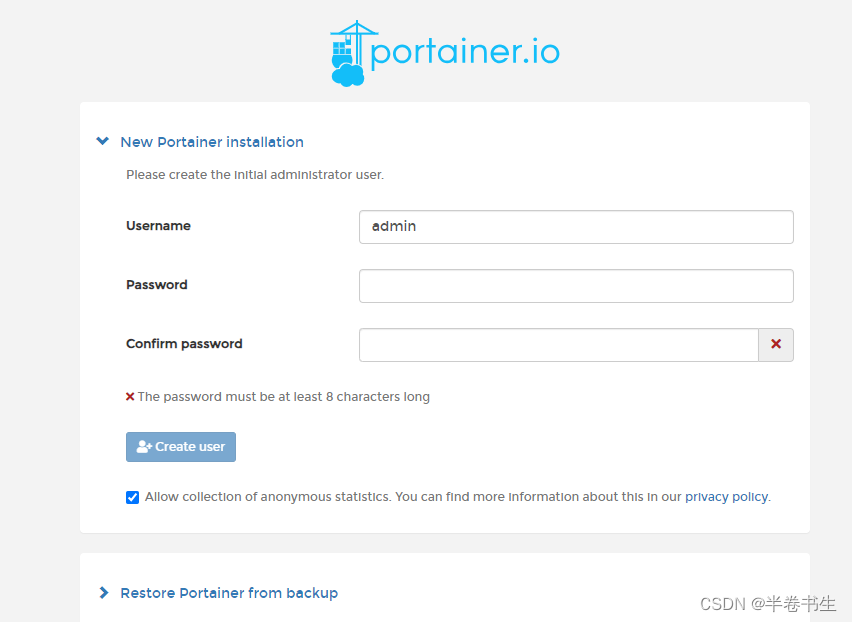
[docker]笔记-portainer的安装
1、portainer是一款可视化的容器管理软件,利用portainer可以轻松方便的管理和创建容器。portainer本身是一个容器,完全免费并且具有汉化版。本文介绍portainer的安装和使用。 2、安装好容器并配置好容器环境,可参照https://blog.csdn.net/bl…...
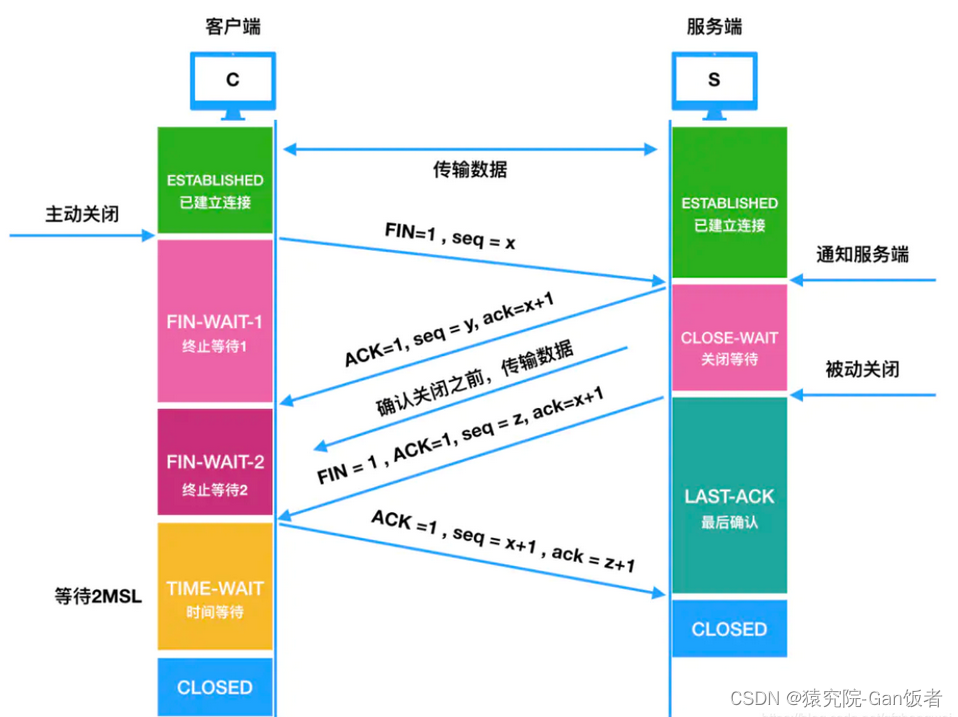
详解TCP/IP的三次握手和四次挥手
文章目录 前言一、TCP/IP协议的三次握手1.1 三次握手流程 二、TCP/IP的四次挥手2.1 四次挥手流程 三、主要字段3.1、标志位(Flags)3.2、序号(sequence number)3.3、确认号(acknowledgement number) 四、状态…...

YOLOv5算法改进(16)— 增加小目标检测层
前言:Hello大家好,我是小哥谈。小目标检测层是指在目标检测任务中用于检测小尺寸目标的特定网络层。由于小目标具有较小的尺寸和低分辨率,它们往往更加难以检测和定位。YOLOv5算法的检测速度与精度较为平衡,但是对于小目标的检测效…...
)
蓝桥杯官网练习题(图像模糊)
题目描述 小蓝有一张黑白图像,由 nm 个像素组成,其中从上到下共 n 行,每行从左到右 �m 列。每个像素由一个 0 到 255 之间的灰度值表示。 现在,小蓝准备对图像进行模糊操作,操作的方法为: 对…...

使用鳄鱼指标和ADX开立空头的条件,3秒讲清楚
使用鳄鱼指标和ADX开立空头的条件其实很简单,anzo capital昂首资本3秒钟讲清楚。 首先,市场行情需呈水平状态。再者,均线体系开始向上发散,给出明确的信号。最后,ADX确认该信号,要求指数上涨20%以上&#…...

RabbitMQ死信队列与延迟队列
目录 死信队列 死信队列的定义 死信队列的应用场景 死信队列的作用 死信队列架构图 死信队列代码实现 延迟队列 延迟队列的定义 延迟队列的应用场景 延迟队列的作用 延迟队列架构图 延迟队列的代码实现 死信队列 死信队列的定义 死信队列(Dead Letter …...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...
