Python中的 if __name__ ==‘main‘
你编写的程序迟早需要创建目录以便在其中存储数据。 os 和 pathlib 包含了创建目录的函数。我们将会考虑如下方法:
| 方法 | 描述 | | -------------------- | -------------------------- | | os.mkdir() | 创建单个子目录 | | os.makedirs() | 创建多个目录,包括中间目录 | | Pathlib.Path.mkdir() | 创建单个或多个目录 |
创建单个目录
import os
os.mkdir("example_directory")
如果该目录已经存在,os.mkdir() 将抛出 FileExistsError 异常。或者,你也可以使用 pathlib 来创建目录:
from pathlib import Pathp = Path('example_directory')
p.mkdir()
如果路径已经存在,mkdir() 会抛出 FileExistsError 异常:
FileExistsError: [Errno 17] File exists: 'example_directory'
为了避免像这样的错误抛出, 当发生错误时捕获错误并让你的用户知道:
from pathlib import Pathp = Path('example_directory')
try:p.mkdir()
except FileExistsError as e:print(e)
或者,你可以给 .mkdir() 传入 exist_ok=True 参数来忽略 FileExistsError 异常:
from pathlib import Pathp = Path('example_directory')
p.mkdir(exist_ok=True)如果目录已存在,则不会引起错误。
创建多个目录
os.makedirs() 和 os.mkdir() 类似。两者之间的区别在于,os.makedirs() 不仅可以创建单独的目录,还可以递归的创建目录树。换句话说,它可以创建任何必要的中间文件夹,来确保存在完整的路径。
os.makedirs() 和在bash中运行 mkdir -p 类似。例如,要创建一组目录像 2018/10/05,你可以像下面那样操作:
import osos.makedirs('2018/10/05', mode=0o770)
上述代码创建了 2018/10/05 的目录结构并为所有者和组用户提供读、写和执行权限。默认的模式为 0o777 ,增加了其他用户组的权限。有关文件权限以及模式的应用方式的更多详细信息,请参考 文档
相关文章:

Python中的 if __name__ ==‘main‘
你编写的程序迟早需要创建目录以便在其中存储数据。 os 和 pathlib 包含了创建目录的函数。我们将会考虑如下方法: | 方法 | 描述 | | -------------------- | -------------------------- | | os.mkdir() | 创建单个子目录 | | os.makedirs() | 创建多个目录&…...

github 创建自己的分支 并下载代码
github创建自己的分支 并下载代码 目录概述需求: 设计思路实现思路分析1.进入到master分支,git checkout master;2.master-slave的个人远程仓库3.爬虫调度器4.建立本地分支与个人远程分支之间的联系5.master 拓展实现 参考资料和推荐阅读 Survive by day…...

算法:贪心---跳一跳
1、题目: 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 2…...

机器学习入门教学——梯度下降、梯度上升
1、简介 梯度表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(梯度的方向)变化最快,变化率(梯度的模)最大,可理解为导数。梯度上升和梯度下降是优化算法中常用的…...
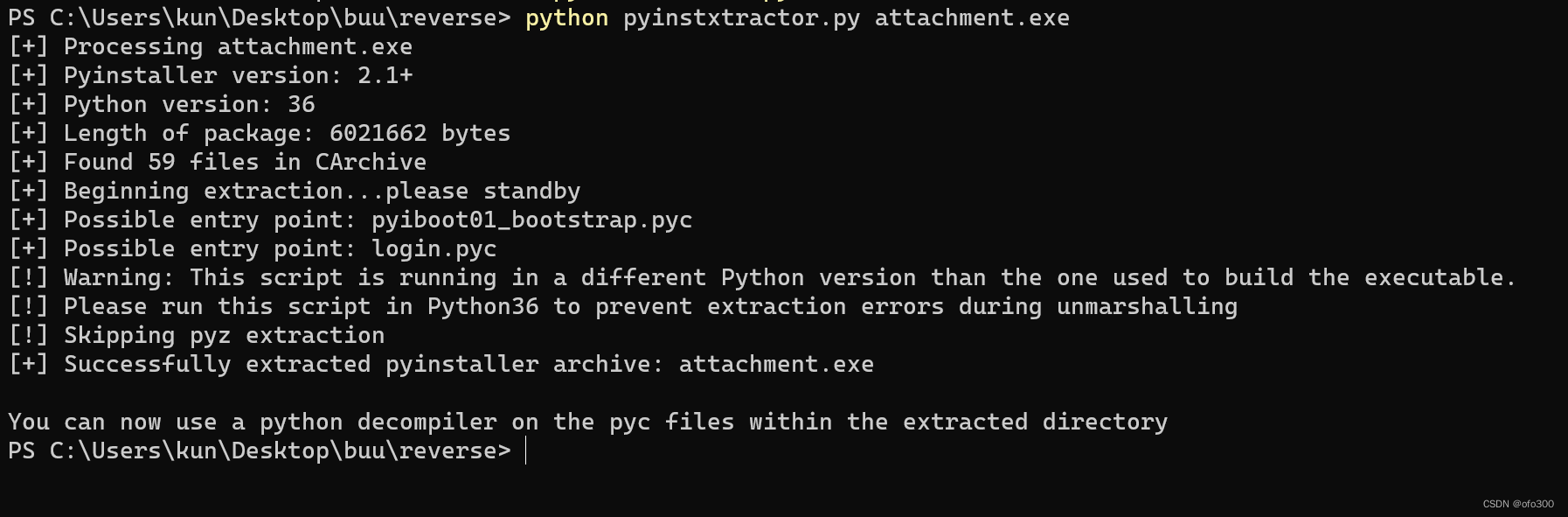
BUUCTF Reverse/[羊城杯 2020]login(python程序)
查看信息,python文件 动调了一下,该程序创建了一个线程来读入数据,而这个线程的代码应该是放在内存中直接执行的,本地看不到代码,很蛋疼 查了下可以用PyInstaller Extractor工具来解包,可以参考这个Python解包及反编译…...

indexDB localForage
一、前言 前端本地化存储算是一个老生常谈的话题了,我们对于 cookies、Web Storage(sessionStorage、localStorage)的使用已经非常熟悉,在面试与实际操作之中也会经常遇到相关的问题,但这些本地化存储的方式还存在一些…...

Spring Boot开发时Java对象和Json对象互转
🙈作者简介:练习时长两年半的Java up主 🙉个人主页:程序员老茶 🙊 ps:点赞👍是免费的,却可以让写博客的作者开兴好久好久😎 📚系列专栏:Java全栈,…...

C++ 多态
引例: #include<iostream> using namespace std; class Animal { public:void speak(){cout<<"动物在说话"<<endl;} }; class Cat:public Animal { public:void speak(){cout<<"小猫在说话"<<endl;} }; void Do…...

LeetCode 之 二分查找
网址: LeetCode 704.二分查找 算法模拟: Algorithm Visualizer 在线工具: C 在线工具 如果习惯性使用Visual Studio Code进行编译运行,需要C11特性的支持,可参考博客: VisualStudio Code 支持C11插件配…...
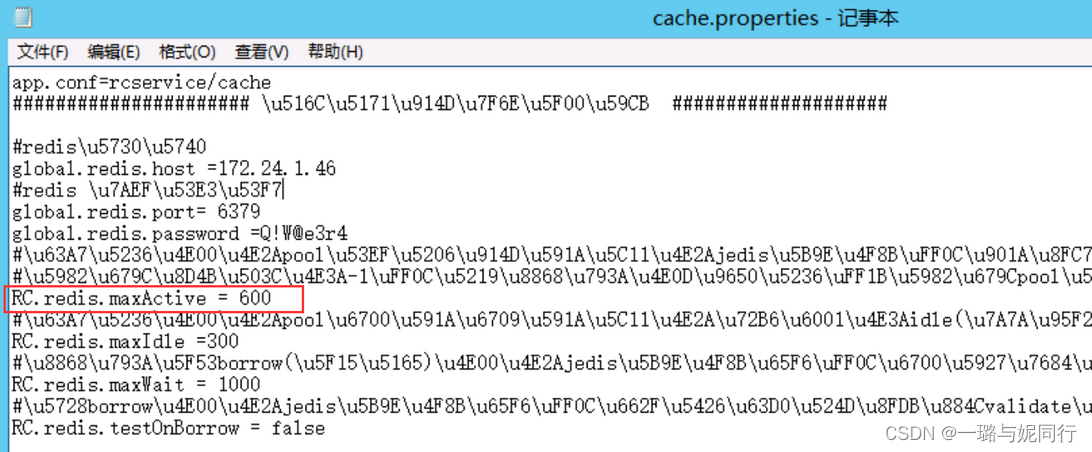
【性能测试】中间件优化
1、Tomcat 优化连接数、线程池 打开tomcat安装目录\conf\server.xml文件,在server.xml中 有以下配置: tomcat HTTP/1.1 <Connector port"8080" protocol"HTTP/1.1" maxThreads"1000" acceptCount"1500" c…...

【算法】查找类——二分查找算法
二分查找算法算法总结 算法描述 该算法属于查找算法。当需要从有序数组中查找某一元素时,可以使用该算法进行查找。(本文章假设数组是升序排列的数组) 算法思想 每次进行对半查找,获取中间元素值,然后与目标值进行…...

Ansible FIle模块,使用Ansible File模块进行文件管理
当使用 Ansible 进行自动化配置和管理时,file 模块是一个强大的工具,用于在目标主机上创建、修改和删除文件和目录。它提供了一种简单而灵活的方式来处理文件系统操作。在本文中,我们将详细介绍如何使用 Ansible 的 file 模块。 1. 创建文件 …...

索尼mp4变成rsv修复案例(ILME-FX3)
索尼mp4的修复案例讲过很多,这次是索尼的ILME-FX3也算是一个畅销的机型,一般索尼没有封装的文件是RSV文件,但是极少遇到有多个RSV文件的,下边我们来讲下这个特殊案例。 故障文件:4个RSV文件,大小在1.78G~28G多 故障现…...

抓拍摄像机开关量控制4K高清手机远程看图建筑生长定时缩时相机
作为物联网数据采集解决方案专业提供商,数采物联网小编daq-iot 在这里做以下内容介绍,并诚挚的欢迎大家讨论和交流。 项目案例参考视频: https://www.bilibili.com/video/BV1Kp4y1T7wQ/?spm_id_from333.999.0.0 4K高清太阳能供电定时拍照相机,通过光…...

c++使用http请求-drogon框架
创建drogon框架 drogon_ctl create project test_ctrl添加一个控制器 进入controllers目录下 drogon_ctl create controller -h check_ctrl编写主函数 #include <drogon/drogon.h> int main() {//Set HTTP listener address and port//drogon::app().addListener("…...

幼儿棒球运动宣传介绍·野球6号位
幼儿棒球运动宣传介绍 1. 棒球对幼儿成长的重要性 棒球运动对幼儿协调能力和团队协作的培养 棒球运动对幼儿协调能力和团队协作的培养非常重要。通过棒球运动,孩子们可以学习如何与队友合作,如何在压力下保持冷静,以及如何快速做出决策。这…...

grpc多语言通信之GO和DART
都是一个吗生的,找下例子 上一篇文章说到go实现的grpc方法已经实现了一个grpc的server端, 注意: 这两个项目的.proto文件应当是完全一致的,只是方法用各自的语言实现罢了 报错了: Caught error: gRPC Error (code: 12, codeName: UNIMPLEMENTED, message: grpc: Decompresso…...

基于FPGA的RGB图像转Ycbcr实现,包括tb测试文件以及MATLAB辅助验证
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 将FPGA的数据导入到matlab进行显示 2.算法运行软件版本 Vivado2019.2 matlab2022a 3.部分核心程序 timescale 1ns / 1ps // // Company: // E…...

centos 编译安装的php多版本 切换
centos 编译安装的php多版本 切换 wheris php php: /usr/bin/php /usr/lib64/php /etc/php.ini /etc/php.d /usr/local/php /usr/local/php7.4 /usr/share/php /usr/share/man/man1/php.1.gz/usr/bin/php: php可执行脚本,任何版本的php 通过软连接到这可以实现全局…...
Unity 性能优化之Shader分析处理函数ShaderUtil.HasProceduralInstancing: 深入解析与实用案例
Unity 性能优化之Shader分析处理函数ShaderUtil.HasProceduralInstancing: 深入解析与实用案例 点击封面跳转到Unity国际版下载页面 简介 在Unity中,性能优化是游戏开发过程中非常重要的一环。其中,Shader的优化对于游戏的性能提升起着至关重要的作用。…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
