lintcode 567 · 最大得分 【动态规划 中等 】
题目
https://www.lintcode.com/problem/567
给定一个矩阵matrix,
matrix[i][j]表示你到达第i行第j列可以得到的分数,现在你要用第0行任意一点出发,从每行里找到一个点进行跳跃,每次从(i,j)到(i+1,k)跳跃需要消耗∣j−k∣的分数,请问到最后一行以后,你最多可以得到多少分。1≤len(matrix),len(matrix[0])≤1000≤matrix[i][j]≤10 ^5样例
样例 1输入:
[[1, 2],[3, 4]]
输出: 6
说明 2 + 4 = 6.
思路
动态规划,下一行依赖上一行
答案
public class Solution {/*** @param matrix: the matrix* @return: the maximum score you can get*/public int maximumScore(int[][] matrix) {//简单的动态规划,认真读题目,看下面的代码//很容易看懂依赖关系int n = matrix.length,m=matrix[0].length;int[][] dp = new int[n][m];for (int j = 0; j < m ; j++) {dp[0][j] = matrix[0][j];}for (int i = 1; i <n ; i++) {for (int j = 0; j <m ; j++) {for (int k = 0; k <m ; k++) {dp[i][j] = Math.max(dp[i][j],dp[i-1][k]-Math.abs(j-k)+matrix[i][j]);}}}int max =Integer.MIN_VALUE;for (int i = 0; i < m; i++) {max=Math.max(max,dp[n-1][i]);}return max;}
}
相关文章:

lintcode 567 · 最大得分 【动态规划 中等 】
题目 https://www.lintcode.com/problem/567 给定一个矩阵matrix, matrix[i][j]表示你到达第i行第j列可以得到的分数,现在你要用第0行任意一点出发,从每行里找到一个点进行跳跃,每次从(i,j)到(i1,k)跳跃需要消耗∣j−k∣的分数&…...

qml嵌入到QWidget的两种方式介绍
本文介绍qml页面嵌入到QWidget的两种方式,以及这两种方式的区别。 方式1 在 Qt 中,可以使用 QQuickWidget 将 QML 内容嵌入到基于 QWidget 的应用程序中。这是在旧的 QWidget-based 应用程序中逐渐引入 QML UI 的一种常见方式。 以下是如何使用 QQuickWidget 将 QML 内容嵌…...

Mysql数据库之常用SQL语句及事务学习总结
数据库介绍 几个常见的缩写: DB:数据库。全称:DataBase。DBMS:数据库管理系统。全称:DataBase Management System。DBS:数据库系统。全称:DataBase System。DBA:数据库管理员。全称…...
RuoYi若依管理系统最新版 基于SpringBoot的权限管理系统
RuoYi是一个后台管理系统,基于经典技术组合(Spring Boot、Apache Shiro、MyBatis、Thymeleaf)主要目的让开发者注重专注业务,降低技术难度,从而节省人力成本,缩短项目周期,提高软件安全质量。 本…...

html实现邮件模版布局-flex布局table布局-demo
邮件模版布局 flex - 布局简单方便 兼容性差 table - 优点 就是兼容性好,其他没有优点 注:使用图片需要png最好,使用svg图google邮箱会出现不能使用的情况 效果图 flex布局 <!DOCTYPE html> <html lang"en" xmlns:th&qu…...

CENTOS7安装redis在/home/pms/software路径下,并且将redis加入到systemctl中
要将/home/software/redis-stack-server-7.2.0-v0/service/redis.service添加到systemctl系统管理,你可以执行以下步骤: 创建软连接: sudo ln -s /home/software/redis-stack-server-7.2.0-v0/service/redis.service /etc/systemd/system/r…...

数据库笔记
数据库原理及应用 半期考:运筹学,概率论,数据库 文章目录 数据库原理及应用1.课程的考核2.数据库的运用3.数据库学什么? 第一章 绪论1.1数据库系统概述1.1.1基本概念1.1.2数据管理技术的生产和发展人工管理文件系统数据库系统 1.…...

AI是风口还是泡沫?
KlipC报道:狂热的人工智能追捧潮有所冷静,投资者在“上头”的追涨之后,开始回归到对基本面的关注。 KlipC的合伙人Andi D表示:“近日,有关英伟达二季度“破纪录”财报涉嫌造假的话题正在社交媒体和投资者论坛中甚嚣尘上…...

echarts环图配置
echarts环图配置 1、安装echarts npm install echarts4.9.02、页面引入echarts import echarts from echarts;3、应用 template片段 <div class"chart-wrap"><div id "treeChart" style "width: 180px; height:180px;" ><…...

Redis优化 RDB AOF持久化
---------------------- Redis 高可用 ---------------------------------------- 在web服务器中,高可用是指服务器可以正常访问的时间,衡量的标准是在多长时间内可以提供正常服务(99.9%、99.99%、99.999%等等)。 但是在Redis语境…...
三维模型3DTILE格式轻量化压缩主要技术方法浅析
三维模型3DTILE格式轻量化压缩主要技术方法浅析 三维模型3DTILE格式轻量化压缩主要技术方法浅析 随着三维地理空间数据的应用日益广泛,为了更快速地传输和存储这些大规模数据,3DTile格式的轻量化压缩显得尤为重要。本文将浅析关于三维模型3DTile格式轻量…...
c++day2---9.7
1> 思维导图 2> 封装一个结构体,结构体中包含一个私有数组,用来存放学生的成绩,包含一个私有变量,用来记录学生个数, 提供一个公有成员函数,void setNum(int num)用于设置学生个数 提供一个公有成员…...
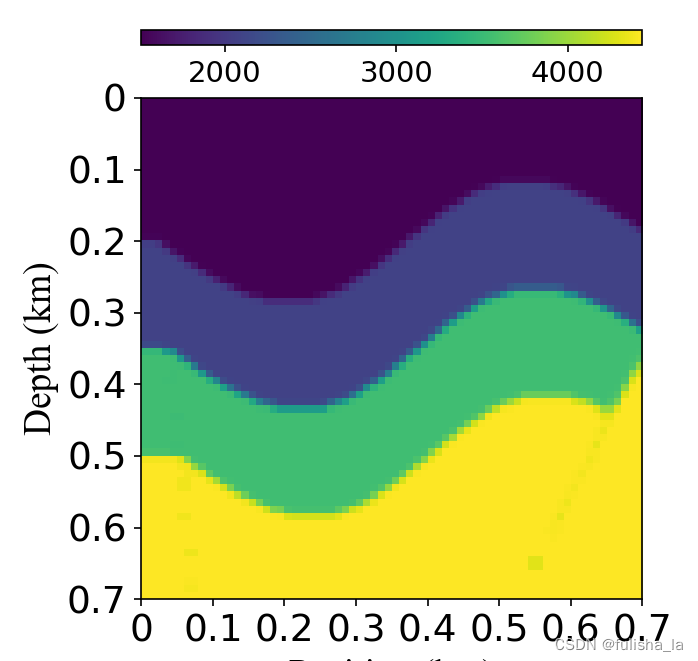
地震反演基础知识2(代码演示)
文章目录 数据集代码演示1. SEG盐真实数据2. SEG盐速度模型3. SEG盐模拟地震数据4. SEG盐模拟速度模型5. openfwi地震数据6. openfwi速度模型 数据集代码演示 1. SEG盐真实数据 # 绘制SEG盐层数据的地震图像 def pain_seg_seismic_data(para_seismic_data):Plotting seismic …...
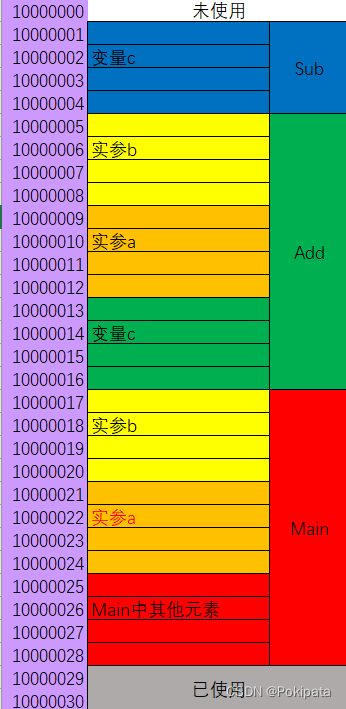
C#学习 - 方法的定义、调用、调试
方法 方法(Method)是由C/C中的函数(Function)发展而来的 //C语言 #include <stdio.h> int Add(int x, int y) {return x y; }//函数 int main(void) {int a 4;int b 2;int c Add(a, b);printf("%d %d %d\n&quo…...

『PyQt5-Qt Designer篇』| 09 Qt Designer中分割线和间隔如何使用?
09 Qt Designer中分割线和间隔如何使用? 1 间隔1.1 水平间隔1.2 垂直间隔2 分割线2.1 水平线2.2 垂直线3 保存并执行1 间隔 间隔有水平间隔和垂直间隔: 1.1 水平间隔 拖动4个按钮,并设置为水平布局: 在第一个按钮的右边添加一个水平间隔: 设置其sizeType为Fixed,宽度为20…...
基于springboot2+mybatis-plus+jsp增删改查
概述 编写简单增删改查,理解之后可以自己试着扩展,相信你也可以,加油,我自己懂了的用注释记在下面方便理解 详细 一、需求(要做什么) 基于现今最流行的技术实现增删改查demo, 便于初学者上手…...

[PHP]empty一直返回true
class Post {public function __get($key){return true;} }$post new Post(); var_dump(empty($post->a));// bool(true) PHP: 重载 - Manual 读取不可访问(protected 或 private)或不存在的属性的值时,__get() 会被调用。 当对不可访…...

[2023.09.11]: Yew的SSR中的Cargo.toml配置
由于各种原因,我最后还是打算把Yew应用的开发从csr模式转成ssr模式。没想到这里面的水还是挺深的,这里面的Cargo.toml配置包含的信息量之大,着实让我头疼了一番。 Cargo.toml的配置如下 [package] name "app" version "0.…...

HTTPS加密协议详解:HTTPS性能与优化
1、HTTPS性能损耗 前文讨论了HTTPS原理与优势:身份验证、信息加密与完整性校验等,且未对TCP和HTTP协议做任何修改。但通过增加新协议以实现更安全的通信必然需要付出代价,HTTPS协议的性能损耗主要体现如下: (1).增加延时 分析前…...

9月11日,每日信息差
今天是2023年09月11日,以下是为您准备的13条信息差 第一、微软已停止向俄罗斯提供服务,俄罗斯接下来的举动震惊世人!对此俄罗斯回应称,他们将把微软的收费版改为免费版并推广至全球 第二、我国首套海洋漂浮式温差能发电装置完成…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...

SQL进阶之旅 Day 22:批处理与游标优化
【SQL进阶之旅 Day 22】批处理与游标优化 文章简述(300字左右) 在数据库开发中,面对大量数据的处理任务时,单条SQL语句往往无法满足性能需求。本篇文章聚焦“批处理与游标优化”,深入探讨如何通过批量操作和游标技术提…...
