手撕八大排序(上)
排序的概念及其引用:
排序的概念:
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的;画图说明:
排序前A在B前面,排序后说明该排序稳定,如果排序后B在A前面则说明不稳定。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
八大排序我们一般将其分为五类,分别为:
一: 插入排序
1. 直接插入排序
2. 希尔排序
二: 选择排序
1.直接选择排序
2.堆排序
三: 交换排序
1. 冒泡排序
2. 快速排序
四: 归并排序
五:基数排序
插入排序:
直接插入排序:
基本思路:
思路:从第二个数开始,假设此数为
tmp,逐个往前进行比对,如果前数大于tmp,就将前数值赋值到tmp处,然后继续往前比对,直到找到小于或等于tmp的数(或者比对至数据首)就停止,最后将tmp的值赋值到此处就行了
动图演示:
代码:
public void insertSort(int[] array) {if (array.length == 0) {return;}for (int i = 1; i < array.length; i++) {int temp = array[i];int j = i - 1;for ( ; j >= 0 ; j--) {if (array[j] > temp) {array[j + 1] = array[j];} else {break;}}array[j + 1] = temp;}}直接插入排序总结:
1. 集合元素越接近有序,时间效率越高
2. 时间复杂度: O(N^2)
3. 空间复杂度: O(1)
4. 稳定性: 稳定
希尔排序:
前言:
既然同为插入排序,那必然是有共同点的。
希尔排序是建立在直接插入排序基础上,经过优化的插入排序。
希尔排序分为两步:
- 1、预排序,使得数据尽可能接近有序
- 2、直接插入排序,最后调用一次直接插入排序,快速的完成排序
基本思路:
思路:
预排序是通过区间划分实现的,假设当前区间为gap,那么1、1+gap*n可以分成一组,同理2、3、4都可以分,将这些组分别进行直接插入排序(数据少,效率高)。每完成一次分组排序,gap就会缩小,直到gap为1时,进行一次直接插入排序,整个希尔排序就完成了
代码如下:
public static void shellSort(int[] array) {int gap = array.length;while (gap > 1) {shell(array,gap);gap /= 2;}//整体进行插入排序shell(array,1);}public static void shell(int[] array,int gap) {for (int i = 1; i < array.length; i++) {int temp = array[i];int j = i - gap;for ( ; j >= 0 ; j-= gap) {if (array[j] > temp) {array[j + gap] = array[j];} else {break;}}array[j + gap] = temp;}}动图演示:
预排序:
直接插入排序:
希尔排序总结:
1. 希尔排序的时间复杂度要用到高数中的知识,“根据大量的数据的得到了局部的结论...”,我们直接记答案即可:O(N^1.25)
2. 空间复杂度: O(1);
我们仅仅只创建了一个gap
3. 稳定性: 不稳定;
我们在排序过程中gap会有多次的改变,不同的组别中可能会发生交换现象。
选择排序:
直接选择排序:
基本思想:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完
代码:
//选择排序public static void selectSort(int[] array) {for (int i = 0; i < array.length; i++) {int minIndex = i;for (int j = i + 1; j < array.length; j++) {if(array[j] < array[minIndex]) {minIndex = j;}}int temp = array[i];array[i] = array[minIndex];array[minIndex] = temp;}}如果像这样去遍历的话,时间复杂度为O(N^2)不算是个很优解我们可以考虑对此进行优化
优化:每次遍历选最大与最小,分别与 end 值和 begin 值交换
动图演示:

直接选择排序总结:
1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
堆排序:
我们之前也介绍过堆排序,PriorityQueue本质就是个小根堆,这里就不过多介绍了。
思路:堆排序用到了堆的知识,如果想排升序的话建大堆,因为大堆中堆顶是最大值,将堆顶值与堆低值交换后,执行向下调整,使其再次变为大堆,就这样反复交换、调整,堆排序就完成了。
/*** 堆排序* @param array 目标数组*/public static void heapSort(int[] array) {createBigHeap(array);int end = array.length - 1;while (end > 0) {swap(array,0,end);shiftDown(array,0, end);end--;}}public static void createBigHeap(int[] array) {//父下标 从倒数第二层开始int parent = (array.length - 1 -1) / 2;for (; parent > 0 ; parent-- ) {shiftDown(array,parent, array.length);}}public static void shiftDown(int[] array,int parent,int len) {int child = 2*parent + 1;while (child < len) {if (child + 1 < len && array[child] < array[child + 1]) {child++;}if (array[child] > array[parent]) {swap(array, parent, child);parent = child;child = 2 * parent + 1;} else {break;}}}private static void swap(int[] array,int i,int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}向上调整动图演示:

堆排序总结:
1. 堆排序使用堆来选数相对于直接插入排序,效率就高了很多。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
本文只是排序的上半部分,涉及的排序思想都还算简单,下一篇文章中将会介绍排序大哥:快速排序,知识点很难敬请期待吧。
相关文章:

手撕八大排序(上)
排序的概念及其引用: 排序的概念: 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 稳定性:假定在待排序的记录序列中,存在多个具有…...

clickhouse 怎么统计每天0点到10点的某个字段的数据量
比喻:统计最近一周0点到10点期间每天id的数量 日期:2023-03-23 09:02:22 日期全是这种格式 第一步先把日期转小时:先把小于10小时的查出来 toHour(card_time)<10 select toDate(t.dates) as dates,sum(t.count) as count from ( se…...

[qiankun]-图片加载问题
[qiankun]-图片加载问题开发版本图片加载报错现象描述分析解决方案base64的展示格式静态资源的展示方式取消hash的取值方式,并在主应用中添加图片设置图片的绝对路径根据环境动态设置图片的绝对路径nginx转发方式开发版本 "vue": "^3.2.45", &…...
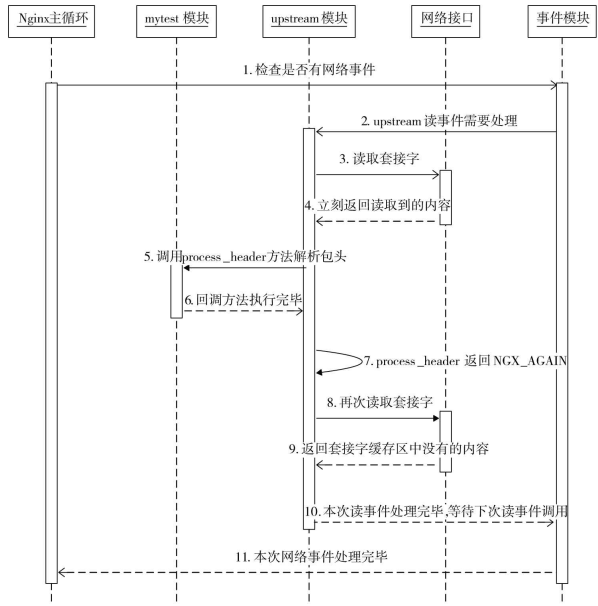
关于upstream的八种回调方法
1 creat_request调用背景:用于创建自己模板与第三方服务器的第一次连接步骤1) 在Nginx主循环(ngx_worker_process_cycle方法) 中,会定期地调用事件模块, 以检查是否有网络事件发生。2) 事件模块…...

0303泰勒公式-微分中值定理与导数的应用
文章目录1 引入2 泰勒中值定理2.1 泰勒多项式3.2 泰勒中值定理13.3 泰勒中值定理22.4 误差估计4 麦克劳林公式5 常见麦克劳林公式6 泰勒公式相关例题6.1 将函数展成指定的泰勒公式6.1.1 公式法6.1.2 间接展法(变量替换)6.2 利用泰勒公式求极限6.3 确定无…...

日常运维基础命令
commandexplainps -f -u user_name显示指定用户的进程ps aux --sort-pcpu,pmem先以cpu使用量进行排序,cpu使 用一样,以内存使用率排序ps -ef --forest显示ACLII进程数ps --ppid 28208显示父进程的子进程ps -p 14447 -L显示进程的线程ps -e -o pid&#x…...
人员行为识别系统 TensorFlow
人员行为识别系统人员行为识别系统通过TensorFlow深度学习技术,人员行为识别算法对画面中区域人员不按要求穿戴、违规抽烟打电话、睡岗离岗以及作业流程不规范实时分析预警,发现违规行为立即抓拍告警。深度学习应用到实际问题中,一个非常棘手…...

ES-倒排索引BKD原理skiplist
1.Elasticsearch数据存储结构FST、skiplist、BKD-tree、LSM-tree Elasticsearch数据结构存储流程_善思的博客-CSDN博客_elasticsearch 数据结构 number?keyword?傻傻分不清楚 - Elastic 中文社区 ElasticSearch实战(六)-Skip List 跳表算法…...
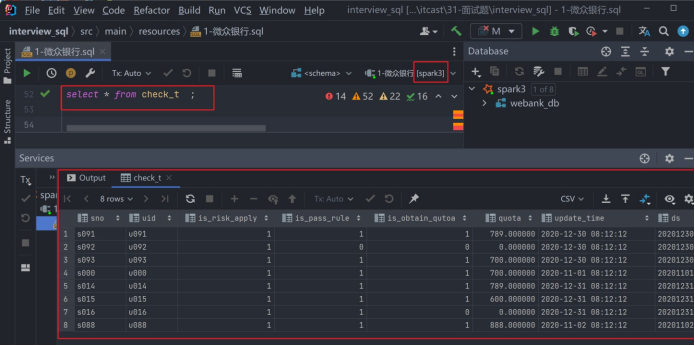
每天一道大厂SQL题【Day12】微众银行真题实战(二)
每天一道大厂SQL题【Day12】微众银行真题实战(二) 大家好,我是Maynor。相信大家和我一样,都有一个大厂梦,作为一名资深大数据选手,深知SQL重要性,接下来我准备用100天时间,基于大数据岗面试中的经典SQL题&…...
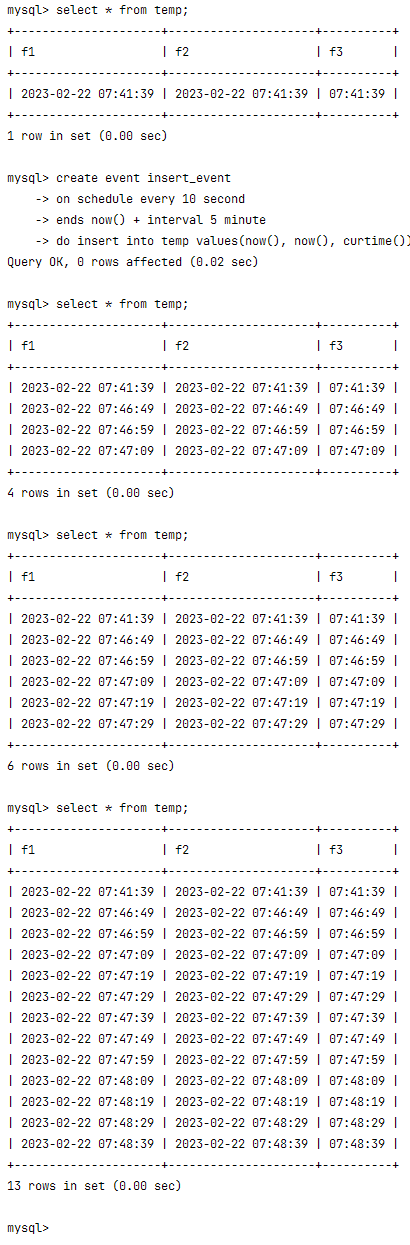
带您了解TiDB MySQL数据库中关于日期、时间的坑
带您了解TiDB & MySQL数据库中关于日期、时间的坑时间的基础知识什么是时间计算时间的几种方法世界时(UT)协调世界时(UTC)国际原子时(TAI)时区的概念中国所在的时区操作系统的时区datetimedatectl数据库…...

【华为OD机试模拟题】用 C++ 实现 - 求字符串中所有整数的最小和
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...
harbor 仓库迁移升级
harbor 仓库迁移升级 harbor仓库安装数据传输仓库切换版本 v1.8.0 v2.3.5 harbor仓库安装 环境准备:安装docker详见:docker 的介绍和部署,并下载docker-compose详见:docker 三剑客compose。 现有支持的安装harbor仓库的方式有两…...

评论功能设计思路~
文章目录 评论功能设计框架1、定义2、目标3、动机4、评论类别**5、评论互动****6、评论区展示结构****6.1 主题式****6.2 平铺式****6.3 盖楼式****7、评论排序机制****8、评论加载形式****9、其他**结语评论功能设计框架 1、定义 评论是指针对于事物进行主观或客观的自我印象…...

算法训练营 day52 动态规划 买卖股票的最佳时机系列1
算法训练营 day52 动态规划 买卖股票的最佳时机系列1 买卖股票的最佳时机 121. 买卖股票的最佳时机 - 力扣(LeetCode) 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票…...

3.基于分割的文本检测算法--DBNet++
文章目录1.概况2.DBNet中的主要方法2.1 网络结构2.2 适应特征图融合模块(Adaptive Scale Fusion Module, ASF)3.ASF模块的源码实现参考资料欢迎访问个人网络日志🌹🌹知行空间🌹🌹 1.概况 2022年02月份论文:Real-Time S…...

IOS打包、SDK接入记录等
IOS打包、SDK接入记录等 Mac上安装HCLR路径 /Applications/Unity/Hub/Editor/2019.4.40f1c1/Unity.app/Contents/il2cpp HCLR 指定4.40是要Unity启动打开的il2cpp,否则HCLR Installer他会报找不到MonoBleedingEdge Mac删除证书 只能点击钥匙串做上角的登录后&…...
【C++】类与对象(引入)
目录 前言 类的引入 类的定义 封装与访问限定符 封装 访问限定符 类的实例化 类的大小 this指针 特性 前言 🎶我们都知道,C语言是面向过程的编程,而C是面向对象的编程,更多体现在编程的关注点上。 🎶就拿洗…...
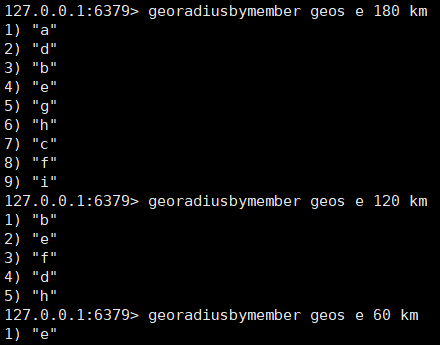
Redis 高级数据类型
文章目录一、Bitmaps:属性状态统计二、HyperLogLog:基数统计三、GEO:地理位置信息计算提示:以下是本篇文章正文内容,Redis系列学习将会持续更新 一、Bitmaps:属性状态统计 Bitmaps类型: 统计一…...

Java8 新特性-函数式接口
什么是函数式接口 先来看看传统的创建线程是怎么写的 Thread t1 new Thread(new Runnable() {Overridepublic void run() {System.out.println("t1");} }); t1.start();再来看看使用了函数式接口是怎么写的 Thread t2 new Thread(() -> System.out.println(&…...
这套软件测试试卷能打90分,直接入职字节吧
目录 一.填空 二、 判断题(正确的√,错误的╳)共10分,每小题1分 三、数据库部分:(共15分) 四、设计题。本题共 1 小题,满分 20分 一.填空 1、 系…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...




