【数据结构】队列知识点总结--定义;基本操作;队列的顺序实现;链式存储;双端队列;循环队列
欢迎各位看官^_^
目录
1.队列的定义
2.队列的基本操作
2.1初始化队列
2.2判断队列是否为空
2.3判断队列是否已满
2.4入队
2.5出队
2.6完整代码
3.队列的顺序实现
4.队列的链式存储
5.双端队列
6.循环队列
1.队列的定义
队列(Queue)是一种先进先出(First In First Out,FIFO)的线性数据结构,它只允许在队尾添加元素,在队头删除元素,不支持随机访问。队列常用的操作有入队(enqueue)、出队(dequeue)、队列长度(size)、队列是否为空(empty)等。队列可以用来实现很多算法,如广度优先搜索算法(BFS)和消息传递等。
2.队列的基本操作
2.1初始化队列
可以使用数组或链表来实现队列。对于数组,我们可以定义一个数组和两个指针(front和rear)来表示队列。对于链表,我们可以创建一个链表,并定义头节点指针和尾节点指针。队列是一种线性数据结构,可以用数组或链表来实现。
以下是用数组实现队列的C语言代码示例:
#include <stdio.h>#define MAX_SIZE 100int queue[MAX_SIZE];
int front = 0, rear = -1;void enqueue(int data) {if (rear == MAX_SIZE - 1) {printf("Queue overflow\n");} else {rear++;queue[rear] = data;}
}int dequeue() {if (front > rear) {printf("Queue underflow\n");return -1;} else {int data = queue[front];front++;return data;}
}int main() {enqueue(10);enqueue(20);enqueue(30);printf("%d ", dequeue());printf("%d ", dequeue());printf("%d ", dequeue());printf("%d ", dequeue());return 0;
}
上述代码中,`queue`为数组,`front`和`rear`分别表示队列的前后指针,初始化为`0`和`-1`。`enqueue`函数用于向队列中添加元素,先判断队列是否已满,若未满则将数据存入队列尾部。`dequeue`函数用于弹出队列头部元素,先判断队列是否为空,若非空则返回队列头部元素并将`front`指针后移一位。在`main`函数中,先将元素10、20、30添加到队列中,然后依次弹出队列头部元素并输出。
2.2判断队列是否为空
如果队列为空,则front和rear指向同一个位置。
// 判断队列是否为空
int is_empty() {return front == rear;
}2.3判断队列是否已满
如果队列已满,则rear指向的下一个位置就是front(因为它是循环队列)。
// 判断队列是否已满
int is_full() {return (rear + 1) % MAX_SIZE == front;
}
2.4入队
当队列不满时,我们将元素插入队列的rear位置,并将rear指针后移。
// 入队
void enqueue(int data) {if (is_full()) {printf("Queue is full.\n");return;}queue[rear] = data;rear = (rear + 1) % MAX_SIZE;
}
2.5出队
当队列不为空时,我们将front指向的元素从队列中删除,并将front指针后移。
// 出队
int dequeue() {if (is_empty()) {printf("Queue is empty.\n");return -1;}int data = queue[front];front = (front + 1) % MAX_SIZE;return data;
}
2.6完整代码
#include <stdio.h>
#define MAX_SIZE 10 // 定义队列的最大容量为10int queue[MAX_SIZE]; // 定义数组队列
int front = 0, rear = 0; // front指向队首,rear指向队尾的下一个位置// 判断队列是否为空
int is_empty() {return front == rear;
}// 判断队列是否已满
int is_full() {return (rear + 1) % MAX_SIZE == front;
}// 入队
void enqueue(int data) {if (is_full()) {printf("Queue is full.\n");return;}queue[rear] = data;rear = (rear + 1) % MAX_SIZE;
}// 出队
int dequeue() {if (is_empty()) {printf("Queue is empty.\n");return -1;}int data = queue[front];front = (front + 1) % MAX_SIZE;return data;
}int main() {enqueue(1);enqueue(2);enqueue(3);printf("%d\n", dequeue());printf("%d\n", dequeue());enqueue(4);printf("%d\n", dequeue());printf("%d\n", dequeue());return 0;
}
注意:这是一个循环队列,在计算rear的位置时需要使用取模运算。这是因为数组的最后一个位置后面没有下一个位置,我们需要将rear回到数组的开头位置。
3.队列的顺序实现
C语言队列的顺序实现可以使用数组来实现。实现思路如下:
- 定义一个数组和队列头尾指针。
- 队列头指针指向队列的第一个元素,队列尾指针指向队列的最后一个元素。
- 入队操作时,先判断队列是否已满,如果已满则提示队列已满,否则将元素加入到队列尾部,并更新队列尾指针。
- 出队操作时,先判断队列是否为空,如果为空则提示队列为空,否则将队列头部的元素出队,并更新队列头指针。
- 获取队列头元素时,先判断队列是否为空,如果为空则提示队列为空,否则返回队列头的元素。
以下是C语言队列的顺序实现示例代码:
#include <stdio.h>
#define MAX_SIZE 100// 定义队列结构体
typedef struct {int data[MAX_SIZE]; // 存储队列的数组int front; // 队列头指针int rear; // 队列尾指针
} Queue;// 初始化队列
void initQueue(Queue *q) {q->front = q->rear = 0;
}// 入队
void enqueue(Queue *q, int x) {if ((q->rear + 1) % MAX_SIZE == q->front) {printf("Queue is full.\n");} else {q->data[q->rear] = x;q->rear = (q->rear + 1) % MAX_SIZE;}
}// 出队
void dequeue(Queue *q) {if (q->front == q->rear) {printf("Queue is empty.\n");} else {q->front = (q->front + 1) % MAX_SIZE;}
}// 获取队列头元素
int front(Queue *q) {if (q->front == q->rear) {printf("Queue is empty.\n");return -1;} else {return q->data[q->front];}
}// 判断队列是否为空
int isEmpty(Queue *q) {return q->front == q->rear;
}int main() {Queue q;initQueue(&q);// 入队enqueue(&q, 1);enqueue(&q, 2);enqueue(&q, 3);// 获取队列头元素printf("Front of queue: %d\n", front(&q));// 出队dequeue(&q);// 获取队列头元素printf("Front of queue: %d\n", front(&q));return 0;
}
4.队列的链式存储
队列和链表的关系:队列和链表是两种不同的数据结构,但是在实现队列时可以使用链表来表示。队列是一种先进先出(First In First Out,FIFO)的数据结构,可以理解为是一条通道,从一端(队尾)加入数据,从另一端(队头)取出数据。而链表是一种动态数据结构,由节点之间的指针连接而成。每个节点包含一个数据元素和一个指向下一个节点的指针。在使用链表实现队列时,可以将链表的头作为队列的队头,将链表的尾作为队列的队尾,使用链表的头插法或尾插法对队列进行入队操作,使用链表的尾删除或头删除对队列进行出队操作。因此,可以说队列和链表有一定的关系,但二者仍然是不同的数据结构。
队列的链式存储是使用链表来实现队列的存储结构。队列的链式存储结构可以分为单向链表和双向链表两种。
单向链表的存储结构是每个节点包含一个数据元素和一个指向下一个节点的指针。队列的头指针指向链表的头节点,队列的尾指针指向链表的尾节点。入队操作将元素添加到尾节点之后,出队操作则删除头节点。
双向链表的存储结构是每个节点包含一个数据元素、一个指向前一个节点的指针和一个指向下一个节点的指针。队列的头指针指向链表头部,队列的尾指针指向链表尾部。入队操作将元素添加到尾节点之后,出队操作则删除头节点。
链式存储相比于顺序存储的优势在于可以更灵活地插入和删除元素,但是在访问元素时需要通过指针遍历链表,效率较低。
链式存储结构的队列通常包含一个头结点和一个尾结点,其中头结点指向队列的头部,尾结点指向队列的尾部。每个结点都包含一个数据域和一个指针域,指针域指向下一个结点。
以下是C语言实现队列的链式存储的示例代码:
#include <stdio.h>
#include <stdlib.h>// 队列结点定义
typedef struct queue_node{int data; // 数据域struct queue_node *next; // 指针域
} queue_node;// 队列定义
typedef struct {queue_node *front; // 队列头指针queue_node *rear; // 队列尾指针
} queue;// 初始化队列
void init_queue(queue *q)
{// 分配头结点q->front = q->rear = (queue_node *)malloc(sizeof(queue_node));if (!q->front) {printf("Memory allocation failed.\n");exit(-1);}q->front->next = NULL;
}// 判断队列是否为空
int is_empty(queue *q)
{return q->front == q->rear;
}// 入队
void enqueue(queue *q, int data)
{queue_node *new_node = (queue_node *)malloc(sizeof(queue_node));if (!new_node) {printf("Memory allocation failed.\n");exit(-1);}new_node->data = data;new_node->next = NULL;q->rear->next = new_node;q->rear = new_node;
}// 出队
int dequeue(queue *q)
{if (is_empty(q)) {printf("Queue is empty.\n");exit(-1);}queue_node *p = q->front->next;int data = p->data;q->front->next = p->next;if (q->rear == p) {q->rear = q->front;}free(p);return data;
}// 输出队列中元素
void print_queue(queue *q)
{queue_node *p = q->front->next;while (p) {printf("%d ", p->data);p = p->next;}printf("\n");
}int main()
{queue q;init_queue(&q);for (int i = 1; i <= 5; i++) {enqueue(&q, i);}print_queue(&q);dequeue(&q);print_queue(&q);return 0;
}
5.双端队列
双端队列(deque,全名double-ended queue)是一种具有队列和栈的性质的数据结构,即两端都可以进行插入和删除操作。
双端队列有两个端点:一个是“前端”(front),可以进行“出队”操作;另一个是“后端”(rear),可以进行“入队”操作。因此,双端队列支持的操作包括入队、出队、队头入队、队尾入队、队头出队、队尾出队等。
与单端队列相比,双端队列的优势在于可以自由地从两端添加或删除元素,更加灵活、方便地实现某些算法和数据结构。例如,在实现图遍历算法中,使用双端队列可以使得遍历的顺序更加合理,减少搜索的时间和空间复杂度。
另外,双端队列支持一些其他的操作,如获取队列长度、获取队头/尾元素等。
以下是C语言实现双端队列的代码:
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>// 双端队列节点结构体
typedef struct DequeNode {int val;struct DequeNode* next;struct DequeNode* prev;
} DequeNode;// 双端队列结构体
typedef struct Deque {DequeNode* front; // 队头指针DequeNode* rear; // 队尾指针int size; // 队列元素个数
} Deque;// 初始化双端队列
void initDeque(Deque* deque) {deque->front = NULL;deque->rear = NULL;deque->size = 0;
}// 判断双端队列是否为空
bool isEmptyDeque(Deque* deque) {return deque->size == 0;
}// 获取双端队列的长度
int sizeDeque(Deque* deque) {return deque->size;
}// 获取双端队列队头元素
int frontDeque(Deque* deque) {return deque->front->val;
}// 获取双端队列队尾元素
int rearDeque(Deque* deque) {return deque->rear->val;
}// 在双端队列前端插入元素
void addFrontDeque(Deque* deque, int val) {DequeNode* new_node = (DequeNode*)malloc(sizeof(DequeNode));new_node->val = val;new_node->next = deque->front;new_node->prev = NULL;if (deque->front != NULL) {deque->front->prev = new_node;}deque->front = new_node;if (deque->rear == NULL) {deque->rear = new_node;}deque->size++;
}// 在双端队列后端插入元素
void addRearDeque(Deque* deque, int val) {DequeNode* new_node = (DequeNode*)malloc(sizeof(DequeNode));new_node->val = val;new_node->next = NULL;new_node->prev = deque->rear;if (deque->rear != NULL) {deque->rear->next = new_node;}deque->rear = new_node;if (deque->front == NULL) {deque->front = new_node;}deque->size++;
}// 在双端队列前端删除元素
void removeFrontDeque(Deque* deque) {if (deque->front == NULL) {return;}DequeNode* temp = deque->front;deque->front = deque->front->next;if (deque->front != NULL) {deque->front->prev = NULL;} else {deque->rear = NULL;}free(temp);deque->size--;
}// 在双端队列后端删除元素
void removeRearDeque(Deque* deque) {if (deque->rear == NULL) {return;}DequeNode* temp = deque->rear;deque->rear = deque->rear->prev;if (deque->rear != NULL) {deque->rear->next = NULL;} else {deque->front = NULL;}free(temp);deque->size--;
}// 测试
int main() {Deque deque;initDeque(&deque);addFrontDeque(&deque, 1);addRearDeque(&deque, 2);addFrontDeque(&deque, 3);addRearDeque(&deque, 4);while (!isEmptyDeque(&deque)) {printf("%d ", frontDeque(&deque));removeFrontDeque(&deque);}printf("\n");return 0;
}
6.循环队列
循环队列是一种环形数据结构,它允许在一端添加数据元素,同时在另一端删除数据元素。与线性队列不同的是,在循环队列中,队头和队尾是可以相互穿越的。这意味着队列的末尾可以连接到队列的开始,形成一个环。这样,可以使用有限的空间,存储无限数量的数据元素。
循环队列通常使用数组来实现。它有一个前后指针,称为队头和队尾。入队操作时,将新元素加入队尾,并将队尾指针向后移动。出队操作时,将队头元素删除,并将队头指针向后移动。当队列满时,新元素无法插入,即使队列前面有空位置。当队列为空时,无法删除元素。
循环队列的主要优点是可以避免队列的前面空出大量空间,同时保证队列的顺序性和完整性。缺点是在实现时需要注意控制队列满和空的情况,以及指针的计算。
循环队列是一种特殊的队列,其队尾指针指向数组的末尾后会回到数组的开头,实现队列的循环利用。下面是C语言实现循环队列的示例代码:
#include <stdio.h>
#include <stdlib.h>#define QUEUE_MAX_SIZE 5 // 队列的最大容量typedef struct {int* data; // 队列数据存储的位置int front; // 队首指针int rear; // 队尾指针
} Queue;// 初始化队列
void InitQueue(Queue* q) {q->data = (int*)malloc(QUEUE_MAX_SIZE * sizeof(int)); // 分配队列空间q->front = q->rear = 0; // 初始化队首和队尾指针
}// 判断队列是否为空
int IsEmpty(Queue* q) {return q->front == q->rear;
}// 判断队列是否已满
int IsFull(Queue* q) {return (q->rear + 1) % QUEUE_MAX_SIZE == q->front;
}// 入队操作
int EnQueue(Queue* q, int value) {if (IsFull(q)) {return 0; // 队列已满,无法入队}q->data[q->rear] = value; // 将数据存入队列q->rear = (q->rear + 1) % QUEUE_MAX_SIZE; // 队尾指针后移return 1; // 入队成功
}// 出队操作
int DeQueue(Queue* q, int* value) {if (IsEmpty(q)) {return 0; // 队列为空,无法出队}*value = q->data[q->front]; // 取出队首数据q->front = (q->front + 1) % QUEUE_MAX_SIZE; // 队首指针后移return 1; // 出队成功
}// 获取队首元素
int GetFront(Queue* q, int* value) {if (IsEmpty(q)) {return 0; // 队列为空,无法获取队首元素}*value = q->data[q->front]; // 获取队首元素return 1; // 获取成功
}// 获取队列长度
int GetLength(Queue* q) {return (q->rear - q->front + QUEUE_MAX_SIZE) % QUEUE_MAX_SIZE;
}// 输出队列中的所有元素
void PrintQueue(Queue* q) {int i, len = GetLength(q);for (i = 0; i < len; i++) {int value;DeQueue(q, &value);printf("%d ", value);EnQueue(q, value);}printf("\n");
}// 测试代码
int main() {Queue q;InitQueue(&q);EnQueue(&q, 1);EnQueue(&q, 2);EnQueue(&q, 3);EnQueue(&q, 4);EnQueue(&q, 5);printf("Queue length: %d\n", GetLength(&q)); // 5printf("Queue content: ");PrintQueue(&q); // 1 2 3 4 5int value;DeQueue(&q, &value);printf("DeQueue value: %d\n", value); // 1printf("Queue content: ");PrintQueue(&q); // 2 3 4 5EnQueue(&q 在上面的代码中,我们实现了循环队列的初始化、判断是否为空或已满、入队、出队、获取队首元素、获取队列长度和输出队列中的所有元素等操作。我们可以通过这些操作对循环队列进行基本的操作。
🤞❤️🤞❤️🤞❤️栈的知识点总结就到这里啦,如果对博文还满意的话,劳烦各位看官动动“发财的小手”留下您对博文的赞和对博主的关注吧🤞❤️🤞❤️🤞❤️

相关文章:

【数据结构】队列知识点总结--定义;基本操作;队列的顺序实现;链式存储;双端队列;循环队列
欢迎各位看官^_^ 目录 1.队列的定义 2.队列的基本操作 2.1初始化队列 2.2判断队列是否为空 2.3判断队列是否已满 2.4入队 2.5出队 2.6完整代码 3.队列的顺序实现 4.队列的链式存储 5.双端队列 6.循环队列 1.队列的定义 队列(Queue)是一种先…...

嵌入式学习之链表
对于链表,要重点掌握链表和数组区别和实现,链表静态添加和动态遍历,链表中pointpoint-next,链表节点个数的查找,以及链表从指定节点后方插入新节点的知识。...
静态代理和动态代理笔记
总体分为: 1.静态代理: 代理类和被代理类需要实现同一个接口.在代理类中初始化被代理类对象.在代理类的方法中调 用被代理类的方法.可以选择性的在该方法执行前后增加功能或者控制访问 2.动态代理: 在程序执行过程中,实用JDK的反射机制,创建代理对象,并动态的指定要…...

[SM6225][Android13]user版本默认允许root和remount
开发平台基本信息 芯片: 高通SM6225版本: Android 13kernel: msm-5.15 问题描述 刚刚从Framework踏入性能的小殿堂,User版本默认是不会开启root权限的,而且一般调试需要设置一下CPU GPU DDR performance模式或者修改一些schedule util等调核调频节点去…...

pyinstaller打包exe,使用wexpect的问题
参考github首先打包wexpect 1.进入wexpect目录执行 pyinstaller __main__.py -n wexpect 会生成dist文件夹 2.python代码A.py中使用wexpect,注意wexpect.spawn前后必须按照下面添加代码 import sys,os,wexpect #spawn前 real_executable sys.executable try:if sy…...
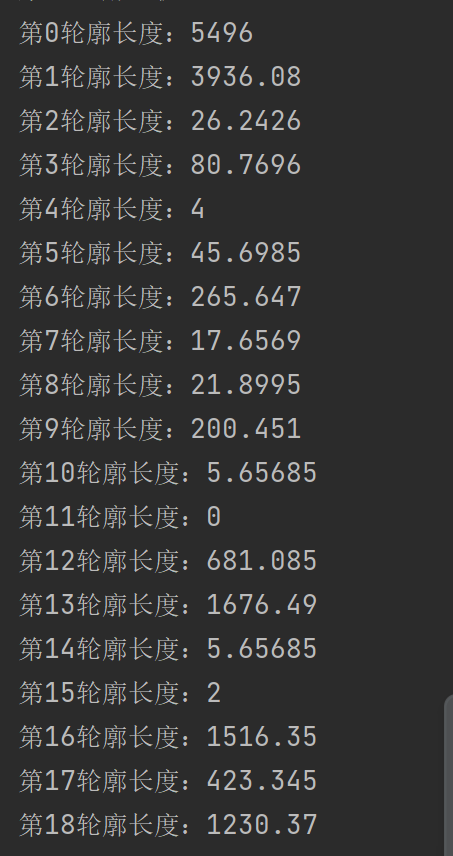
OpenCV(三十三):计算轮廓面积与轮廓长度
1.介绍轮廓面积与轮廓长度 轮廓面积(Contour Area)是指轮廓所包围的区域的总面积。通常情况下,轮廓面积的单位是像素的平方。 轮廓长度(Contour Length)又称周长(Perimeter),表示轮廓…...
9.11作业
实现一个对数组求和的函数,数组通过实参传递给函数 sum0 arr(11 22 33 44 55) Sum() {for i in ${arr[*]}do$((sumi))donereturn $sum } Sum ${arr[*]} var$? echo $var写一个函数,输出当前用户的uid和gid,并使用变量接收结果 Sum() {aid -…...

AI伦理与未来社会:探讨人工智能的道德挑战与机会
引言 引出AI伦理和社会影响的主题,强调AI的快速发展和广泛应用。 概述博客的主要内容:探讨AI的伦理挑战以及它对社会的影响。 第一部分:AI的伦理挑战 算法偏见: 解释什么是算法偏见,以及它为何在AI中成为一个重要问题。…...

Android窗口层级(Window Type)分析
前言 Android的窗口Window分为三种类型: 应用Window,比如Activity、Dialog;子Window,比如PopupWindow;系统Window,比如Toast、系统状态栏、导航栏等等。 应用Window的Z-Ordered最低,就是在系…...

微信小程序基础加强总结
本篇文章给大家带来了关于微信小程序的相关问题,其中主要介绍了一些基础内容,包括了自定义组件、样式隔离、数据、方法和属性等等内容,下面一起来看一下,希望对大家有帮助。 1、自定义组件 1.1、创建组件 在项目的根目录中&…...
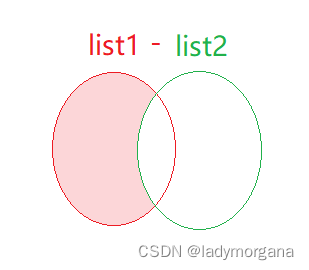
【JAVA - List】差集removeAll() 四种方法实现与优化
一、场景: 二、结论: 1. 四种方法耗时 三、代码: 一、场景: 求差集 List1 - Lsit2 二、结论: 1. 四种方法耗时 初始条件方法名方法思路耗时 List1.size319418 List2.size284900 List..removeAll(Lsit2)1036987ms…...
sql注入基本概念
死在山野的风里,活在自由的梦里 sql注入基本概念 MYSQL基本语法union合并查询2个特性:order by 排序三个重要的信息 Sql Server MYSQL 基本语法 登录 mysql -h ip -u user -p pass基本操作 show databases; 查看数据库crea…...

AIGC系列:1.chatgpt可以用来做哪些事情?
上图的意思:神器轩辕剑 那么,在现在AI盛行的信息时代, 你是否知道如何获得和利用ChatGPT这一把轩辕剑来提升你的攻击力和生存能力呢? 故事 程序员小张: 刚毕业,参加工作1年左右,日常工作是C…...
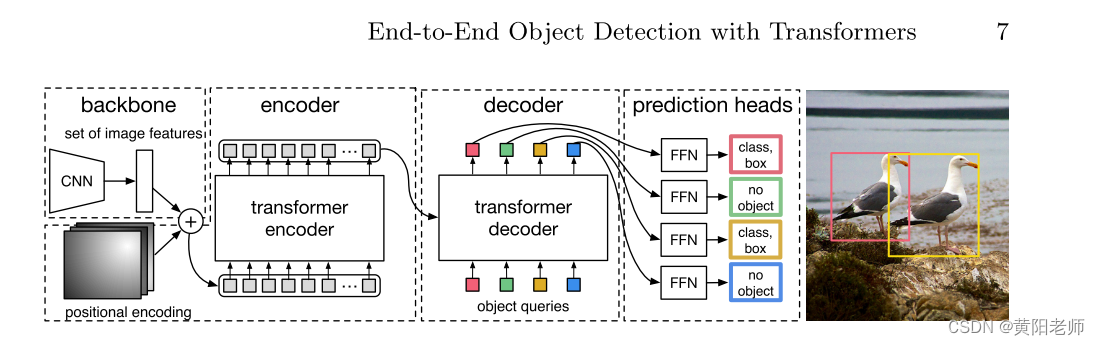
End-to-End Object Detection with Transformers(论文解析)
End-to-End Object Detection with Transformers 摘要介绍相关工作2.1 集合预测2.2 transformer和并行解码2.3 目标检测 3 DETR模型3.1 目标检测集设置预测损失3.2 DETR架构 摘要 我们提出了一种将目标检测视为直接集合预测问题的新方法。我们的方法简化了检测流程,…...
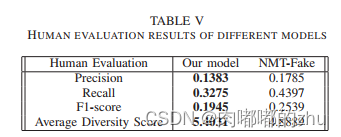
生成多样、真实的评论(2019 IEEE International Conference on Big Data )
论文题目(Title):Learning to Generate Diverse and Authentic Reviews via an Encoder-Decoder Model with Transformer and GRU 研究问题(Question):评论生成,由上下文评论->生成评论 研…...

项目中应该使用nginx还是拦截器来封禁IP
项目中应该使用nginx还是拦截器来封禁IP 在项目中,使用 Nginx 或拦截器(例如 Spring Interceptor)来封禁 IP 地址都是可行的方法,具体选择取决于你的需求和项目架构。 Nginx 是一种高性能的 Web 服务器和反向代理服务器…...
SMB 协议详解之-NTLM身份认证
前面的文章说明了SMB协议交互的过程,在SMB交互的Session Setup Request/Response会对请求者的身份进行验证,这其中涉及到两个主要的协议NTLM以及Kerberos,本文将对NTLM协议进行详细的说明。 什么是NTLM NTLM是 NT LAN Manager (NTLM) Authentication Protocol 的缩写,主要…...
day34 Set
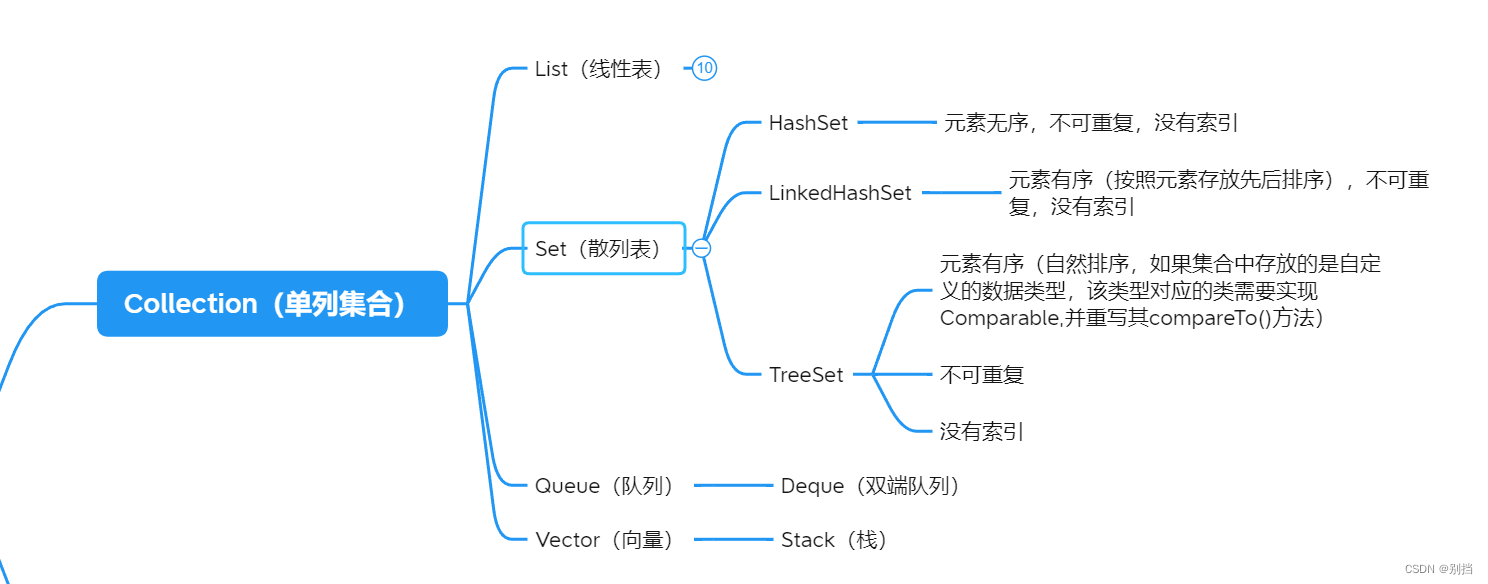
概述 Set也是集合Collection接口的子接口 Set也是集合Collection接口的子接口 特点:不保证元素有顺序,数组元素不可以重复 HashSet: 底层是基于HashMap的。元素是无序的。元素不可重复,去重机制是依据hashCode()和equals()方法 LinkedHas…...
数据库_之常用API的使用
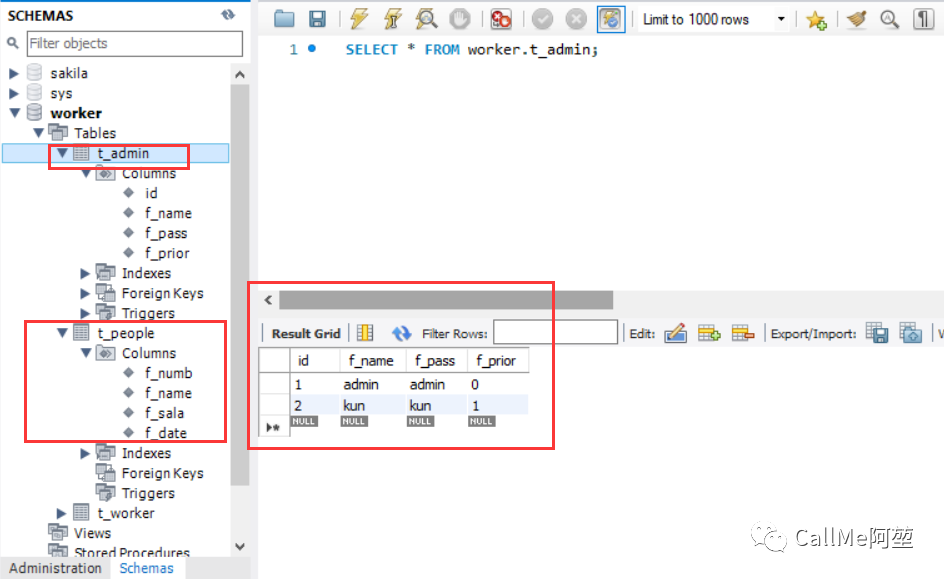
数据库_之电商API MySQL C API 使用(基本函数) Mysql C API函数详解 MySQL的常用API 一个常用的程序调用MySQL数据库的时候通常都会调用以下API,下面来逐个分析. mysql_init() //函数原型 MYSQL *STDCALL mysql_init(MYSQL *mysql);这个API主要是用来分…...

CTreeCtrl自绘
CSWTreeCtrl.h) #pragma once#define _OWNER_DRAWN_TREE // 自绘CTreeCtrl,可支持背景图片显示功能class CSWTreeCtrl : public CTreeCtrl {DECLARE_DYNAMIC(CSWTreeCtrl)// 成员私有结构定义// 构造/析构函数 public:CSWTreeCtrl();virtual ~CSWTreeC…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

