overleaf中latex语法总结
α和bata
$\alpha$ $\beta$
上标和下标同时使用
$A_{IJ}^{I+J}$\\ %上标^下标_多个使用{}
行内公式
\noindent $a+b=c$\\ %行内公式
\documentclass{article}
\usepackage[utf8]{inputenc}
\usepackage[namelimits]{amsmath} %数学公式
\usepackage{amssymb} %数学公式
\usepackage{amsfonts} %数学字体
\usepackage{mathrsfs} %数学花体
\begin{document}\[a+b=c\] %行间公式\begin{equation}
a+b=c %自动编号
\end{equation}log: $\log_3 5$ sin: $\sin({x}^2)$\\ %log sin等
$\alpha$ $\nu$ $\beta$ $\gamma$ $\xi$ $\delta$ $\pi$ $\epsilon$\\%希腊字母
$\rho$ $\zeta$ $\sigma$ $\eta$ $\tau$ $\theta$ $\upsilon$ $\iota$\\
$\phi$ $\kappa$ $\chi$ $\lambda$ $\psi$ $\mu$\\
$3\times4=12$\\ %乘法
$\frac{12}{4}$\\ %分数
$\sqrt[3]{\frac{1}{x}}$\\ %开方
$\sqrt{\frac{1}{x}}$\\ %开方
$\max \limits_{1<x<100}f(x)$\\ %max min
\[\min_{x \in R} f(x)\] % 行间所有的下标都会在下面
$\underset{0\leq j \leq k-1}{\arg\min}$\\% 符号在下面,以下需要数学公式包支持
\[\underset{0\leq j \leq k-1}{\arg\min}\]
$\sum_{\substack{0<i<n \\ 0<j<n}} A_{ij}$% 符号在下面换行
\[\sum_{\substack{0<i<n \\ 0<j<n}} A_{ij}\]\\
$\underrightarrow{A}$\\% 箭头
$A\xleftarrow{n=0}B\xrightarrow[T]{n>0}C$\\
$a\cup b$,$a\cap b,\overline{U}$\\%
$\emptyset,\partial,\int,\iint,\iiint,\oint$\\%
$\triangleq,\sum,\prod,\neq,\leq,\geq$\\%
$a \in b,a \notin b$\\%
$\forall,\exists,\infty,\sim,\to,\left\{ ... \right\}$\\% \end{document}相关文章:

overleaf中latex语法总结
α和bata $\alpha$ $\beta$上标和下标同时使用 $A_{IJ}^{IJ}$\\ %上标^下标_多个使用{}行内公式 \noindent $abc$\\ %行内公式\documentclass{article} \usepackage[utf8]{inputenc} \usepackage[namelimits]{amsmath} %数学公式 \usepackage{amssymb} %数学公式…...
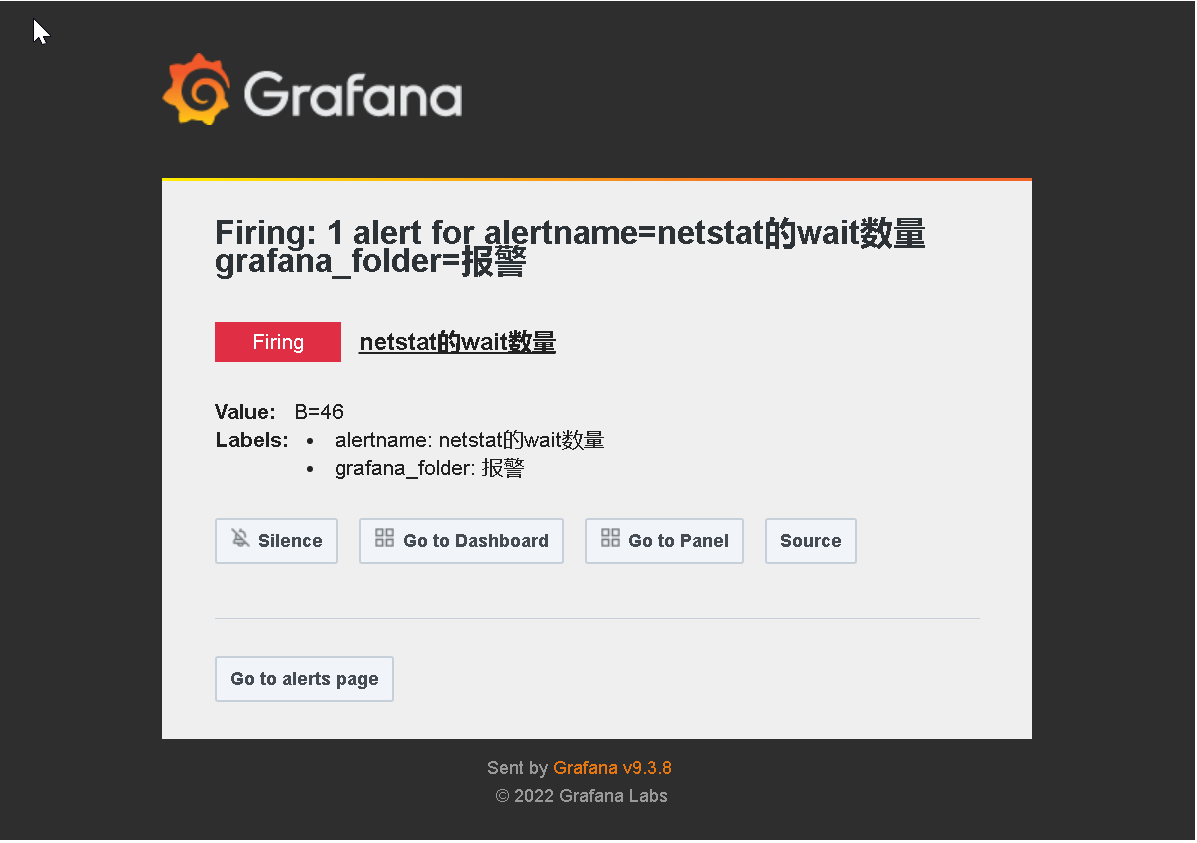
Grafana配置邮件告警
1、创建一个监控图 2、grafana邮件配置 vim /etc/grafana/grafana.ini [smtp] enabled true host smtp.163.com:465 user qinziteng05163.com password xxxxx # 授权码 from_address qinziteng05163.com from_name Grafanasystemctl restart grafana-serv…...

setup中的nextTick函数
await nextTick() 是 Vue 3 的一个异步函数,用于等待 DOM 更新完成后执行回调函数, 它在 setup 函数中非常有用,可以确保在对 DOM 进行操作之前,先等待 Vue 完成相关的 DOM 更新。 下面是一个示例,演示了 await nextT…...
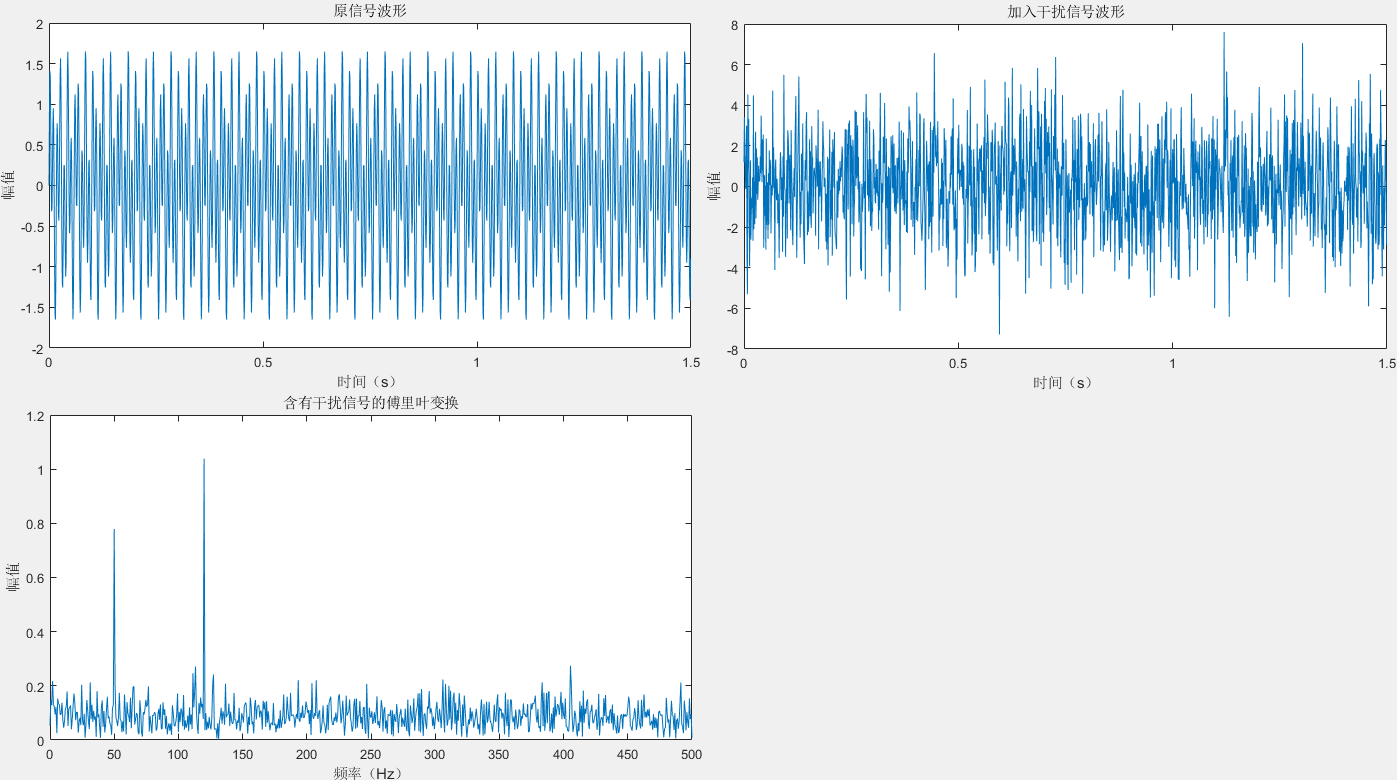
Matlab信号处理3:fft(快速傅里叶变换)标准使用方式
Fs 1000; % 采样频率 T 1/Fs; % 采样周期:0.001s L 1500; % 信号长度 t (0:L-1)*T; % 时间向量. 时间向量从0开始递增,0s~1.499sS 0.7*sin(2*pi*50*t) sin(2*pi*120*t); % 模拟原信号 X S 2*randn(size(t)); …...

Python|合并两个字典的几种方法
在Python中,有多种方法可以通过使用各种函数和构造函数来合并字典。在本文中,我们将讨论一些合并字典的方法。 1. 使用方法update() 通过使用Python中的update()方法,可以将一个列表合并到另一个列表中。但是在这种情况下,第二个…...

ElementUI浅尝辄止24:Message 消息提示
常用于主动操作后的反馈提示。与 Notification 的区别是后者更多用于系统级通知的被动提醒。 1.如何使用? Message 在配置上与 Notification 非常类似,所以部分 options 在此不做详尽解释,可以结合 Notification 的文档理解它们。Element 注…...

让照片动起来的软件,轻松制作照片动效
随着社交媒体的日益普及,我们对于照片的要求也越来越高。普通的照片已经不能满足我们的需求,我们希望照片更加生动有趣。照片动效便应运而生,它可以让照片动起来,吸引更多的注意力,让照片更加生动有趣。 照片动效制作起…...

【图解RabbitMQ-7】图解RabbitMQ五种队列模型(简单模型、工作模型、发布订阅模型、路由模型、主题模型)及代码实现
🧑💻作者名称:DaenCode 🎤作者简介:CSDN实力新星,后端开发两年经验,曾担任甲方技术代表,业余独自创办智源恩创网络科技工作室。会点点Java相关技术栈、帆软报表、低代码平台快速开…...

Linux命令200例:write用于向特定用户或特定终端发送信息
🏆作者简介,黑夜开发者,CSDN领军人物,全栈领域优质创作者✌。CSDN专家博主,阿里云社区专家博主,2023年6月csdn上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师࿰…...
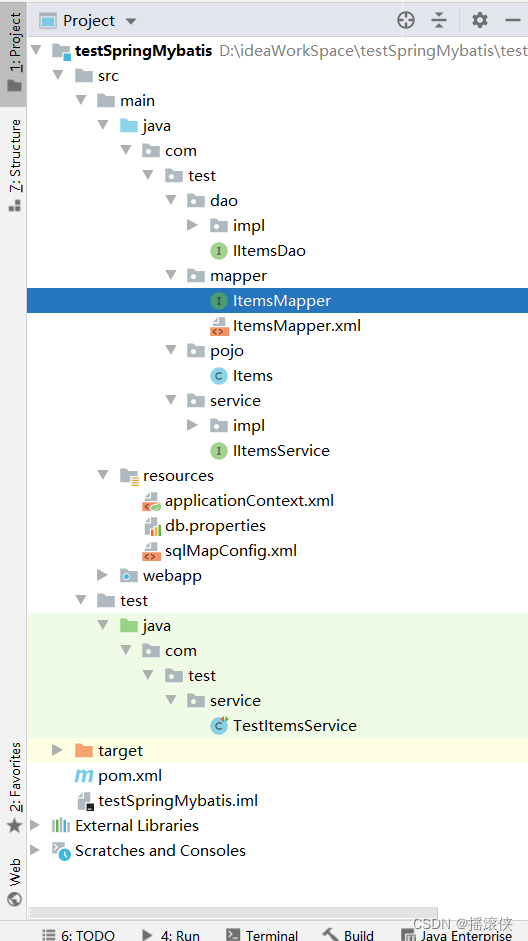
javaee spring整合mybatis spring帮我们创建dao层
项目结构 pom依赖 <?xml version"1.0" encoding"UTF-8"?><project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/P…...
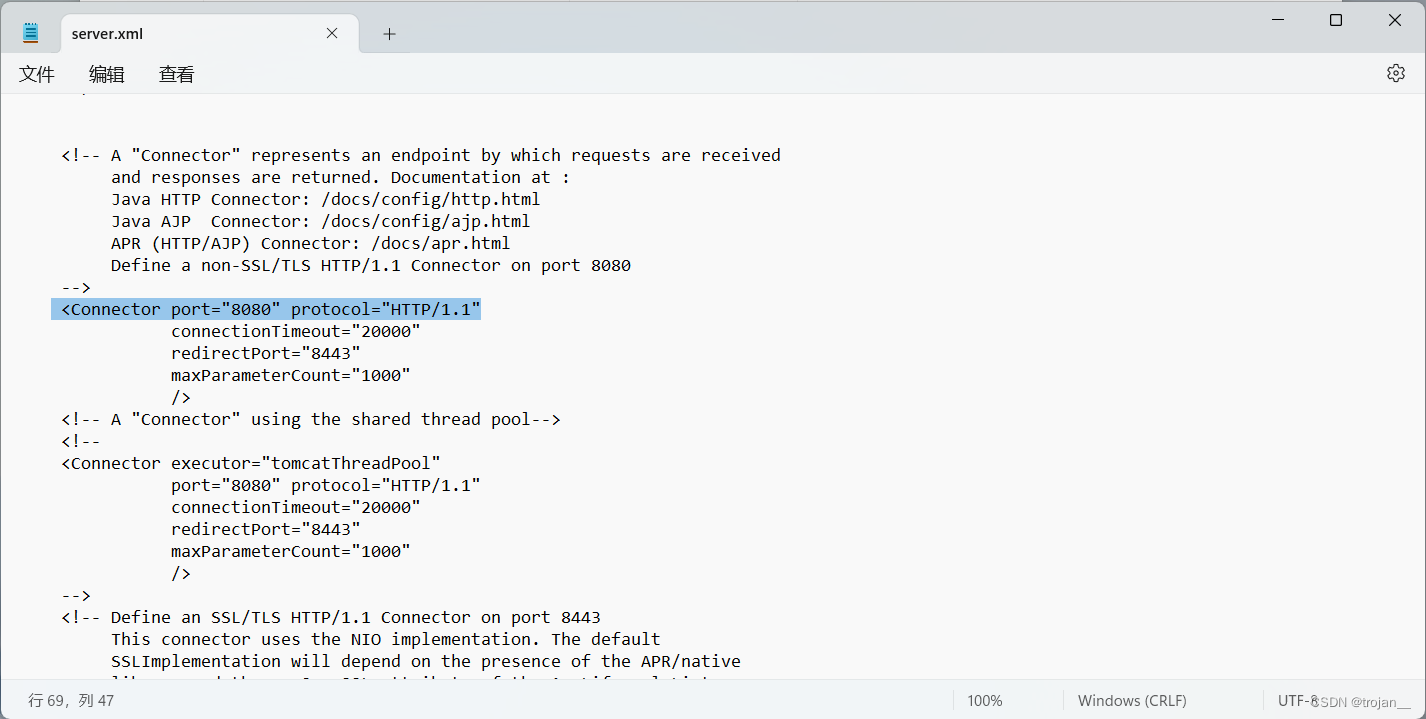
修改Tomcat的默认端口号
1、找到Tomcat的安装路径。 2、打开conf文件夹。 3、用记事本打开server.xml文件 4、找到 <Connector port"8080" protocol"HTTP/1.1",其中的8080就是tomcat的默认端口,将其修改为你需要的端口即可。...

Open3D Ransac拟合空间直线(python详细过程版)
RANSAC拟合直线 一、算法原理1、算法简介2、参考文献二、代码实现三、结果展示本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫。 一、算法原理 1、算法简介 见:Open3D——RANSAC 三维点云空间直线拟合 2、参考文献...

题目:2729.判断一个数是否迷人
题目来源: leetcode题目,网址:2729. 判断一个数是否迷人 - 力扣(LeetCode) 解题思路: 对 n,2*n,3*n 中的数字出现次数计数,若数字 0 出现 0 次,数字 1~9…...
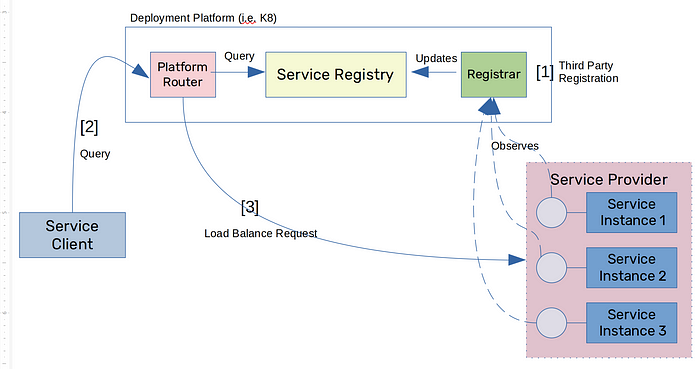
微服务模式:服务发现模式
由于微服务应用的动态性,很难调用具有固定 IP 地址的服务。这就是服务发现的概念出现的背景。服务发现有助于客户端了解服务实例的位置。在这种情况下,服务发现组件将充当服务注册表。 服务注册表是一个包含服务实例位置的集中式服务器/数据库。在微服务…...
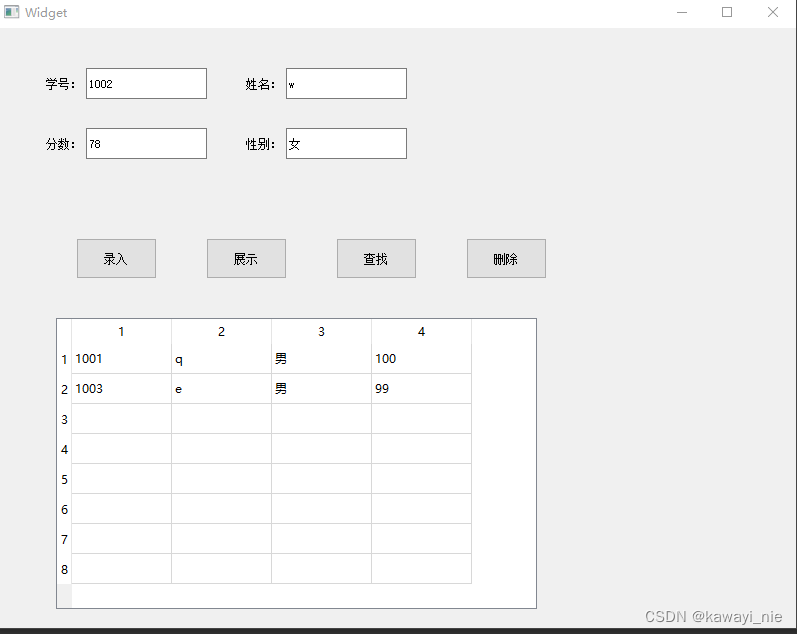
9.4 数据库 TCP
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);//判断数据库对象是否包含了自己使用的数据库if(!db.contains("Stu.db")){//不存在数据库࿰…...
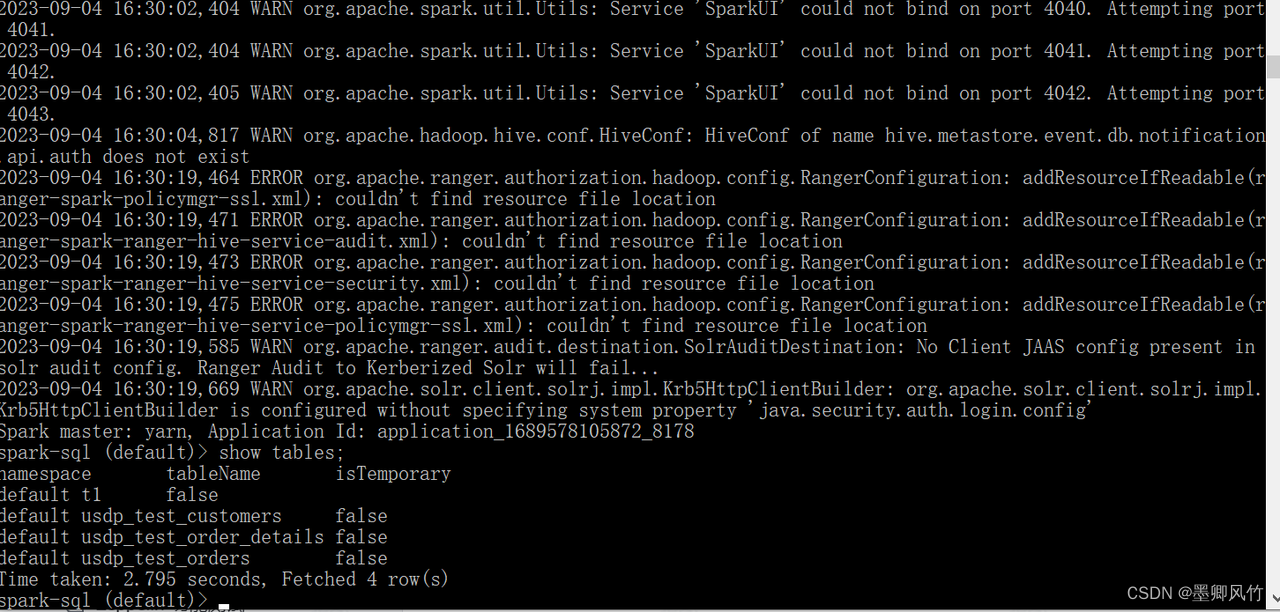
普通用户使用spark的client无法更新Ranger策略
普通用户使用spark的client无法更新Ranger策略 报错图片: WARN org.apache.ranger.admin.client.RangerAdminRESTClient: Error getting Roles. secureModetrue, usercaojianxiangUCDIPA.VIATRIS.CC (auth:KERBEROS),responsef"httpStatusCode&quo…...

Git超详细教程
文章目录 一、安装并配置Git二、Git的基本操作三、Github/GitLab/Gitee四、分支 一、安装并配置Git 查看所有的全局配置项 git config --list --global查看指定的全局配置项 git config user.name git config user.email配置用户信息 git config --global user.name "…...

C++ 回调函数
一、使用方法 1.定义一个函数指针 typedef int (*pCallback)(int a, int b);2.定义一个带参的回调函数(注释部分是普通回调函数,不用定义第一步里的函数指针) //带参 int oneCallback(int a, int b, pCallback p) //int oneCallback(int a, i…...

xilinx FPGA IOB约束使用以及注意事项
文章目录 一、什么是IOB约束二、为什么要使用IOB约束1、在约束文件中加入下面约束:2、直接在代码中加约束, 三、IOB约束使用注意事项 一、什么是IOB约束 在xilinx FPGA中,IOB是位于IO附近的寄存器,是FPGA上距离IO最近的寄存器&am…...
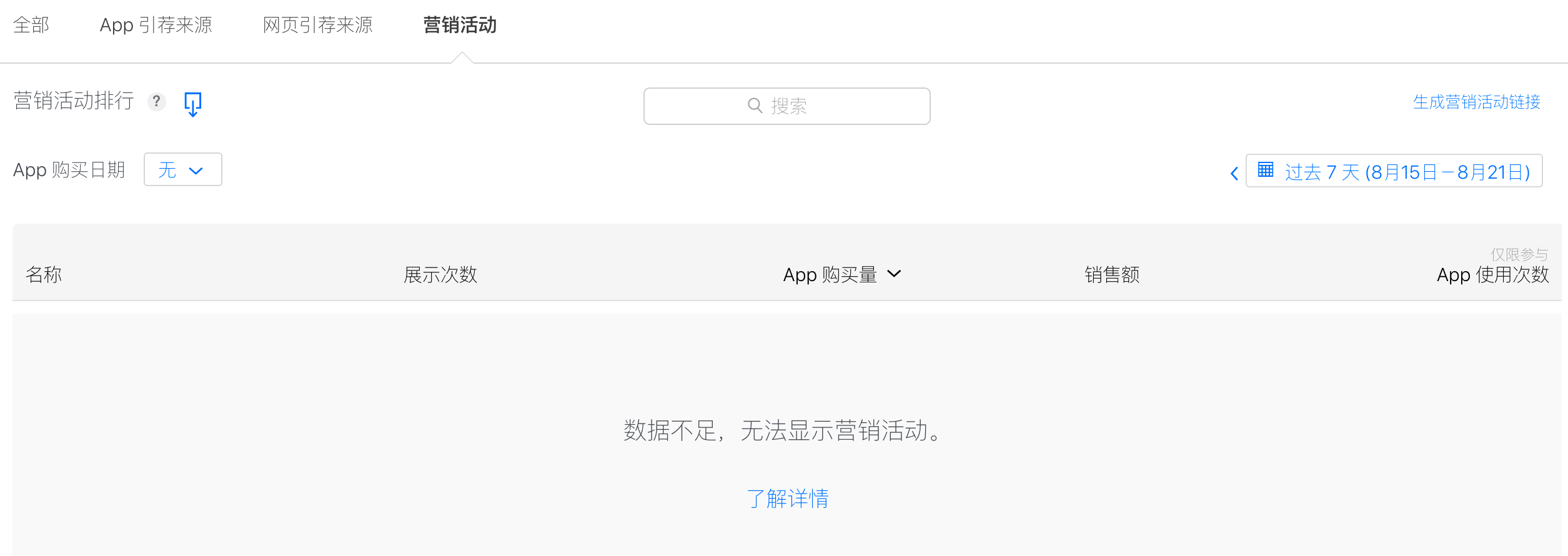
如何统计iOS产品不同渠道的下载量?
一、前言 在开发过程中,Android可能会打出来很多的包,用于标识不同的商店下载量。原来觉得苹果只有一个商店:AppStore,如何做出不同来源的统计呢?本篇文章就是告诉大家如何做不同渠道来源统计。 二、正文 先看一下苹…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
