二叉树的顺序结构以及堆的实现——【数据结构】

W...Y的主页 😊
代码仓库分享 💕
上篇文章,我们认识了什么是树以及二叉树的基本内容、表示方法……接下来我们继续来深入二叉树,感受其中的魅力。
目录
二叉树的顺序结构
堆的概念及结构
堆的实现
堆的创建
堆的初始化与释放空间
堆的插入
堆的删除
堆实现的代码接口,以及简单函数的直接实现
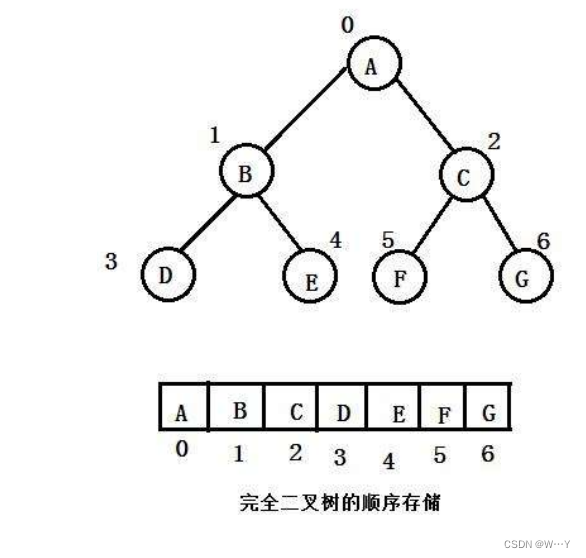
二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。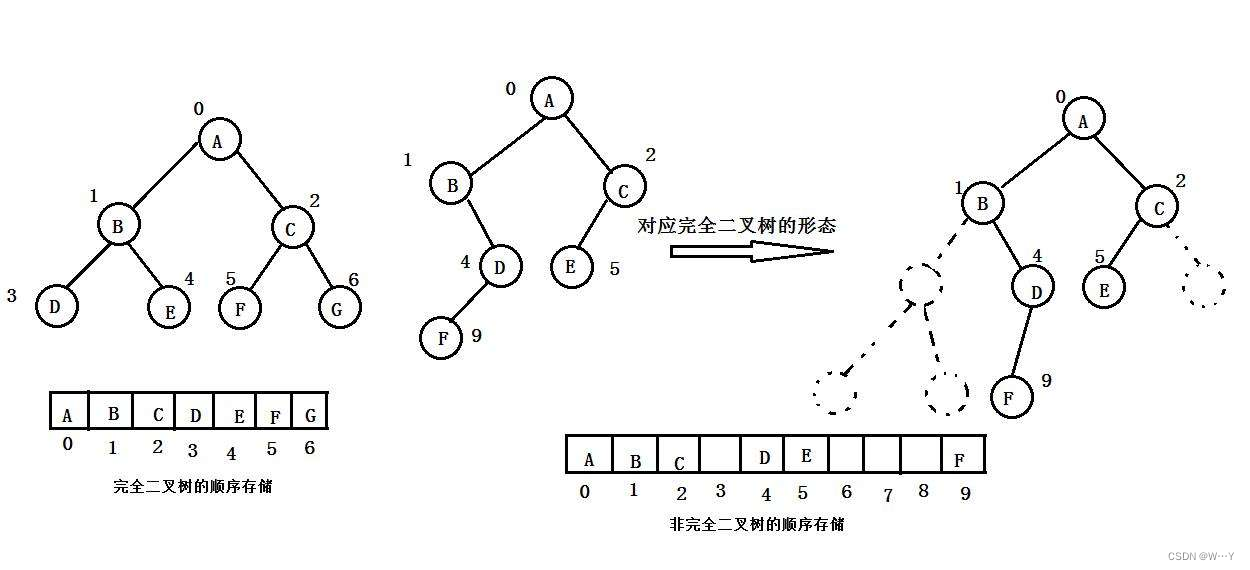
顺序存储又叫数组存储,是指一层一层存入数组中去。物理层面上是一个数组,在逻辑上面是一个二叉树!!!
而在顺序存储中有一些规律:
通过父节点可以找到自己左右两个孩子:
左孩子:leftchild = parent*2+1;
右孩子:rightchild = parent*2+2;
通过孩子节点可以找到父节点:
parent = (child-1)/2;
因为我们将数据按照二叉树的规律存入数组中(从上到下、从左往右)所以父节点与子节点就有一些特殊的规律,这个是我们经常会用到的,需要我们熟记于心!!!
总结:如果强行将一个普通的二叉树用数组存储,会浪费许多空间。所以只有满二叉树与完全二叉树才可以进行数组顺序存储。
堆的概念及结构
这个堆与操作系统中的堆不同,操作系统将内存存储划分为栈区、堆区、静态区……而这个堆是一种数据结构。
堆的概念:
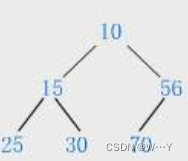
如果有一个关键码的集合K = {k0 ,k1 ,k2 ,…,kn-1 },把它的所有元素按完全二叉树的顺序存储方式存储
在一个一维数组中,并满足: ki<=k(2*i+1) 且ki <=k(2*i+2) ( ki>=k(2*i+1) 且 ki>=k(2*i+2)) i = 0,1,2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。(以上k后面的数字以及表达式全部为角标i)
堆的性质:
堆中某个节点的值总是不大于或不小于其父节点的值;
堆总是一棵完全二叉树。
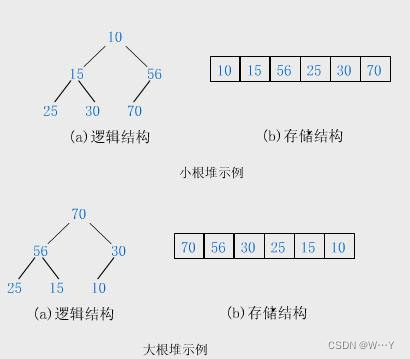
小堆:树中任何一个父亲的值都<=孩子的值
大堆:树中任何一个父亲的值都>=孩子的值
小堆那堆的底层数组是否为升序呢?
不一定!
这个堆转换成数组为:10 15 56 25 30 70明显不是升序,堆只能保证父亲小于(大于)孩子,并不是与堂兄第比较。但是我们可以发现小堆的根是整棵树中最小值。
所以我们可以利用发现解决topk问题与堆排序。
堆排序是非常快的,时间复杂度只有O(N*logN)
堆的实现
堆的创建
想要实现堆,我们先来表示堆,堆的创建其实就与顺序表大同小异,因为在物理层面上就是一个数组。
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;创建指针指向将要动态开辟的数组中,size记录有效存储数据个数,capacity记录开辟空间大小。
堆的初始化与释放空间
还是与顺序表相同,我们将堆中指针置空,size与capacity赋值0即可。
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = 0;php->capacity = 0;
}释放空间也非常简单,free掉开辟的空间,指针置空,size与capacity赋值0即可。
void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}堆的插入
堆的实现原理是数组,所以我们使用尾插非常方便。但是堆的要求是父亲节点必须大于或小于孩子节点,所以我们在插入时有很多情况。就以小堆为例:

这里最坏的情况就是插入一个数,最后与根交换才能成为小堆。这里我们可以创建一个向上调整函数,当插入一个数据时,我们得进行比较调换让其继续保存小堆!!!
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}我们传入这个数组,再将新插入的数据下标给予向上调整函数,利用二叉树在数组中存储的规律找到父节点进行比较,如果子节点小于父节点则break退出循环,反之子节点大于父节点进行交换继续寻找交换后的父节点进行比较,直到满足小堆或child>0结束循环。
Swap交换函数:
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}而创建插入函数就与顺序表极为相似,先判断空间是否足够,然后将新的数据插入数组中,最后调用向上调整判断是否满足小堆条件。
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->capacity == php->size){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("realloc");exit(-1);}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}堆的删除
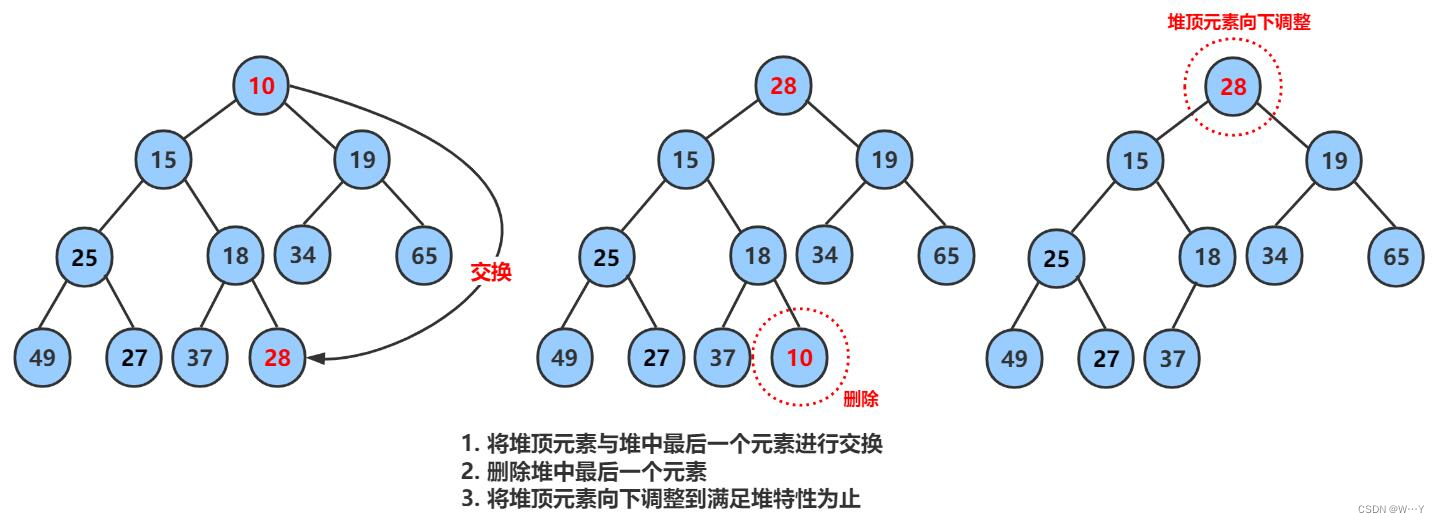
堆的删除中,我们删除数组的尾元素就没有意义,所以一般删除堆是删除堆顶元素。那怎么删除才能保证满足小堆条件呢?
我们不能直接将堆顶元素删除,然后将数组中的其他元素往前挪一位,这样有极大的可能不满足堆的条件。如果按照上述方法继续进行,然后从新使用向上调整进行排序这样时间复杂度会很高,那有什么方法可以优化呢?
我们可以将堆顶的数据根最后一个数据一换,然后删除数组最后一个数据,再进行向下调
整算法。
将堆顶的元素交换到下面去先进行尾删覆盖,再进行向下调整就可以完成堆顶的删除。
那如何创建向下调整函数呢?
我们先创建将数组指针进行接收,然后传入数组的大小以及已经交换过需要调整元素的下标0
然后通过二叉树在数组中存储的规律找到左孩子节点,让左孩子与右孩子进行比较,谁小谁才有机会与父节点进行比较交换。以此类推即可满足小堆要求。
void AdjustDown(HPDataType* a, int n, int parent) {int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}} }特别注意:我们在找到左孩子节点之后,要让左孩子与右孩子进行比较时,我们必须要加入限制条件child+1<n,否则会造成数组越界访问的后果!!!
而删除堆函数就非常简单了,只需要将头与尾进行交换后调用向下调整函数即可。
void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);--php->size;AdjustDown(php->a, php->size, 0);
}堆实现的代码接口,以及简单函数的直接实现
typedef int HPDataType;
typedef struct Heap
{
HPDataType* _a;
int _size;
int _capacity;
}Heap;
// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{assert(php);assert(php->size > 0);return php->a[0];
}
// 堆的判空
int HeapEmpty(Heap* hp);
{assert(hp);return hp->size == 0;
}以上就是二叉树的顺序结构以及堆排序实现的全部内容,下一篇文章我们就要学习关于堆最经典的堆排序以及topk问题,敬请期待。
感谢大家观看,一键三连是对博主最大的鼓励,博主因为你们的阅读而开心,希望博主的分享可以帮助许多人❤️❤️❤️
相关文章:
二叉树的顺序结构以及堆的实现——【数据结构】
W...Y的主页 😊 代码仓库分享 💕 上篇文章,我们认识了什么是树以及二叉树的基本内容、表示方法……接下来我们继续来深入二叉树,感受其中的魅力。 目录 二叉树的顺序结构 堆的概念及结构 堆的实现 堆的创建 堆的初始化与…...

手写一个摸鱼神器:使用python手写一个看小说的脚本,在ide中输出小说内容,同事直呼“还得是你”
文章目录 一、准备python环境二、分析小说网的章节目录三、分析小说网的章节内容四、编写python脚本五、验证一下吧 一、准备python环境 windows从0搭建python3开发环境与开发工具 Python爬虫基础(一):urllib库的使用详解 Python爬虫基础&a…...
【Python 实战】---- 实现批量图片的切割
1. 需求场景 在实际开发中,我们会遇到一种很无聊,但是又必须实现的需求,就是比如协议、大量的宣传页面、大量的静态介绍页面、或者大量静态页面,但是页面高度很高,甚至高度可能会达到50000px,但是为了渲染…...
MAYA粒子基础_场
重力场 牛顿场 径向场 均匀场和重力场的区别 空气场 推动物体 阻力场 推动物体 涡流场 湍流场 体积轴场...

趣解设计模式之《我买了宝马,为啥不让我停这?》
〇、小故事 我们怎么识别一辆汽车是宝马品牌的汽车呢?虽然宝马汽车车辆型号非常的多,而且外型也各不相同,但是只要是宝马品牌的汽车,它的车头一定会有宝马汽车的logo,那么这个就是大家最直观去确认一辆车是不是宝马牌…...

MyBatis Plus 中 LocalDateTime 引发的一些问题和解决办法
简介 在使用 MyBatis Plus 进行数据库操作时,我们经常会遇到处理日期时间类型的需求。然而,在某些情况下,使用 LocalDateTime 类型可能会引发一些问题。本文将详细介绍这些问题,并提供相应的解决办法。 问题描述: 1…...
谁懂啊!自制的科普安全手册居然火了
自制的科普安全手册居然火了 谁懂啊! 嗨嗨嗨!小仙女们,有没有见过这样的可以翻页的电子安全手册呢?自己随手就能轻松制作手册,结果一晚浏览量这么多!这可真是让人又惊又喜啊!快来分享一下我的喜…...
强化学习-论文调研-泛化性能力度量
1.[ICML2019]Quantifying Generalization in Reinforcement Learning 文章提出16000多个单智能体闯关游戏CoinRun,通过智能体在分割开的训练环境和测试环境上表现的性能作为RL泛化性的度量。具体而言作者通过”奔跑硬币泛化曲线“ (CoinRun Gener…...

CSS中图片旋转超出父元素解决办法
下面的两种解决办法都会导致图片缩小,可以给图片进行初始化的宽高设置 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge">…...

QML、C++ 和 JS 三者之间的交互
QML、C++ 和 JS 三者之间的交互是 Qt Quick 应用开发的核心。以下是它们之间交互的常见方式: 从 QML 调用 C++ 函数要从 QML 调用 C++ 函数,您可以使用 Qt 的 QML 注册机制,例如 qmlRegisterType,将 C++ 类注册为 QML 类型。 C++ 代码: #include <QGuiApplication>…...
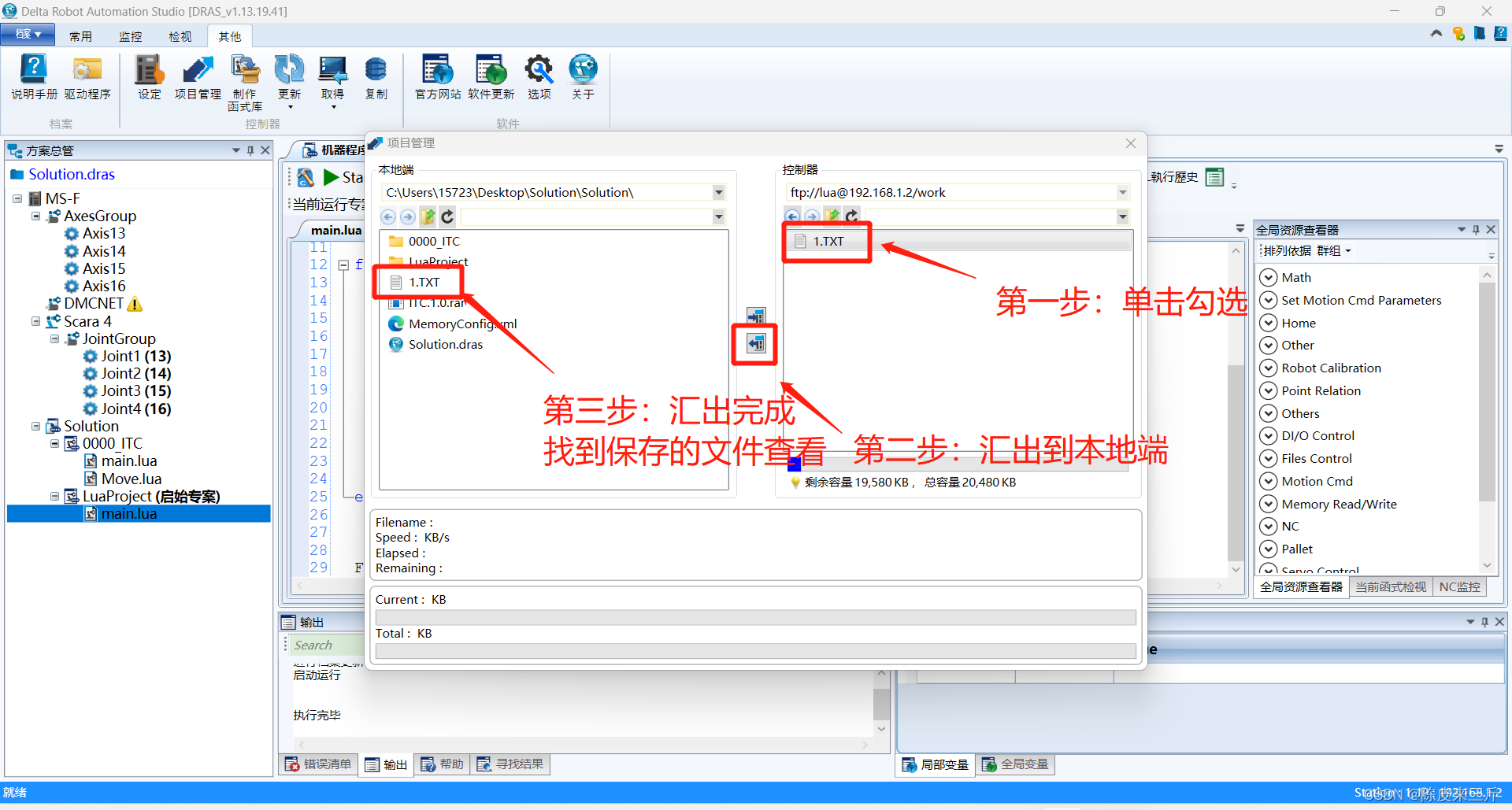
ProEasy机器人:TCP无协议通讯(socket通讯)时打印log日志
打印日志需要调用lua中的io相关文件函数与os相关时间函数,代码如下 --------TCP无协议视觉通讯------- function open_client_Vision() --连接视觉服务器 打开以太网作为客户端 repeat FreePort.ECM_CloseAll() --关闭所有链接 …...
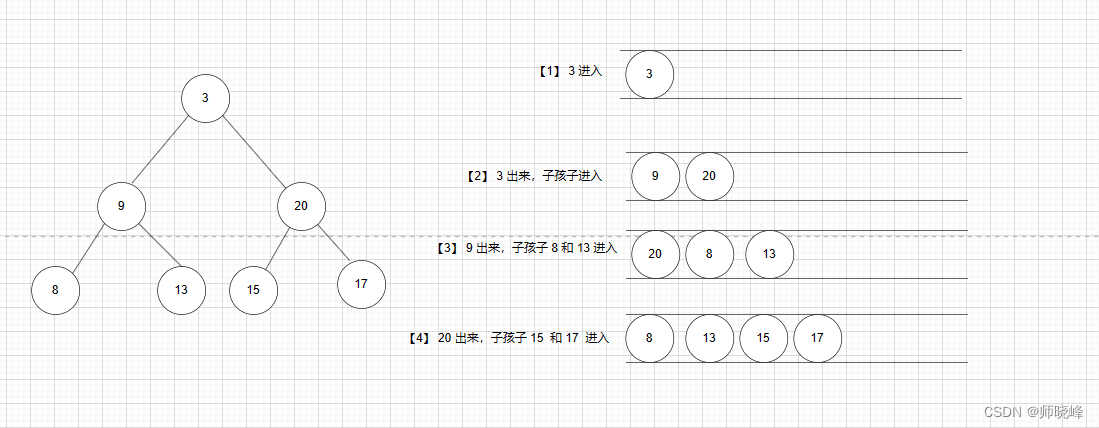
算法通过村第六关-树白银笔记|层次遍历
文章目录 前言1. 层次遍历介绍2. 基本的层次遍历与变换2.1 二叉树的层次遍历2.2 层次遍历-自底向上2.3 二叉树的锯齿形层次遍历2.4 N叉树的层次遍历 3. 几个处理每层元素的题目3.1 在每棵树行中找出最大值3.2 在每棵树行中找出平均值3.3 二叉树的右视图3.4 最底层最左边 总结 前…...

SpringCloud理解篇
一、微服务概述 1、什么是微服务 目前的微服务并没有一个统一的标准,一般是以业务来划分将传统的一站式应用,拆分成一个个的服务,彻底去耦合,一个微服务就是单功能业务,只做一件事。 与微服务相对的叫巨石 。 2、微服…...

编写LED灯的驱动,实现三盏灯的控制
mychrdev.c #include <linux/init.h> #include <linux/module.h> #include <linux/fs.h> #include <linux/uaccess.h> #include <linux/io.h> #include "head.h"unsigned int major; // 保存主设备号 char kbuf[128]{0}; unsigned int…...

Flink报错处理-1
在 flink job 运行一段时间后,观察日志发现出现了如下的 warn日志: The operator name {} exceeded the {} characters length limit and was truncated 完整的 warn 日志如下: The operator name TriggerWindow(GlobalWindows(), ListStat…...

bim与数字孪生智能建造的关系
随着建筑业数字化改革的推进,我们正迈入数字孪生时代,而真正实现建筑物数字孪生的智能建造,其基础前提是建造对象和建造过程的高度数字化,这样一个过程唯有依托BIM建立数据模型才能实现,真正达到智能建造或智慧运维。 …...
:守护进程)
【Linux】进程篇(补):守护进程
文章目录 1. 补充1.1 查看1.2 控制进程组的方式 2. 创建守护进程step1. 忽略信号step2. 让自己不是组长step3. setsid 函数:给调用函数设置新的会话和进程组 IDstep4. chdir 函数:可以改变守护进程的工作路径step5. 处理文件描述符 0、1、2 守护进程类样…...

SpringMVC自定义视图完成步骤 和 视图解析的源码剖析
自定义视图完成步骤: ● 7.2.1自定义视图完成步骤 1. 自定义视图**:** 创建一个 View 的 bean, 该 bean 需要继承自 AbstractView, 并实现 renderMergedOutputModel 方法**.** 2. 并把自定义 View 加入到 IOC 容器中 3. 自定义视图的视图处理器,使用…...

合宙Air724UG LuatOS-Air lvgl字库
目录 LVGL 简介1. lvgl自带字库 特点使用场景2. lvgl加载外部字体 软件接口使用场景3. lvgl 矢量字体 软件接口硬件外接SPI字库芯片详细使用示例使用场景常见问题 LVGL 简介 LVGL字库有3种方式可以使用,刚接触的客户可能不太了解怎样选用,以下对这3种…...

C#,数值计算——指数微分(exponential deviates)的计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { /// <summary> /// 指数偏差 /// Structure for exponential deviates. /// </summary> public class Expondev : Ran { private double beta { get; set; } /// <s…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...