文心一言 VS 讯飞星火 VS chatgpt (91)-- 算法导论8.3 4题
四、用go语言,说明如何在 O(n) 时间内,对 0 到 n 3 − 1 n^3-1 n3−1 区间内的n个整数进行排序。
文心一言:
在 O(n) 时间内对 0 到 n^3-1 区间内的 n 个整数进行排序,可以使用基数排序(Radix Sort)算法。基数排序是一种非比较型整数排序算法,其时间复杂度为 O(d*(n+k)),其中 d 是数字的最大位数,k 是基数(通常为 10)。
下面是使用 Go 语言实现基数排序的示例代码:
package main import ( "fmt" "math/rand"
) func radixSort(arr []int) { // 获取数组中最大的数 max := arr[0] for _, num := range arr { if num > max { max = num } } // 计算最大数的位数 maxDigit := 1 for max/10 > 0 { max /= 10 maxDigit++ } // 对每一位进行计数排序 for digit := 1; digit <= maxDigit; digit++ { // 计数数组,用于存储当前位上每个数字出现的次数 count := make([]int, 10) // 统计当前位上每个数字出现的次数 for _, num := range arr { count[num/(10^(digit-1))%10]++ } // 累计计数数组,用于确定每个数字在结果数组中的位置 for i := 1; i < 10; i++ { count[i] += count[i-1] } // 从右往左遍历原数组,将数字按照当前位上的值放入结果数组中 result := make([]int, len(arr)) for i := len(arr) - 1; i >= 0; i-- { index := count[arr[i]/(10^(digit-1))%10] - 1 result[index] = arr[i] count[arr[i]/(10^(digit-1))%10]-- } // 将结果数组复制回原数组 copy(arr, result) }
} func main() { n := 10 // 数组大小 arr := make([]int, n) for i := 0; i < n; i++ { arr[i] = rand.Intn(n*n*n) // 生成随机整数 } fmt.Println("排序前:", arr) radixSort(arr) fmt.Println("排序后:", arr)
}
在这个示例中,我们首先生成一个包含 n 个随机整数的数组。然后,我们使用基数排序算法对数组进行排序。首先,我们找到数组中的最大数,并计算其位数。接下来,我们从最低位开始,对每一位进行计数排序。我们使用计数数组来统计当前位上每个数字出现的次数,然后累计计数数组以确定每个数字在结果数组中的位置。最后,我们将数字按照当前位上的值放入结果数组中。通过循环遍历数字的每一位,我们最终得到排序后的数组。

讯飞星火:
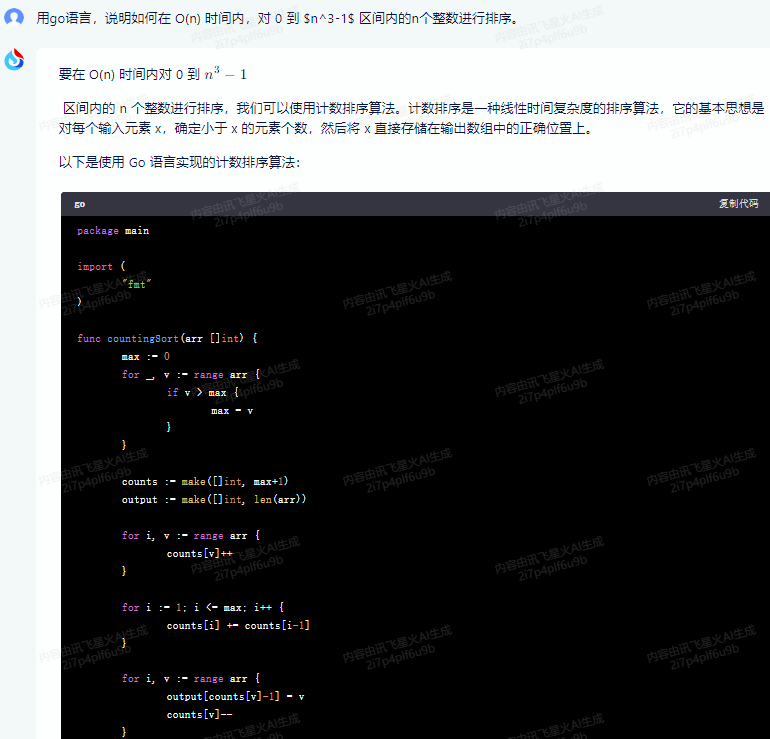
要在 O(n) 时间内对 0 到 n 3 − 1 n^3-1 n3−1 区间内的 n 个整数进行排序,我们可以使用计数排序算法。计数排序是一种线性时间复杂度的排序算法,它的基本思想是对每个输入元素 x,确定小于 x 的元素个数,然后将 x 直接存储在输出数组中的正确位置上。
以下是使用 Go 语言实现的计数排序算法:
package mainimport ("fmt"
)func countingSort(arr []int) {max := 0for _, v := range arr {if v > max {max = v}}counts := make([]int, max+1)output := make([]int, len(arr))for i, v := range arr {counts[v]++}for i := 1; i <= max; i++ {counts[i] += counts[i-1]}for i, v := range arr {output[counts[v]-1] = vcounts[v]--}copy(arr, output)
}func main() {arr := []int{4, 2, 2, 8, 3, 3, 1}fmt.Println("Before sorting:", arr)countingSort(arr)fmt.Println("After sorting:", arr)
}
这段代码首先找到数组中的最大值,然后创建一个计数数组和一个输出数组。接下来,我们遍历输入数组,统计每个元素的出现次数。然后,我们更新计数数组,使其表示每个元素在输出数组中的结束位置。最后,我们将输入数组中的元素复制到输出数组的正确位置上。

360智脑:
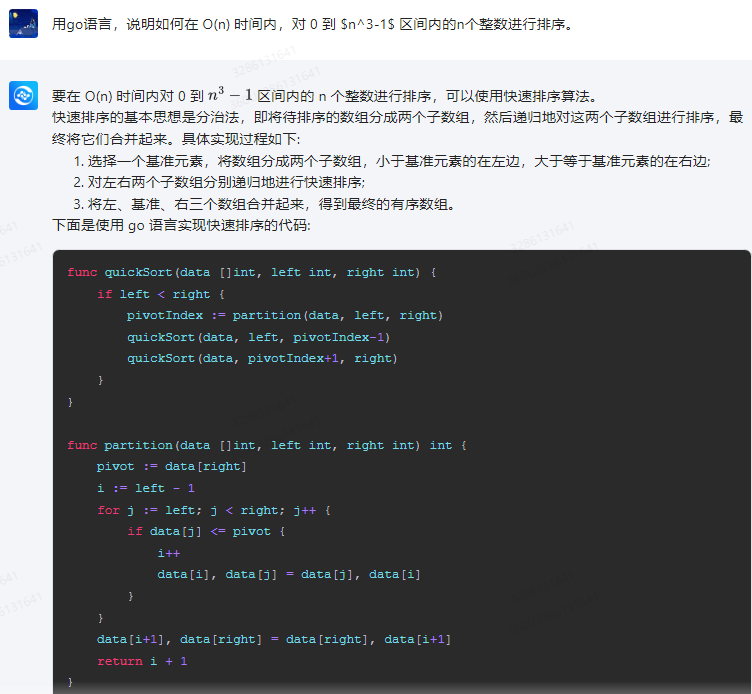
要在 O(n) 时间内对 0 到 n 3 − 1 n^3-1 n3−1 区间内的 n 个整数进行排序,可以使用快速排序算法。
快速排序的基本思想是分治法,即将待排序的数组分成两个子数组,然后递归地对这两个子数组进行排序,最终将它们合并起来。具体实现过程如下:
1.选择一个基准元素,将数组分成两个子数组,小于基准元素的在左边,大于等于基准元素的在右边;
2.对左右两个子数组分别递归地进行快速排序;
3.将左、基准、右三个数组合并起来,得到最终的有序数组。
下面是使用 go 语言实现快速排序的代码:
func quickSort(data []int, left int, right int) {if left < right {pivotIndex := partition(data, left, right)quickSort(data, left, pivotIndex-1)quickSort(data, pivotIndex+1, right)}
}func partition(data []int, left int, right int) int {pivot := data[right]i := left - 1for j := left; j < right; j++ {if data[j] <= pivot {i++data[i], data[j] = data[j], data[i]}}data[i+1], data[right] = data[right], data[i+1]return i + 1
}
其中,quickSort 函数用于递归地对左右两个子数组进行快速排序,partition 函数用于将待排序的数组分成小于基准元素和大于等于基准元素的两个子数组。
时间复杂度分析:每次递归都将待排序的数组分成两个子数组,最多需要进行 n 2 \frac{n}{2} 2n 次递归,因此时间复杂度为 O( n log n n\log n nlogn)。但是,在最好的情况下,即待排序的数组已经有序的情况下,快速排序的时间复杂度可以达到 O( n n n)。因此,在实际应用中,快速排序通常是最快的排序算法之一。

智谱清言:
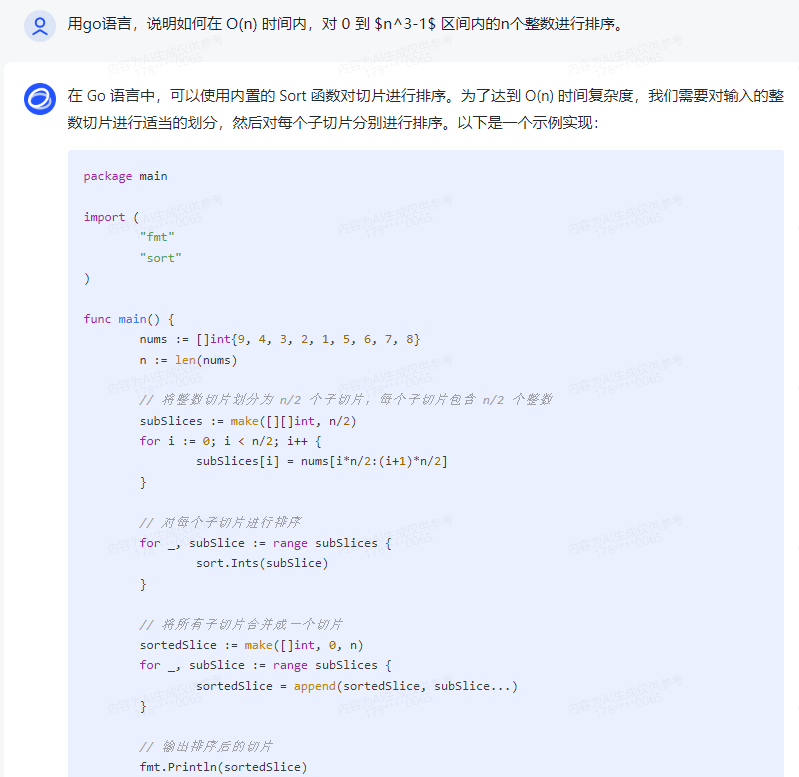
在 Go 语言中,可以使用内置的 Sort 函数对切片进行排序。为了达到 O(n) 时间复杂度,我们需要对输入的整数切片进行适当的划分,然后对每个子切片分别进行排序。以下是一个示例实现:
package main
import ( "fmt" "sort"
)
func main() { nums := []int{9, 4, 3, 2, 1, 5, 6, 7, 8} n := len(nums)// 将整数切片划分为 n/2 个子切片,每个子切片包含 n/2 个整数 subSlices := make([][]int, n/2) for i := 0; i < n/2; i++ { subSlices[i] = nums[i*n/2:(i+1)*n/2] }// 对每个子切片进行排序 for _, subSlice := range subSlices { sort.Ints(subSlice) }// 将所有子切片合并成一个切片 sortedSlice := make([]int, 0, n) for _, subSlice := range subSlices { sortedSlice = append(sortedSlice, subSlice...) }// 输出排序后的切片 fmt.Println(sortedSlice)
}
这个示例首先将输入的整数切片划分为 n/2 个子切片,每个子切片包含 n/2 个整数。然后对每个子切片分别进行排序。最后,将所有子切片合并成一个切片并输出。
需要注意的是,这个实现假设输入的整数切片中的元素是已知的,并且需要在 O(n) 时间内进行排序。如果需要在运行时动态生成整数切片并进行排序,那么可能需要考虑使用其他数据结构和算法来优化时间复杂度。

通义千问:
可以使用归并排序的思想,在 O(n) 时间内对 0 到 n 3 − 1 n^3-1 n3−1 区间内的n个整数进行排序。
具体实现方法如下:
1.将 0 到 n 3 − 1 n^3-1 n3−1 区间内的n个整数划分为n个子区间,每个子区间的长度为 n 2 n^2 n2。
2.对每个子区间进行快速排序,时间复杂度为 O(n)。
3.将排好序的子区间依次合并,时间复杂度为 O(n)。
下面是具体的代码实现:

天工:
可以使用基数排序(Radix Sort)算法,在O(n)时间内对0到
�
3
−
1
n
3
−1区间内的n个整数进行排序。
基数排序是一种非比较排序算法,它根据元素的每个位数来排序,具体来说,就是将待排序的n个整数按照二进制位从低到高依次进行排序。
具体实现过程如下:
1.找到待排序数组中的最大值和最小值,计算出它们的位数,记为maxDigit和minDigit,分别表示最大值和最小值在二进制下的位数。
2.将待排序数组中的每个数转换为二进制字符串,然后从最低位开始,依次对每一位进行排序。具体实现过程可以使用桶排序(Bucket Sort)算法,将每个二进制字符串按照当前位数所在的桶进行分类,然后依次对每个桶中的数进行排序。
3.重复步骤2,直到对整个数组进行排序。
下面是使用Go语言实现基数排序的示例代码:
func radixSort(arr []int) {// Step 1: Find the maximum and minimum values and their digit countmaxVal := arr[0]minVal := arr[0]maxDigit := 0minDigit := 0for _, val := range arr {if val > maxVal {maxVal = val}if val < minVal {minVal = val}digitCount := 0for val != 0 {digitCount++val /= 10}if digitCount > maxDigit {maxDigit = digitCount}if digitCount < minDigit {minDigit = digitCount}}// Step 2: Convert each number to a binary string and sort each digitbuckets := make([][]int, maxDigit+1)for _, val := range arr {digit := int(val) % 10buckets[digit] = append(buckets[digit], val)// Move elements from lower digits to higher digitsfor i := digit - 1; i >= 0; i-- {if len(buckets[i]) > 0 {for _, val := range buckets[i] {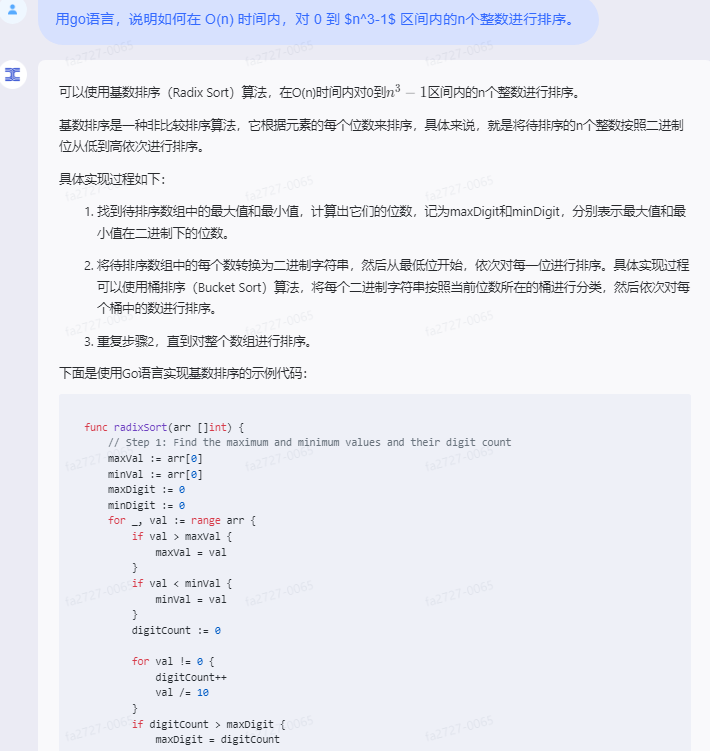

chatgpt:
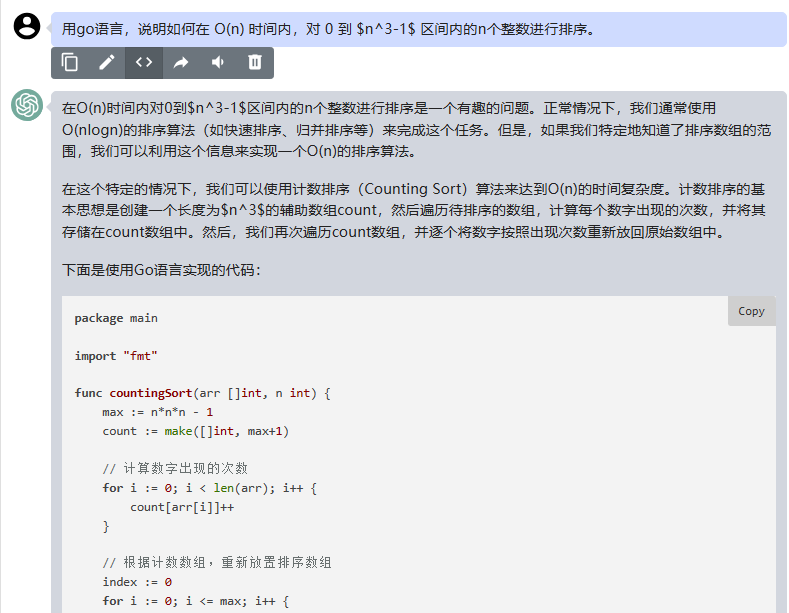
在O(n)时间内对0到 n 3 − 1 n^3-1 n3−1区间内的n个整数进行排序是一个有趣的问题。正常情况下,我们通常使用O(nlogn)的排序算法(如快速排序、归并排序等)来完成这个任务。但是,如果我们特定地知道了排序数组的范围,我们可以利用这个信息来实现一个O(n)的排序算法。
在这个特定的情况下,我们可以使用计数排序(Counting Sort)算法来达到O(n)的时间复杂度。计数排序的基本思想是创建一个长度为 n 3 n^3 n3的辅助数组count,然后遍历待排序的数组,计算每个数字出现的次数,并将其存储在count数组中。然后,我们再次遍历count数组,并逐个将数字按照出现次数重新放回原始数组中。
下面是使用Go语言实现的代码:
package mainimport "fmt"func countingSort(arr []int, n int) {max := n*n*n - 1count := make([]int, max+1)// 计算数字出现的次数for i := 0; i < len(arr); i++ {count[arr[i]]++}// 根据计数数组,重新放置排序数组index := 0for i := 0; i <= max; i++ {for count[i] > 0 {arr[index] = iindex++count[i]--}}
}func main() {n := 10 // 数组大小arr := []int{100, 222, 5, 77, 444, 333, 111, 999, 888, 666}countingSort(arr, n)fmt.Println("排序后的数组:", arr)
}
这段代码首先创建了一个辅助数组count,大小为 n 3 n^3 n3,然后遍历待排序的数组,计算每个数字出现的次数,并将其存储在count数组中。接下来,我们再次遍历count数组,并按照数字出现的次数,逐个将数字重新放回原始数组中。最后,打印排序后的数组。
这个算法的时间复杂度是O(n),因为我们需要遍历待排序的数组两次。但需要注意的是,计数排序的空间复杂度为O(n^3),所以如果n很大,可能会占用过多的内存。

相关文章:

文心一言 VS 讯飞星火 VS chatgpt (91)-- 算法导论8.3 4题
四、用go语言,说明如何在 O(n) 时间内,对 0 到 n 3 − 1 n^3-1 n3−1 区间内的n个整数进行排序。 文心一言: 在 O(n) 时间内对 0 到 n^3-1 区间内的 n 个整数进行排序,可以使用基数排序(Radix Sort)算法…...
keep-alive缓存三级及三级以上路由
需求需要缓存这个出入记录,当tab切换时不重新加载,当刷新页面时,或把这个关闭在重新打开时重新加载如图: (我这里用的是芋道源码的前端框架) keep-alive 1、include 包含页面组件name的这些组件页面,会被…...
vite vue项目 运行时 \esbuild\esbuild.exe 缺失 错误码 errno: -4058, code: ‘ENOENT‘,
vite vue项目运行 npm run dev 报错某个模块启动文件丢失信息 D:\PengYe_code\2\vite-vue3-admin>npm run dev> vite-vue3-admin1.0.2 dev > vitenode:events:504throw er; // Unhandled error event^Error: spawn D:\PengYe_code\2\vite-vue3-admin\node_modules\vi…...
favicon.ico网站图标不显示问题 Failed to load resource: net::ERR_FILE_NOT_FOU
上述问题主要由于网站的小图标无法显示导致的:可以检查如下部分: 1、是否存在一个favicon.ico文件在根目录下 2、如果存在,看是否写的相对路径:改为绝对路径 <link rel"shortcut icon" href"../favicon.ico&quo…...
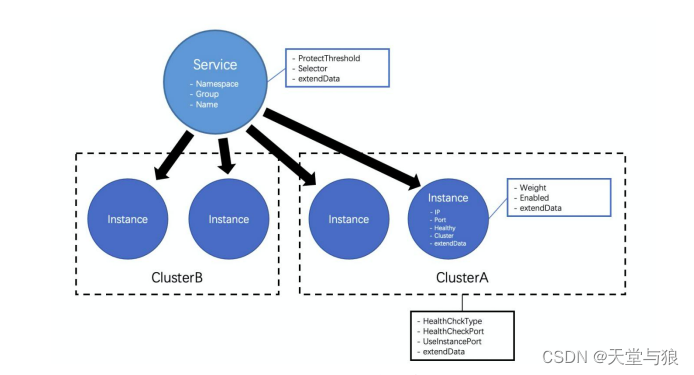
微服务·架构组件之服务注册与发现-Nacos
微服务组件架构之服务注册与发现之Nacos Nacos服务注册与发现流程 服务注册:Nacos 客户端会通过发送REST请求的方式向Nacos Server注册自己的服务,提供自身的元数据,比如ip地址、端口等信息。 Nacos Server接收到注册请求后,就会…...
Linux驱动【day2】
mychrdev.c: #include <linux/init.h> #include <linux/module.h> #include <linux/fs.h> #include<linux/uaccess.h> #include<linux/io.h> #include"head.h" unsigned int major; // 保存主设备号 char kbuf[128]{0}; unsigned int…...
4、Nginx 配置实例-反向代理
文章目录 4、nginx 配置实例-反向代理4.1 反向代理实例一4.1.1 实验代码 4.3 反向代理实例二4.3.1 实验代码 【尚硅谷】尚硅谷Nginx教程由浅入深 志不强者智不达;言不信者行不果。 4、nginx 配置实例-反向代理 4.1 反向代理实例一 实现效果:使用 nginx…...

2023年世界机器人大会回顾
1、前记: 本次记录是我自己去世界机器人博览会参观的一些感受,所有回顾为个人感兴趣部分的机器人产品分享。整个参观下来最大的感受就是科学技术、特别是机器人技术和人工智能毫无疑问地、广泛的应用在我们日常生活的方方面面,在安全巡检、特…...
Mac系统 AndroidStudio Missing essential plugin:org.jetbrains.android报错
打开Android Studio,提示 Missing essential plugin:org.jetbrains.android错误,产生的原因是Kotlin被禁用。 解决的方法是删除disabled_plugins.txt,Mac OS对应的路径为: /Users/xzh/Library/Application Support/Google/AndroidStudio202…...

读书笔记:多Transformer的双向编码器表示法(Bert)-1
多Transformer的双向编码器表示法 Bidirectional Encoder Representations from Transformers,即Bert; 本笔记主要是对谷歌Bert架构的入门学习: 介绍Transformer架构,理解编码器和解码器的工作原理;掌握Bert模型架构…...
第二证券:股利支付率和留存收益率的关系?
股利付出率和留存收益率是股票出资中非常重要的目标,它们可以反映公司的盈余才能和未来开展的潜力。那么,二者之间究竟有什么联系呢? 一、股利付出率和留存收益率的定义 股利付出率是指公司向股东分配的股息占当期净利润的比例,通…...

煤矿虚拟仿真 | 采煤工人VR虚拟现实培训系统
随着科技的发展,虚拟现实(VR)技术已经逐渐渗透到各个行业,其中包括煤矿行业。VR技术可以为煤矿工人提供一个安全、真实的环境,让他们在虚拟环境中进行实际操作和培训,从而提高他们的技能水平和安全意识。 由广州华锐互动开发的采煤…...
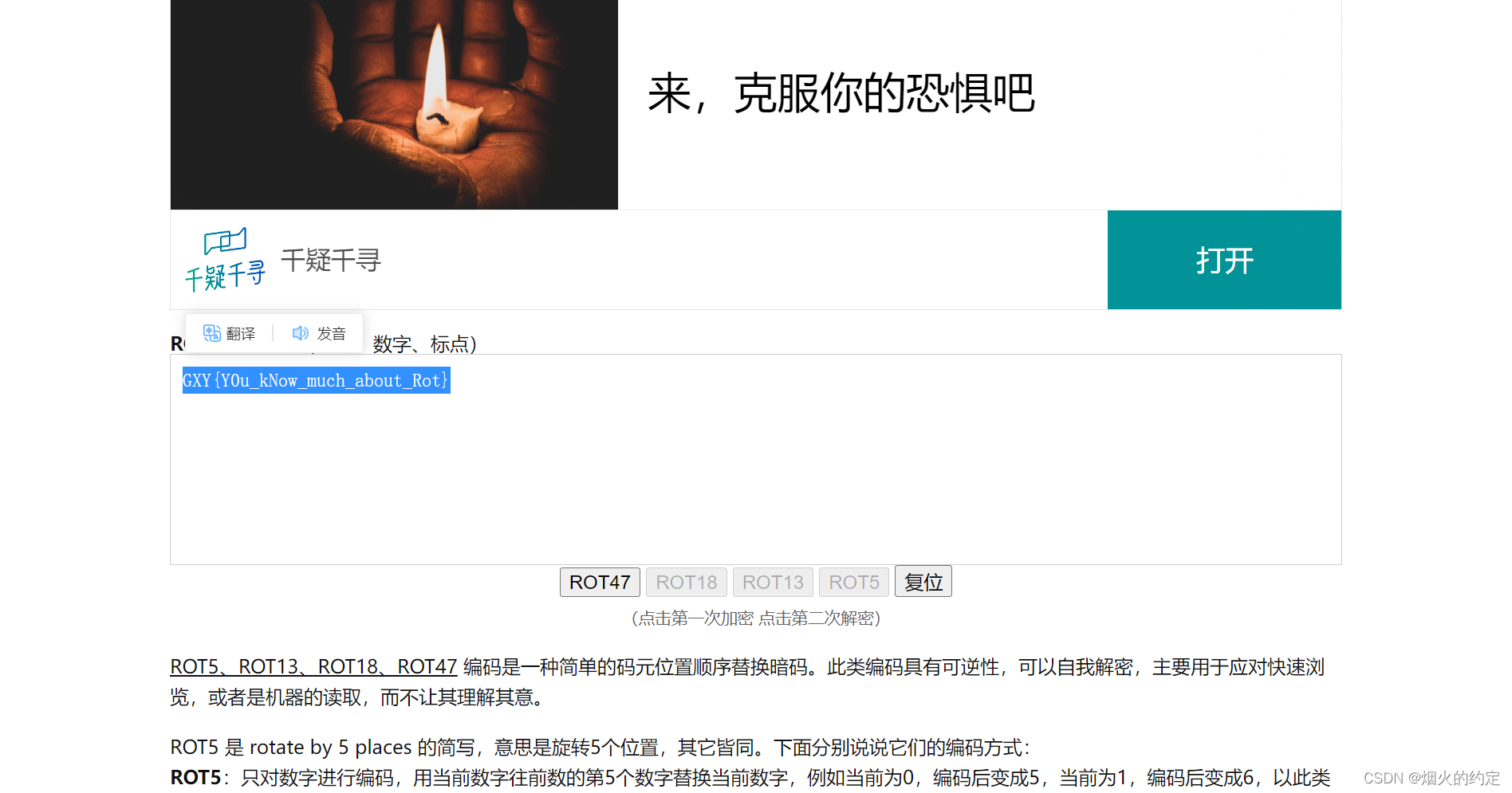
buuctf crypto 【[GXYCTF2019]CheckIn】解题记录
1.打开文件,发现密文 2.一眼base64,解密一下 3.解密后的字符串没有什么规律,看了看大佬的wp,是rot47加密,解密一下(ROT5、ROT13、ROT18、ROT47位移编码)...

微服务05-Docker基本操作
Docker的定义 1.什么是Docker Docker是一个快速交付应用、运行应用的技术: 可以将程序及其依赖、运行环境一起打包为一个镜像,可以迁移到任意Linux操作系统运行时利用沙箱机制形成隔离容器,各个应用互不干扰启动、移除都可以通过一行命令完…...

OpenHarmony创新赛|赋能直播第三期
开放原子开源大赛OpenHarmony创新赛赋能直播间持续邀请众多技术专家一起分享应用开发技术知识,本期推出OpenHarmony应用开发之音视频播放器和三方库的使用和方法,助力开发者掌握多媒体应用技术的开发能力和使用三方库提升应用开发的效率和质量࿰…...
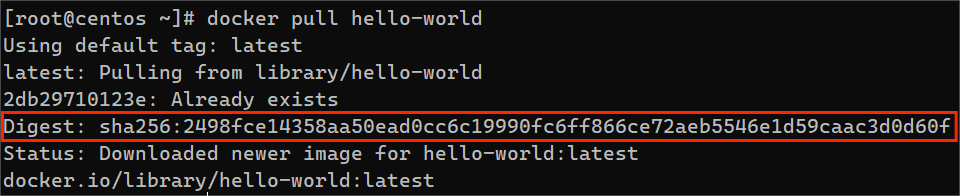
docker镜像详解
目录 什么是docker镜像镜像相关命令docker pulldocker imagesdocker searchdocker rmi导出 / 导入镜像 镜像分层镜像摘要镜像摘要的作用分发散列值 什么是docker镜像 Docker镜像是Docker容器的基础组件,它包含了运行一个应用程序所需的一切,包括代码、运…...
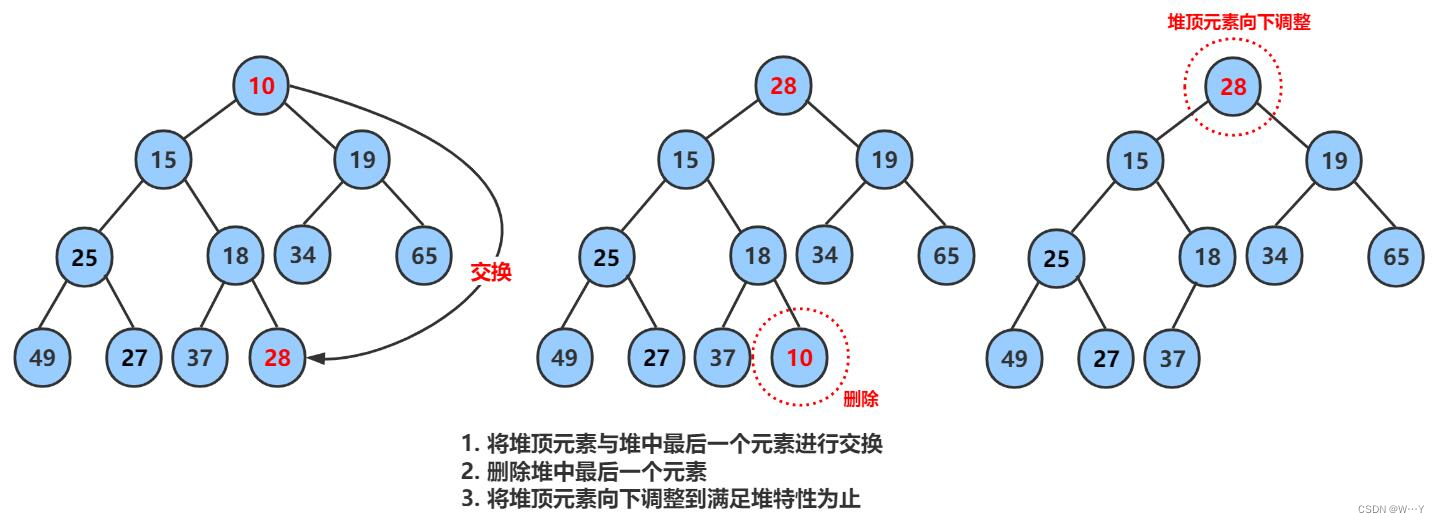
二叉树的顺序结构以及堆的实现——【数据结构】
W...Y的主页 😊 代码仓库分享 💕 上篇文章,我们认识了什么是树以及二叉树的基本内容、表示方法……接下来我们继续来深入二叉树,感受其中的魅力。 目录 二叉树的顺序结构 堆的概念及结构 堆的实现 堆的创建 堆的初始化与…...

手写一个摸鱼神器:使用python手写一个看小说的脚本,在ide中输出小说内容,同事直呼“还得是你”
文章目录 一、准备python环境二、分析小说网的章节目录三、分析小说网的章节内容四、编写python脚本五、验证一下吧 一、准备python环境 windows从0搭建python3开发环境与开发工具 Python爬虫基础(一):urllib库的使用详解 Python爬虫基础&a…...
【Python 实战】---- 实现批量图片的切割
1. 需求场景 在实际开发中,我们会遇到一种很无聊,但是又必须实现的需求,就是比如协议、大量的宣传页面、大量的静态介绍页面、或者大量静态页面,但是页面高度很高,甚至高度可能会达到50000px,但是为了渲染…...
MAYA粒子基础_场
重力场 牛顿场 径向场 均匀场和重力场的区别 空气场 推动物体 阻力场 推动物体 涡流场 湍流场 体积轴场...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...
