机器学习算法详解3:逻辑回归
机器学习算法详解3:逻辑回归
前言
本系列主要对机器学习上算法的原理进行解读,给大家分享一下我的观点和总结。
本篇前言
本篇对逻辑回归的算法原理进行解读。
目录结构
文章目录
- 机器学习算法详解3:逻辑回归
- 1. 引子
- 2. sigmoid函数
- 3. 原理推导
- 4. 交叉熵损失函数推导
- 4.1 信息熵
- 4.2 KL散度
- 4.3 交叉熵推导
- 4.4 交叉熵损失函数推导
- 5. 为什么选用sigmoid函数?
- 6. 总结
1. 引子
在上一篇提及一个概念广义线性回归,而逻辑回归也是与之相关。
假设我们有一个曲线,如下:

假设它的表达式为y=wx,其中y的值是符合lnx的分布的。那么,可以进行线性映射lny = wx ,变为y=e^(wx),即真正的表达式y=e^(wx)可以变为最初的广义线性形式y=wx(只是此处的y符合lnx分布而已)。
换而言之,我们可以将e^(wx)看作是一个普通的ax,那么逻辑回归就是将这个普通的ax作为某个函数的输入,让函数的输出在[0,1]之间,相当于输出的是概率值,就成了。
2. sigmoid函数
上面提及某函数,那么选择什么样的函数呢?
首先,函数必须满足的要求是:输出值在[0,1]之间。满足这个要求的函数非常多,比如符号函数:

但是,这个函数有一个重要缺点:不是连续可导的(在x=0这个点)。这样会导致我们在优化损失函数的时候,无法直接求导,需要分情况进行求导。其次,这个函数有个小缺点:太僵硬了,只能取1、0这两个值。
针对上述情况,我们提出这个函数要满足的新要求:连续可导,最好是光滑曲线。
那么,前人们找到一个函数,名为 sigmoid函数,公式如下:

函数图像如下:

并且,值得注意的一点是,sigmoid函数的导数非常特殊,其倒数公式如下:

3. 原理推导
基本的导数求法,非常的简单。

4. 交叉熵损失函数推导
4.1 信息熵
要对交叉熵进行推导,首先需要明白什么是信息熵。(本来应该在决策树那里讲的)
熵,大家应该都明白,就是描述一个系统的混乱程度。那么信息熵,就相当于描述一个信息的有用程度。
公式如下:

4.2 KL散度
有时候也称之为KL距离,但是其实并不是真正的距离,因为不符合距离的对称性质。
其衡量两个分布P、Q的相似程度,公式如下:

举个计算的例子:

4.3 交叉熵推导

4.4 交叉熵损失函数推导
该损失函数的推导可以从三个角度入手,分别是sigmoid入手、极大似然估计入手和KL散度入手。这里我接受最后一种推导。
逻辑回归损失函数即衡量真实分布和预测分布的相似性——即KL散度,那么推导过程和上面相似,只是把P and Q换为了y and y^,通过上面可以知道最后的KL散度与交叉熵的值正相关,因此我们可以通过交叉熵构建出损失函数来代替KL散度以衡量真实分布和预测分布的相似程度,即公式:(下面分为两个部分是因为一个为正样本、一个为负样本而已)

5. 为什么选用sigmoid函数?
这个问题也可以这么问:sigmoid函数怎么推出来的?这个是我偶然看视频发现的,我个人觉得有一定的道理,所以在这里分享一下:
对于真实大数据场景,数据的每个特征基本都符合正太分布,并且一般标准差相同而均值不同(感觉上是对的,但是没有证明),那么如下图推导过程:

6. 总结
本篇讲解了逻辑回归的原理,逻辑回归主要应用于二分类任务,也是分类任务中常用的一个算法。
下一篇,讲解支持向量机算法。
相关文章:

机器学习算法详解3:逻辑回归
机器学习算法详解3:逻辑回归 前言 本系列主要对机器学习上算法的原理进行解读,给大家分享一下我的观点和总结。 本篇前言 本篇对逻辑回归的算法原理进行解读。 目录结构 文章目录 机器学习算法详解3:逻辑回归1. 引子2. sigmoid函数3. 原…...

linux命令集合
cd:切换文件路径 pwd:显示当前所处的路径 mkdir:创建目录比如mkdir test touch:创建一个空文件touch test.txt in:用于指定文件夹在另一个位置建立同步的链接in -s /lib/test1 /user/lj 在user目录下建立指向/lib/test1 目录的lj文件 cat:cat file(查看文件内…...

实现卓越供应链:RFID技术的革命性应用
在现代制造业中,供应链和物流的高效运作至关重要,它不仅影响着生产效率,还直接关系到企业的竞争力和客户满意度。为了应对这些挑战,越来越多的企业开始关注智能制造RFID智能设备,将其应用于供应链和物流管理࿰…...

从JVM角度看继承
从JVM角度看继承 最近重读了周志明老师的《深入理解JAVA虚拟机》一书,看完大有收获,但仍对继承情况下对象内存布局有所疑惑,所以查阅资料,结合本书进行分析 参考文档: 【深入理解JVM】:Java类继承关系中…...

基于Python和mysql开发的看图猜成语微信小程序(源码+数据库+程序配置说明书+程序使用说明书)
一、项目简介 本项目是一套基于Python和mysql开发的看图猜成语微信小程序,主要针对计算机相关专业的正在做毕设的学生与需要项目实战练习的Python学习者。 包含:项目源码、项目文档、数据库脚本等,该项目附带全部源码可作为毕设使用。 项目都…...
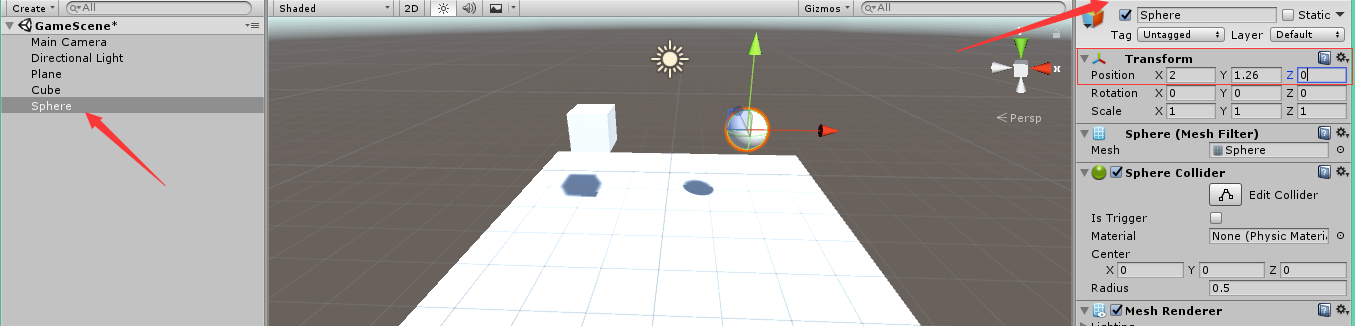
Unity入门教程||创建项目(上)
一、介绍 目的:通过尝试制作一款使用玩家角色把小球弹飞的简单小游戏,熟悉使用Unity进行游戏开发的基本流程。 软件环境:Unity 2017.3.0f3,Visual Studio 2013 二、创建新项目 1,启动Unity后将出现一个并列显示Pro…...

Openbmc编译
1.网址的问题解决 原文 Modifying /conf/local.conf was the only solution that worked for me. Simply add one of the two options:#check connectivity using google CONNECTIVITY_CHECK_URIS "https://www.google.com/"#skip connectivity checks CONNECTIVI…...

美国CN2服务器速度怎么样
美国服务器以免备案、大带宽、性价比高的优势,多用于企业、电商、外贸、视频等个中大型网站建设。但是,因中美服 务器接口原因,导致某些服务器的网络并不稳定,这时候就会对美国服务器产品失望,解决这种问题的方法就是选…...
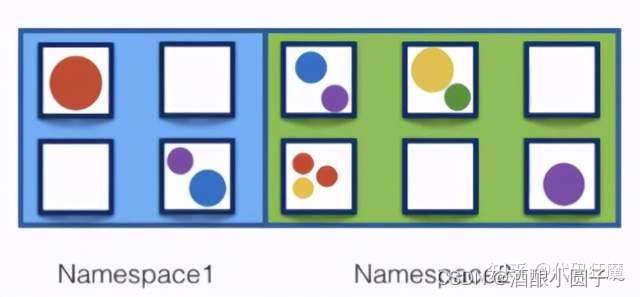
K8S原理架构与实战教程
文章目录 一、背景1.1 物理机时代、虚拟机时代、容器化时代1.2 容器编排的需要 二、K8S架构2.2 Worker节点 三、核心概念3.1 Pod3.2 Deployment3.3 Service3.4 Volume3.5 Namespace 四、K8S安装五、kubectl常用命令六、K8S实战6.1 水平扩容6.2 自动装箱6.2.1 节点污点6.2.2 Pod…...

基于C#的图书管理系统数据库设计报告
第一章 问题描述 1.1 图书管理系统简介 本系统利用.NET处理数据库的功能,实现对图书馆信息的管理。主要功能为管理有关读者、出版社、书籍、借阅和管理者的信息等。 本系统的结构分为读者信息管理模块、出版社信息管理模块、书籍信息管理模块、借阅信息管理模块、…...

【Express.js】pm2进程管理
pm2进程管理 本节我们将介绍如何使用 pm2 运行和监管我们的 express 项目 准备工作 一个 express 项目全局安装 pm2 npm install -g pm2pm2使用介绍 启动应用 你可以用纯命令去运行一个node项目,假设原本运行项目使用 node src/index.js可以跑起来一个项目&am…...
Nginx部署前后端分离项目(Linux)
Nginx代理前端页面、后端接口 一、前端打包二、后端打包三、Linux部署Nginx启动、暂停、重启服务器部署文件地址: 一、前端打包 npm run build二、后端打包 通过Maven 使用package打包 三、Linux部署 安装Nginx 安装环境 yum -y install gcc pcre pcre-devel z…...

Docker网络
1 简介 网络原理 下载iproute工具(linux)ip addr查看地址映射 容器内ip地址会进行映射符号。docker分配的地址。 77: eth0if78: <BROADCAST,MULTICAST,UP,LOWER_UP> mtu 1500 qdisc noqueue state UP group default link/ether 02:42:ac:11:00:…...
第15章_瑞萨MCU零基础入门系列教程之Common I2C总线模块
本教程基于韦东山百问网出的 DShanMCU-RA6M5开发板 进行编写,需要的同学可以在这里获取: https://item.taobao.com/item.htm?id728461040949 配套资料获取:https://renesas-docs.100ask.net 瑞萨MCU零基础入门系列教程汇总: ht…...
《TCP/IP网络编程》阅读笔记--多播与广播
目录 1--多播 2--多播代码实例 3--广播 4--广播代码实例 1--多播 多播方式的数据传输是基于 UDP 完成的,多播数据包的格式与 UDP 数据包相同; 多播与 UDP 的区别:UDP 数据传输以单一目标进行,多播数据同时传递到加入ÿ…...

聚观早报|华为Mate 60 Pro支持面容支付;特斯拉重回底特律车展
【聚观365】9月8日消息 华为Mate 60 Pro已支持面容支付 特斯拉将重回底特律车展 iPhone在美国有1.67亿用户 韩国半导体8月份出口85.6亿美元 比亚迪元PLUS冠军版将于9月15日上市 华为Mate 60 Pro已支持面容支付 毫无预热的华为Mate 60 Pro突然在华为商城首批开售…...

本地缓存Caffeine的缓存过期淘汰策略
本地缓存是一种将数据存储在应用程序的内存中,以加速数据访问的技术。缓存的数据可以是频繁访问的数据,以减少对慢速数据源(如数据库或网络)的访问。缓存通常有一些缓存过期淘汰策略,以确保缓存中的数据保持最新和有效…...
激光焊接汽车尼龙塑料配件透光率测试仪
激光塑性成型技术是近年来塑性加工界出现的一种新技术。通常塑料主要是通过加热加压依赖模具成型。这对于单品种、大批量生产是有效的;而对于各种不同形状的塑料制件则需要昂贵的模具‚装置也较庞大。 高度聚焦的激光束垂直照射在待变形的板料上‚由于塑料直接吸收激…...

2023年高校大数据实验室建设方案
大数据实验室建设方案具体内容包括:人才培养方案建设、课程资源建设、师资建设、实验室建设、教学服务建设。 泰迪打造国内领先的大数据人工智能及课程资源,包括:商务数据分析实训管理平台、云计算资源管理平台、大数据编程实训平台、商务数据…...
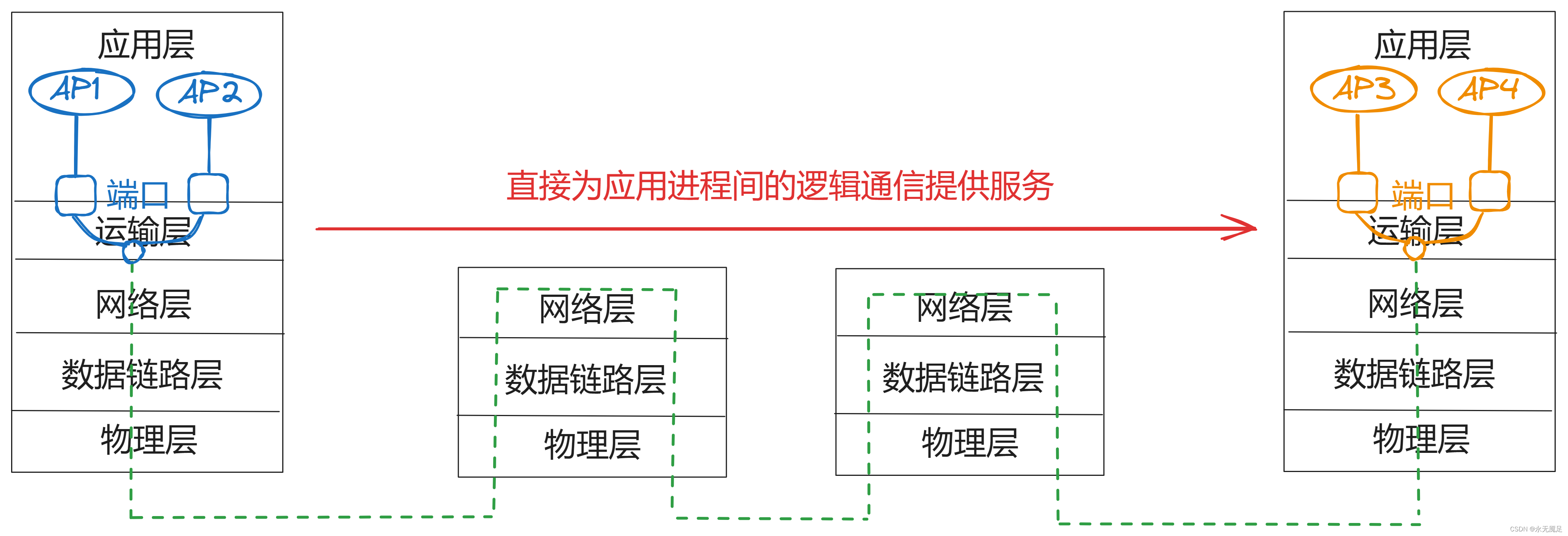
计网第五章(运输层)(一)
在前面的博客中,总是说主机之间进行通信。但实际上通信的真正的实体是位于通信两端主机中的进程。 一、运输层基本概述 运输层的任务就是为运行在不同主机上的应用进程提供直接的通信服务,运输层的协议又称为端到端协议。运输层中使用不同的端口来对应…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
