【力扣周赛】第 361 场周赛(⭐前缀和+哈希表 树上倍增、LCA⭐)
文章目录
- 竞赛链接
- Q1:7020. 统计对称整数的数目
- 竞赛时代码——枚举预处理
- Q2:8040. 生成特殊数字的最少操作(倒序遍历、贪心)
- 竞赛时代码——检查0、00、25、50、75
- Q3:2845. 统计趣味子数组的数目
- 竞赛时代码——前缀和+哈希表
- 相似题目——1590. 使数组和能被 P 整除(确实很相似的题目)
- Q4:2846. 边权重均等查询⭐⭐⭐⭐⭐
- 读题
- 解法——树上倍增、最近公共祖先LCA
- 相关题目
- 成绩记录
竞赛链接
https://leetcode.cn/contest/weekly-contest-361/
Q1:7020. 统计对称整数的数目
https://leetcode.cn/problems/count-symmetric-integers/
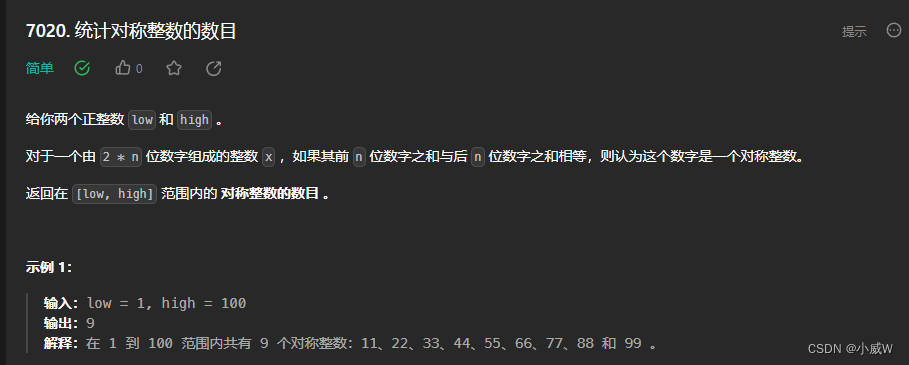
提示:
1 <= low <= high <= 10^4
竞赛时代码——枚举预处理
预处理所有数字是否为对称整数。
cnt[i]表示 <=i 的数字中有几个对称整数。
class Solution {static int[] cnt = new int[10005];// 预处理static {for (int i = 1; i <= 10001; ++i) {cnt[i] = cnt[i - 1];if (op(i)) cnt[i]++;}}public int countSymmetricIntegers(int low, int high) {return cnt[high] - cnt[low - 1];}// 判断x是否为对称整数public static boolean op(int x) {List<Integer> ls = new ArrayList<>();while (x != 0) {ls.add(x % 10);x /= 10;}int n = ls.size();if (n % 2 == 1) return false;int a = 0, b = 0;for (int i = 0; i < n; ++i) {if (i < n / 2) a += ls.get(i);else b += ls.get(i);}return a == b;}
}
Q2:8040. 生成特殊数字的最少操作(倒序遍历、贪心)
https://leetcode.cn/problems/minimum-operations-to-make-a-special-number/
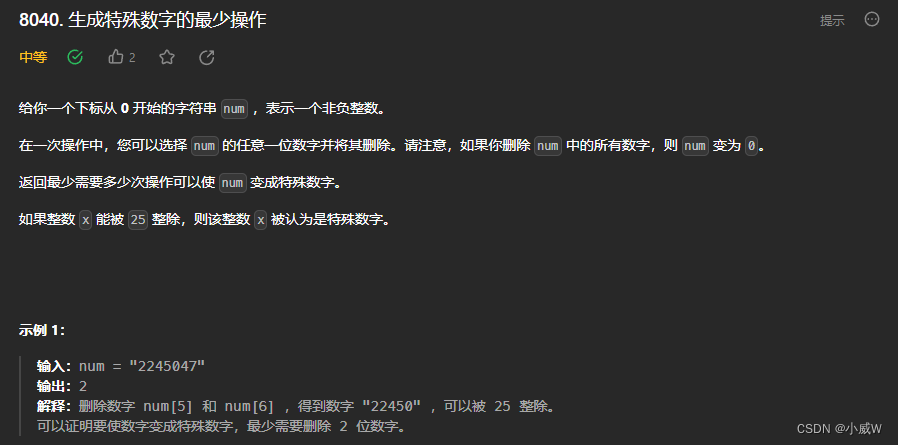
提示
1 <= num.length <= 100
num 仅由数字 '0' 到 '9' 组成
num 不含任何前导零
竞赛时代码——检查0、00、25、50、75
检查位置最靠后的 00、25、50、75 的位置。
如果都不存在但是有 0 的话,答案则为 n - 1。(因为 0 可以不删)
class Solution {public int minimumOperations(String num) {int n = num.length();boolean f0 = false, f5 = false;for (int i = n - 1; i >= 0; --i) {char ch = num.charAt(i);if (ch == '0') {if (f0) return n - i - 2; // 检查00f0 = true;} else if (ch == '5') {if (f0) return n - i - 2;; // 检查50f5 = true;} else if (ch == '2' || ch == '7') {if (f5) return n - i - 2;; // 检查25,75}}if (f0) return n - 1; // 检查是否有0return n;}
}
Q3:2845. 统计趣味子数组的数目
https://leetcode.cn/problems/count-of-interesting-subarrays/
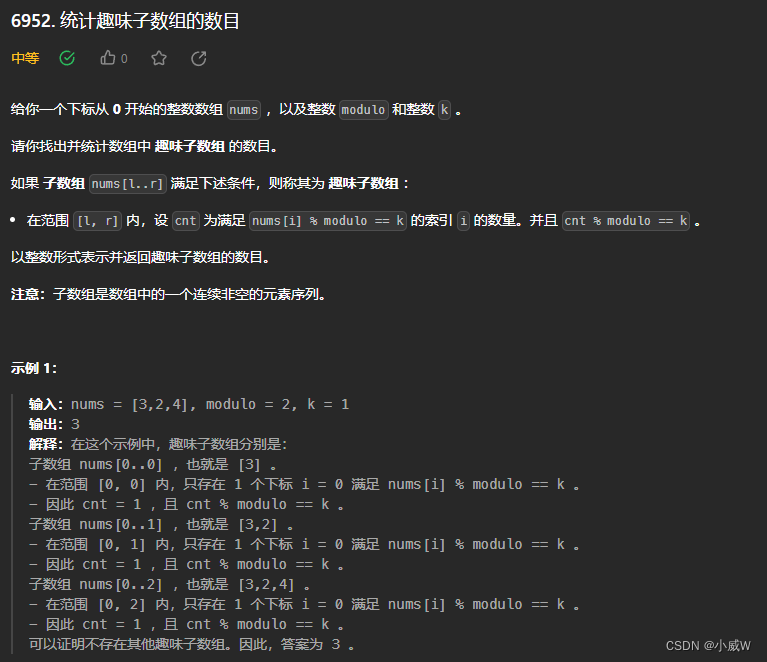
提示:
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^9
1 <= modulo <= 10^9
0 <= k < modulo
竞赛时代码——前缀和+哈希表
使用前缀和数组可以快速求出从 l ~ r 之间满足要求的元素个数 cnt。
求出前缀和数组之后,从前往后依次枚举下标。对于当前的前缀和 sum[r],前面有若干个满足 (sum[r] - sum[x]) % modulo == k 的下标,这些下标的共同特征是:它们的值 sum[x] = (sum[r] - k + modulo) % modulo。
在枚举的过程中用哈希表 cnt 记录下各种 sum[i] 数值的数量,即 cnt[[sum[i]]++。
这样当枚举到 当前的前缀和为 sum[r] 时,与他相匹配的前缀和设为 x,则有 (sum[r] - x) % modulo == k,解得 x = (sum[r] - k + modulo) % modulo。 就可以快速找到 sum[r] 之前有几个可以和当前下标配对的下标 l,组成符合条件的区间 l ~ r,从哈希表中可以快速找出有 cnt[x] 的值个可以匹配。
即——在 r 之前有 cnt[x] 个下标,分别为 l1、l2…、lx 满足区间 li ~ r 之间的 cnt % modulo == k。
class Solution {public long countInterestingSubarrays(List<Integer> nums, int modulo, int k) {int n = nums.size();int[] x = new int[n], sum = new int[n + 1]; // x是原始数组,sum是前缀和数组Map<Integer, Integer> cnt = new HashMap<>(); // 存储各个余数为key的位置的数量cnt.put(0, 1);long ans = 0;for (int i = 0; i < n; ++i) {if (nums.get(i) % modulo == k) x[i] = 1;sum[i + 1] = (sum[i] + x[i]) % modulo; // 前缀和int r = sum[i + 1];ans += cnt.getOrDefault((r - k + modulo) % modulo, 0);cnt.merge(r, 1, Integer::sum);}return ans;}
}
相似题目——1590. 使数组和能被 P 整除(确实很相似的题目)
https://leetcode.cn/problems/make-sum-divisible-by-p/description/
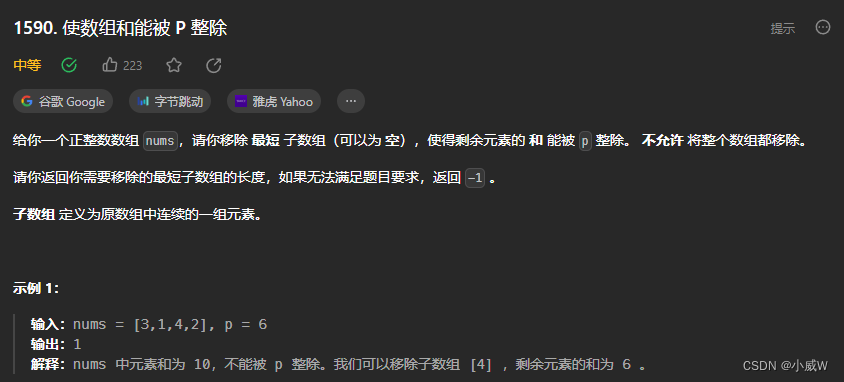
提示:
1 <= nums.length <= 105
1 <= nums[i] <= 109
1 <= p <= 109
class Solution {public int minSubarray(int[] nums, int p) {int n = nums.length;int[] sum = new int[n + 1]; // 前缀和数组for (int i = 0; i < n; ++i) {sum[i + 1] = (sum[i] + nums[i]) % p;}int t = sum[n], ans = n;if (t == 0) return 0;Map<Integer, Integer> idx = new HashMap<>(); // 记录各个前缀和出现的下标idx.put(0, -1);for (int i = 0; i < n; ++i) {// x是当前前缀和,y是和x配对组成t的前缀和int x = sum[i + 1], y = (x - t + p) % p; // 如果之前有y,就尝试更新答案 if (idx.containsKey(y)) ans = Math.min(ans, i - idx.get(y));idx.put(x, i);}return ans == n? -1: ans;}
}
Q4:2846. 边权重均等查询⭐⭐⭐⭐⭐
https://leetcode.cn/problems/minimum-edge-weight-equilibrium-queries-in-a-tree/
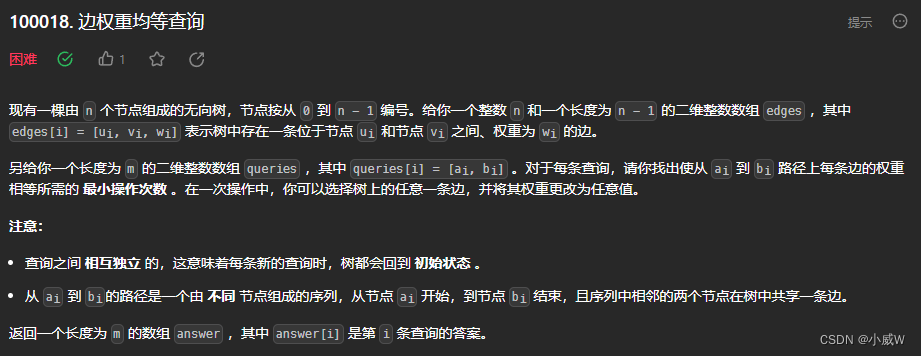
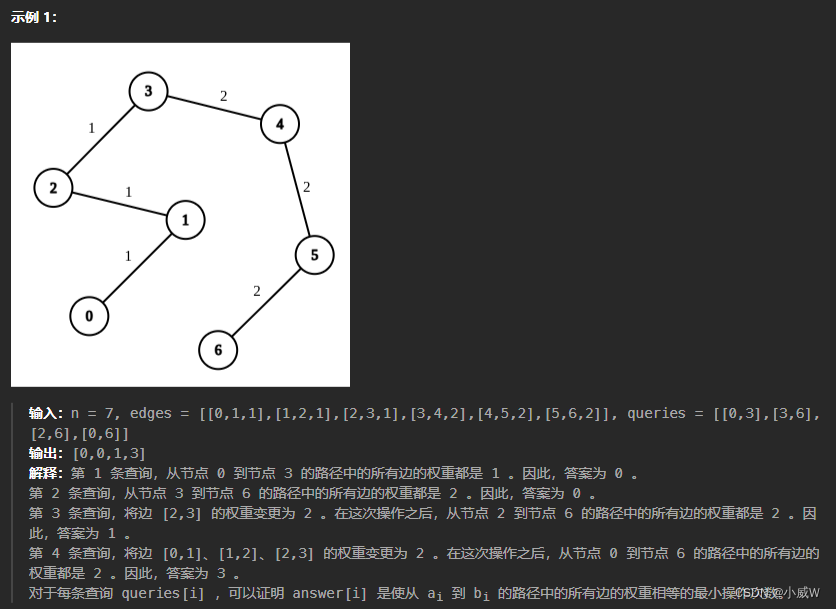
提示:
1 <= n <= 10^4
edges.length == n - 1
edges[i].length == 3
0 <= ui, vi < n
1 <= wi <= 26
生成的输入满足 edges 表示一棵有效的树
1 <= queries.length == m <= 2 * 10^4
queries[i].length == 2
0 <= ai, bi < n
读题
给了一个 n 个节点的无向图。
每次查询,给两个点 a ,b。求 a 和 b 路径之间的所有边权,都变成相等需要操作几步——实际上是求 a 和 b 之间有几条边,其中出现次数最多的边权出现了几次。
解法——树上倍增、最近公共祖先LCA
关于这部分的知识点总结可见:【算法】树上倍增 & LCA
https://leetcode.cn/problems/minimum-edge-weight-equilibrium-queries-in-a-tree/solutions/2424060/lca-mo-ban-by-endlesscheng-j54b/

思路总结:
用树上倍增的思想维护:各个节点的深度、各个节点和父节点之间各种边权的数量。
求答案时,先将两个节点放在同一深度,实现方法是 y 先跳 d[y] - d[x] 的深度。
然后,x 和 y 一起往上跳。
class Solution {public int[] minOperationsQueries(int n, int[][] edges, int[][] queries) {// 临界表存储无向图List<int[]>[] g = new ArrayList[n]; Arrays.setAll(g, e -> new ArrayList<>());for (int[] e: edges) {int x = e[0], y = e[1], w = e[2] - 1;g[x].add(new int[]{y, w});g[y].add(new int[]{x, w});}int m = 32 - Integer.numberOfLeadingZeros(n); // n的二进制长度int[][] pa = new int[n][m]; // pa[x][i]表示节点x的第2^i个父节点for (int i = 0; i < n; ++i) {Arrays.fill(pa[i], -1); // -1表示没有这个父节点}int[][][] cnt = new int[n][m][26]; // cnt[x][i][w]记录节点x和父节点之间的边权为w的个数int[] depth = new int[n]; // 记录n个节点的深度// 使用 dfs 从0节点开始 初始化pa、cnt 计算depthdfs(0, -1, g, pa, cnt, depth);// 计算 pa 和 cnt// 先枚举i,(也就是先算出所有节点的爷爷、再求所有节点爷爷的爷爷...for (int i = 0; i < m - 1; ++i) { // 先枚举i,范围是0~m-2for (int x = 0; x < n; ++x) { // 再枚举xint p = pa[x][i]; // 取出节点x的第2^i个父节点if (p != -1) { int pp = pa[p][i]; // 取出节点x的第2^i个父节点的第2^i个父节点pa[x][i + 1] = pp; // 赋值——x的第2^(i+1)个父节点// 通过cnt[x][i]和cnt[p][i]计算 cnt[x][i+1]for (int j = 0; j < 26; ++j) {cnt[x][i + 1][j] = cnt[x][i][j] + cnt[p][i][j];}}}}// 计算答案int[] ans = new int[queries.length];for (int qi = 0; qi < queries.length; qi++) { // 枚举每一个查询int x = queries[qi][0], y = queries[qi][1];int pathLen = depth[x] + depth[y]; // x的深度和y的深度int[] cw = new int[26]; // 统计各种边权在x和y之间出现的次数// 让 x 作为深度更小的那个节点if (depth[x] > depth[y]) {int t = x;x = y;y = t;}// 让 y 和 x 在同一深度(先让 y 跳 depth[y]-depth[x])for (int k = depth[y] - depth[x]; k > 0; k &= k - 1) {int i = Integer.numberOfTrailingZeros(k);int p = pa[y][i];for (int j = 0; j < 26; ++j) {cw[j] += cnt[y][i][j];}y = p;}// y和x位于同一深度的时候可能位于同一个节点,那么就不用继续计算了if (y != x) {// 让 x 和 y 同时往上跳for (int i = m - 1; i >= 0; i--) { // 从大到小尝试各种2^i跳法int px = pa[x][i], py = pa[y][i];// 如果px!=py,说明可以跳if (px != py) {for (int j = 0; j < 26; ++j) {cw[j] += cnt[x][i][j] + cnt[y][i][j];} x = px;y = py;}}// 因为跳到最后,x和y都是最近公共祖先的直系节点,所以px一定会=py// 手动计算cnt[j]for (int j = 0; j < 26; ++j) {cw[j] += cnt[x][0][j] + cnt[y][0][j];}x = pa[x][0]; // x此时变成了 x 和 y 的最近公共祖先}int lca = x;pathLen -= depth[lca] * 2;int maxCw = 0;for (int i = 0; i < 26; ++i) maxCw = Math.max(maxCw, cw[i]);ans[qi] = pathLen - maxCw;}return ans;}public void dfs(int x, int fa, List<int[]>[] g, int[][] pa, int[][][] cnt, int[] depth) {pa[x][0] = fa; // 父节点for (int[] e: g[x]) { // 枚举和x相连的每一条边int y = e[0], w = e[1];if (y != fa) {cnt[y][0][w] = 1;depth[y] = depth[x] + 1;dfs(y, x, g, pa, cnt, depth);}}}
}
相关题目
1483. 树节点的第 K 个祖先
2836. 在传球游戏中最大化函数值
成绩记录

喜报!应该要升 guardian 了!
相关文章:

【力扣周赛】第 361 场周赛(⭐前缀和+哈希表 树上倍增、LCA⭐)
文章目录 竞赛链接Q1:7020. 统计对称整数的数目竞赛时代码——枚举预处理 Q2:8040. 生成特殊数字的最少操作(倒序遍历、贪心)竞赛时代码——检查0、00、25、50、75 Q3:2845. 统计趣味子数组的数目竞赛时代码——前缀和…...
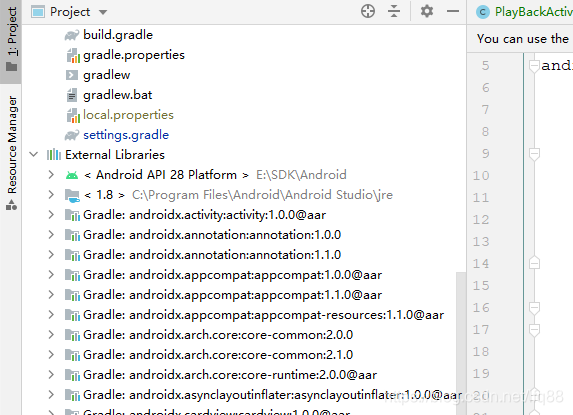
解决 Android 依赖冲突
解决办法 问题原因就是,各个模块所有的依赖(递归)的 jar 包最后都会加载到安卓的项目中,你可以选择 project 形式查看 External Libraries,都在这了。所以解决问题关键就是干掉冲突,剩下一个就行了…...
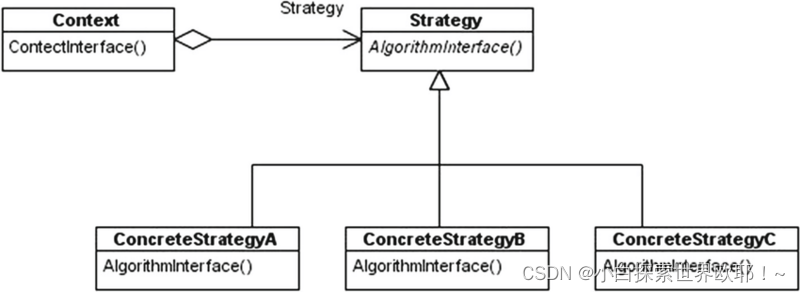
前端设计模式基础笔记
前端设计模式是指在前端开发中经常使用的一些解决问题的模式或思想。它们是经过实践证明的最佳实践,可以帮助我们更好地组织和管理我们的代码。 一、单例模式(Singleton Pattern) 单例模式是一种创建型模式,它保证一个类只有一个…...

Python项目开发:Flask基于Python的天气数据可视化平台
目录 步骤一:数据获取 步骤二:设置Flask应用程序 步骤三:处理用户输入和数据可视化 步骤四:渲染HTML模板 总结 在这个数字化时代,数据可视化已经成为我们理解和解释信息的重要手段。在这个项目中,我们…...

Dell 服务器常见报错信息汇总
Dell 服务器常见报错汇总 如果有别的报错信息欢迎补充...

算法通关村-----贪心面试大热门之区间问题
判断区间是否重叠 问题描述 给定一个会议时间安排数组intervals,每个会议时间都包括开始时间和结束时间,intervals[i] [starti,endi],请你判断一个人是否能够参加这里面的全部会议。详见leetcode252 问题分析 先将会议安排数组按照开始时间排序&…...

OAK相机:自动或手动设置相机参数
OAK相机:自动或手动设置相机参数 硬件软件 硬件 使用硬件如下: 4✖️ov9782相机OAK-FFC-4P驱动板 硬件接线参考博主的一篇博客:OAK相机:多相机硬件同步拍摄 软件 博主使用的是Ubuntu18.04系统,首先配置所需的pytho…...

百家宴焕新上市,持续深耕100-300元价位段
执笔 | 尼 奥 编辑 | 古利特 4月8日,长江酒道曾在《百家宴谋划“晋级”之路,多措并举切分宴席市场“蛋糕”》一文中提到:“百家宴主力新品即将登场,市场政策灵活焕新。” 如今,百家宴新品及市场新政,正…...

Linux Debian12使用git将本地项目上传到码云(gitee)远程仓库
一、注册码云gitee账号 这个可以参考其他教程,本文不做介绍。 gitee官网:https://gitee.com/ 二、Linux Debian12安装git 如果Linux系统没有安装git,可以使用下面命令安装git sudo apt install git 三、gitee新建仓库 我这只做测试&…...

电子烟行业常用的英文表达
1. 电子烟的各种表达 a) 电子烟 i. Electronic-cigarette, ii. Electronic smoke, iii. electronic cigarettes iv. Electric cigarette, v. E-Cigarettes vi. e-cigarette, vii. e-Cig viii. E cigar,e-cigar 电子烟雪茄 2. 电子烟特指词汇及衍生 a) VAPE i. Vapo…...

【SpringMvc 丨跨域】
Spring MVC 支持跨域处理(CORS)。 CORS 简介处理CORS 过滤器CrossOrigin注解java配置xml配置 主页传送门:📀 传送 简介 跨域是指在浏览器的同源策略下,不能执行其他网站的脚本。它是由浏览器的安全限制造成的…...

【C语言】【strlen函数的使用与模拟实现】
1.strlen函数的使用和模拟实现 1.1使用: size_t strlen(const char* str)返回类型为无符号整型,参数是字符指针 计算的是字符串中到“\0"之前的字符个数 1.2模拟实现: 方法一:计数器式遍历 #include<stdio.h> #in…...

类和对象【基础概念】
全文目录 类的定义定义方式 类的访问限定符封装(面向对象的三大特性之一) 类对象模型类对象的存储方式类对象的大小计算 this指针this指针的特性**this指针可以为空吗?** 类的定义 在C中,C语言中的结构体struct中除了定义变量外还…...
)
如何测试生成式人工智能(AIGC)
简介:在人工智能日趋普及的今天,生成式人工智能(AIGC)已经成为不可忽视的一个分支。从自动化生成新闻、编写代码到图像和音频生成,AIGC几乎无处不在。但如何确保这些生成的内容达到预期标准、安全可靠,同时…...

机器学习算法详解3:逻辑回归
机器学习算法详解3:逻辑回归 前言 本系列主要对机器学习上算法的原理进行解读,给大家分享一下我的观点和总结。 本篇前言 本篇对逻辑回归的算法原理进行解读。 目录结构 文章目录 机器学习算法详解3:逻辑回归1. 引子2. sigmoid函数3. 原…...

linux命令集合
cd:切换文件路径 pwd:显示当前所处的路径 mkdir:创建目录比如mkdir test touch:创建一个空文件touch test.txt in:用于指定文件夹在另一个位置建立同步的链接in -s /lib/test1 /user/lj 在user目录下建立指向/lib/test1 目录的lj文件 cat:cat file(查看文件内…...

实现卓越供应链:RFID技术的革命性应用
在现代制造业中,供应链和物流的高效运作至关重要,它不仅影响着生产效率,还直接关系到企业的竞争力和客户满意度。为了应对这些挑战,越来越多的企业开始关注智能制造RFID智能设备,将其应用于供应链和物流管理࿰…...

从JVM角度看继承
从JVM角度看继承 最近重读了周志明老师的《深入理解JAVA虚拟机》一书,看完大有收获,但仍对继承情况下对象内存布局有所疑惑,所以查阅资料,结合本书进行分析 参考文档: 【深入理解JVM】:Java类继承关系中…...

基于Python和mysql开发的看图猜成语微信小程序(源码+数据库+程序配置说明书+程序使用说明书)
一、项目简介 本项目是一套基于Python和mysql开发的看图猜成语微信小程序,主要针对计算机相关专业的正在做毕设的学生与需要项目实战练习的Python学习者。 包含:项目源码、项目文档、数据库脚本等,该项目附带全部源码可作为毕设使用。 项目都…...
Unity入门教程||创建项目(上)
一、介绍 目的:通过尝试制作一款使用玩家角色把小球弹飞的简单小游戏,熟悉使用Unity进行游戏开发的基本流程。 软件环境:Unity 2017.3.0f3,Visual Studio 2013 二、创建新项目 1,启动Unity后将出现一个并列显示Pro…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
