算法通过村第六关-树青铜笔记|中序后序
文章目录
- 前言
- 1. 树的常见概念
- 2. 树的性质
- 3. 树的定义与存储方式
- 4. 树的遍历方式
- 5. 通过序列构建二叉树
- 5.1 前中序列恢复二叉树
- 5.2 中后序列恢复二叉树
- 总结
前言
提示:瑞秋是个小甜心,她只喜欢被爱,不懂的去爱人。 --几米《你们 我们 他们》
树是一种非常重要的数据结构,在算法和工程中都有大量的应用,我们这里从概念一步一步学习,闯过这一关,掌握树的基本特征以及遍历方面的基础问题。
1. 树的常见概念
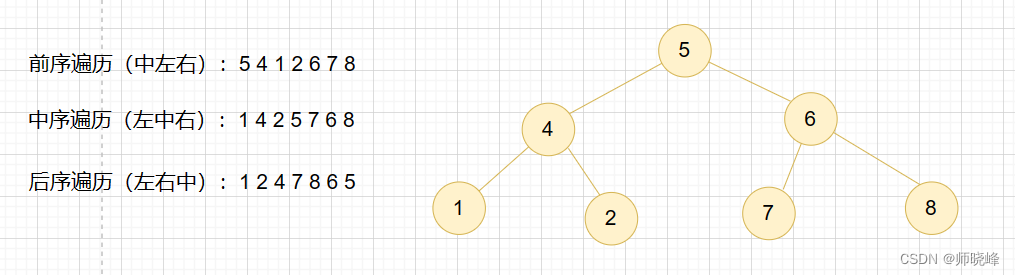
树是一个有n个有限节点组成一个具有层次关系的集合,每个节点有0个或者多个子节点,没有父节点的节点为称为根节点,也就是说除了根节点以为每个节点都有父节点,并且有且只有一个节点。树的种类有很多,最常见的就是二叉树了,基本结构如下:
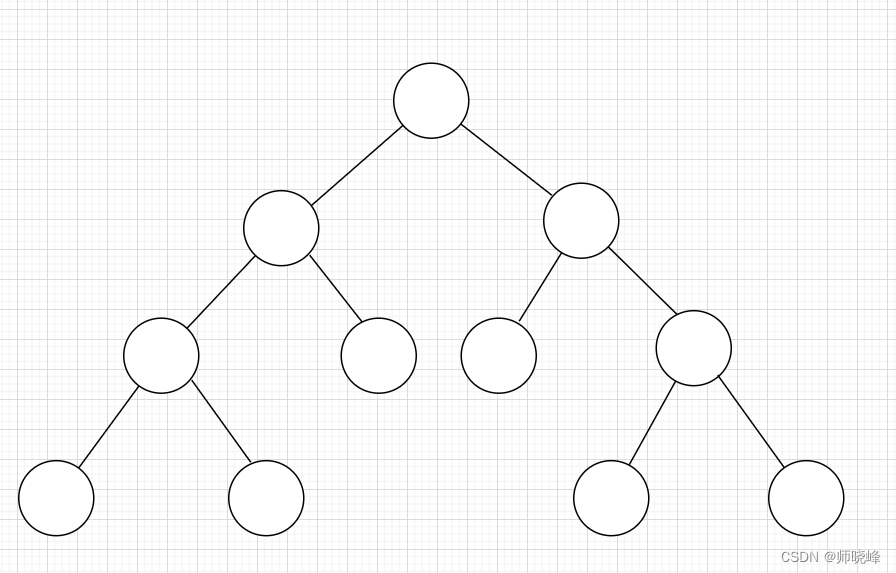
参考上面图的结构,可以很方面的理解树的概念:
- 节点的度:一个节点含有的几点的个数称为该节点的度
- 树的度:一颗树中,最大的节点的度称为树的度,注意与节点度的区别
- 叶节点或者终端节点:度为0的节点称为叶节点
- 非终端节点或者分支节点:度不为0的节点
- 双亲节点或者父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点
- 孩子节点或者子节点:一个节点含有的子树的根节点称为该节点的子节点
- 兄弟节点:具有相同父节点的节点互称为兄弟节点
- 节点的祖先:从根节点到该节点所有分支上的所有节点
- 子孙:以某节点为根节的子树中任一节点都称为该节点的子孙
- 森林:有m(m >= 0 )课互不相交的树的集合称为森林
- 无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树
- 有序树:树中任意节点的子节点之间有顺序关系,这种树称为有序树
- 二叉树:每个节点最多含有两个子树的树称为二叉树
2. 树的性质
- 性质1:在二叉树的第i层上至多有2^(i - 1)个节点(i > 0)
- 性质2:深度为k的二叉树之多有2^k - 1 个节点(k > 0)
- 性质3:对于任意一颗二叉树,如果其叶节点数为N0,而度数为2的节点总数为N2,则N0 = N2 + 1
- 性质4:具有n个节点的完全二叉树的深度必为log2(n + 1)
- 性质5:对完全二叉树,若从上至下,从左至右编号,则编号为i的节点,其左孩子的编号一定是2i,其右孩子必是2i+ 1;其双亲的编号是i/2(i == 1 时为根,除外哈🤣)
满二叉树和完全二叉树是经常晕的问题,我们有必要单独看一下,满二叉树就是如果一棵二叉树只有度为0的节点和度为2的节点,而且度为0的节点在同一层,则这棵二叉树为满二叉树。
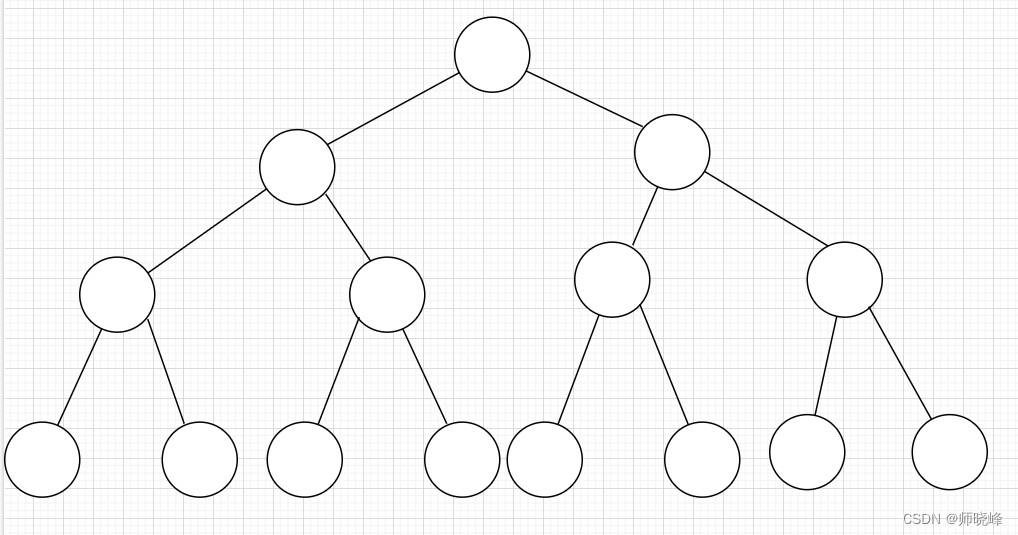
这颗二叉树为满二叉树,也可以说深度为k=4,有2^k -1 = 15个 节点的二叉树。
完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没有填满外,其余每层节点点数都达到最大值,并且最下面一层的节点都集中在该层的最左侧的若干位置。
这个定义,就有些恶心了,估计大部分看了之后还是不懂什么是完全二叉树,看看下面的图:
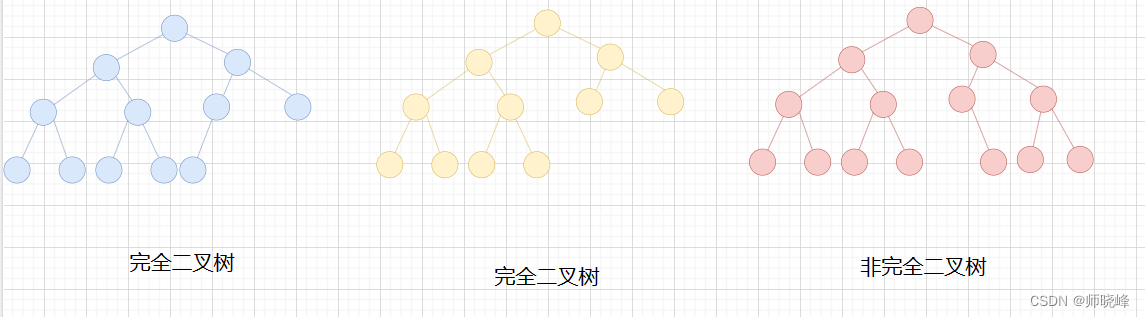
前面两棵树的前n-1层都是满的,最后一层所有子节点都集中在左侧区域,而且节点之间不能有间隙。最后一个为什么呢?他有一个节点缺少一个左子节点/
3. 树的定义与存储方式
注意:
这里我们主要看原理,不执行代码,采用伪代码的方式,理解方便一些
定义树的原理和前面讲的链表本质上差不多,只不过多了一个指针,如果是二叉树的化,只要在链表上的定义增加一个指针就可以了:
public class TreeNode{int val;TreeNode left;TreeNode right;
}
这里本质上就是两个引用,分别指向两个位置,为了方便理解,我们称为左孩子和右孩子。如果是N叉树要如何定义呢?其实就是每个节点最多可以有N个节点指向其他位置,这里就不用left和right,我们使用List存储就行了,也就是如下:
// 定义N叉树
public class TreeNode {int val;List<TreeNode> nodes;
}
那么是否可以采用数组的方式存储二叉树呢?其实就是用数组来存储二叉树的,顺序存储的方式如图:
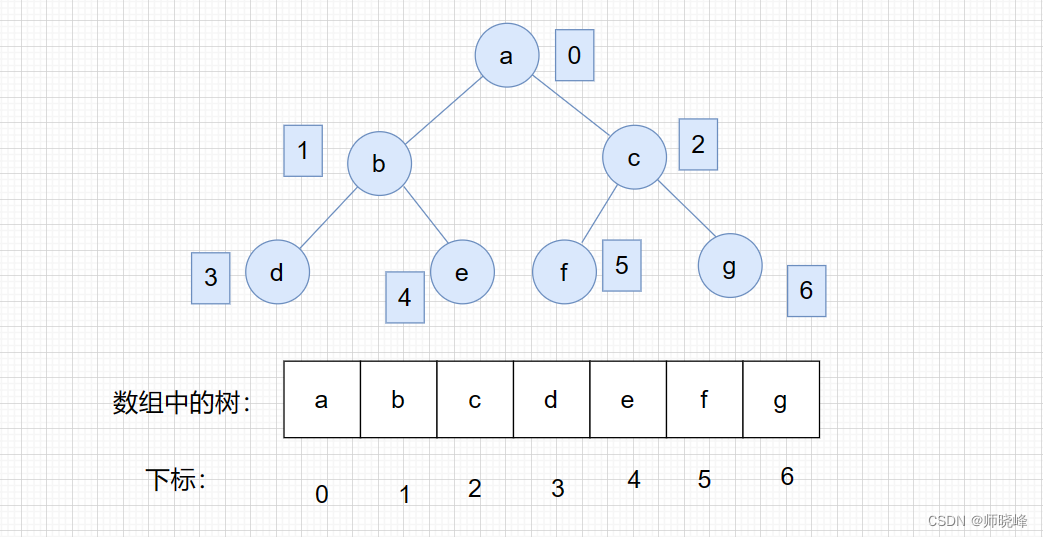
用数组来存储二叉树如何遍历呢?如果父节点的数组下标i,那么它的做还是就是 i* 2 + 1,右孩子就是 i * 2 + 2.
但是用链式表示二叉树,更方便我们理解,所以一般也采用链式二叉树。所以大家要知道一点,数组也是可以便是二叉树的。
使用数组存储的最大问题就是可能存在大量的空间浪费。如图上面假设b没有分支,那么数组1 3 4就空着,但是整个数组的大小仍然是7,因此很少使用数组来存储树。
4. 树的遍历方式
我们常见的树的遍历方式,层次遍历和深度优先遍历两种:
- 深度优先遍历:先往深走,遇到叶子节点再往回走
- 广度优先遍历:一层一层的去遍历,一层遍历完再访问下一层
这两种遍历方式不仅仅是二叉树,N叉树也是,图结构也有,我们更常见的叫法:广度优先和深度优先,本质上是一回事。深度优先又有前中后三种,避免混淆,我们记住一点:前指的是中间的父节点再遍历中的顺序,只要明白了这一点,前中后序就是指中间节点的位置就可以了。
看如下中间节点的顺序,就可以发现问题,访问中间节点的顺序就是所谓的遍历方式
前序遍历:中左右
中序遍历:左中右
后序遍历:左右中
大家试着画图写一写,看看自己是否真的理解前中后序了。
后面大量的算法都与这四种(层次,前中后)遍历方式有关,有的题目根据处理角度不同,可以用层次遍历,也可以用一种甚至两种深度优先的方式来实现。
5. 通过序列构建二叉树
前面我们已经介绍了怎么些前中后序的过程,这里我们看一看怎么通过序列来恢复原始二叉树:
前序遍历:中左右 [5 4 1 2 6 7 8]
中序遍历:左中右 [1 4 2 5 7 6 8]
后序遍历:左右中 [1 2 4 7 8 6 5]
5.1 前中序列恢复二叉树
我们先看看如何通过中前序列恢复二叉树:
前序遍历:中左右 [5 4 1 2 6 7 8]
中序遍历:左中右 [1 4 2 5 7 6 8]
- 第一轮
我们先从前序第一个就是访问根节点,所以根节点是5
中序遍历的特点是根节点的左子树的元素在根节点左侧,右子树的元素都在根节点右侧,从中序遍历序列我们可以划分成如下结构:
前序序列划分:
5 [ 4 1 2 ] [ 6 7 8 ]
中序序列划分:
[ 1 4 2 ] 5 [ 7 6 8 ]
当然前序序列第一个括号里面的都是左子树的元素,第二个括号一定都是右子树的元素。
那么这里怎么将这两个括号从哪里分开,我们彩照中序的两个数组划分。我们看前序2之前的元素都在第一个括号中,7之后的元素都在第二个数组中,所以这里从2和7之间划分。
由此我们画图表示一下,看下此时的树的结构:

- 第二轮:
我们先看两个序列的第一个数组
根据上面的划分方法:
前序序列划分:
4 [ 1 ] [ 2 ]
中序序列划分:
[ 1 ] 4 [ 2 ]
此时树的结构为:
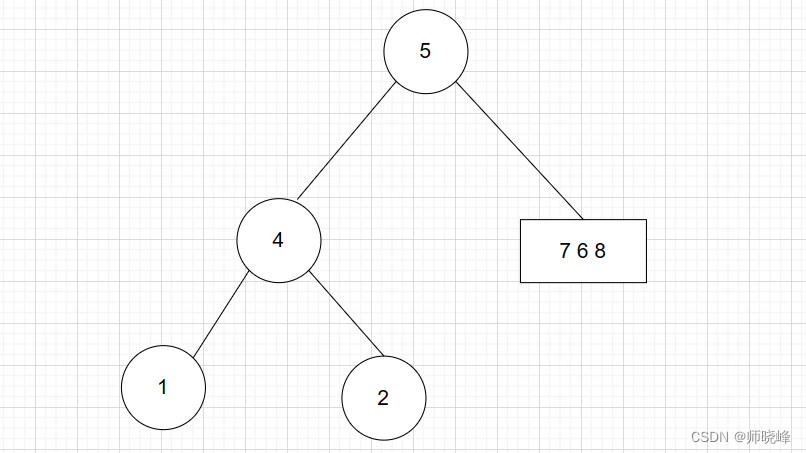
- 第三轮
我们看两个序列的第二个数组
根据上面的划分方法:
前序序列划分:
6 [ 7 ] [ 8 ]
中序序列划分:
[ 7 ] 6 [ 8 ]
此时树的结构为:
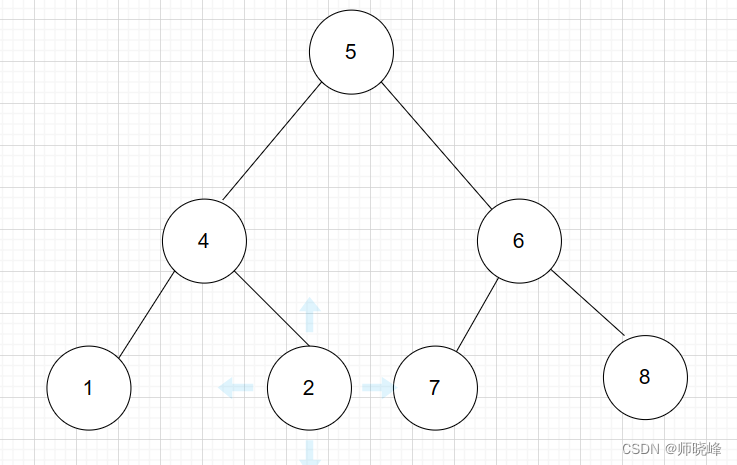
如此就是最终效果了,可以和上面的图对比一下。
5.2 中后序列恢复二叉树
通过中序和后序也能恢复原始序列,唯一不同的是后续的最后一个是根节点,中序的处理上面是一样的过程。
中序遍历:左中右 [1 4 2 5 7 6 8]
后序遍历:左右中 [1 2 4 7 8 6 5]
这里读者可以自行尝试,我这里不做赘述了。
Q&A💡:
那么有疑问了,为什么前序和后序不能恢复二叉树?
前序遍历:中左右 [5 4 1 2 6 7 8]
后序遍历:左右中 [1 2 4 7 8 6 5]
我们看前序和后序,通过前序我们可以知道根节点,通过后序我们也只能知道根节点,那么中间的部分要怎么划分呢?那些元素属于左子树,那些元素属于右子树呢?很显然,我们不得而知,所以用前序和后序不能恢复二叉树。
推荐力扣的题目⭐⭐⭐:
前序和中序造树:105. 从前序与中序遍历序列构造二叉树 - 力扣(LeetCode)
中序和后序造树:106. 从中序与后序遍历序列构造二叉树 - 力扣(LeetCode)
总结
提示:树的概念,二叉树、完全二叉树、满二叉树,树的恢复,前中后序序列
相关文章:

算法通过村第六关-树青铜笔记|中序后序
文章目录 前言1. 树的常见概念2. 树的性质3. 树的定义与存储方式4. 树的遍历方式5. 通过序列构建二叉树5.1 前中序列恢复二叉树5.2 中后序列恢复二叉树 总结 前言 提示:瑞秋是个小甜心,她只喜欢被爱,不懂的去爱人。 --几米《你们 我们 他们》…...

C++动态内存管理+模板
💓博主个人主页:不是笨小孩👀 ⏩专栏分类:数据结构与算法👀 C👀 刷题专栏👀 C语言👀 🚚代码仓库:笨小孩的代码库👀 ⏩社区:不是笨小孩👀 🌹欢迎大…...
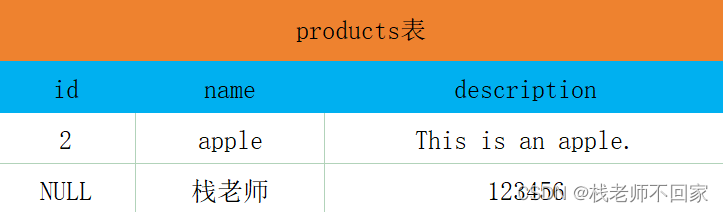
SQL 注入漏洞攻击
文章目录 1. 介绍2. 无密码登录3. 无用户名无密码登录4. 合并表获取用户名密码 1. 介绍 假设你用自己的用户名和密码登录了一个付费网站,网站服务器就会查询一下你是不是 VIP 用户,而用户数据都是放在数据库中的,服务器通常都会向数据库进行查…...

一篇五分生信临床模型预测文章代码复现——Figure 10.机制及肿瘤免疫浸润(四)
之前讲过临床模型预测的专栏,但那只是基础版本,下面我们以自噬相关基因为例子,模仿一篇五分文章,将图和代码复现出来,学会本专栏课程,可以具备发一篇五分左右文章的水平: 本专栏目录如下: Figure 1:差异表达基因及预后基因筛选(图片仅供参考) Figure 2. 生存分析,…...

Transformer 模型中常见的特殊符号
Transformer 模型中常见的特殊符号 通过代码一起理解一下 Transformer 模型中常见的特殊符号, 示例代码, special_tokens{unk_token: [UNK], sep_token: [SEP], pad_token: [PAD], cls_token: [CLS], mask_token: [MASK]}这段代码是定义了一个字典spec…...

C# halcon SubImage的使用
SubImage(HObject imageMinuend, HObject imageSubtrahend, out HObject imageSub, HTuple mult, HTuple add) 公式 x1imageMinuend此行此列的灰度 x2imageSubtrahend此行此列的灰度 则imageSub此行此列的灰度为;(x1-x2)*multadd 溢出裁剪 以byte图为例,小于0&a…...
)
每天几道Java面试题:异常机制(第三天)
目录 第三幕、第一场)异常机制面试题 友情提醒 背面试题很枯燥,加入一些戏剧场景故事人物来加深记忆。PS:点击文章目录可直接跳转到文章指定位置。 第三幕、 第一场)异常机制面试题 【面试官老吉,面试官潘安,面试者…...

Linux 中的 chattr 命令及示例
Linux 中的chattr命令是一个文件系统命令,用于更改目录中文件的属性。该命令的主要用途是使多个文件无法被超级用户以外的用户更改。管理员表示,众所周知,Linux 是一个多用户操作系统,一个用户有可能删除另一个用户非常关心的文件。为了避免这种情况,Linux 提供了“ chatt…...

LeetCode 2605. Form Smallest Number From Two Digit Arrays【数组,哈希表,枚举;位运算】1241
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

VoxWeekly|The Sandbox 生态周报|20230904
欢迎来到由 The Sandbox 发布的《VoxWeekly》。我们会在每周发布,对上一周 The Sandbox 生态系统所发生的事情进行总结。 如果你喜欢我们内容,欢迎与朋友和家人分享。请订阅我们的 Medium 、关注我们的 Twitter,并加入 Discord 社区…...

antd setFieldsValue 设置初始值无效AutoComplete 设置默认值失败
antd form setFieldsValue 设置初始值无效 解决方案 setTimeout(()>{setFieldsValue(values)},100)antd AutoComplete 设置默认值失败 defaultValue 设置无效 解决方案 设置value,搭配onChange来设置修改...

01-Redis核心数据结构与高性能原理
上一篇: 1.Redis安装 下载地址:http://redis.io/download 安装步骤: # 安装gcc yum install gcc# 把下载好的redis-5.0.3.tar.gz放在/usr/local文件夹下,并解压 wget http://download.redis.io/releases/redis-5.0.3.tar.gz…...

预防Dos攻击
Dos----拒绝服务攻击,一般是构造特殊的输入,使得后台的处理耗时远超正常水平,随着请求越来越多,后台服务越发疲于奔命,最后因资源耗尽,无法再接受新的请求,最终造成拒绝服务的效果。 特殊输入例…...

ant design的文档真的是一坨屎
很多基础设置 高傲的写都不写 要自己去index.d.ts里查 这就算了,为什么还有错的。。。。。 即使因为版本号而不同,起码把差异说明一下吧,直接丢个错的什么意思,。。。。。。。。 没点子功夫还真用不了 文档 进度条 Progress -…...

关于迁移学习的一点理解
举个栗子,老虎图片的数量非常少,可以让网络先学会识别猫的图片 1、预训练模型 内容:利用在 ImageNet1000 数据集训练好的模型,将所需的模型参数下载,嵌入到对应的网络架构中,使用对预训练模型的搭建。目前P…...
【力扣周赛】第 361 场周赛(⭐前缀和+哈希表 树上倍增、LCA⭐)
文章目录 竞赛链接Q1:7020. 统计对称整数的数目竞赛时代码——枚举预处理 Q2:8040. 生成特殊数字的最少操作(倒序遍历、贪心)竞赛时代码——检查0、00、25、50、75 Q3:2845. 统计趣味子数组的数目竞赛时代码——前缀和…...
解决 Android 依赖冲突
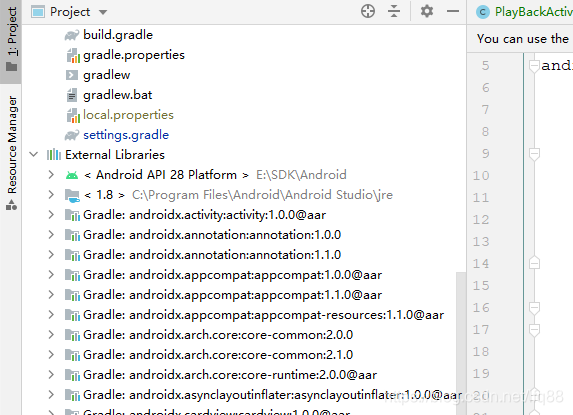
解决办法 问题原因就是,各个模块所有的依赖(递归)的 jar 包最后都会加载到安卓的项目中,你可以选择 project 形式查看 External Libraries,都在这了。所以解决问题关键就是干掉冲突,剩下一个就行了…...
前端设计模式基础笔记
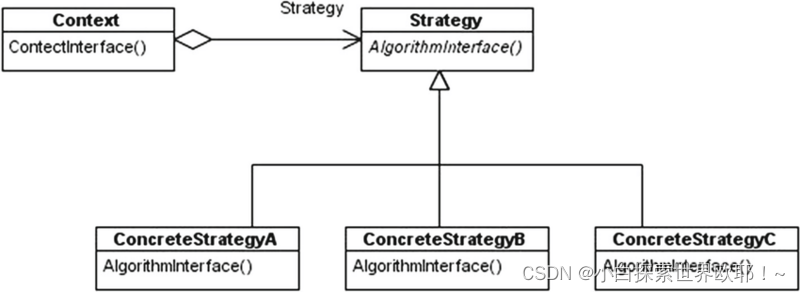
前端设计模式是指在前端开发中经常使用的一些解决问题的模式或思想。它们是经过实践证明的最佳实践,可以帮助我们更好地组织和管理我们的代码。 一、单例模式(Singleton Pattern) 单例模式是一种创建型模式,它保证一个类只有一个…...

Python项目开发:Flask基于Python的天气数据可视化平台
目录 步骤一:数据获取 步骤二:设置Flask应用程序 步骤三:处理用户输入和数据可视化 步骤四:渲染HTML模板 总结 在这个数字化时代,数据可视化已经成为我们理解和解释信息的重要手段。在这个项目中,我们…...

Dell 服务器常见报错信息汇总
Dell 服务器常见报错汇总 如果有别的报错信息欢迎补充...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...
