【1462. 课程表 IV】
来源:力扣(LeetCode)
描述:
你总共需要上 numCourses 门课,课程编号依次为 0 到 numCourses-1 。你会得到一个数组 prerequisite ,其中 prerequisites[i] = [ai, bi] 表示如果你想选 bi 课程,你 必须 先选 ai 课程。
- 有的课会有直接的先修课程,比如如果想上课程
1,你必须先上课程0,那么会以[0,1]数对的形式给出先修课程数对。
先决条件也可以是 间接 的。如果课程 a 是课程 b 的先决条件,课程 b 是课程 c 的先决条件,那么课程 a 就是课程 c 的先决条件。
你也得到一个数组 queries ,其中 queries[j] = [uj, vj]。对于第 j 个查询,您应该回答课程 uj 是否是课程 vj 的先决条件。
返回一个布尔数组 answer ,其中 answer[j] 是第 j 个查询的答案。
示例 1:
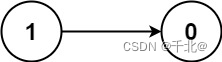
输入:numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
输出:[false,true]
解释:课程 0 不是课程 1 的先修课程,但课程 1 是课程 0 的先修课程。
示例 2:
输入:numCourses = 2, prerequisites = [], queries = [[1,0],[0,1]]
输出:[false,false]
解释:没有先修课程对,所以每门课程之间是独立的。
示例 3:
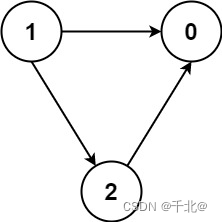
输入:numCourses = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
输出:[true,true]
提示:
- 2 <= numCourses <= 100
- 0 <= prerequisites.length <= (numCourses * (numCourses - 1) / 2)
- prerequisites[i].length == 2
- 0 <= ai, bi <= n - 1
- ai != bi
- 每一对 [ai, bi] 都 不同
- 先修课程图中没有环。
- 1 <= queries.length <= 104
- 0 <= ui, vi <= n - 1
- ui != vi
方法一:广度优先搜索 + 拓扑排序
思路与算法
题目给出 numCourses 门课(编号从 0 开始),并给出了一个长度为 n 的课程之间的制约关系数组 prerequisite ,其中 prerequisite[i] = [ai, bi] 表示在学习课程 bi 之前必须要完成课程 ai 的学习,即课程 ai 为 bi 的先决条件。我们可以将上述条件构建一张有向图——将每一个课程看作一个点(课程编号即为点的编号),每一个制约关系 prerequisite[i] = [ai,bi] 对应一条从点 ai 指向 bi 的有向边,并且题目保证了这样构建出来的图不存在环。
现在有 m 个查询 queries,其中对于第 i 个查询 queries[i] = [ui,vi],我们需要判断课程 ui 是否是课程 vi 的直接或间接先决条件。我们创建一个 numCourses×numCourses 的矩阵 isPre,其中 isPre[x][y] 表示课程 x 是否是课程 y 的直接或间接先决条件,若是则 isPre[x][y] = True,否则 isPre[x][y] = False。在完成 isPre 计算后,我们对于每一个查询就可以在 O(1) 时间得到结果。对于 isPre 的计算,我们可以通过「广度优先搜索」+「拓扑排序」来对矩阵 isPre 进行计算:
首先我们需要计算有向图中每一个节点的入度,并对入度为 0 的节点加入队列。然后只要队列非空,就进行以下操作:
- 取出队列队首元素,同时,将这个节点及其所有前置条件节点设置为所有后续节点的前置条件节点,然后对每一个后续节点入度进行 −1 操作,若操作后的节点入度为 0,则继续将该节点加入队列。
「拓扑排序」结束后,矩阵 isPre 计算完毕,然后我们遍历每一个查询,根据矩阵 isPre 即可得到每一个查询的结果。
代码:
class Solution {
public:vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {vector<vector<int>> g(numCourses);vector<int> indgree(numCourses, 0);vector<vector<bool>> isPre(numCourses, vector<bool>(numCourses, false));for (auto& p : prerequisites) {++indgree[p[1]];g[p[0]].push_back(p[1]);}queue<int> q;for (int i = 0; i < numCourses; ++i) {if (indgree[i] == 0) {q.push(i);}}while (!q.empty()) {auto cur = q.front();q.pop();for (auto& ne : g[cur]) {isPre[cur][ne] = true;for (int i = 0; i < numCourses; ++i) {isPre[i][ne] = isPre[i][ne] | isPre[i][cur];}--indgree[ne];if (indgree[ne] == 0) {q.push(ne);}}}vector<bool> res;for (auto& query : queries) {res.push_back(isPre[query[0]][query[1]]);}return res;}
};
时间 232ms 击败 46.33%使用 C++ 的用户
内存 58.08MB 击败 61.78%使用 C++ 的用户
复杂度分析
- 时间复杂度:O(numCourses2+n+m),其中 numCourses 为课程数,n 为题目给出的先决条件的数目,m 为题目给出的查询数,其中通过计算矩阵 isPre 的时间复杂度为 O(numCourses2),构建有向图的复杂度为 O(numCourses+n),处理每一个查询的复杂度为 O(1),共有 m 个查询,所以总的查询时间复杂度为 O(m)。
- 空间复杂度:O(numCourses2+n),其中 numCourses 为课程数,n 为题目给出的先决条件的数目,主要为构建有向图和矩阵 isPre 的空间开销。注意返回值不计入空间复杂度。
方法二:深度优先搜索 + 拓扑排序
思路与算法
「方法一」中「拓扑排序」的实现同样可以通过「深度优先搜索」来实现。与「广度优先搜索」计入每一个点的出度不同,通过「深度优先搜索」需要记录每一个点是否被访问,我们用 vi[x] 来表示课程 x 是否被访问,初始时为 False。
我们从编号小到大遍历全部节点,若节点 i 未被访问,则进入「深度优先搜索」流程:
- 若当前节点 x 已被访问,则直接返回。
- 若当前节点 x 未被访问,将访问状态设为已访问,然后继续对其全部后继节点递归进行「深度优先搜索」流程。将节点 x 置为其每一个后继节点 y 的先决条件,有 isPre[x][y] = True,以及对于每一个以 y 为先决条件的节点 t,节点 x 同样为 t 的先决条件,有 isPre[x][t] = True。
遍历完成后,「拓扑排序」完成,矩阵 isPre 计算完毕,然后我们遍历每一个查询,根据矩阵 isPre 即可得到每一个查询的结果。
代码:
class Solution {
public:void dfs(vector<vector<int>>& g, vector<vector<bool>>& isPre, vector<bool>& vi, int cur) {if (vi[cur]) {return;}vi[cur] = true;for (auto& ne : g[cur]) {dfs(g, isPre, vi, ne);isPre[cur][ne] = true;for (int i = 0; i < isPre.size(); ++i) {isPre[cur][i] = isPre[cur][i] | isPre[ne][i];}}}vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {vector<vector<int>> g(numCourses);vector<bool> vi(numCourses, false);vector<vector<bool>> isPre(numCourses, vector<bool>(numCourses, false));for (auto& p : prerequisites) {g[p[0]].push_back(p[1]);}for (int i = 0; i < numCourses; ++i) {dfs(g, isPre, vi, i);}vector<bool> res;for (auto& query : queries) {res.push_back(isPre[query[0]][query[1]]);}return res;}
};
时间 212ms 击败 55.98%使用 C++ 的用户
内存 57.84MB 击败 73.75%使用 C++ 的用户
复杂度分析
- 时间复杂度:O(numCourses2+n+m) ,其中 numCourses 为课程数,n 为题目给出的先决条件的数目,m 为题目给出的查询数,其中计算矩阵 isPre 的时间复杂度为 O(numCourses2) ,构建有向图的复杂度为 O(numCourses+n),处理每一个查询的复杂度为 O(1),共有 m 个查询,所以总的查询时间复杂度为 O(m)。
- 空间复杂度:O(numCourses2+n) ,其中 numCourses 为课程数,n 为题目给出的先决条件的数目,主要为构建有向图和矩阵 isPre 的空间开销。注意返回值不计入空间复杂度。
author:力扣官方题解
相关文章:

【1462. 课程表 IV】
来源:力扣(LeetCode) 描述: 你总共需要上 numCourses 门课,课程编号依次为 0 到 numCourses-1 。你会得到一个数组 prerequisite ,其中 prerequisites[i] [ai, bi] 表示如果你想选 bi 课程,你…...

Kerberos 身份验证
简介 Kerberos 是一种由 MIT(麻省理工大学)提出的一种基于加密 Ticket 的身份认证协议。它旨在通过使用密钥加密技术为客户端/服务器应用程序提供强身份验证,用于验证用户或主机的标识。。 适用范围:Windows Server 2022、Window…...

R语言贝叶斯METROPOLIS-HASTINGS GIBBS 吉布斯采样器估计变点指数分布分析泊松过程车站等待时间...
原文链接:http://tecdat.cn/?p26578 指数分布是泊松过程中事件之间时间的概率分布,因此它用于预测到下一个事件的等待时间,例如,您需要在公共汽车站等待的时间,直到下一班车到了(点击文末“阅读原文”获取…...

通付盾入选2023年度“上市苗圃工程”重点企业
近日,2023年度苏州工业园区企业上市苗圃工程认定名单公示,江苏通付盾科技有限公司成功入选园区“上市苗圃工程”重点企业。 2023年第一批次苗圃企业认定结果: 企业上市苗圃工程 上市企业是衡量地方综合经济实力的重要标尺,也是区…...

SpringMVC之文件上传下载
SpringMVC是一个基于Java的Web框架,它提供了一套用于构建Web应用程序的开发模型。在SpringMVC中,文件上传和下载是常见的功能之一。 SpringMVC文件上传和下载的介绍: 介绍文件上传: 在SpringMVC中,文件上传功能可以通…...
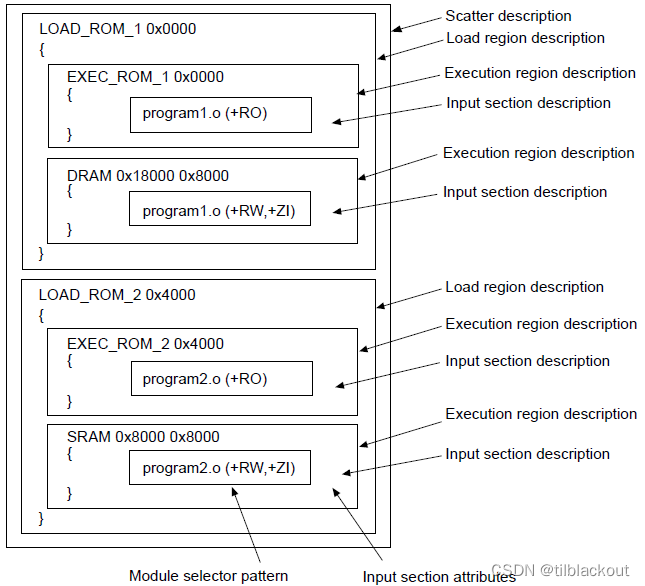
嵌入式IDE(2):KEIL中SCF分散加载链接文件详解和实例分析
在上一篇文章IAR中ICF链接文件详解和实例分析中,我通过I.MX RT1170的SDK中的内存映射关系,分析了IAR中的ICF链接文件的语法。对于MCU编程所使用的IDE来说,IAR和Keil用得比较多,所以这一篇文章就来分析一下Keil的分散文件.scf(scat…...

Linux防火墙常用操作及端口开放
Linux防火墙常用操作及端口开放 1.查看防火墙状态 firewall-cmd --state 2.开启防火墙 systemctl start firewalld.service 3.开启指定端口 firewall-cmd --zonepublic --add-port3306/tcp --permanent firewall-cmd --zonepublic --add-port6379/tcp --permanent 显示success表…...

[JAVAee]Linux上的javax.mail报错
我们把在window写的项目部署到Linux上的Tomcat时,如果发现使用不了了,该如何找到错误呢?找到报错的地方在哪呢? 在Linux环境下来到Tomcat目录下的logs目录,输入: tail -f catalina.out -n 500 tail 就是把文件的末尾几行读取到终端上,并会持续刷新 -f 循环读取 catalina.ou…...

开学季|校园迎新哪家强?VR全景来导航
九月开学迎新季,各大高校的迎新活动开展的如火如荼,随着科技的不断进步,高校为了更好的开展迎新活动,让新生们尽快熟悉新的校园和生活,会利用VR全景技术带领着新生进行校园游览,给予新生们巨大便利的同时&a…...
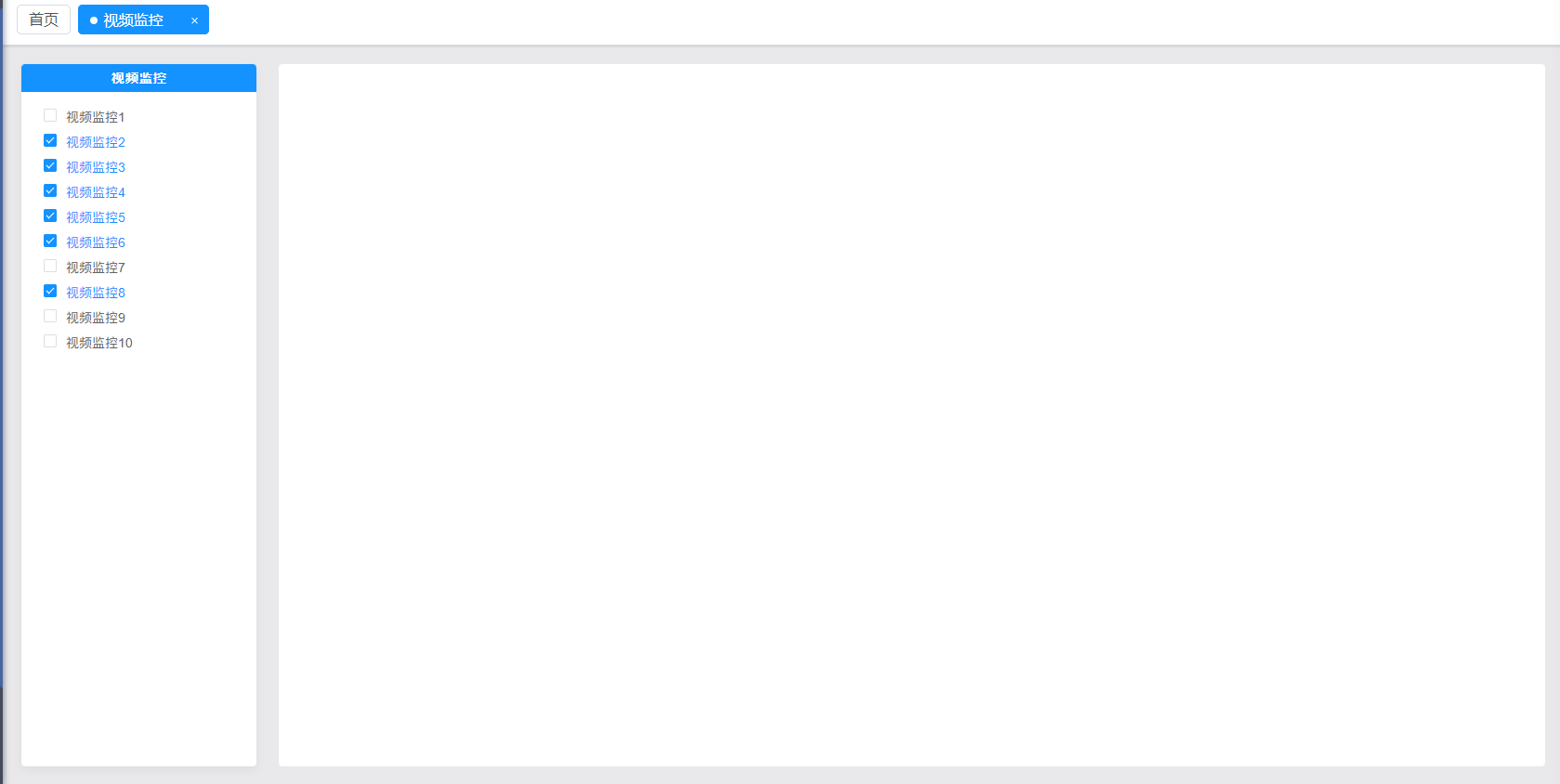
el-checkbox-group限制勾选数量
<!--* Description: 视频监控 页面* Author: mhf* Date: 2023-08-15 13:26:33 --> <template><div class"videoSurveillance"><el-row :gutter"24"><el-col :span"4"><div class"videoSurveillance-left&…...

【JavaScript】WebAPI入门到实战
文章目录 一、WebAPI背景知识1. 什么是WebAPI?2. 什么是API? 二、DOM基本概念三、获取元素三、事件初识1. 点击事件2. 键盘事件 四、操作元素1. 获取/修改元素内容2. 获取/修改元素属性3. 获取/修改表单元素属性4. 获取/修改样式属性 五、操作节点1. 新增…...

奥康的高尔夫鞋,圈不住投资者的心
文 | 螳螂观察 作者 | 青月 鞋服行业终于熬过了“寒冬”,2023年行业景气度开始逐步回暖。 东方财富Choice数据显示,截至8月17日,已有28家鞋帽服装类上市公司发布了2023年中期业绩预告或快报,其中,9家预增࿰…...
vue2配置环境变量并且nginx运行成功
需求:我在vue项目配置了生产环境和开发环境,之后通过proxy代理的方式把地址转发到真实的服务器地址上用于请求接口,之后把项目打包后上传到nginx上,之后接口报错404,但是本地运行是可以访问的,找了很久终于…...

Java+Swing形成GUI图像界面
一、Swing 简介 Swing 主要用来开发 GUI 程序,GUI(Graphical User Interface)即图形用户界面。Java 中针对 GUI 设计提供了丰富的类库,这些类分别位于 java.awt 和 java.swing 中,简称 AWT 和 Swing ;其中,AWT(Abstract Window Toolkit)是抽象窗口工具包,是 Java 平…...

编辑距离 -- 动规
72. 编辑距离 给出动规的两种常见实现形式:自顶向下、自底向上,前者一般借助递归函数备忘录实现,后者通常基于dp数组实现。 class MinDistance:"""72. 编辑距离https://leetcode.cn/problems/edit-distance/""&quo…...

douyin【商品抢购js脚本】
文章目录 前言订阅须知知识点源码前言 脚本主要用来实现抢购douyin商城、直播间秒杀商品等一系列商品 订阅须知 订阅后,只提供js源代码,不提供教学,请根据源码自行抓包知识点 1、在查询串插入一个固定的键rstr 2、对查询串进行按键排序并取值,对空格和+进行转义为a …...
常见Web安全技术总结!474页Web安全从入门到精通(附PDF)
Web安全范围比较大,知识点比较杂,很多朋友都无从下手,这不可怕,可怕的是乱下手,其实往往基础才是决定你是否能走远的关键。 为了帮助大家入门网安,给大家推荐一份《新手Web安全入门到精通》,共…...

Prometheus 监控指南:如何可靠地记录数字时间序列数据
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🐅🐾猫头虎建议程序员必备技术栈一览表📖: 🛠️ 全栈技术 Full Stack: 📚…...
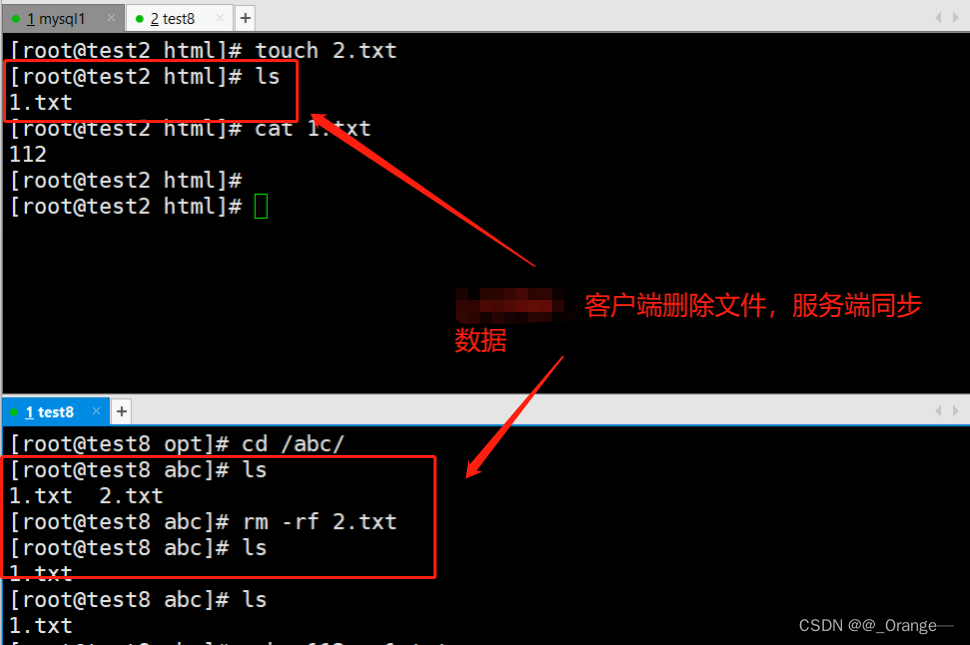
rsync远程同步+inotify监控
目录 一、Rsync 简介 1、rsync是什么 2、备份的方式 3、rsync同步方式 4、常用rsync命令 5、配置源的两种表达方法 二、rsync实验 1、本地复制 编辑编辑 2、异地复制 2.1 rsync服务器配置 2.2 rsync客户端配置 2.2.1 普通同步 2.2.2 免密同步 2.2.3 --delet…...

【面试经典150 | 数组】移除元素
文章目录 写在前面Tag题目来源题目解读解题思路方法一:原地操作 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...
