【深度学习】Mini-Batch梯度下降法
Mini-Batch梯度下降法
在开始Mini-Batch算法开始之前,请确保你已经掌握梯度下降的最优化算法。
在训练神经网络时,使用向量化是加速训练速度的一个重要手段,它可以避免使用显式的for循环,并且调用经过大量优化的矩阵计算函数库。但是当数量增加到一定级别的时候,比如说五百万、五千万或者更大,此时此刻即便是进行了向量化,其训练速度也是挺慢的。Mini-Batch最优化算法则可以加速这种情况下的训练过程。
字如其名,Mini-Batch梯度下降法就是将数据集划分为若干个更小的数据集(Mini-Batch),然后依次对小规模数据集进行处理。假设每一个子集中只有1000个数据样本,那么在总样本量为500万的时候,会被分为5000个子集。原数据集的特征部分为 x ( 1 ) , x ( 2 ) , x ( 3 ) . . . x ( 1000 ) , x ( 1001 ) . . . . x ( m ) x^{(1)},x^{(2)},x^{(3)}...x^{(1000)},x^{(1001)}....x^{(m)} x(1),x(2),x(3)...x(1000),x(1001)....x(m),现在被划分为:
X { 1 } = x ( 1 ) , x ( 2 ) , x ( 3 ) . . . x ( 1000 ) X { 2 } = x ( 1001 ) , x ( 1002 ) , x ( 1003 ) . . . x ( 2000 ) X { 3 } = x ( 2001 ) , x ( 2002 ) , x ( 2003 ) . . . x ( 3000 ) X^{\{1\}}=x^{(1)},x^{(2)},x^{(3)}...x^{(1000)}\\ X^{\{2\}}=x^{(1001)},x^{(1002)},x^{(1003)}...x^{(2000)}\\ X^{\{3\}}=x^{(2001)},x^{(2002)},x^{(2003)}...x^{(3000)} X{1}=x(1),x(2),x(3)...x(1000)X{2}=x(1001),x(1002),x(1003)...x(2000)X{3}=x(2001),x(2002),x(2003)...x(3000)
其中 X { i } X^{\{i}\} X{i}表示第i个Mini-Batch的样本集
同样地,标签集也被划为5000个子集,分别是
Y { 1 } = y ( 1 ) , y ( 2 ) , y ( 3 ) . . . y ( 1000 ) Y { 2 } = y ( 1001 ) , y ( 1002 ) , y ( 1003 ) . . . y ( 2000 ) Y { 3 } = y ( 2001 ) , y ( 2002 ) , x ( 2003 ) . . . x ( 3000 ) Y^{\{1\}}=y^{(1)},y^{(2)},y^{(3)}...y^{(1000)}\\ Y^{\{2\}}=y^{(1001)},y^{(1002)},y^{(1003)}...y^{(2000)}\\ Y^{\{3\}}=y^{(2001)},y^{(2002)},x^{(2003)}...x^{(3000)} Y{1}=y(1),y(2),y(3)...y(1000)Y{2}=y(1001),y(1002),y(1003)...y(2000)Y{3}=y(2001),y(2002),x(2003)...x(3000)
其中 Y { i } Y^{\{i}\} Y{i}表示第i个Mini-Batch的标签集
一个完整的Mini-Batch子集由标签子集和样本子集构成,第i个Mini-Batch子集等于 ( X { i } , Y { i } ) (X^{\{i\}},Y^{\{i\}}) (X{i},Y{i})
接下来说一下向量化表示,假设一个样本有n个特征,一个Mini-Batch有m个样本,那么他的KaTeX parse error: Expected 'EOF', got '}' at position 2: X}̲应该是一个m行n列的矩阵,他的Y是一个m行1列的矩阵
划分完自己之后,然后我们会单独处理各个Mini-Batch子集。比如说先前向传播,然后计算代价函数,根据代价函数反向传播求出梯度下降中的导数,然后使用梯度下降进行计算。就和一个神经网络差不多,不是吗?总的来说就是训练规模较大的神经网络的时候,我们应该将他们切分为若干个较小的子集,然后让各个子集独立地进行神经网路的训练,就是这样。
在传统的梯度下降中(左图),代价函数cost应该随着迭代的进行而逐渐下降;但是在Mini-Batch中就不一样了,他的cost函数会有一定的波动,但是整体应该是向下的(右图)
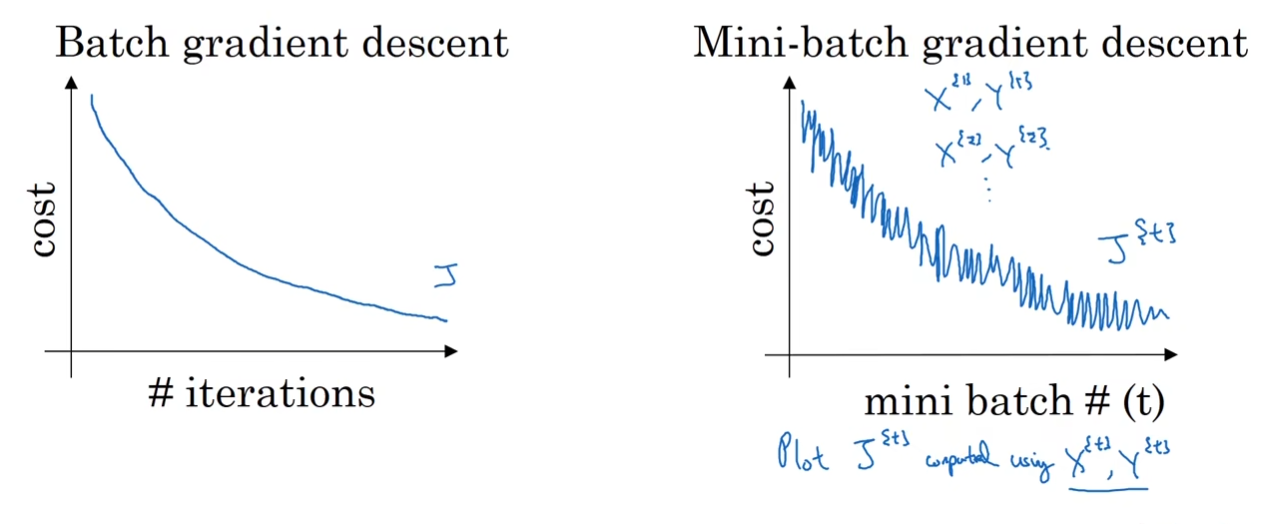
此外,需要我们个人决定的一个关键参数是Mini-Batch的大小,假设如果将一个数据集只划分为1个Mini-Batch,那么实际上他就是普通的梯度下降法,这是情况1;另一个极端是,一个Mini-Batch中只有一个样本,每个样本就是一个Mini-Batch,这种情况下的算法称之为随机梯度下降,这是情况2。
在情况1中,其实就是普通的梯度下降,他下降会十分“顺滑”,这是因为相对噪音比较小,但是对样本量大的情况来说,他将会相当耗时(蓝线)。而在情况2中,因为每个样本都是单独的Mini-Batch,大多数时候会朝着最小值前进,但是有一些样本是噪声样本,因此偶尔会指向错误的方向,因此这会使得其路线十分的九转十八弯(紫线)。而且他不会稳定收敛于一个点,而是在最小值的周围反复打转
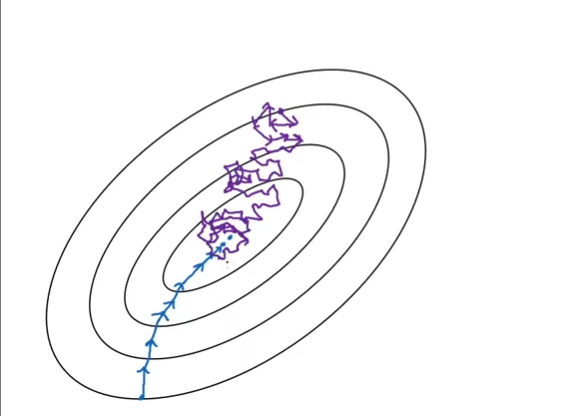
上述的两个极端例子我们可以知道,当Mini-Batch子集设计的太大的时候,虽然噪声少,下降较为顺滑,但是会有较大的时间开销;反之,较小的子集会导致噪声较大,下降的精度不高,但是单次训练速度快,而且较小的子集也无法充分来自于向量化的训练加速,总训练时间反而不是最快的。在实际中,选择适中的子集大小能够保证一定的精度,也能提高速度,并且利用好向量化带来的加速,在此基础之上,根据自己的目标选择合适的子集大小,平衡好训练速度和精度问题
相关文章:

【深度学习】Mini-Batch梯度下降法
Mini-Batch梯度下降法 在开始Mini-Batch算法开始之前,请确保你已经掌握梯度下降的最优化算法。 在训练神经网络时,使用向量化是加速训练速度的一个重要手段,它可以避免使用显式的for循环,并且调用经过大量优化的矩阵计算函数库。…...

AI项目六:WEB端部署YOLOv5
若该文为原创文章,转载请注明原文出处。 一、介绍 最近接触网页大屏,所以就想把YOLOV5部署到WEB端,通过了解,知道了两个方法: 1、基于Flask部署YOLOv5目标检测模型。 2、基于Streamlit部署YOLOv5目标检测。 代码在…...

敲代码常用快捷键
1、代码拖动 PyCharm:按住 shiftalt鼠标选中某一区域来拖动,即可实现拖动这一区域至指定区域。Visual Studio Code (VSCode): - Windows/Linux:Alt 鼠标左键拖动 - MacOS:Option 鼠标左键拖动 IntelliJ IDEA: - Win…...

MyBatis: 分页插件PageHelper直接传递分页参数的用法
一、加分页插件依赖 <dependency><groupId>com.github.pagehelper</groupId><artifactId>pagehelper-spring-boot-starter</artifactId><version>1.2.13</version></dependency>二、配置分页插件,并配置相关属性&a…...
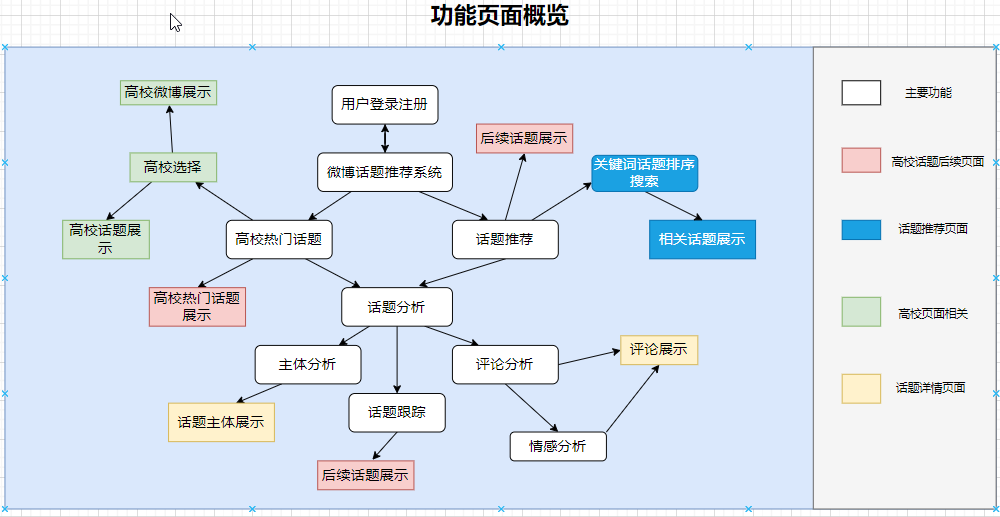
Python基于Flask的高校舆情分析,舆情监控可视化系统
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W,Csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 运行效果图 基于Python的微博大数据舆情分析,舆论情感分析可视化系统 系统介绍 微博舆情分析系…...

Python第一次作业练习
题目分析: """ 参考学校的相关规定。 对于四分制,百分制中的90分及以上可视为绩点中的4分,80 分及以上为3分,70 分以上为2分,60 分以上为1分; 五分制中的5分为四分制中的4分,4分为3分&#…...

InstallShield打包升级时不覆盖原有文件的解决方案
一个.NET Framework的Devexpress UI Windows Form项目,用的InstallShield,前些个版本都好好的,最近几个版本突然就没法更新了,每次更新的时候都覆盖不了原文件,而且这样更新后第一次打开程序(虽然是老程序&…...

服务器巡检表-监控指标
1、巡检指标 系统资源K8S集群NginxJAVA应用RabbitMQRedisPostgreSQLElasticsearchELK日志系统 2、巡检项 检查项目 检查指标 检查标准 系统资源 CPU 使用率 正常:<70% 低风险:≥ 70% 中风险:≥ 85% 高风险:≥ 9…...

无涯教程-JavaScript - DDB函数
描述 DDB函数使用双倍余额递减法或您指定的某些其他方法返回指定期间内资产的折旧。 语法 DDB (cost, salvage, life, period, [factor])争论 Argument描述Required/OptionalCostThe initial cost of the asset.RequiredSalvage 折旧结束时的价值(有时称为资产的残值)。 该…...
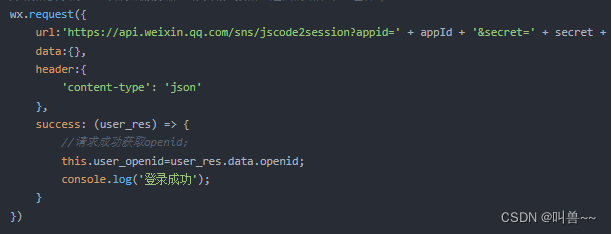
uniapp打包微信小程序。报错:https://api.weixin.qq.com 不在以下 request 合法域名列表
场景:在进行打包上传测试时,发现登录失效,但在测试中【勾选不效应合法域名】就可以。 出现原因:我在获取到用户code后,直接使用调用官方接口换取openid 解决方案: 可以把code带给后端,让他们返…...
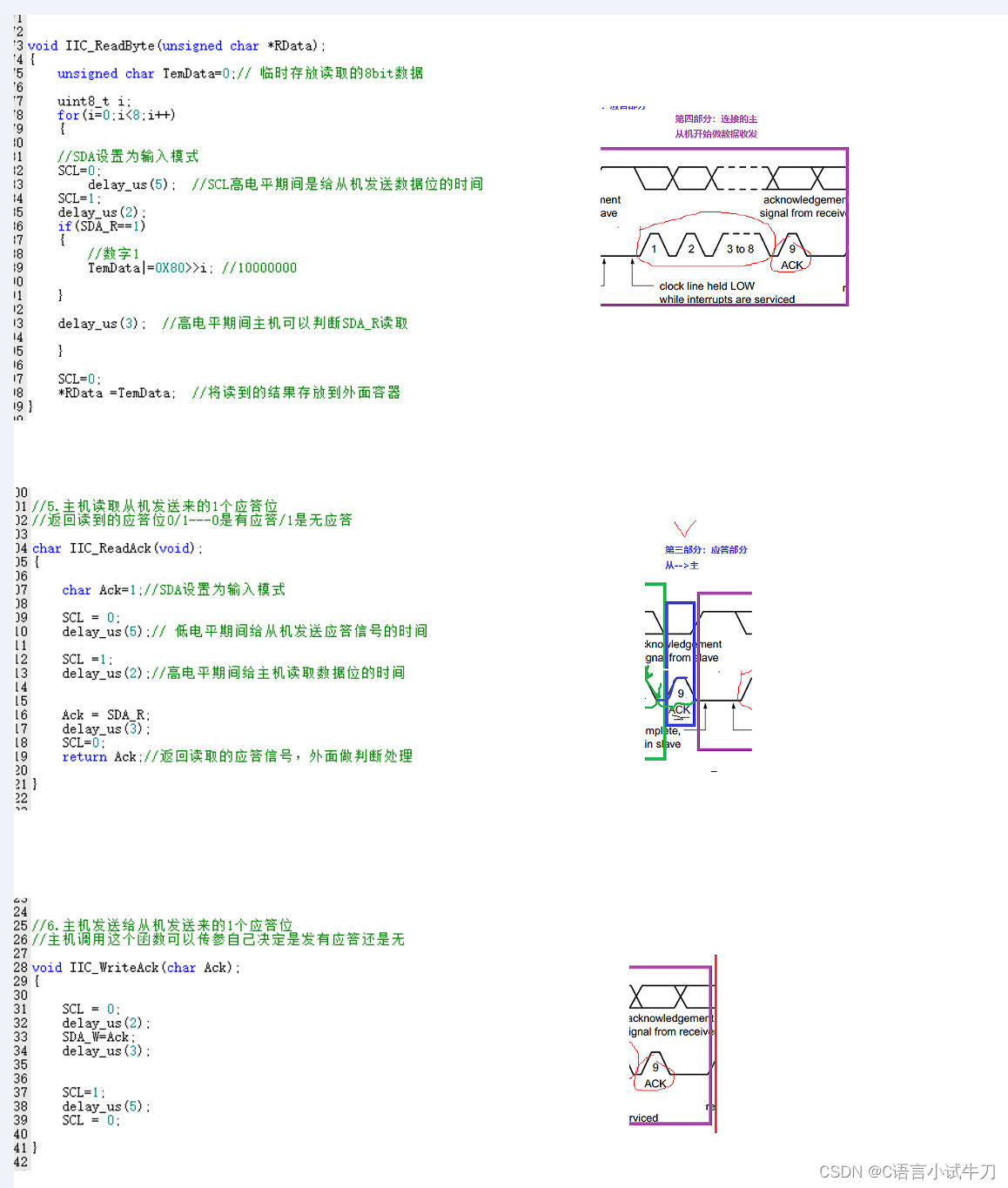
stm32之31.iic
iic双线制。一根是SCL,作为时钟同步线;一根是SDA,作为数据传输线 SDN #include "iic.h"#define SCL PBout(8)#define SDA_W PBout(9) #define SDA_R PBin(9)void IIC_GPIOInit(void) {GPIO_InitTypeDef GPIO_InitStructure;//使能时钟GR…...

新的 ChatGPT 提示工程技术:程序模拟
即时工程的世界在各个层面上都令人着迷,并且不乏巧妙的方法来推动像 ChatGPT 这样的代理生成特定类型的响应。思想链 (CoT)、基于指令、N-shot、Few-shot 等技术,甚至奉承/角色分配等技巧都是充满提示的库背后的灵感,旨在满足各种需求。 在本文中,我将深入研究一项技术,据…...
【Python】爬虫基础
爬虫是一种模拟浏览器实现,用以抓取网站信息的程序或者脚本。常见的爬虫有三大类: 通用式爬虫:通用式爬虫用以爬取一整个网页的信息。 聚焦式爬虫:聚焦式爬虫可以在通用式爬虫爬取到的一整个网页的信息基础上只选取一部分所需的…...
(三、优先队列用于归并排序))
leetcode分类刷题:队列(Queue)(三、优先队列用于归并排序)
1、当TopK问题出现在多个有序序列中时,就要用到归并排序的思想了 2、将优先队列初始化为添加多个有序序列的首元素的形式,再循环K次优先队列的出队和出队元素对应序列下个元素的入队,就能得到TopK的元素了 3、这些题目好像没有TopK 大用小顶堆…...

无线窨井水位监测仪|排水管网智慧窨井液位计安装案例
城市窨井在城市排水、雨水、污水输送等方面发挥着重要作用,是污水管网、排水管网 建设重要的组成部分。随着城镇精细化建设及人民安全防范措施水平的提高,对窨井内水位的监测提出了更高的要求,他是排水管网问题的晴雨表,窨井信息化…...

024 - STM32学习笔记 - 液晶屏控制(一) - LTDC与DMA2D初始
024- STM32学习笔记 - LTDC控制液晶屏 在学习如何控制液晶屏之前,先了解一下显示屏的分类,按照目前市场上存在的各种屏幕材质,主要分为CRT阴极射线管显示屏、LCD液晶显示屏、LED显示屏、OLED显示屏,在F429的开发板上,…...
)
Python数据容器:dict(字典、映射)
1、什么是字典 Python中的字典是通过key找到对应的Value(相当于现实生活中通过“字”找到“该字的含义” 我们前面所学习过的列表、元组、字符串以及集合都不能够提供通过某个东西找到其关联的东西的相关功能,字典可以。 例如 这里有一份成绩单…...
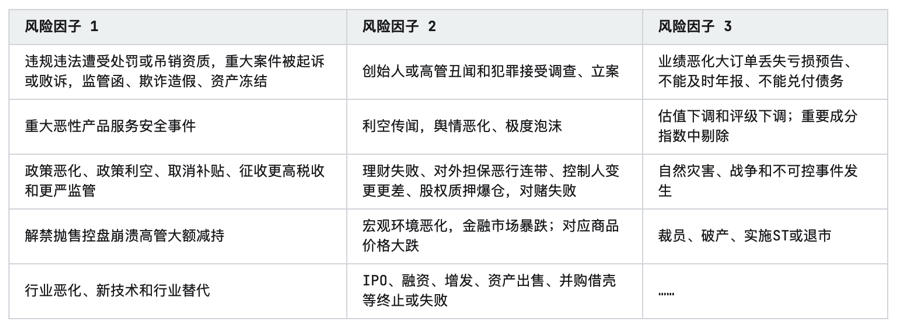
2023年基因编辑行业研究报告
第一章 行业发展概况 1.1 定义 基因编辑(Gene Editing),又称基因组编辑(Genome Editing)或基因组工程(Genome Engineering),是一项精确的科学技术,可以对含有遗传信息的…...
Spring MVC:请求转发与请求重定向
Spring MVC 请求转发请求重定向附 请求转发 转发( forward ),指服务器接收请求后,从一个资源跳转到另一个资源中。请求转发是一次请求,不会改变浏览器的请求地址。 简单示例: 1.通过 String 类型的返回值…...

按键灯待机2秒后灭掉
修改文件:/device/mediatek/mt6580/init.mt6580.rc chown system system /sys/class/leds/red/triggerchown system system /sys/class/leds/green/triggerchown system system /sys/class/leds/blue/triggerchown system system sys/devices/platform/device_info/…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...
