LeetCode377. 组合总和 Ⅳ
377. 组合总和 Ⅳ
文章目录
- [377. 组合总和 Ⅳ](https://leetcode.cn/problems/combination-sum-iv/)
- 一、题目
- 二、题解
- 方法一:完全背包一维数组
- 动态规划思路
- 代码分析
- 方法二:动态规划二维数组
一、题目
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。
示例 1:
输入:nums = [1,2,3], target = 4
输出:7
解释:
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意,顺序不同的序列被视作不同的组合。
示例 2:
输入:nums = [9], target = 3
输出:0
提示:
1 <= nums.length <= 2001 <= nums[i] <= 1000nums中的所有元素 互不相同1 <= target <= 1000
进阶:如果给定的数组中含有负数会发生什么?问题会产生何种变化?如果允许负数出现,需要向题目中添加哪些限制条件?
二、题解
这道题要求我们找出由给定数组 nums 中的不同元素组成的总和等于 target 的组合个数,说是组合,其实实质上是排列,我在这篇文章里讲述了关于排列组合的区别并且手写了动态规划过程:https://blog.csdn.net/m0_61843614/article/details/132745696。
方法一:完全背包一维数组
动态规划思路
定义一个一维数组 dp,其中 dp[i] 表示总和为 i 的组合个数。
我们的目标是计算 dp[target],也就是总和为 target 的组合个数。为了计算 dp[target],可以考虑如下的思路:
-
初始化一个长度为
target + 1的数组dp,并将其所有元素初始化为0。dp[i]表示总和为i的组合个数。 -
由于组合的元素可以重复使用,我们可以遍历数组
nums中的每个元素,并尝试将其加入到总和为i的组合中。 -
对于每个元素
nums[j],我们可以检查dp[i - nums[j]],它表示总和为i - nums[j]的组合个数。我们可以将dp[i - nums[j]]加到dp[i]上,表示将nums[j]加入到当前组合中。 -
重复上述步骤,直到遍历完数组
nums中的所有元素。 -
最终,
dp[target]就是我们要求的答案,表示总和为target的组合个数。
代码分析
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<long long> dp(target + 1, 0);dp[0] = 1; // 初始化,总和为0的组合个数为1for (int i = 0; i <= target; i++) {for (int j = 0; j < nums.size(); j++) {if (nums[j] <= i && dp[i] < INT_MAX - dp[i - nums[j]]) {dp[i] = dp[i] + dp[i - nums[j]]; // 更新 dp[i]}}}return dp[target];}
};
现在我逐步解释代码的各个部分:
-
我们定义了一个一维数组
dp,长度为target + 1,并将所有元素初始化为0。 -
初始化
dp[0]为1,因为总和为0的组合只有一种方式,就是什么都不选。 -
使用两个嵌套的循环,外层循环遍历所有可能的总和
i,内层循环遍历数组nums中的所有元素。 -
在内层循环中,我们检查当前元素
nums[j]是否小于等于i,如果是,就说明可以将nums[j]加入到总和为i的组合中。 -
如果
dp[i]的值还没有越界(小于INT_MAX - dp[i - nums[j]]),则将dp[i - nums[j]]的值加到dp[i]上,表示将nums[j]加入到当前组合中。 -
最终,返回
dp[target],即总和为target的组合个数。
方法二:动态规划二维数组
先给出代码:
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {//dp[j][i]意义是背包容量为i的情况下,最后一个加入的数字是从nums[0]到nums[i]之间的方法的总数vector<vector<long long>> dp(nums.size(), vector<long long>(target + 1, 0));dp[0][0] = 1;for (int i = 0; i <= target; i++) {for (int j = 0; j < nums.size(); j++) {if (j > 0) {dp[j][i] = dp[j - 1][i];}if (i >= nums[j] && dp[j][i] < INT_MAX - dp[nums.size() - 1][i - nums[j]]) {dp[j][i] += dp[nums.size() - 1][i - nums[j]];}}}return dp[nums.size() - 1][target];}
};
- 动态规划思路
这个问题的目标是找出总和为 target 的元素组合的个数。首先,让我们定义一个二维数组 dp,其中 dp[j][i]意义是背包容量为i的情况下,最后一个加入的数字是从nums[0]到nums[i]之间的方法的总数。我们的目标是求 dp[nums.size() - 1][target],即使用所有的元素构成和为 target 的排列的个数。
- 初始化
首先,我们初始化 dp 数组,将所有元素都初始化为 0。然后我们设置 dp[0][0] = 1,这是因为在前 0 个元素中,构成和为 0 的组合有一种方式,即不选择任何元素。
- 填充动态规划数组
接下来,我们使用两个嵌套循环来填充 dp 数组。外层循环 i 表示考虑前 i 个元素,内层循环 j 表示目标和为 j。
-
如果
j < nums[i],意味着当前的元素nums[i]太大,不能加入组合中,所以我们将dp[i][j]设置为dp[i-1][j],表示不选择当前元素时的组合数,继承上一行的值。 -
如果
j >= nums[i],意味着当前的元素nums[i]可以加入组合中。我们需要考虑两种情况:- 不选择当前元素,即
dp[i][j] = dp[i-1][j]。 - 选择当前元素,即
dp[i][j] += dp[i][j - nums[i]],这里的dp[i][j - nums[i]]表示在考虑前i个元素,和为j - nums[i]的组合数。
- 不选择当前元素,即
最终,dp[nums.size() - 1][target] 就代表了使用所有元素构成和为 target 的组合的个数。
- 返回结果
最后,我们返回 dp[nums.size() - 1][target] 即可得到答案。
相关文章:

LeetCode377. 组合总和 Ⅳ
377. 组合总和 Ⅳ 文章目录 [377. 组合总和 Ⅳ](https://leetcode.cn/problems/combination-sum-iv/)一、题目二、题解方法一:完全背包一维数组动态规划思路代码分析 方法二:动态规划二维数组 一、题目 给你一个由 不同 整数组成的数组 nums ࿰…...

QT将数据写入文件,日志记录
项目场景: 在QT应用中,有时候需要将错误信息记录在log文件里面,或者需要将数据输出到文件中进行比对查看使用。 创建log文件,如果文件存在则不创建 QDir dir(QCoreApplication::applicationDirPath()"/recv_data");if(…...

vue2与vue3的使用区别与组件通信
1. 脚手架创建项目的区别: vue2: vue init webpack “项目名称”vue3: vue create “项目名称” 或者vue3一般与vite结合使用: npm create vitelatest yarn create vite2. template中结构 vue2: template下只有一个元素节点 <template><div><div…...

亚信科技与中国信通院达成全方位、跨领域战略合作
9月11日,亚信科技(中国)有限公司「简称:亚信科技」与中国信息通信研究院「简称:中国信通院」在京达成战略合作,双方将在关键技术研发、产业链协同等方面展开全方位、跨领域、跨行业深度合作,共促…...

华为Linux系统开发工程师面试
在Linux系统开发工程师的面试中,你可能会遇到以下一些问题: 在同一个网站中,当客户访问的时候,会出现有的页面访问的速度快而有的慢,系统和服务完全正常、网络带宽正常,你如何诊断这个问题?你以…...

Qt利用QTime实现sleep效果分时调用串口下发报文解决串口下发给下位机后产生的粘包问题
Qt利用QTime实现sleep效果分时调用串口下发报文解决串口下发给下位机后产生的粘包问题 文章目录 Qt利用QTime实现sleep效果分时调用串口下发报文解决串口下发给下位机后产生的粘包问题现象解决方法 现象 当有多包数据需要连续下发给下位机时,比如下载数据等&#x…...
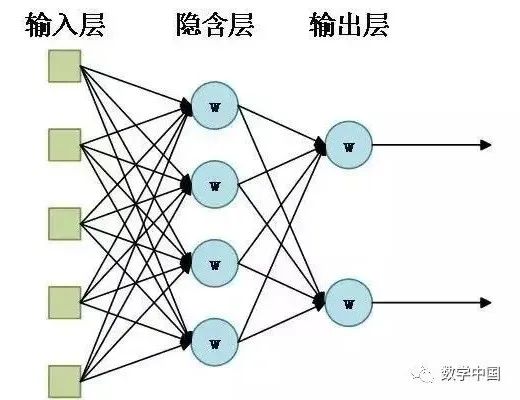
人工智能:神经细胞模型到神经网络模型
人工智能领域中的重要流派之一是:从神经细胞模型(Neural Cell Model)到神经网络模型(Neural Network Model)。 一、神经细胞模型 第一个人工神经细胞模型是“MP”模型,它是由麦卡洛克、匹茨合作࿰…...

Redisson分布式锁实战
实战来源 此问题基于电商 这周遇见这么一个问题,简略的说一下 由MQ发布了两个消息,一个是订单新增,一个是订单状态变更 由于直接付款之后,这两个消息的发布时间不分先后,可能会造成两种情况,1、订单状态变更…...

JavaScript中循环遍历数组、跳出循环和继续循环
循环遍历数组 上个文章我们简单的介绍for循环,接下来,我们使用for循环去读取数据的数据,之前我们写过这样的一个数组,如下: const ITshareArray ["张三","二愣子","2033-1997","…...

Java——》Synchronized和Lock区别
推荐链接: 总结——》【Java】 总结——》【Mysql】 总结——》【Redis】 总结——》【Kafka】 总结——》【Spring】 总结——》【SpringBoot】 总结——》【MyBatis、MyBatis-Plus】 总结——》【Linux】 总结——》【MongoD…...

JDK20 + SpringBoot 3.1.0 + JdbcTemplate 使用
JDK20 SpringBoot 3.1.0 JdbcTemplate 使用 一.测试数据库 Postgres二.SpringBoot项目1.Pom 依赖2.配置文件3.启动类4.数据源配置类5.实体对象类包装类6.测试用实体对象1.基类2.扩展类 7.测试类 通过 JdbcTemplate 直接执行 SQL 语句,结合源码动态编译即可方便实现…...
CTFhub_SSRF靶场教程
CTFhub SSRF 题目 1. Bypass 1.1 URL Bypass 请求的URL中必须包含http://notfound.ctfhub.com,来尝试利用URL的一些特殊地方绕过这个限制吧 1.利用?绕过限制urlhttps://www.baidu.com?www.xxxx.me 2.利用绕过限制urlhttps://www.baidu.comwww.xxxx.me 3.利用斜…...

【华为OD机试】单词接龙【2023 B卷|100分】
【华为OD机试】-真题 !!点这里!! 【华为OD机试】真题考点分类 !!点这里 !! 题目描述: 单词接龙的规则是:可用于接龙的单词首字母必须要前一个单词的尾字母相同; 当存在多个首字母相同的单词时,取长度最长的单词,如果长度也相等, 则取字典序最小的单词;已经参与接龙…...

如何优雅的实现无侵入性参数校验之spring-boot-starter-validation
在开发过程中,参数校验是一个非常重要的环节。但是,传统的参数校验方法往往需要在代码中手动添加大量的 if-else 语句,这不仅繁琐,而且容易出错。为了解决这个问题,我们可以使用无侵入性参数校验的方式来简化代码并提高…...
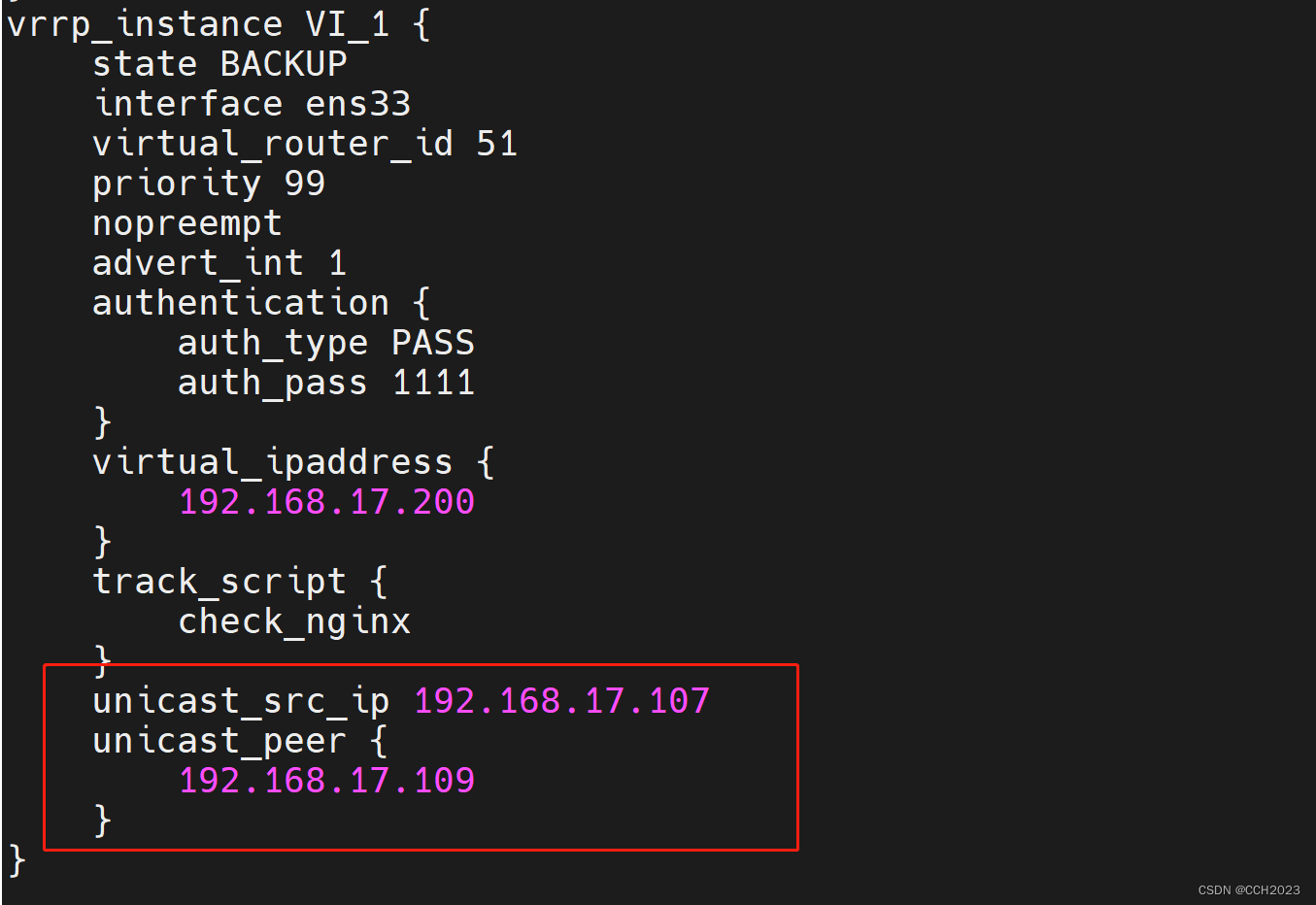
企业架构LNMP学习笔记27
Keepalived的配置补充: 脑裂(裂脑):vip出现在了多台机器上。网络不通畅,禁用了数据包,主备服务器没法通讯,造成备服务器认为主服务器不可用,绑定VIP,主服务器VIP不会释放…...

品牌策划经理工作内容|工作职责|品牌策划经理做什么?
一位美国作家曾说过“品牌是一系列期望、记忆、故事和关系,他们共同构成了消费者最终原则一个产品或者服务的原因。” 所以,品牌经理这个岗位主要是创造感知价值主张,激发消费者购买这个品牌后带来的感知价值,这种回报的本质相对…...
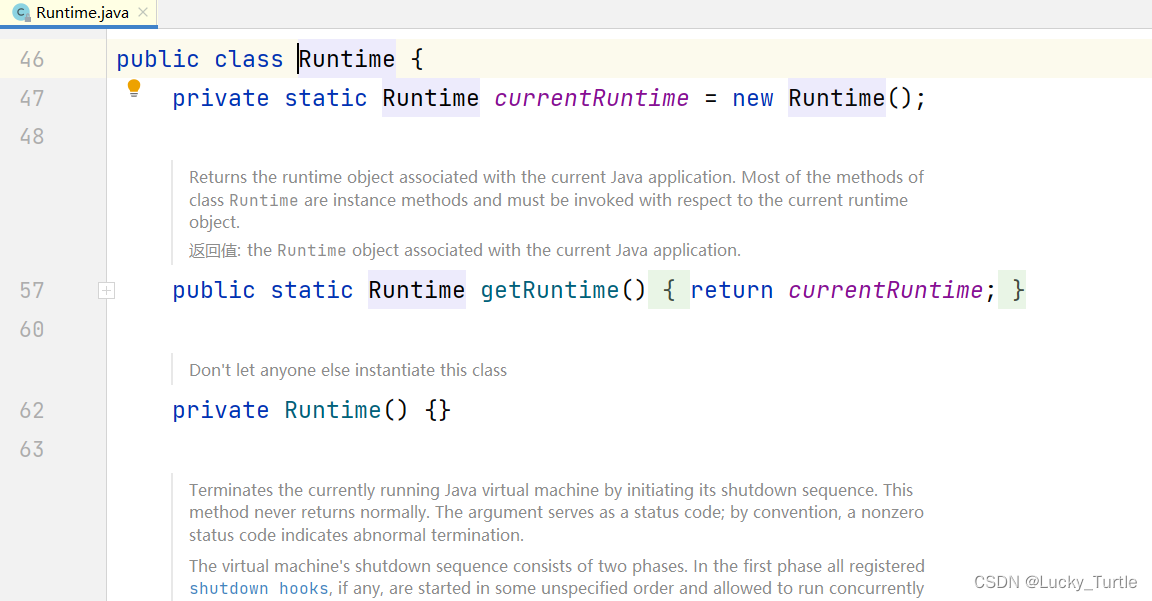
【设计模式】三、概述分类+单例模式
文章目录 概述设计模式类型 单例模式饿汉式(静态常量)饿汉式(静态代码块)懒汉式(线程不安全)懒汉式(线程安全,同步方法)懒汉式(线程安全,同步代码块)双重检查静态内部类枚举单例模式在 JDK 应用的源码分析 …...

手把手教学 Springboot+ftp+下载图片
简单教学,复制即用的Ftp下载图片 引入配置包 <dependency><groupId>commons-fileupload</groupId><artifactId>commons-fileupload</artifactId><version>1.3.1</version></dependency><dependency><grou…...

LaaS LLM as a service
LaaS LLM as a service 核心构成GPT 产业链如何进行商业化LLM(Large Language Model) 发展和趋势LLM(Large Language Model) 对于行业公司的分层LLM(Large Language Model) 的机遇和挑战 LaaS LLM as a service 核心构成 计算:算力模型:算法输入&…...

数据结构与算法(一)数组的相关概念和底层java实现
一、前言 从今天开始,笔者也开始从0学习数据结构和算法,但是因为这次学习比较捉急,所以记录的内容并不会过于详细,会从基础和底层代码实现以及力扣相关题目去写相关的文章,对于详细的概念并不会过多讲解 二、数组基础…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...
