【C++】AVL树的插入操作实现以及验证是否正确(带平衡因子)
文章目录
- 前言
- 一、AVL树结点的定义
- 二、AVL树的插入(Insert)
- 插入完整代码:
- 1.左单旋(RotateL)
- 2.右单旋(RotateR)
- 3.先右单旋再左单旋(RotateRL)
- 1.保存的bf为0
- 2.保存的bf为1
- 3.保存的bf为-1
- 4.先左单旋再右单旋(RotateLR)
- 三、AVL树的验证
前言
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
1.它的左右子树都是AVL树
2.左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在 O ( l o g 2 n ) O(log_2 n) O(log2n),搜索时间复杂度O( l o g 2 n log_2 n log2n)。
一、AVL树结点的定义
template<class K,class V>
//我们这里用键值的数据类型来举例
struct AVLTreeNode {pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;//(父结点)int _bf;//(平衡因子大小)AVLTreeNode(const pair<K, V>& kv)//构造函数:_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};
二、AVL树的插入(Insert)
AVL树的插入过程可以分为两步:
- 按照二叉搜索树的方式插入新节点
- 调整节点的平衡因子

插入完整代码:
typedef AVLTreeNode<K, V> Node;
bool Insert(const pair<K, V>& kv) {if (_root == nullptr) {//若为空树就先建立结点_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur) {//寻找要插入结点的父亲的位置if (cur->_kv.first < kv.first) {parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first) {parent = cur;cur = cur->_left;}else {return false;}}cur = new Node(kv);//找到要插入结点父亲后,寻找插入其左边还是右边if (parent->_kv.first < kv.first) {parent->_right = cur;}else {parent->_left = cur;}cur->_parent = parent;while (parent) {//更新平衡因子if (parent->_left == cur) {parent->_bf--;}else {parent->_bf ++ ;}// 更新后检测双亲的平衡因子if (parent->_bf == 0) {break;}else if (parent->_bf == 1 || parent->_bf == -1) {// 插入前双亲的平衡因子是0,插入后双亲的平衡因为为1 或者 -1 ,说明以双亲//为根的二叉树的高度增加了一层,因此需要继续向上调整cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2) {// 双亲的平衡因子为正负2,违反了AVL树的平衡性,需要对以parent// 为根的树进行旋转处理if (parent->_bf == 2 && cur->_bf == 1) {RotateL(parent);//左单旋}else if (parent->_bf == -2 && cur->_bf == -1) {RotateR(parent);//右单旋}else if (parent->_bf == 2 && cur->_bf == -1) {RotateRL(parent);//双旋}else if (parent->_bf == -2 && cur->_bf == 1) {RotateLR(parent);//双旋}break;}else {assert(false);}}return true;}
1.左单旋(RotateL)
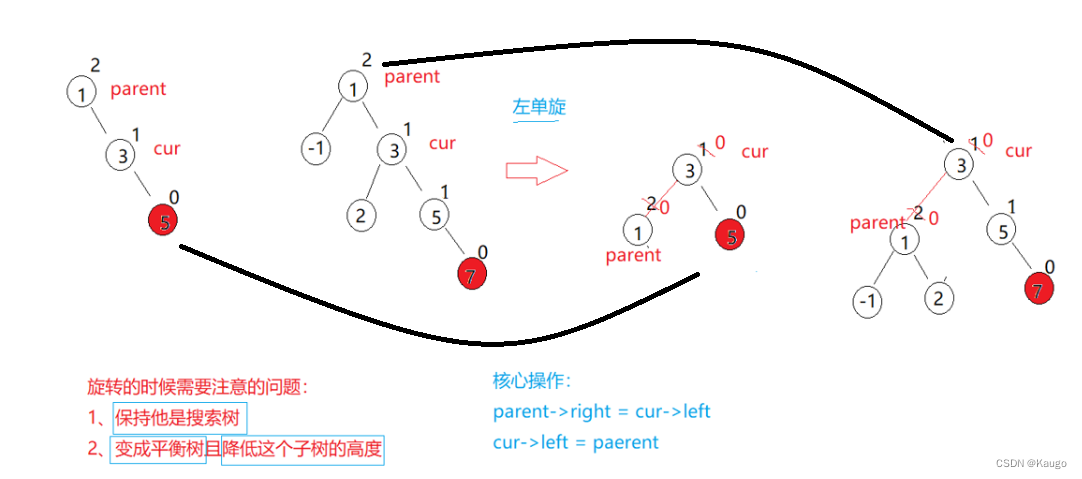
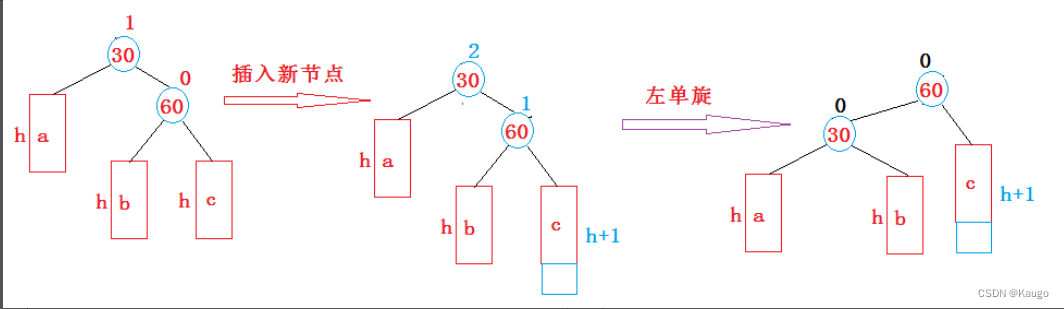
void RotateL(Node* parent) {Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;// 核心操作if (curleft) {//因为curleft可能为空curleft->_parent = parent;}Node* ppnode = parent->_parent;//提前记录下父结点的父亲cur->_left = parent;// 核心操作parent->_parent = cur;if (ppnode == nullptr) {//判断原先parent是否为根节点//因为根节点的父亲为空_root = cur;cur->_parent = nullptr;}else {//说明parent不为根节点//parent可能为ppnode的左或者右子树,改变ppnode的指向if (ppnode->_left == parent) {ppnode->_left = cur;}else {ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;// 根据调整后的结构更新部分节点的平衡因子}
2.右单旋(RotateR)
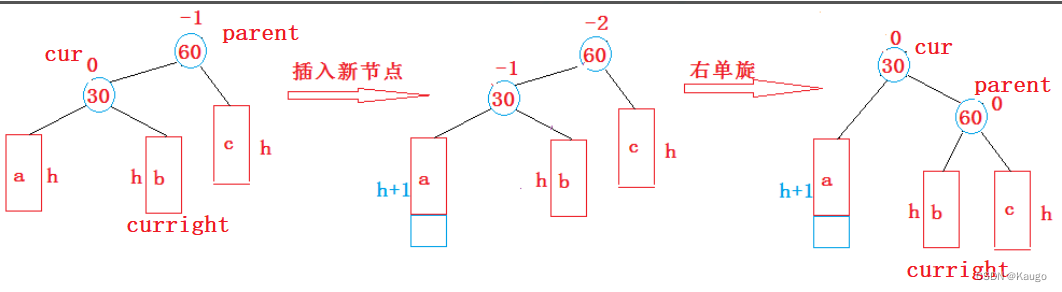
void RotateR(Node* parent) {Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;if (curright) {//因为curleft可能为空curright->_parent = parent;}cur->_right = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (ppnode == nullptr) {//判断原先parent是否为根节点//因为根节点的父亲为空_root = cur;cur->_parent = nullptr;}else {//说明parent不为根节点//parent可能为ppnode的左或者右子树,改变ppnode的指向if (ppnode->_left == parent) {ppnode->_left = cur;}else {ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;// 根据调整后的结构更新部分节点的平衡因子}
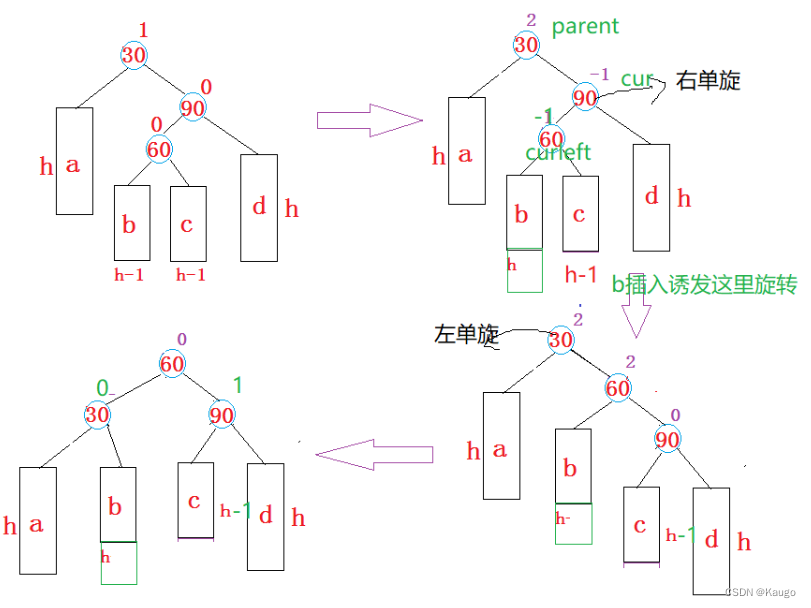
3.先右单旋再左单旋(RotateRL)
以cur为旋转点进行右旋,以parent为旋转点进行左旋,之后进行平衡因子的修改
void RotateRL(Node* parent) {Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->_bf;// 旋转之前,保存curleft的平衡因子,旋转完成之后,需要根据该平衡因子来调整其他节//点的平衡因子RotateR(cur);RotateL(parent);if (bf == 0) {cur->_bf = 0;curleft->_bf = 0;parent->_bf = 0;}else if (bf == 1) {cur->_bf = 0;curleft->_bf = 0;parent->_bf = -1;}else if (bf == -1){cur->_bf = 1;curleft->_bf = 0;parent->_bf = 0;}else{assert(false);}}
1.保存的bf为0
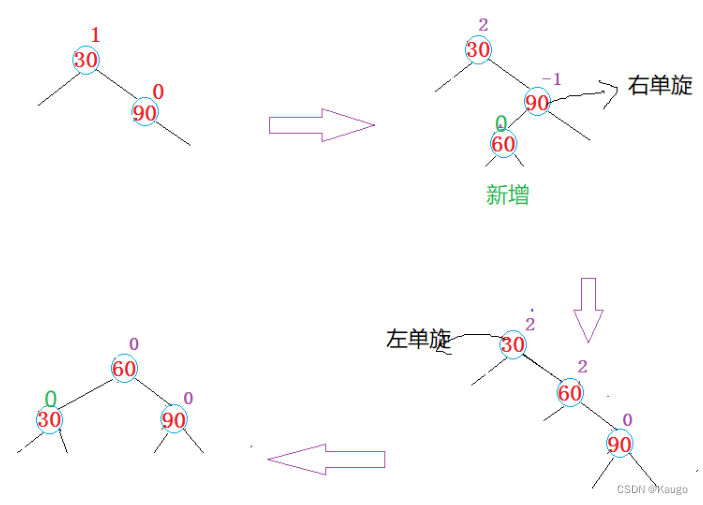
2.保存的bf为1
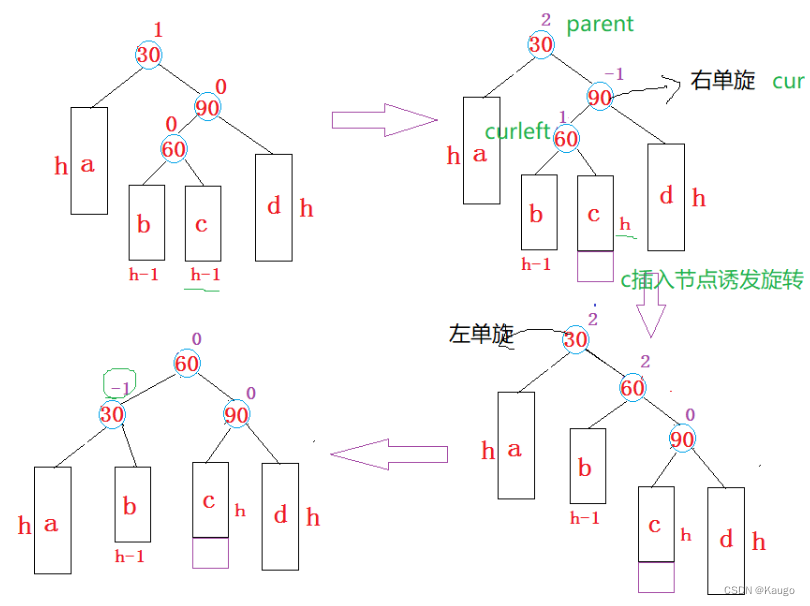
3.保存的bf为-1
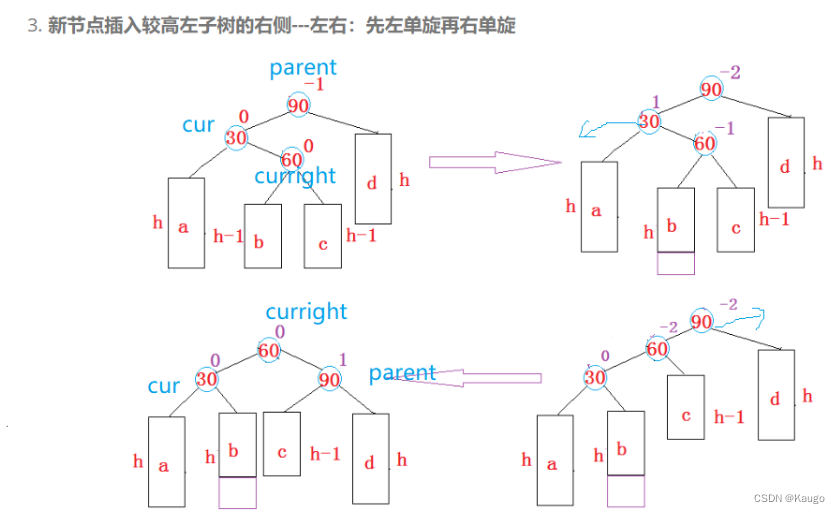
4.先左单旋再右单旋(RotateLR)
以cur为旋转点进行左旋,以parent为旋转点进行右旋,之后进行平衡因子的修改
void RotateLR(Node* parent) {Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;// 旋转之前,保存curright的平衡因子,旋转完成之后,需要根据该平衡因子来调整其他节//点的平衡因子RotateL(cur);RotateR(parent);if (bf == 0) {cur->_bf = 0;parent->_bf = 0;curright->_bf = 0;}else if (bf == -1){parent->_bf = 1;cur->_bf = 0;curright->_bf = 0;}else if (bf == 1){parent->_bf = 0;cur->_bf = -1;curright->_bf = 0;}else {assert(false);}}
三、AVL树的验证
验证其为平衡树关键点:
1.每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
2.节点的平衡因子是否计算正确
int Height(Node* root) {if (root == nullptr) {return 0;}int left = Height(root->_left);int right = Height(root->_right);return left > right ? left + 1 : right + 1;}bool IsBalance() {return IsBalance(_root);}bool IsBalance(Node* root) {if (root == nullptr) {return true;}int left = Height(root->_left);int right = Height(root->_right);if (right - left != root->_bf) {//节点的平衡因子是否计算正确cout << "平衡因子异常" << root->_kv.first << "=>" << root->_bf << endl;return false;}//每个节点子树高度差的绝对值不超过1//之后在验证左右子树return abs(right-left)<2&&IsBalance(root->_left) && IsBalance(root->_right);}
相关文章:

【C++】AVL树的插入操作实现以及验证是否正确(带平衡因子)
文章目录 前言一、AVL树结点的定义二、AVL树的插入(Insert)插入完整代码:1.左单旋(RotateL)2.右单旋(RotateR)3.先右单旋再左单旋(RotateRL)1.保存的bf为02.保存的bf为13…...
【Linux-Day10-信号量,共享内存,消息队列】
信号量 信号量描述 信号量是一个特殊的变量,一般取正数值。它的值代表允许访问的资源数目,获取资源 时,需要对信号量的值进行原子减一,该操作被称为 P 操作。 当信号量值为 0 时,代表没有资源可用,P 操作…...
使用IntelliJ IDEA本地启动调试Flink流计算工程的2个异常解决
记录:471 场景:使用IntelliJ IDEA本地启动调试Flink流计算时,报错一:加载DataStream报错java.lang.ClassNotFoundException。报错二:No ExecutorFactory found to execute the application。 版本:JDK 1.…...
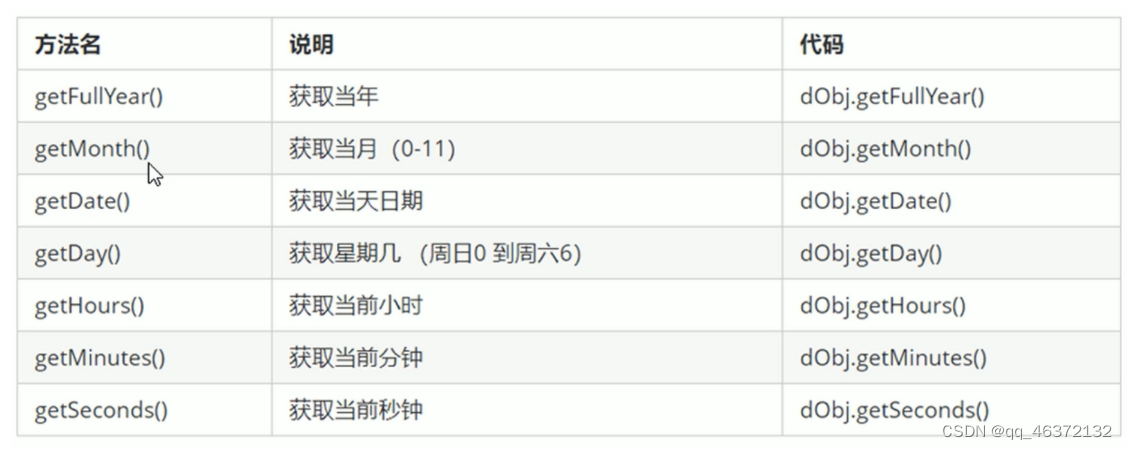
对象及日期对象
对象 1.什么是对象 类是对象的抽象,对象是类的实例 程序算法数据结构 万物皆对象,对象是一个具体的事物,看到见摸得着,对象是一组无序相关属性和方法的集合(无序,所以对象没有length属性),所有事物都是对象,列如字符串,数值,数组,函数等. 属性:事物的特征,在对象中用属性表…...

鼠标滚轮编码器解析
文章目录 前言一、鼠标滚轮编码器逻辑?二、使用步骤 1.引入库2.读入数据总结 前言 鼠标滚轮编码器为三脚接入,一个COM脚C(一般是接地),两个脉冲波形输入脚A、B,转动滚轮编码器会在两个脉冲输入脚上产生脉冲…...
【PTA】攀拓(PAT)- 程序设计(甲级)2023年春季考试
个人学习记录,代码难免不尽人意。 今天又斥资买了今年春季的真题一试,呃,感觉尽力了,89分,在当年排名23,感觉还不错,没有出现读不懂的题目和没有思路的情况,扣的11分分别是第二题两个…...

Spring Cloud Gateway 实现原理
Spring Cloud Gateway是Spring Cloud生态系统中的一个组件,用于构建基于Spring Boot的微服务架构中的网关服务。它的主要目的是提供一种灵活的方式来路由、过滤和转换HTTP请求,从而允许您构建强大、高性能的微服务应用程序。 以下是Spring Cloud Gatewa…...

嘉泰实业:真实低门槛,安全有保障
在互联网金融大行其道的当下,无论用户是多么的青睐、喜爱这种便捷的理财方式,也一定得把资金安全放在心上。要投就投那些实力背景雄厚,诚信经营的平台,可以选择投资用户基数庞大的理财老品牌,也可以选择发展势头迅猛的…...

spring boot 2.7 -> 3.0升级指南
spring boot提供一个版本迁移指南 2.7 -> 3.0...

MQTT 连接优化指南
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

算法和数据结构学习中的一些小的工具函数
算法和数据结构学习中的一些小的工具函数 作者:Grey 原文地址: 博客园:算法和数据结构学习中的一些小的工具函数 CSDN:算法和数据结构学习中的一些小的工具函数 提取一个数二进制最右侧的 1 比如二进制为:0100 0…...

解决2K/4K高分屏下Vmware等虚拟机下Kail Linux界面显示问题
问题现象 在我们日常使用VirtualBox、Vmware workstation、Hyper-V等虚拟机安装使用Kali系统,在2K/4K高分辨率电脑下Kali系统界面显示太小,包括各种软件及命令终端字体均无法很直观的看出,影响我们的正常测试及使用。 常规处理思路 很多人…...

【校招VIP】java语言考点之双亲委派模型
考点介绍: 双亲委派是校招面试中的高频考点之一。双亲委派机制定义: 当一个类加载器收到了类加载的请求的时候,他不会直接去加载指定的类,而是把这个请求委托给自己的父加载器去加载,只有父加载器无法加载这个类的时候࿰…...

2023年阿里云新用户云服务器价格表
阿里云,作为国内领先的云计算服务提供商,一直致力于为全球用户提供安全、稳定、高效的云计算服务。对于新用户来说,阿里云服务器是一个非常不错的选择。那么,阿里云新用户云服务器的价格是怎样的呢?本文将为大家详细介…...

信号相关名词概念汇总-采样周期、泄露、窗函数等
信号相关名词概念汇总-采样周期、泄露、窗函数等 以下为信号相关名词概念的汇总 1 名词解释 采样周期/间隔:采样频率的倒数,两次相邻采样之间的时间间隔采样时间:采样的总时长,即采样点数N和采样周期的乘积采样频率: …...
数字化新零售营销模式如何落地?数字化新零售营销功能推荐
通过科技手段,针对对线下零售店面的客户进行消费行为、频次等的分析,并进一步整合线上线下资源,实现实体零售的效率充分化,便是目前很火的新零售营销模式,能够将实体门店与数字化技术进行有机结合,通过为…...

712. 两个字符串的最小ASCII删除和 -- 动规
712. 两个字符串的最小ASCII删除和 class MinimumDeleteSum:"""712. 两个字符串的最小ASCII删除和https://leetcode.cn/problems/minimum-ascii-delete-sum-for-two-strings/"""def solution(self, s1: str, s2: str) -> int:""&qu…...

python中的小tips
1、注释 1、注释快捷键: Ctrl/ 可以注释掉光标所在的这一行,或者是选中的区域。 对于注释掉的这一行或者这一区域,按下ctrl/则会去掉注释。 2、多行注释 在写多行注释时,英文状态下写三个",会自动变成六个"&…...

高精度(加减乘除)
高精度算法出现的原因 当参与运算的数的范围大大的超出了标准数据类型,如int(-2147483648 ~ 2147483647)或者long long的范围,就需要使用高精度算法来进行数的运算。高精度运算的特点是代码长度比较长,本质是对数学运算…...
java企业数据管理系统
项目介绍 此项目为企业数据管理系统的后端部分,前端部分请参考vue-admin,项目实现了菜单管理、用户管理、角色管理和权限管理四个基础模块,前端菜单管理结合动态路由可自由添加菜单。结合Shiro权限管理实现了菜单和按钮的权限控制。 ❝ 前端…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
