R语言中的数据结构----矩阵
目录
(1)创建矩阵
(2) 线性代数运算
(3)矩阵索引
(4)矩阵元素的筛选
(5)增加或删除矩阵的行或列
(6)apply()函数
(7)矩阵和向量的区别
(8)避免意外降维
(9)矩阵行和列的命名
(10)高维数组
矩阵的基本操作
#将c(1,4)和c(1,2)两个向量绑定起来
> m<-rbind(c(1,4),c(2,2))
> m[,1] [,2]
[1,] 1 4
[2,] 2 2
#计算向量(1,1)和m的矩阵积
> m%*%c(1,1)[,1]
[1,] 5
[2,] 4
#第一行第二列
> m[1,2]
[1] 4
#第二行第二列
> m[2,2]
[1] 2
#第一行
> m[1,]
[1] 1 4
#第二列
> m[,2]
[1] 4 2
> (1)创建矩阵
法一
> y<-matrix(c(1,2,3,4),nrow=2,ncol=2)
> y[,1] [,2]
[1,] 1 3
[2,] 2 4
#可以只定义nrow和ncol中的一个
> y<-matrix(c(1,2,3,4),nrow=2)
> y[,1] [,2]
[1,] 1 3
[2,] 2 4
#表示创建矩阵第二列
> y[,2]
[1] 3 4法二
#byrow参数设置为TRUE,使矩阵元素按行排列
> m<-matrix(c(1,2,3,4,5,6),nrow=2,byrow=T)
> m[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6y<-matrix(nrow=2,ncol = 2)
> y[1,1]<-1
> y[2,1]<-2
> y[1,2]<-3
> y[2,2]<-4
> y[,1] [,2]
[1,] 1 3
[2,] 2 4(2) 线性代数运算
#矩阵相乘
> y%*%y[,1] [,2]
[1,] 7 15
[2,] 10 22
#矩阵数量乘法
> 3*y[,1] [,2]
[1,] 3 9
[2,] 6 12
#矩阵加法
> y+y[,1] [,2]
[1,] 2 6
[2,] 4 8(3)矩阵索引
•使用逗号,分隔行和列索引来访问矩阵中的元素
# 创建一个3x3的矩阵
mat <- matrix(1:9, nrow = 3)
mat# 访问特定元素
mat[2, 3] # 访问第2行第3列的元素,输出为6#也可以使用
> "["(z,3,2)
[1] 7
#"["相当于一个函数# 访问整行或整列
mat[1, ] # 访问第1行的所有元素,输出为 1 4 7
mat[, 2] # 访问第2列的所有元素,输出为 2 5 8# 访问多行或多列
mat[2:3, ] # 访问第2行和第3行的所有元素
mat[, c(1, 3)] # 访问第1列和第3列的所有元素
•使用逻辑向量来选择满足特定条件的行或列
# 创建一个3x3的矩阵
mat <- matrix(1:9, nrow = 3)
mat# 使用逻辑向量进行索引
mat[mat > 5] # 选择大于5的元素,输出为 6 7 8 9
mat[mat[, 2] > 3, ] # 选择第2列大于3的行的所有元素
•对一个矩阵的子矩阵进行赋值
> y<-matrix(c(1:6),nrow=3)
> y[,1] [,2]
[1,] 1 4
[2,] 2 5
[3,] 3 6
#第一行和第三行赋值
> y[c(1,3),]<-matrix(c(1,1,8,12),nrow=2)
> y[,1] [,2]
[1,] 1 8
[2,] 2 5
[3,] 1 12> x<-matrix(nrow=3,ncol=3)
> y<-matrix(c(4,5,2,3),nrow=2)
> y[,1] [,2]
[1,] 4 2
[2,] 5 3
> x[2:3,2:3]<-y
> x[,1] [,2] [,3]
[1,] NA NA NA
[2,] NA 4 2
[3,] NA 5 3(4)矩阵元素的筛选
> x<-matrix(c(1,2,3,2,3,4),nrow=3)
> x[,1] [,2]
[1,] 1 2
[2,] 2 3
[3,] 3 4
#判断第二列元素是否>=3,若>=3,则输出
> x[x[,2]>=3,][,1] [,2]
[1,] 2 3
[2,] 3 4
逐步分解为
> j<-x[,2]>=3
> j
[1] FALSE TRUE TRUE
#x[j,]的行与向量j中的取值为TRUE的行对应
> x[j,][,1] [,2]
[1,] 2 3
[2,] 3 4> x<-matrix(c(1:6),nrow=3)
> x[,1] [,2]
[1,] 1 4
[2,] 2 5
[3,] 3 6
> z<-c(5,12,13)
#z%%2==1用于判断z的每个元素是否是奇数,返回的结果是(TRUE,FALSE,TRUE)
#因此我们提取第1,3行的数据
> x[z%%2==1,][,1] [,2]
[1,] 1 4
[2,] 3 6
注意:如果写为以下形式,就不是以矩阵形式显示了
>x[z%%2==1]
[1] 1 3 4 6> x[,1] [,2]
[1,] 1 4
[2,] 2 5
[3,] 3 6
#这里用了&,表示两个条件都需要判断
> x[x[,1]>1 & x[,2]>5,]
[1] 3 6#which(m>2)来查找矩阵m中大于2的元素的索引
> m<-matrix(c(5,2,9,-1,10,11),nrow=3)
> m[,1] [,2]
[1,] 5 -1
[2,] 2 10
[3,] 9 11
> which(m>2)
[1] 1 3 5 6
#m的1,3,5,6个元素大于2(5)增加或删除矩阵的行或列
> x<-c(12,5,13,16,8)
> x
[1] 12 5 13 16 8
> x<-c(x,20)
> x
[1] 12 5 13 16 8 20
> x<-c(x[1:3],20,x[4:6])
> x
[1] 12 5 13 20 16 8 20
> x<-x[-2:-4]
> x
[1] 12 16 8 20
> one<-c(1,1,1,1)
> z<-matrix(c(1,2,3,4,1,1,0,0,1,0,1,0),nrow=4)
> z[,1] [,2] [,3]
[1,] 1 1 1
[2,] 2 1 0
[3,] 3 0 1
[4,] 4 0 0
> cbind(one,z)one
[1,] 1 1 1 1
[2,] 1 2 1 0
[3,] 1 3 0 1
[4,] 1 4 0 0#1被循环补齐为由4个1组成的列向量
> cbind(1,z)[,1] [,2] [,3] [,4]
[1,] 1 1 1 1
[2,] 1 2 1 0
[3,] 1 3 0 1
[4,] 1 4 0 0#和创建向量一样,创建一个新的矩阵很消耗时间
> q<-cbind(c(1,2),c(3,4))
> q[,1] [,2]
[1,] 1 3
[2,] 2 4#可以通过重新赋值来删除矩阵的行或列
> m<-matrix(1:6,nrow=3)
> m[,1] [,2]
[1,] 1 4
[2,] 2 5
[3,] 3 6> m<-m[c(1,3),]
> m[,1] [,2]
[1,] 1 4
[2,] 3 6
(6)apply()函数
apply()函数的格式
apply(m,dimcode,f,farge)
m代表一个矩阵
dimcode表示维度代码,1表示每一行应用函数,2表示每一列应用函数
f是应用在行,列上的函数
farge是f的可选参数集
> z<-matrix(c(1:6),nrow = 3)
> z[,1] [,2]
[1,] 1 4
[2,] 2 5
[3,] 3 6
> apply(z,2,mean)
#或者可以直接使用colMeans
> colMeans(z)
[1] 2 5这里的f可以是自定义函数
> f<-function(x){
+ return(x/c(2,8))
+ }
> y<-apply(z,1,f)
> y[,1] [,2] [,3]
[1,] 0.5 1.000 1.50
[2,] 0.5 0.625 0.75fargs表示可选参数集
> copymag<-function(rw,d){
#向量每个元素对应矩阵的每行,如果该行前d个元素中1较多,向量对应元素就取1,反之取0
+ maj<-sum(rw[1:d])/d
+ return(if(maj>0.5)1 else 0)
+ }
> x<-matrix(c(1,1,1,0,0,1,0,1,1,1,0,1,1,1,1,1,0,0,1,0),nrow = 4)
> x[,1] [,2] [,3] [,4] [,5]
[1,] 1 0 1 1 0
[2,] 1 1 1 1 0
[3,] 1 0 0 1 1
[4,] 0 1 1 1 0
> apply(x,1,copymag,3)
[1] 1 1 0 1> apply(x,1,copymag,2)
[1] 0 1 0 0
#这里的3,2是函数copymaj()中形式参数d的实际取值,矩阵的第一行是(1,0,1,1,0),当d取3时,前3个是(1,0,1),1占多数,则copymag返回1,第一个元素为1,其他以此类推> apply(x,2,copymag,2)
[1] 1 0 1 1 0(7)矩阵和向量的区别
> z<-matrix(c(1:8),nrow = 4)
> z[,1] [,2]
[1,] 1 5
[2,] 2 6
[3,] 3 7
[4,] 4 8
#z作为1个向量,可以求他的长度
> length(z)
[1] 8#z也是一个矩阵,有矩阵的性质
> dim(z)
[1] 4 2
> nrow(z)
[1] 4
> ncol(z)
[1] 2#得到矩阵的行数和列数,[1]显示行数,[2]显示列数
> nrow<-function(x)
+ dim(x)[1]
> nrow(z)
[1] 4
> (8)避免意外降维
> z[,1] [,2]
[1,] 1 5
[2,] 2 6
[3,] 3 7
[4,] 4 8
> r<-z[2,]
> r
[1] 2 6
#这里的r是一个长度为2的向量,而不是一个1*2的矩阵,所以出现了降维,如何避免降维呢可以用以下方法验证
> attributes(z)
$dim
[1] 4 2> attributes(r)
NULL
> str(z)int [1:4, 1:2] 1 2 3 4 5 6 7 8
> str(r)int [1:2] 2 6可以用drop()参数
> r<-z[2,,drop=FALSE]
#r是一个1*2的矩阵
> r[,1] [,2]
[1,] 2 6
> dim(r)
[1] 1 2
(9)矩阵行和列的命名
> z<-matrix(c(1:4),nrow = 2)
> z[,1] [,2]
[1,] 1 3
[2,] 2 4
> colnames(z)
NULL
> colnames(z)<-c("a","b")
> za b
[1,] 1 3
[2,] 2 4
> colnames(z)
[1] "a" "b"
> z[,"a"]
[1] 1 2(10)高维数组
> firsttest<-matrix(c(46,21,50,30,25,48),nrow=3)
> secondtest<-matrix(c(46,41,50,43,35,49),nrow=3)> test<-array(data=c(firsttest,secondtest),dim=c(3,2,2))#共有2层,每层分别是3行2列
> attributes(test)
$dim
[1] 3 2 2#学生3第一次考试,第二部分的得分
> test[3,2,1]
[1] 48
#逐层显示
> print(test)
, , 1[,1] [,2]
[1,] 46 30
[2,] 21 25
[3,] 50 50, , 2[,1] [,2]
[1,] 46 43
[2,] 41 35
[3,] 50 50相关文章:

R语言中的数据结构----矩阵
目录 (1)创建矩阵 (2) 线性代数运算 (3)矩阵索引 (4)矩阵元素的筛选 (5)增加或删除矩阵的行或列 (6)apply()函数 (…...
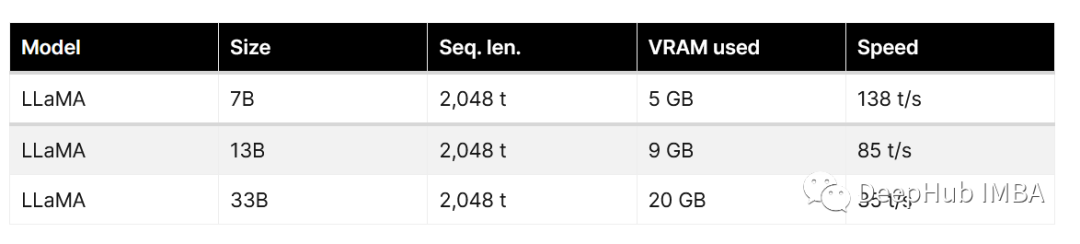
Llama-2 推理和微调的硬件要求总结:RTX 3080 就可以微调最小模型
大语言模型微调是指对已经预训练的大型语言模型(例如Llama-2,Falcon等)进行额外的训练,以使其适应特定任务或领域的需求。微调通常需要大量的计算资源,但是通过量化和Lora等方法,我们也可以在消费级的GPU上…...

C++多线程的用法(包含线程池小项目)
一些小tips: 编译命令如下: g 7.thread_pool.cpp -lpthread 查看运行时间: time ./a.out 获得本进程的进程id: this_thread::get_id() 需要引入的库函数有: #include<thread> // 引入线程库 #include<mutex> //…...
react ant ice3 实现点击一级菜单自动打开它下面最深的第一个子菜单
1.问题 默认的如果没有你的菜单结构是这样的: [{children: [{name: "通用配置"parentId: "1744857774620672"path: "basic"}],name: "系统管理"parentId: "-1"path: "system"} ]可以看到每层菜单的p…...

关于 Qt串口不同电脑出现不同串口号打开失败 的解决方法
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/132842297 红胖子(红模仿)的博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV、OpenGL、ffmpeg、OSG、单片机、软…...
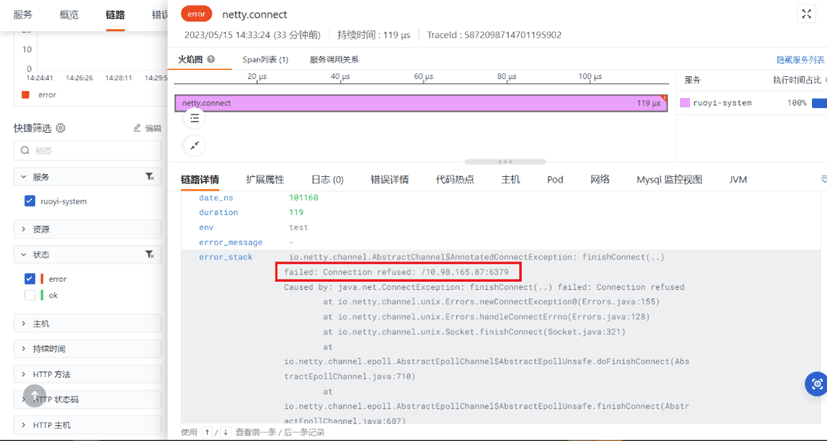
可观测性在灰度发布中的应用
前言 随着云计算的发展、云原生时代的来临,企业数字化转型进程不断深入,应用开发也越来越多地基于微服务化模式,快速迭代的能力使得应用开发更高效、更灵活。同时,也不得不面临应用版本快速升级所带来的的巨大挑战。 传统的发布方…...
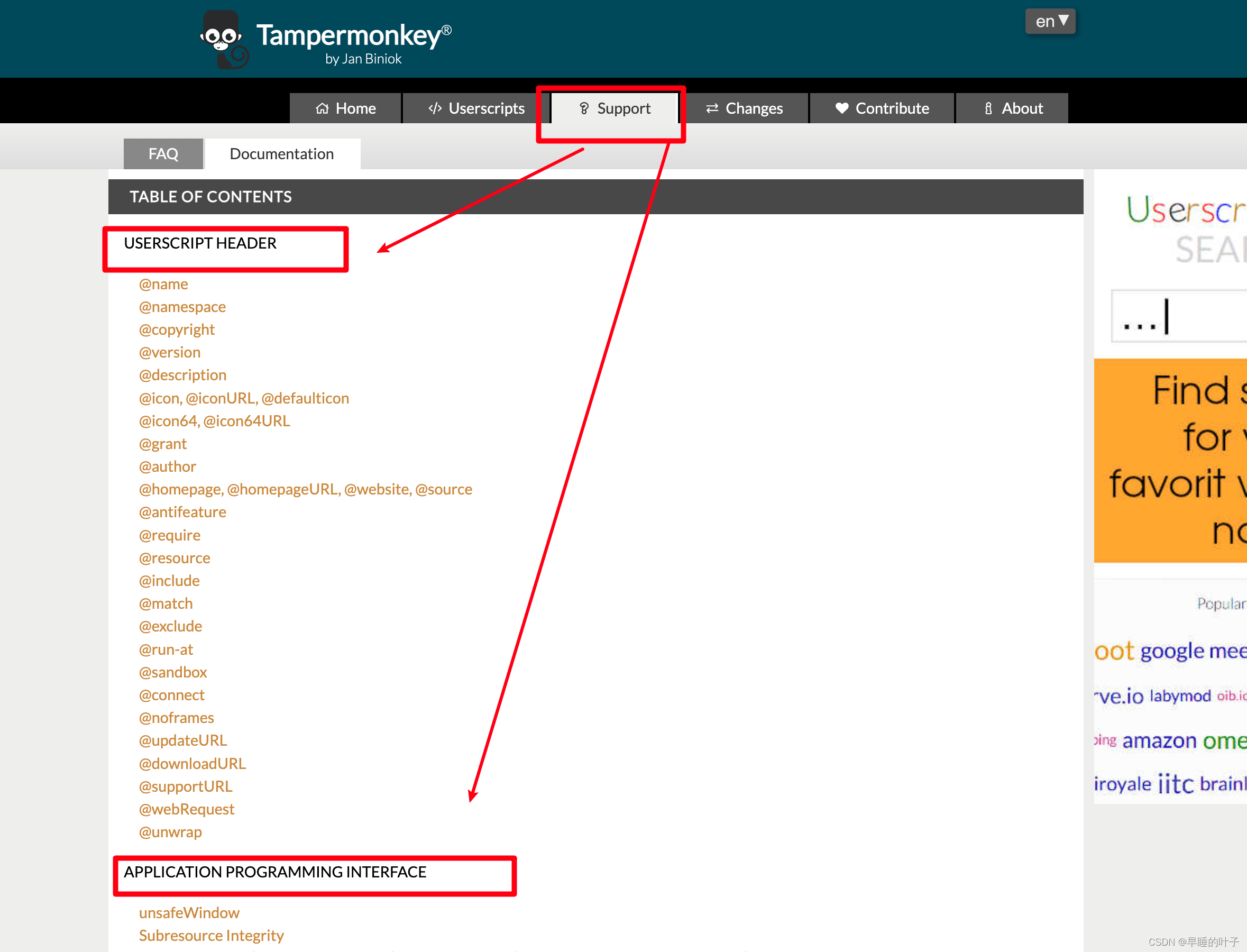
vscode开发油猴插件环境配置指南
文章目录 一、环境配置1.1油猴插件开始编写代码1.2油猴插件配置1.2.1浏览器插件权限1.2.2插件自身权限 2. 油猴脚本API学习2.1 头文件2.2 油猴API 一、环境配置 1.1油猴插件开始编写代码 在vscode 中写入如下代码‘ // UserScript // name cds_test // namespace …...
网站不收录没排名降权怎么处理-紧急措施可恢复网站
网站降权对于SEO人员来说是非常致命的打击,因为网站一旦被搜索引擎降权,排名会严重地下降,网站的流量也会大幅下降,直接影响到收益。而且处理不好的话会导致恢复的时间周期无限拉长,所以网站被降权后我们要第一时间采取…...
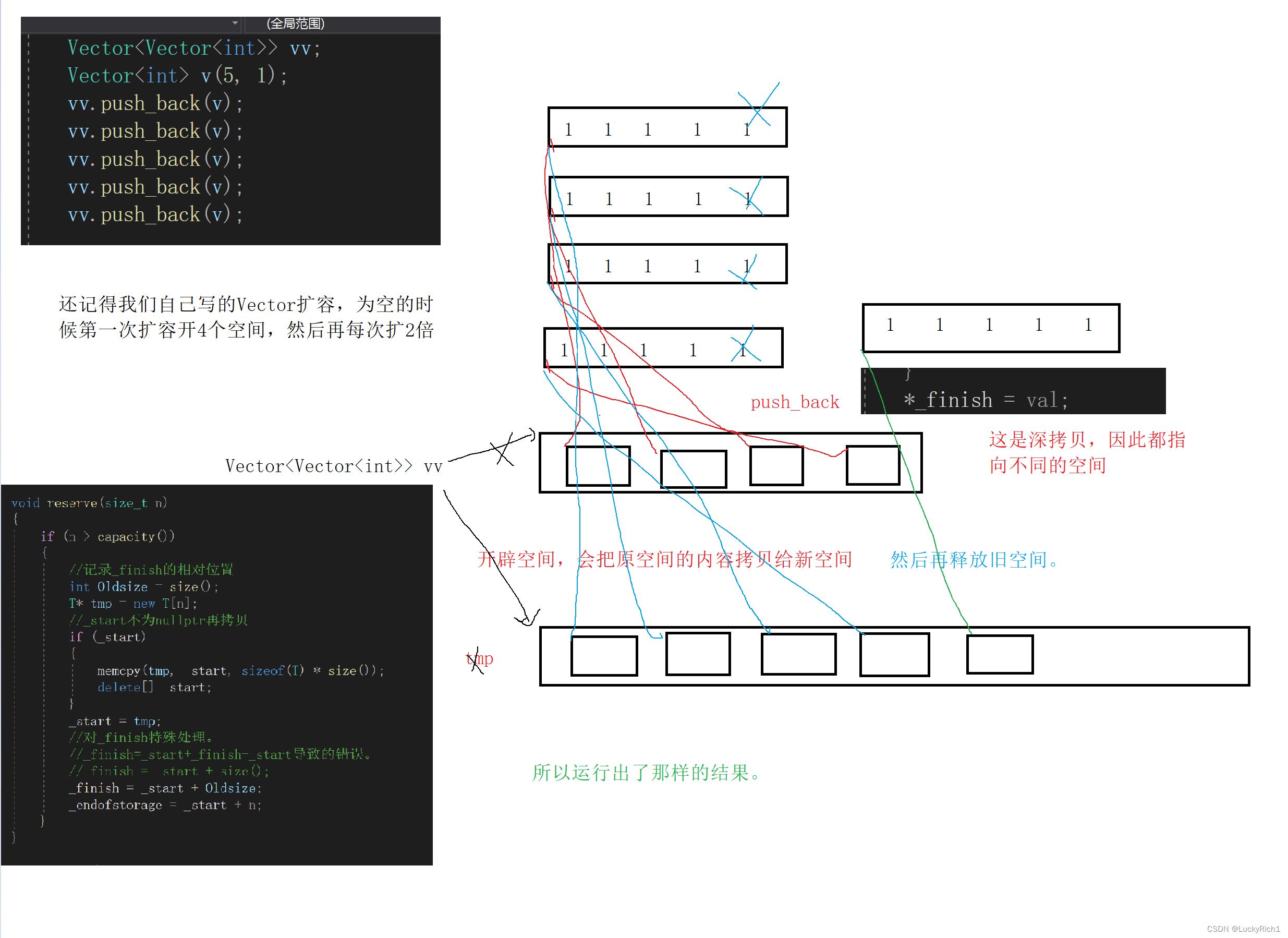
C++vector模拟实现
vector模拟实现 1.构造函数2.拷贝构造3.析构赋值运算符重载4.iterator5.modifiers5.1push_back5.2pop_back5.3empty5.4insert5.5erase5.6swap 6.Capacity6.1size6.2capacity6.3reserve6.4resize6.5empty 7.Element access7.1operator[]7.2at 8.在谈reserve vector官方库实现的是…...

《DATASET DISTILLATION》
这篇文章提出了数据浓缩的办法,在前面已有的知识浓缩(压缩模型)的经验上,提出了不压缩模型,转而压缩数据集的办法,在压缩数据集上训练模型得到的效果尽可能地接近原始数据集的效果。 摘要 模型蒸馏的目的是…...

GDPU 数据结构 天码行空1
1. 病历信息管理 实现病历查询功能。具体要求如下: 定义一个结构体描述病人病历信息(病历号,姓名,症状);完成功能如下: 输入功能:输入5个病人的信息; 查询功能:输入姓名,在5个病历中进行查找,如果找到则显示该人的信息,…...

【C++】红黑树的模拟实现
🌇个人主页:平凡的小苏 📚学习格言:命运给你一个低的起点,是想看你精彩的翻盘,而不是让你自甘堕落,脚下的路虽然难走,但我还能走,比起向阳而生,我更想尝试逆风…...
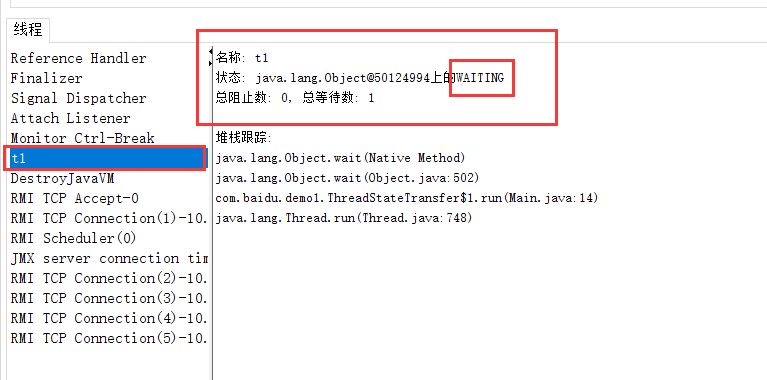
【多线程】Thread 类 详解
Thread 类 详解 一. 创建线程1. 继承 Thread 类2. 实现 Runnable 接口3. 其他变形4. 多线程的优势-增加运行速度 二. Thread 类1. 构造方法2. 常见属性3. 启动线程-start()4. 中断线程-interrupt()5. 线程等待-join()6. 线程休眠-sleep()7. 获取当前线程引用 三. 线程的状态1. …...

LINUX 网络管理
目录 一、NetworkManager的特点 二、配置网络 1、使用ip命令临时配置 1)查看网卡在网络层的配置信息 2)查看网卡在数据链路层的配置信息 3)添加或者删除临时的网卡 4)禁用和启动指定网卡 2、修改配置文件 3、nmcli命令行…...
refresh rate
1920 x 1080 显卡刷新率 60...

使用 NGINX Unit 实施应用隔离
原文作者:Artem Konev - Senior Technical Writer 原文链接:使用 NGINX Unit 实施应用隔离 转载来源:NGINX 中文官网 NGINX 唯一中文官方社区 ,尽在 nginx.org.cn NGINX Unit 特性集的最新动态之一是支持应用隔离,该特…...

2023/09/12 qtc++
实现一个图形类(Shape) ,包含受保护成员属性:周长、面积, 公共成员函数:特殊成员函数书写 定义一个圆形类(Circle) ,继承自图形类,包含私有属性:半径 公共成员函数:特殊成员函数…...
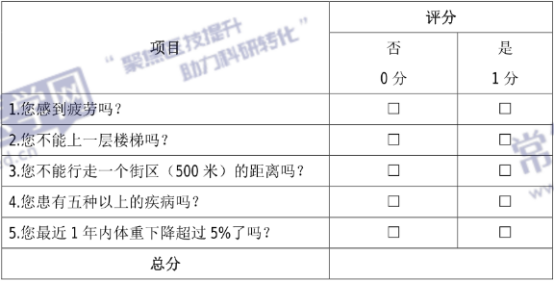
全科医学科常用评估量表汇总,建议收藏!
根据全科医学科医生的量表使用情况,笔者整理了10个常用的全科医学科量表,可在线评测直接出结果,可转发使用,可生成二维码使用,可创建项目进行数据管理,有需要的小伙伴赶紧收藏! 日常生活能力量表…...
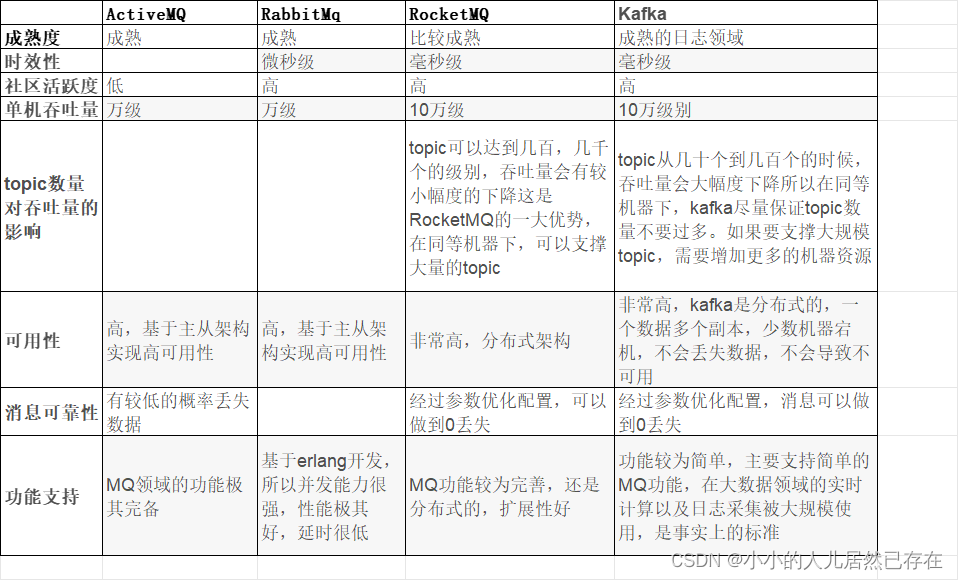
了解消息中间件的基础知识
为什么要使用消息中间件? 解耦:消息中间件可以使不同的应用程序通过解耦的方式进行通信,减少系统间的依赖关系提供异步通信:消息中间件可以实现异步消息传递,提高系统的响应性能。流量削峰:消息中间件可以…...
【linux】Linux wps字体缺失、加粗乱码解决
解决wps字体缺失问题 1、下载字体包 git clone https://github.com/iamdh4/ttf-wps-fonts.git2、创建单独放置字体的目录 mkdir /usr/share/fonts/wps-fonts3、复制字体到系统目录下 cp ttf-wps-fonts/* /usr/share/fonts/wps-fonts4、修改字体权限 chmod 644 /usr/share/f…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...
