【数据结构-堆】堆
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。
- 推荐:kuan 的首页,持续学习,不断总结,共同进步,活到老学到老
- 导航
- 檀越剑指大厂系列:全面总结 java 核心技术点,如集合,jvm,并发编程 redis,kafka,Spring,微服务,Netty 等
- 常用开发工具系列:罗列常用的开发工具,如 IDEA,Mac,Alfred,electerm,Git,typora,apifox 等
- 数据库系列:详细总结了常用数据库 mysql 技术点,以及工作中遇到的 mysql 问题等
- 懒人运维系列:总结好用的命令,解放双手不香吗?能用一个命令完成绝不用两个操作
- 数据结构与算法系列:总结数据结构和算法,不同类型针对性训练,提升编程思维,剑指大厂
非常期待和您一起在这个小小的网络世界里共同探索、学习和成长。💝💝💝 ✨✨ 欢迎订阅本专栏 ✨✨
博客目录
- 一.堆简介
- 1.什么是堆?
- 2.大顶堆
- 3.小顶堆
- 4.JDK 的优先队列
- 5.建堆
- 二.堆题目
- 1.堆排序
- 2.数组中第 K 大元素-力扣 215 题
- 3.数据流中第 K 大元素-力扣 703 题
- 4.数据流的中位数-力扣 295 题
一.堆简介
1.什么是堆?
堆(Heap)是一种重要的数据结构,通常用于实现优先队列和一些其他算法。堆具有以下主要特点:
-
完全二叉树结构: 堆通常是一个完全二叉树,这意味着树中的每个节点都有最多两个子节点,除了最后一层,其他层都是满的。这种特性使得堆可以有效地使用数组来表示,因为数组的索引操作非常高效。
-
堆序性质: 堆分为两种主要类型,最小堆和最大堆,它们都具有堆序性质。在最小堆中,每个节点的值都小于或等于其子节点的值,根节点的值最小。在最大堆中,每个节点的值都大于或等于其子节点的值,根节点的值最大。
-
堆的操作: 堆支持一些基本操作,包括插入元素、删除根节点(最小或最大元素)、查找根节点(最小或最大元素),以及堆化操作(将一个无序数组或树转化为堆)。这些操作的时间复杂度通常为 O(log n),其中 n 是堆中元素的数量。
-
应用: 堆广泛用于解决各种问题,如优先队列(用于任务调度、Dijkstra 算法等)、堆排序算法、求中位数、Top K 问题、图算法(Prim 和 Kruskal 算法中的最小生成树等)等。由于其高效的插入和删除操作,堆在这些问题中表现出色。
-
实现: 堆可以用数组来表示。在数组中,根节点通常位于索引 0,对于节点 i,其左子节点位于 2i + 1,右子节点位于 2i + 2。这种表示方法使得堆的操作更加高效。堆可以是最小堆或最大堆,具体类型取决于问题需求。
-
平衡性: 堆是一种自平衡数据结构,即在插入和删除操作后,堆仍然保持堆序性质。这是通过堆化操作来实现的,它可以向上(上滤)或向下(下滤)调整节点的位置,以满足堆的要求。
堆是一种非常有用的数据结构,用于解决许多与优先级相关的问题和算法。最小堆和最大堆的差异在于它们的堆序性质,但它们都具有相似的操作和实现方式。理解堆的基本原理和操作对于编写高效的算法非常重要。
2.大顶堆
以大顶堆为例,相对于之前的优先级队列,增加了堆化等方法
public class MaxHeap {int[] array;int size;public MaxHeap(int capacity) {this.array = new int[capacity];}/*** 获取堆顶元素** @return 堆顶元素*/public int peek() {//获取堆顶元素return array[0];}/*** 删除堆顶元素** @return 堆顶元素*/public int poll() {//获取堆顶元素int top = array[0];//交换堆顶和堆底swap(0, size - 1);//容量--size--;//堆顶下沉down(0);return top;}/*** 删除指定索引处元素** @param index 索引* @return 被删除元素*/public int poll(int index) {int deleted = array[index];swap(index, size - 1);size--;down(index);return deleted;}/*** 替换堆顶元素* @param replaced 新元素*/public void replace(int replaced) {array[0] = replaced;down(0);}/*** 堆的尾部添加元素** @param offered 新元素* @return 是否添加成功*/public boolean offer(int offered) {if (size == array.length) {return false;}up(offered);size++;return true;}// 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶private void up(int offered) {//默认插入位置在最后的indexint child = size;while (child > 0) {//父节点的位置int parent = (child - 1) / 2;//上浮if (offered > array[parent]) {array[child] = array[parent];} else {break;}//把父节点的坐标给childchild = parent;}//不要忘了赋值array[child] = offered;}public MaxHeap(int[] array) {this.array = array;this.size = array.length;heapify();}// 建堆private void heapify() {// 如何找到最后一个非叶子节点 size / 2 - 1,并不断往前遍历for (int i = size / 2 - 1; i >= 0; i--) {down(i);}}// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大private void down(int parent) {//找到左孩子坐标int left = parent * 2 + 1;//找到右孩子坐标int right = left + 1;int max = parent;if (left < size && array[left] > array[max]) {max = left;}if (right < size && array[right] > array[max]) {max = right;}if (max != parent) { // 找到了更大的孩子swap(max, parent);down(max);}}// 交换两个索引处的元素private void swap(int i, int j) {int t = array[i];array[i] = array[j];array[j] = t;}public static void main(String[] args) {int[] array = {1, 2, 3, 4, 5, 6, 7};MaxHeap maxHeap = new MaxHeap(array);System.out.println(Arrays.toString(maxHeap.array));}
}
3.小顶堆
public class MinHeap {int[] array;int size;public MinHeap(int capacity) {this.array = new int[capacity];}public boolean isFull() {return size == array.length;}/*** 获取堆顶元素** @return 堆顶元素*/public int peek() {return array[0];}/*** 删除堆顶元素** @return 堆顶元素*/public int poll() {int top = array[0];swap(0, size - 1);size--;down(0);return top;}/*** 删除指定索引处元素** @param index 索引* @return 被删除元素*/public int poll(int index) {int deleted = array[index];swap(index, size - 1);size--;down(index);return deleted;}/*** 替换堆顶元素** @param replaced 新元素*/public void replace(int replaced) {array[0] = replaced;down(0);}/*** 堆的尾部添加元素** @param offered 新元素* @return 是否添加成功*/public boolean offer(int offered) {if (size == array.length) {return false;}up(offered);size++;return true;}// 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶private void up(int offered) {int child = size;while (child > 0) {int parent = (child - 1) / 2;if (offered < array[parent]) {array[child] = array[parent];} else {break;}child = parent;}array[child] = offered;}public MinHeap(int[] array) {this.array = array;this.size = array.length;heapify();}// 建堆private void heapify() {// 如何找到最后这个非叶子节点 size / 2 - 1for (int i = size / 2 - 1; i >= 0; i--) {down(i);}}// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大private void down(int parent) {int left = parent * 2 + 1;int right = left + 1;int min = parent;if (left < size && array[left] < array[min]) {min = left;}if (right < size && array[right] < array[min]) {min = right;}if (min != parent) { // 找到了更大的孩子swap(min, parent);down(min);}}// 交换两个索引处的元素private void swap(int i, int j) {int t = array[i];array[i] = array[j];array[j] = t;}
}
4.JDK 的优先队列
// 大顶堆
private PriorityQueue<Integer> left = new PriorityQueue<>( (a, b) -> b-a);
// 默认是小顶堆
private PriorityQueue<Integer> right = new PriorityQueue<>();
5.建堆
- 找到最后一个非叶子节点
- 从后向前,对每个节点执行下潜
一些规律
- 一棵满二叉树节点个数为 2 h − 1 2^h-1 2h−1,如下例中高度 h = 3 h=3 h=3 节点数是 2 3 − 1 = 7 2^3-1=7 23−1=7
- 非叶子节点范围为 [ 0 , s i z e / 2 − 1 ] [0, size/2-1] [0,size/2−1]
算法时间复杂度分析

下面看交换次数的推导:设节点高度为 3
| 本层节点数 | 高度 | 下潜最多交换次数(高度-1) | |
|---|---|---|---|
| 4567 这层 | 4 | 1 | 0 |
| 23 这层 | 2 | 2 | 1 |
| 1 这层 | 1 | 3 | 2 |
每一层的交换次数为: 节点个数 ∗ 此节点交换次数 节点个数*此节点交换次数 节点个数∗此节点交换次数,总的交换次数为
$$
\begin{aligned}
& 4 * 0 + 2 * 1 + 1 * 2 \
& \frac{8}{2}*0 + \frac{8}{4}*1 + \frac{8}{8}*2 \
& \frac{8}{2^1}*0 + \frac{8}{2^2}*1 + \frac{8}{2^3}*2\
\end{aligned}
$$
即
∑ i = 1 h ( 2 h 2 i ∗ ( i − 1 ) ) \sum_{i=1}^{h}(\frac{2^h}{2^i}*(i-1)) i=1∑h(2i2h∗(i−1))
在 https://www.wolframalpha.com/ 输入
Sum[\(40)Divide[Power[2,x],Power[2,i]]*\(40)i-1\(41)\(41),{i,1,x}]
推导出
2 h − h − 1 2^h -h -1 2h−h−1
其中 2 h ≈ n 2^h \approx n 2h≈n, h ≈ log 2 n h \approx \log_2{n} h≈log2n,因此有时间复杂度 O ( n ) O(n) O(n)
二.堆题目
1.堆排序
算法描述
- heapify 建立大顶堆
- 将堆顶与堆底交换(最大元素被交换到堆底),缩小并下潜调整堆
- 重复第二步直至堆里剩一个元素
可以使用之前课堂例题的大顶堆来实现
int[] array = {1, 2, 3, 4, 5, 6, 7};
MaxHeap maxHeap = new MaxHeap(array);
System.out.println(Arrays.toString(maxHeap.array));
//判断堆的剩余元素个数
while (maxHeap.size > 1) {//交换堆顶和堆底,把最大的移到堆底maxHeap.swap(0, maxHeap.size - 1);//将堆底的元素排除maxHeap.size--;//堆顶的元素需要下沉maxHeap.down(0);
}
System.out.println(Arrays.toString(maxHeap.array));
2.数组中第 K 大元素-力扣 215 题
小顶堆(可删去用不到代码)
class MinHeap {int[] array;int size;public MinHeap(int capacity) {array = new int[capacity];}private void heapify() {for (int i = (size >> 1) - 1; i >= 0; i--) {down(i);}}public int poll() {swap(0, size - 1);size--;down(0);return array[size];}public int poll(int index) {swap(index, size - 1);size--;down(index);return array[size];}public int peek() {return array[0];}public boolean offer(int offered) {if (size == array.length) {return false;}up(offered);size++;return true;}public void replace(int replaced) {array[0] = replaced;down(0);}private void up(int offered) {int child = size;while (child > 0) {int parent = (child - 1) >> 1;if (offered < array[parent]) {array[child] = array[parent];} else {break;}child = parent;}array[child] = offered;}private void down(int parent) {int left = (parent << 1) + 1;int right = left + 1;int min = parent;if (left < size && array[left] < array[min]) {min = left;}if (right < size && array[right] < array[min]) {min = right;}if (min != parent) {swap(min, parent);down(min);}}// 交换两个索引处的元素private void swap(int i, int j) {int t = array[i];array[i] = array[j];array[j] = t;}
}
题解 1
public int findKthLargest(int[] numbers, int k) {MinHeap heap = new MinHeap(k);for (int i = 0; i < k; i++) {heap.offer(numbers[i]);}for (int i = k; i < numbers.length; i++) {if(numbers[i] > heap.peek()){heap.replace(numbers[i]);}}return heap.peek();
}
求数组中的第 K 大元素,使用堆并不是最佳选择,可以采用快速选择算法
题解 2
public int findKthLargest(int[] numbers, int k) {//小顶堆,先加入2个PriorityQueue<Integer> queue = new PriorityQueue<>();for (int i = 0; i < k; i++) {queue.add(numbers[i]);}//再加入后面剩下的for (int i = k; i < numbers.length; i++) {if (numbers[i] > queue.peek()) {queue.poll();queue.add(numbers[i]);}}return queue.peek();
}
3.数据流中第 K 大元素-力扣 703 题
上题的小顶堆加一个方法
class MinHeap {// ...public boolean isFull() {return size == array.length;}
}
题解 1
class KthLargest {private MinHeap heap;public KthLargest(int k, int[] nums) {heap = new MinHeap(k);for(int i = 0; i < nums.length; i++) {add(nums[i]);}}public int add(int val) {if(!heap.isFull()){heap.offer(val);} else if(val > heap.peek()){heap.replace(val);}return heap.peek();}}
求数据流中的第 K 大元素,使用堆最合适不过
题解 2
private PriorityQueue<Integer> queue;
private int k = 0;public E03Leetcode703_02(int k, int[] nums) {this.k = k;queue = new PriorityQueue();for (int num : nums) {add(num);}
}// 此方法会被不断调用, 模拟数据流中新来的元素
public int add(int val) {if (queue.size() < k) {queue.offer(val);} else if (queue.peek() < val) {queue.poll();queue.offer(val);}return queue.peek();
}
4.数据流的中位数-力扣 295 题
可以扩容的 heap, max 用于指定是大顶堆还是小顶堆
public class Heap {int[] array;int size;boolean max;public int size() {return size;}public Heap(int capacity, boolean max) {this.array = new int[capacity];this.max = max;}/*** 获取堆顶元素** @return 堆顶元素*/public int peek() {return array[0];}/*** 删除堆顶元素** @return 堆顶元素*/public int poll() {int top = array[0];swap(0, size - 1);size--;down(0);return top;}/*** 删除指定索引处元素** @param index 索引* @return 被删除元素*/public int poll(int index) {int deleted = array[index];swap(index, size - 1);size--;down(index);return deleted;}/*** 替换堆顶元素** @param replaced 新元素*/public void replace(int replaced) {array[0] = replaced;down(0);}/*** 堆的尾部添加元素** @param offered 新元素*/public void offer(int offered) {if (size == array.length) {grow();}up(offered);size++;}private void grow() {int capacity = size + (size >> 1);int[] newArray = new int[capacity];System.arraycopy(array, 0,newArray, 0, size);array = newArray;}// 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶private void up(int offered) {int child = size;while (child > 0) {int parent = (child - 1) / 2;boolean cmp = max ? offered > array[parent] : offered < array[parent];if (cmp) {array[child] = array[parent];} else {break;}child = parent;}array[child] = offered;}public Heap(int[] array, boolean max) {this.array = array;this.size = array.length;this.max = max;heapify();}// 建堆private void heapify() {// 如何找到最后这个非叶子节点 size / 2 - 1for (int i = size / 2 - 1; i >= 0; i--) {down(i);}}// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大private void down(int parent) {int left = parent * 2 + 1;int right = left + 1;int min = parent;if (left < size && (max ? array[left] > array[min] : array[left] < array[min])) {min = left;}if (right < size && (max ? array[right] > array[min] : array[right] < array[min])) {min = right;}if (min != parent) { // 找到了更大的孩子swap(min, parent);down(min);}}// 交换两个索引处的元素private void swap(int i, int j) {int t = array[i];array[i] = array[j];array[j] = t;}
}
题解 1
private Heap left = new Heap(10, false);
private Heap right = new Heap(10, true);/**为了保证两边数据量的平衡<ul><li>两边数据一样时,加入左边</li><li>两边数据不一样时,加入右边</li></ul>但是, 随便一个数能直接加入吗?<ul><li>加入左边前, 应该挑右边最小的加入</li><li>加入右边前, 应该挑左边最大的加入</li></ul>*/
public void addNum(int num) {if (left.size() == right.size()) {right.offer(num);left.offer(right.poll());} else {left.offer(num);right.offer(left.poll());}
}/*** <ul>* <li>两边数据一致, 左右各取堆顶元素求平均</li>* <li>左边多一个, 取左边元素</li>* </ul>*/
public double findMedian() {if (left.size() == right.size()) {return (left.peek() + right.peek()) / 2.0;} else {return left.peek();}
}
本题还可以使用平衡二叉搜索树求解,不过代码比两个堆复杂
题解 2
/*** 为了保证两边数据量的平衡* <ul>* <li>两边个数一样时,左边个数加一</li>* <li>两边个数不一样时,右边个数加一</li>* </ul>* 但是, 随便一个数能直接加入吗?* <ul>* <li>左边个数加一时, 把新元素加在右边,弹出右边最小的加入左边</li>* <li>右边个数加一时, 把新元素加在左边,弹出左边最小的加入右边</li>* </ul>*/
public void addNum(int num) {if (left.size() == right.size()) {right.offer(num);left.offer(right.poll());} else {left.offer(num);right.offer(left.poll());}
}/*** <ul>* <li>两边数据一致, 左右各取堆顶元素求平均</li>* <li>左边多一个, 取左边堆顶元素</li>* </ul>*/
public double findMedian() {if (left.size() == right.size()) {return (left.peek() + right.peek()) / 2.0;} else {return left.peek();}
}// 大顶堆
private PriorityQueue<Integer> left = new PriorityQueue<>((a, b) -> Integer.compare(b, a)
);
// 默认是小顶堆
private PriorityQueue<Integer> right = new PriorityQueue<>();
觉得有用的话点个赞
👍🏻呗。
❤️❤️❤️本人水平有限,如有纰漏,欢迎各位大佬评论批评指正!😄😄😄💘💘💘如果觉得这篇文对你有帮助的话,也请给个点赞、收藏下吧,非常感谢!👍 👍 👍
🔥🔥🔥Stay Hungry Stay Foolish 道阻且长,行则将至,让我们一起加油吧!🌙🌙🌙
相关文章:

【数据结构-堆】堆
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学…...

Ansible 自动化运维工具部署主从数据库+读写分离
文章目录 Ansible 自动化运维工具部署主从数据库读写分离一、主从复制和读写分离介绍二、准备工作(1)节点规划(2)修改主机名(3)免密(4)配置IP映射(5)安装ansi…...
)
蓝桥杯官网填空题(星期几)
题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 1949 年的国庆节( 10 月 1 日)是星期六。 今年(2012)的国庆节是星期一。 那么,从建国到现在࿰…...
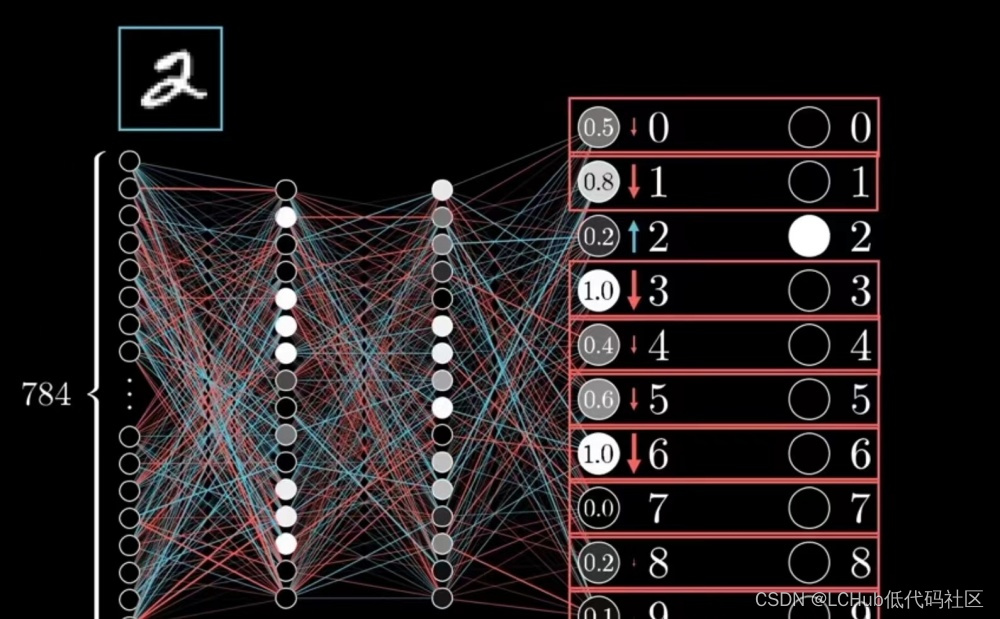
《向量数据库指南》——向量数据库会是 AI 的“iPhone 时刻”吗?
最近一年,以 ChatGPT、LLaMA 为代表的大语言模型的兴起,将向量数据库的发展推向了新的高度。 向量数据库是一种在机器学习和人工智能领域日益流行的新型数据库,它能够帮助支持基于神经网络而不是关键字的新型搜索引擎。向量数据库不同于传统的关系型数据库,例如 PostgreSQ…...
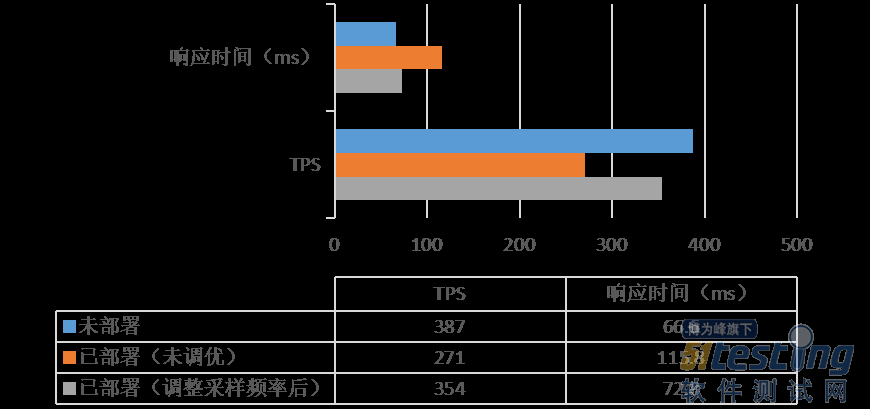
案例实践丨基于SkyWalking全链路监控的微服务系统性能调优实践篇
1背景 随着开源社区和云计算的快速推进,云原生微服务作为新型应用系统的核心架构,得到了越来越广泛的应用。根据Gartner对微服务的定义:“微服务是范围狭窄、封装紧密、松散耦合、可独立部署且可独立伸缩的应用程序组件。” 微服务之父&…...
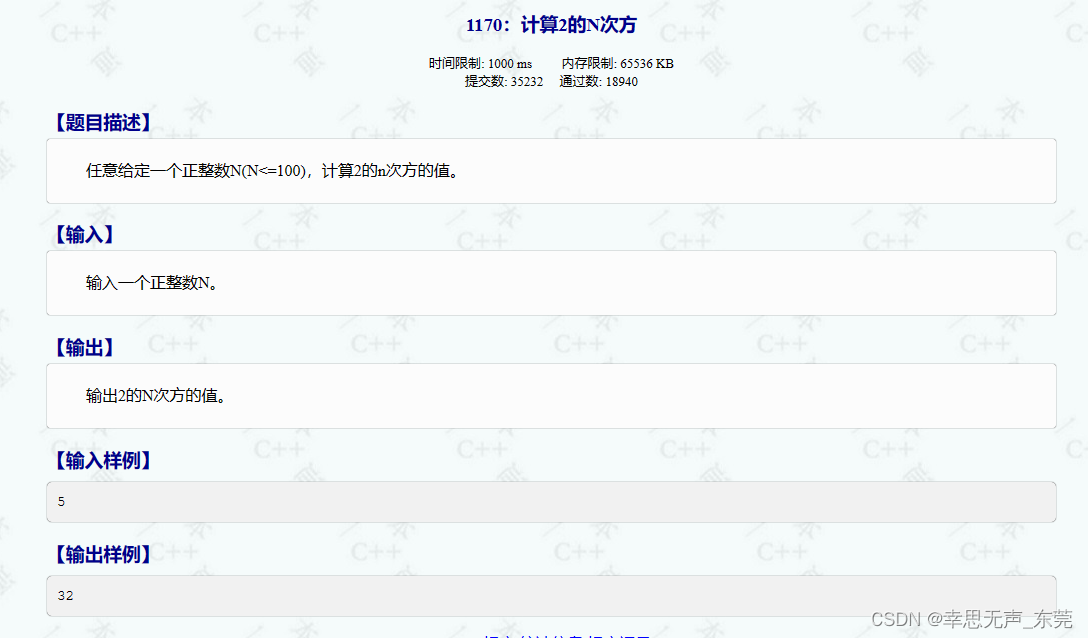
C++信息学奥赛1170:计算2的N次方
#include <iostream> #include <string> #include <cstring>using namespace std;int main() {int n;cin >> n; // 输入一个整数nint arr[100];memset(arr, -1, sizeof(arr)); // 将数组arr的元素初始化为-1,sizeof(arr)表示arr数组的字节…...

windos本地文件上传到ubuntu
如何把本地文件放到服务器上 scp /path/to/local/file usernameserver:/path/to/remote/directoryusernameserver 是服务器名和IP...

做软件测试,掌握哪些技术才能算作“测试大佬”?
一、过硬的基础能力 其实所有的测试大佬都是从底层基础开始的,随着时间,经验的积累慢慢变成大佬。要想稳扎稳打在测试行业深耕,成为测试大牛,首当其冲的肯定就是拥有过硬的基础,所有的基础都是根基,后期所有…...

【算法与数据结构】530、LeetCode二叉搜索树的最小绝对差
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:二叉搜索树的性质是左子树的所有节点键值小于中间节点键值,右子树的所有节点键值大于中间节…...

input输入事件
我要实现input输入框一边输入,一边在控制台输出结果 现有如下代码 <body><input type"text" onchange"myFunction()" /><script>function myFunction(){console.log(999)}</script> </body> 当敲下回车键后才会…...
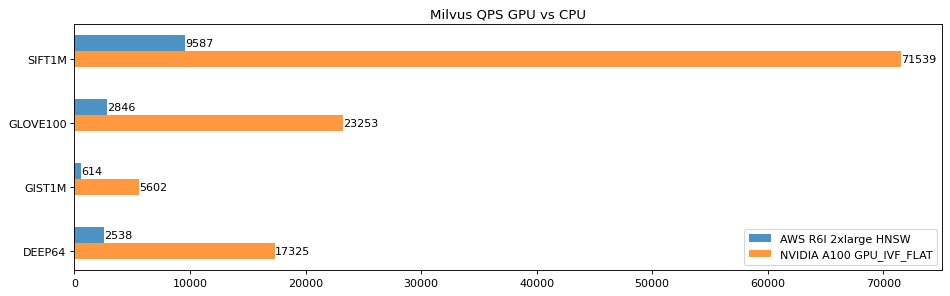
接入 NVIDIA A100、吞吐量提高 10 倍!Milvus GPU 版本使用指南
Milvus 2.3 正式支持 NVIDIA A100! 作为为数不多的支持 GPU 的向量数据库产品,Milvus 2.3 在吞吐量和低延迟方面都带来了显著的变化,尤其是与此前的 CPU 版本相比,不仅吞吐量提高了 10 倍,还能将延迟控制在极低的水准。…...
php://filter协议在任意文件读取漏洞(附例题)
php://filter php://fiter 中文叫 元器封装,咱也不知道为什么这么翻译,目前我的理解是可以通过这个玩意对上面提到的php IO流进行处理,及现在可以对php的 IO流进行一定操作。 过滤器:及通过php://filter 对php 的IO流进行的具体…...
【Redis】1、NoSQL之Redis的配置及优化
关系数据库与非关系数据库 关系型数据库 关系型数据库是一个结构化的数据库,创建在关系模型(二维表格模型)基础上,一般面向于记录。 SQL 语句(标准数据查询语言)就是一种基于关系型数据库的语言&a…...

9.5QTday6作业
面试题1:c语言中的static和c中的static的用法 在c语言中: 1.static修饰的全局变量作用域限制在当前文件,无法被外部文件所引用。2.static修饰的局部变量延长生命周期,但不改变作用域,同样无法被外部文件所引用。3.st…...
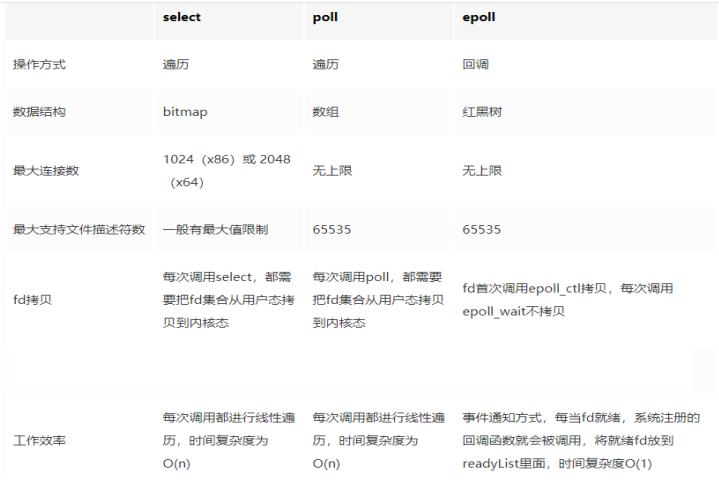
Redis I/O多路复用机制
一、基础回顾 1.1 多路复用要解决什么问题 并发多客户端连接场景,在多路复用之前最简单和典型的方案就是同步阻塞网络IO模型。 这种模式的特点就是用一个进程来处理一个网络连接(一个用户请求),比如一段典型的示例代码如下。 直接调用 recv 函数从一个 socket 上…...

Matlab 2016安装MinGW-w64-4.9.2
Matlab 2016安装MinGW-w64-4.9.2 项目需求:需要将matlab中的.m文件编译为cpp文件 .dll .h .lib。 我相信大家在对matlab2016安装MinGW-w64出现了各种各样的问题。如:4.9.2安装失败;安装了其他版本但是matlab检测不到,或者其他各种…...
Tomcat配置ssl、jar包
Tomcat配置ssl 部署tomcat服务,项目做到用https访问,使用nginx去做,访问任意一个子网站,都是https 或者 医美项目需要 上传jdk 456 tomcat war包 [nginx-stable] namenginx stable repo baseurlhttp://nginx.org/packages/…...

Unity中Shader实现UI去色功能的实现思路
文章目录 前言一、在开发过程中,在UI中会涉及一些需要置灰UI的需求,有很多实现的方法1、做两套纹理,通过程序控制切换2、使用shader实现对纹理去色 二、这里主要记录用shader实现的思路1、基础纹理的采样2、支持组件中的调色3、遮罩功能4、去…...

Python垃圾回收机制详解:引用计数与循环垃圾收集器
文章目录 Python垃圾回收机制引用计数机制循环垃圾收集器小结详细讲解及实操1. 程序中的垃圾问题2. 垃圾的定义3. 自动垃圾回收机制4. 示例:使用del方法删除垃圾对象5. 手动处理垃圾回收6. 结束程序7. 垃圾回收的自动处理8. 结束程序 python精品专栏推荐python基础知…...
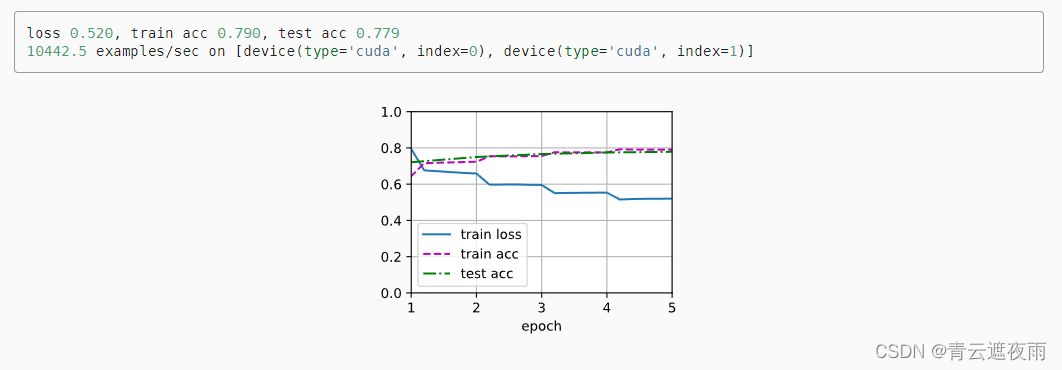
自然语言处理应用(三):微调BERT
微调BERT 微调(Fine-tuning)BERT是指在预训练的BERT模型基础上,使用特定领域或任务相关的数据对其进行进一步训练以适应具体任务的需求。BERT(Bidirectional Encoder Representations from Transformers)是一种基于Tr…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...
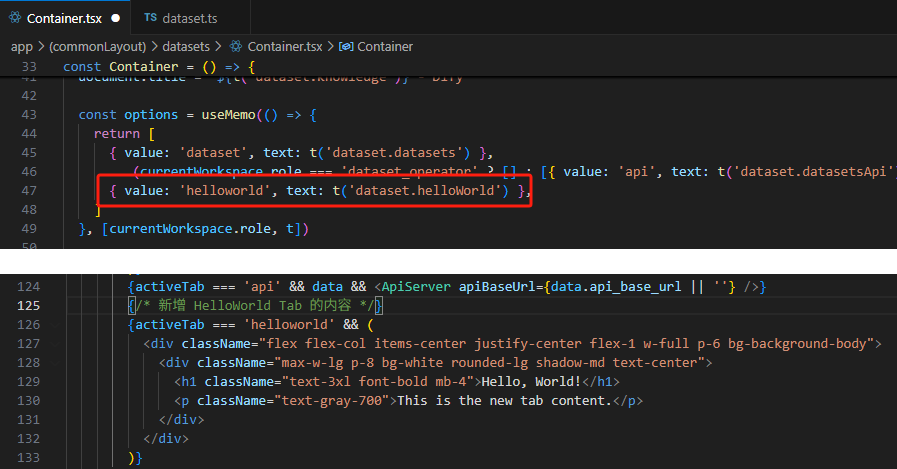
【技巧】dify前端源代码修改第一弹-增加tab页
回到目录 【技巧】dify前端源代码修改第一弹-增加tab页 尝试修改dify的前端源代码,在知识库增加一个tab页"HELLO WORLD",完成后的效果如下 [gif01] 1. 前端代码进入调试模式 参考 【部署】win10的wsl环境下启动dify的web前端服务 启动调试…...

【Zephyr 系列 16】构建 BLE + LoRa 协同通信系统:网关转发与混合调度实战
🧠关键词:Zephyr、BLE、LoRa、混合通信、事件驱动、网关中继、低功耗调度 📌面向读者:希望将 BLE 和 LoRa 结合应用于资产追踪、环境监测、远程数据采集等场景的开发者 📊篇幅预计:5300+ 字 🧭 背景与需求 在许多 IoT 项目中,单一通信方式往往难以兼顾近场数据采集…...

【字节拥抱开源】字节团队开源视频模型 ContentV: 有限算力下的视频生成模型高效训练
本项目提出了ContentV框架,通过三项关键创新高效加速基于DiT的视频生成模型训练: 极简架构设计,最大化复用预训练图像生成模型进行视频合成系统化的多阶段训练策略,利用流匹配技术提升效率经济高效的人类反馈强化学习框架&#x…...

