树和二叉树的相关概念及结构
目录
1.树的概念及结构
1.1 树的概念
1.2 树的相关概念
1.3 树的表示
1.3.1 孩子兄弟表示法
1.3.2 双亲表示法
1.4 树的实际应用
2.二叉树的概念及结构
2.1 二叉树的概念
2.2 特殊的二叉树
2.3 二叉树的性质
2.4 二叉树的存储
2.4.1 顺序存储
2.4.2 链式存储
1.树的概念及结构
1.1 树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根结点,根节点没有前驱结点
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 因此,树是递归定义的
1.2 树的相关概念

节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林;
1.3 树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系。
我们先看下面两种存储方式:
//方式1
struct TreeNode
{int val;struct TreeNode* child1;struct TreeNode* child2;struct TreeNode* child3;struct TreeNode* child4;//...
}
//方式二
#define N 3 //N是树的度struct TreeNode
{int val;struct TreeNode* childArr[N];
}
显然上面两种方式都存在一定缺陷:
结点的度不固定,方式一就不能使用;方式二的指针数组有可能存在空间浪费。
1.3.1 孩子兄弟表示法
在所有表示方法中,有一个最优解,那就是孩子兄弟表示法。
typedef int DataType;struct Node
{struct Node* firstChild; // 第一个孩子结点struct Node* nextBrother; // 指向其下一个兄弟结点DataType data; // 结点中的数据域
};
孩子是第一个孩子,兄弟是下一个兄弟。

这个最优解还可以遍历树中某个结点的所有孩子:
TreeNode* Node;
TreeNode* child = Node->firstChild;
while(child)
{printf("%d ", child->val);child = child->nextBrother;
}
1.3.2 双亲表示法

- 双亲表示法用一个数组存储双亲的下标或者指针。
- 根结点双亲的下标默认为-1。
- 判断两个节点是否在同一棵树:找根,是同一个根就在同一棵树。
1.4 树的实际应用
文件系统的目录树结构:

2.二叉树的概念及结构
2.1 二叉树的概念
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵别称为左子树和右子树的二叉树组成

注意:
- 二叉树并不是所有的结点的度都为2,而是所有结点的度最大为2。
- 二叉树的左右子树不能颠倒,是一个有序树。
- 对于任意的二叉树都是由以下几种情况复合而成的:

2.2 特殊的二叉树
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

2.3 二叉树的性质
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1) 个结点.
- 对任何一棵二叉树, 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为n2 ,则有 n0=n2 +1
- 对于一颗完全二叉树,度为1的结点最多只有1个
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是 2^h-1(满二叉树)
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h= log(n+1)(ps: 是log以2为底)
- 高度为h的完全二叉树的结点个数范围:[2^(h-1) , 2^h-1]
- 结点个数为n的完全二叉树的高度:logn向下取整再加1 或者 log(n+1)向上取整
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对
于序号为i的结点有:
若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
若2i+1<n,左孩子序号:2i+1;若2i+1>=n, 无左孩子
若2i+2<n,右孩子序号:2i+2;若2i+2>=n, 无右孩子
2.4 二叉树的存储
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
2.4.1 顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。

2.4.2 链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链。
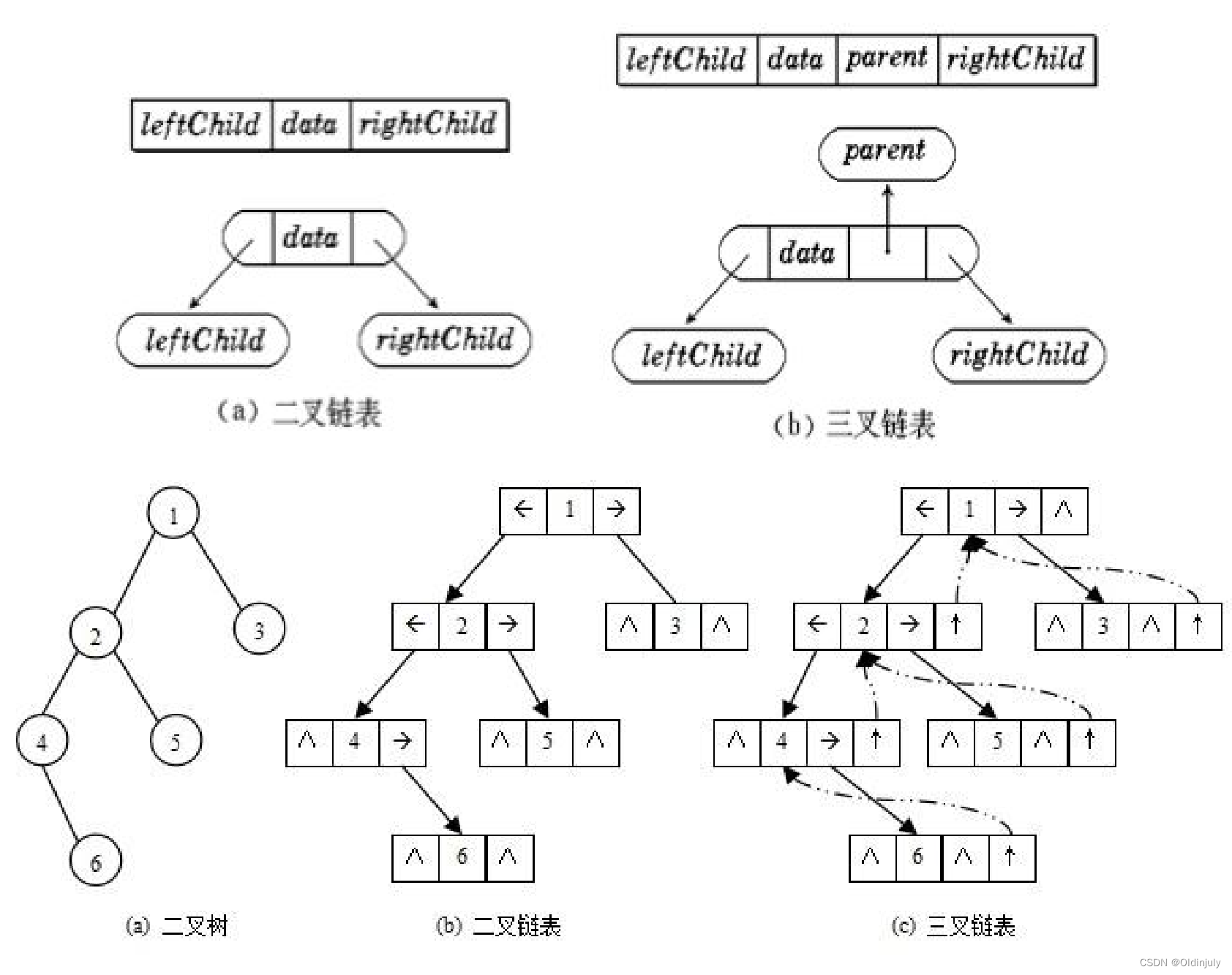
typedef char BTDataType;//二叉链表
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;//三叉链表
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* parent;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
相关文章:

树和二叉树的相关概念及结构
目录 1.树的概念及结构 1.1 树的概念 1.2 树的相关概念 1.3 树的表示 1.3.1 孩子兄弟表示法 1.3.2 双亲表示法 1.4 树的实际应用 2.二叉树的概念及结构 2.1 二叉树的概念 2.2 特殊的二叉树 2.3 二叉树的性质 2.4 二叉树的存储 2.4.1 顺序存储 2.4.2 链式存储 1.树…...
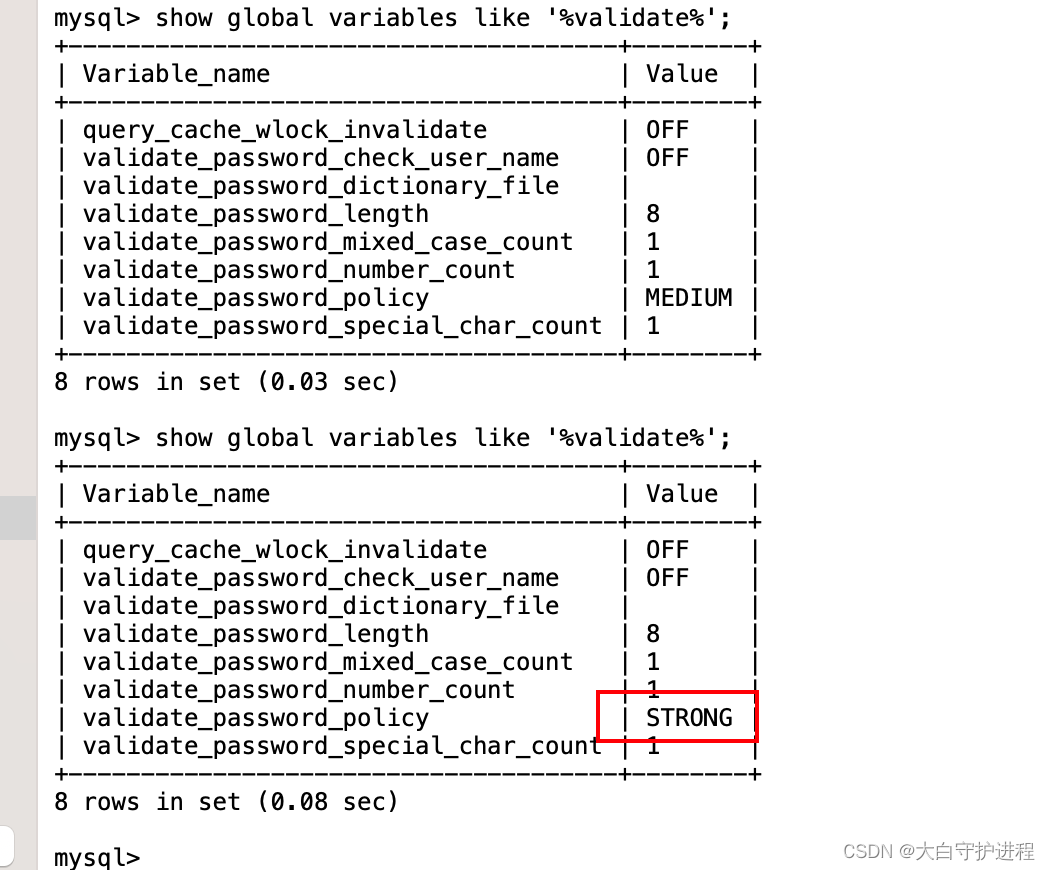
MySQL安装validate_password_policy插件
功能介绍 validate_password_policy 是插件用于验证密码强度的策略。该参数可以设定三种级别:0代表低,1代表中,2代表高。 validate_password_policy 主要影响密码的强度检查级别: 0/LOW:只检查密码长度。 1/MEDIUM&am…...

数据在内存中的存储——练习3
题目: 3.1 #include <stdio.h> int main() {char a -128;printf("%u\n",a);return 0; }3.2 #include <stdio.h> int main() {char a 128;printf("%u\n",a);return 0; }思路分析: 首先二者极其相似%u是无符号格式进行…...

web-案例
分页插件 登录 事务...
第一章 JAVA入门
文章目录 1.2 Java 的特点1.2.1 简单1.2.2 面向对象1.2.3 与平台无关① 平台与机器指令② C/C程序依赖平台③ Java 虚拟机与字节码1.2.4 多线程1.2.5 动态1.30安装 JDK1.3.1 平台简介0 Java SE②Java EE1.4 Java 程序的开发步骤②保存源文件1.5.2 编译1.8 Java之父-James Gosli…...
二叉树详解(求二叉树的结点个数、深度、第k层的个数、遍历等)
二叉树,是一种特殊的树,特点是树的度小于等于2(树的度是整个树的结点的度的最大值),由于该特性,构建二叉树的结点只有三个成员,结点的值和指向结点左、右子树的指针。 typedef int DateType; t…...

Apollo配置中心及Python连接
本文将会介绍如何启动Apollo,在Apollo中配置参数,以及如何使用Python连接Apollo. Apollo介绍 在文章Python之读取配置文件和文章Python之配置文件处理中,笔者分别介绍了如何使用Python来处理ini, yaml, conf等配置文件。这种配置方式比较方便…...
--audio - 多媒体音频)
LuatOS-SOC接口文档(air780E)--audio - 多媒体音频
常量 常量 类型 解释 audio.PCM number PCM格式,即原始ADC数据 audio.MORE_DATA number audio.on回调函数传入参数的值,表示底层播放完一段数据,可以传入更多数据 audio.DONE number audio.on回调函数传入参数的值,表示…...
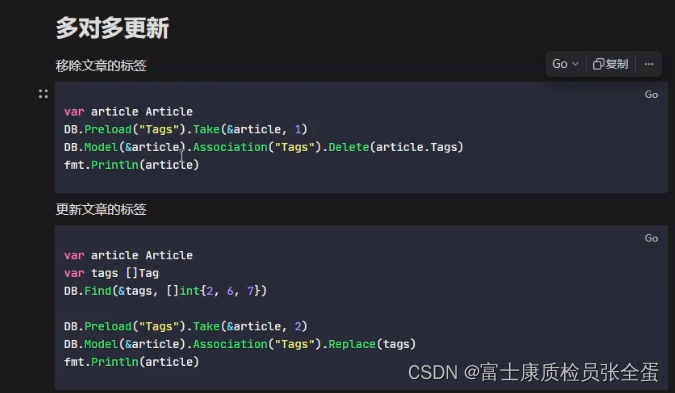
Golang gorm manytomany 多对多 更新、删除、替换
Delete 移除 只删除中间表的数据 删除原有的 var a Article1db.Preload("Tag1s").Take(&a, 1)fmt.Printf("%v", a) {1 k8s [{1 cloud []} {2 linux []}]}mysql> select * from article1; ------------ | id | title | ------------ | 1 | k8s …...
:串口驱动模块uart_drive、例化uart_rx、uart_tx)
FPGA-结合协议时序实现UART收发器(四):串口驱动模块uart_drive、例化uart_rx、uart_tx
FPGA-结合协议时序实现UART收发器(四):串口驱动模块uart_drive、例化uart_rx、uart_tx 串口驱动模块uart_drive、例化uart_rx、uart_tx,功能实现 文章目录 FPGA-结合协议时序实现UART收发器(四)࿱…...

Transformers-Bert家族系列算法汇总
🤗 Transformers 提供 API 和工具,可轻松下载和训练最先进的预训练模型。使用预训练模型可以降低计算成本、碳足迹,并节省从头开始训练模型所需的时间和资源。这些模型支持不同形式的常见任务,例如: 📝 自…...
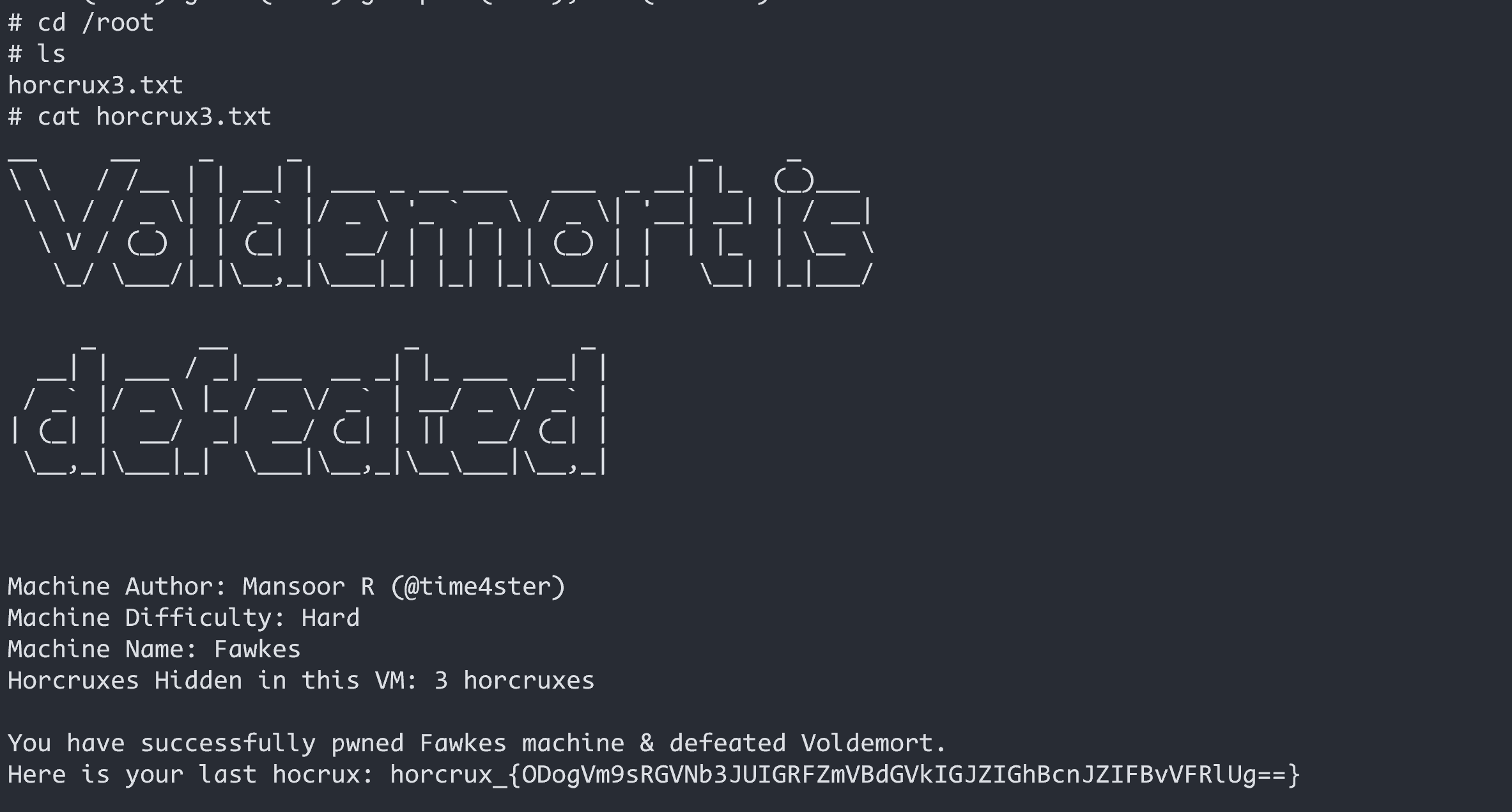
Vulnhub系列靶机---HarryPotter-Fawkes-哈利波特系列靶机-3
文章目录 信息收集主机发现端口扫描dirsearch扫描gobuster扫描 漏洞利用缓冲区溢出edb-debugger工具msf-pattern工具 docker容器内提权tcpdump流量分析容器外- sudo漏洞提权 靶机文档:HarryPotter: Fawkes 下载地址:Download (Mirror) 难易程度ÿ…...
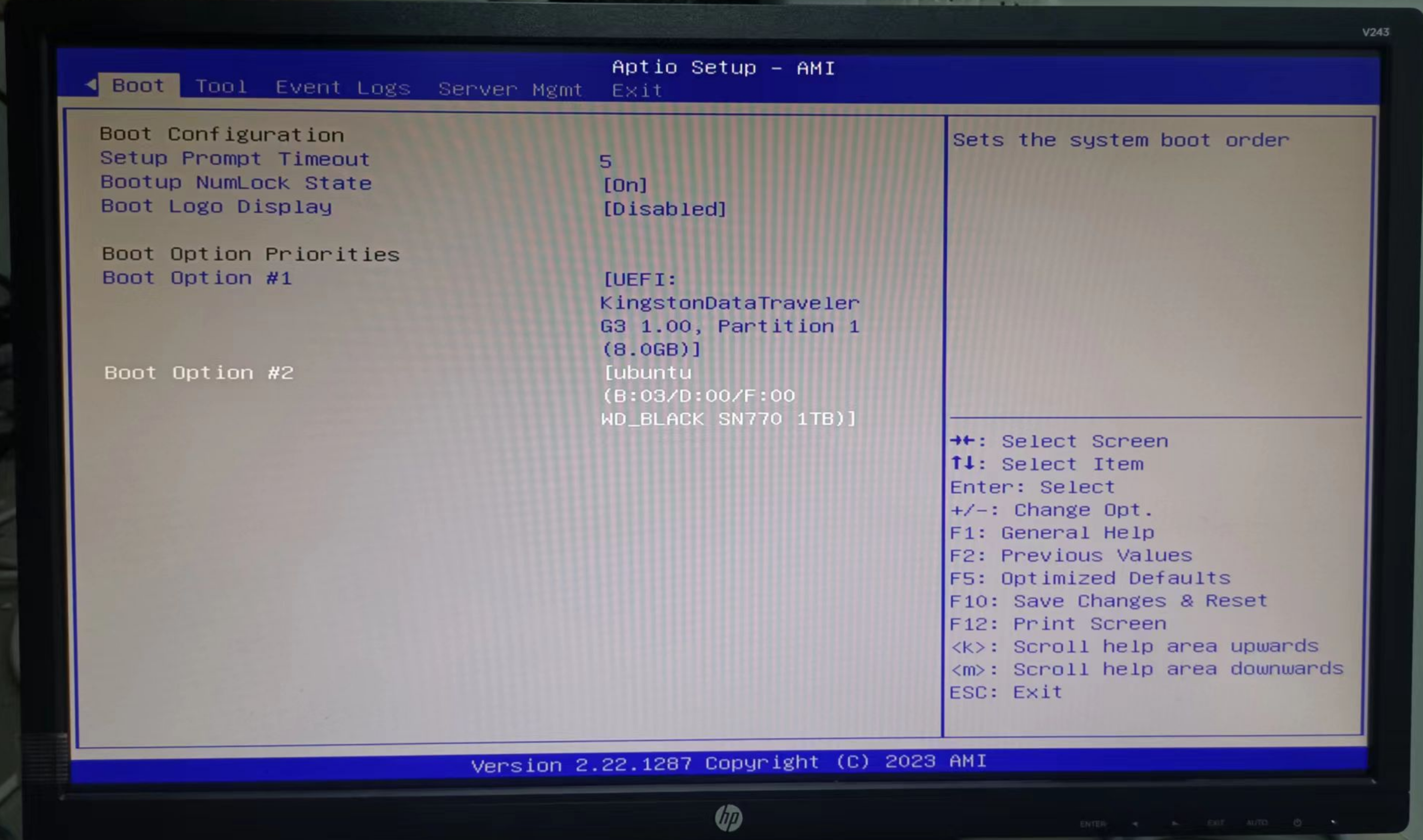
【服务器】ASUS ESC4000-E11 安装系统
ASUS ESC4000-E11说明书 没找到 ASUS ESC4000-E11的说明书,下面是ESC4000A-E11的说明书: https://manualzz.com/doc/65032674/asus-esc4000a-e11-servers-and-workstation-user-manual 下载地址: https://www.manualslib.com/manual/231379…...
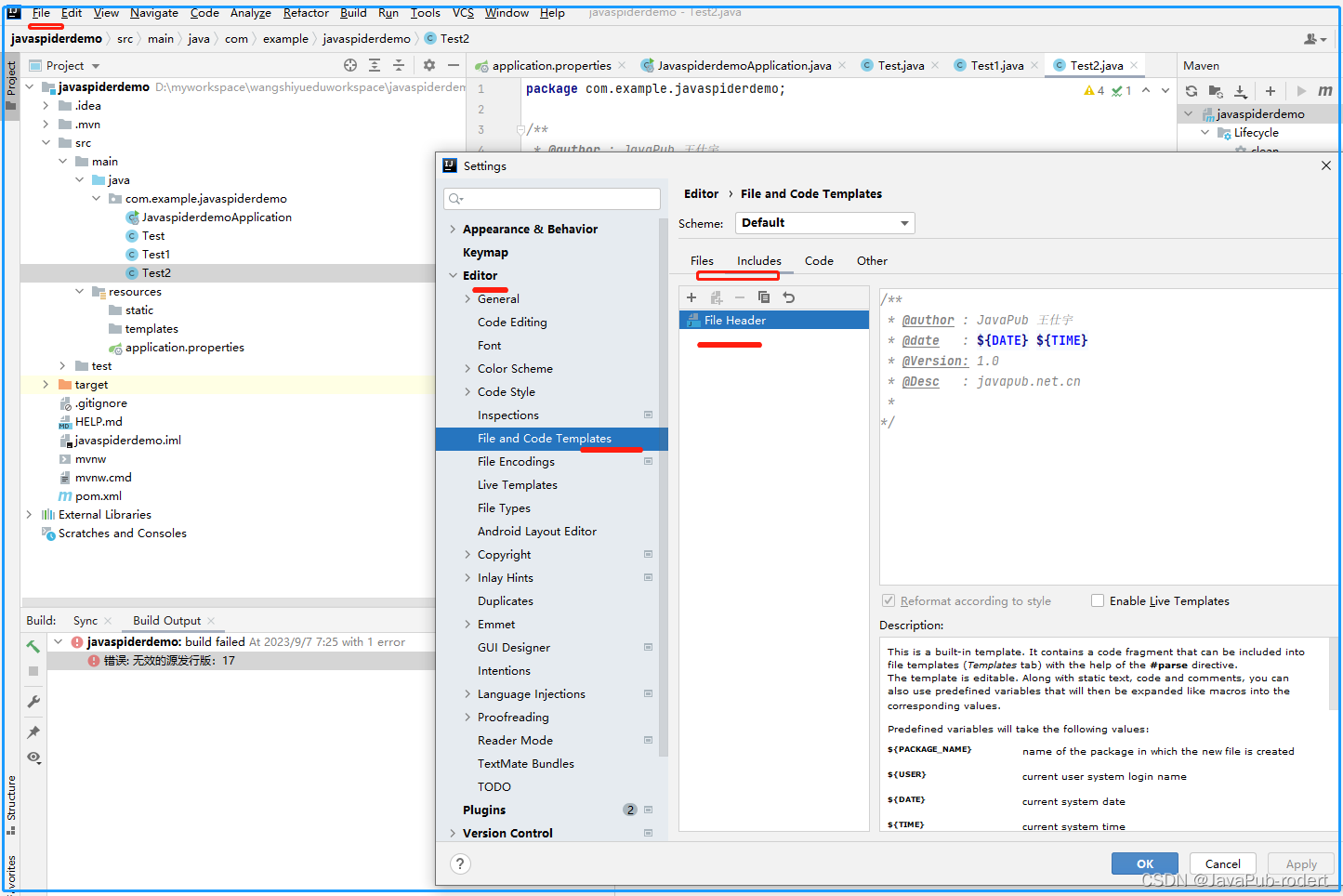
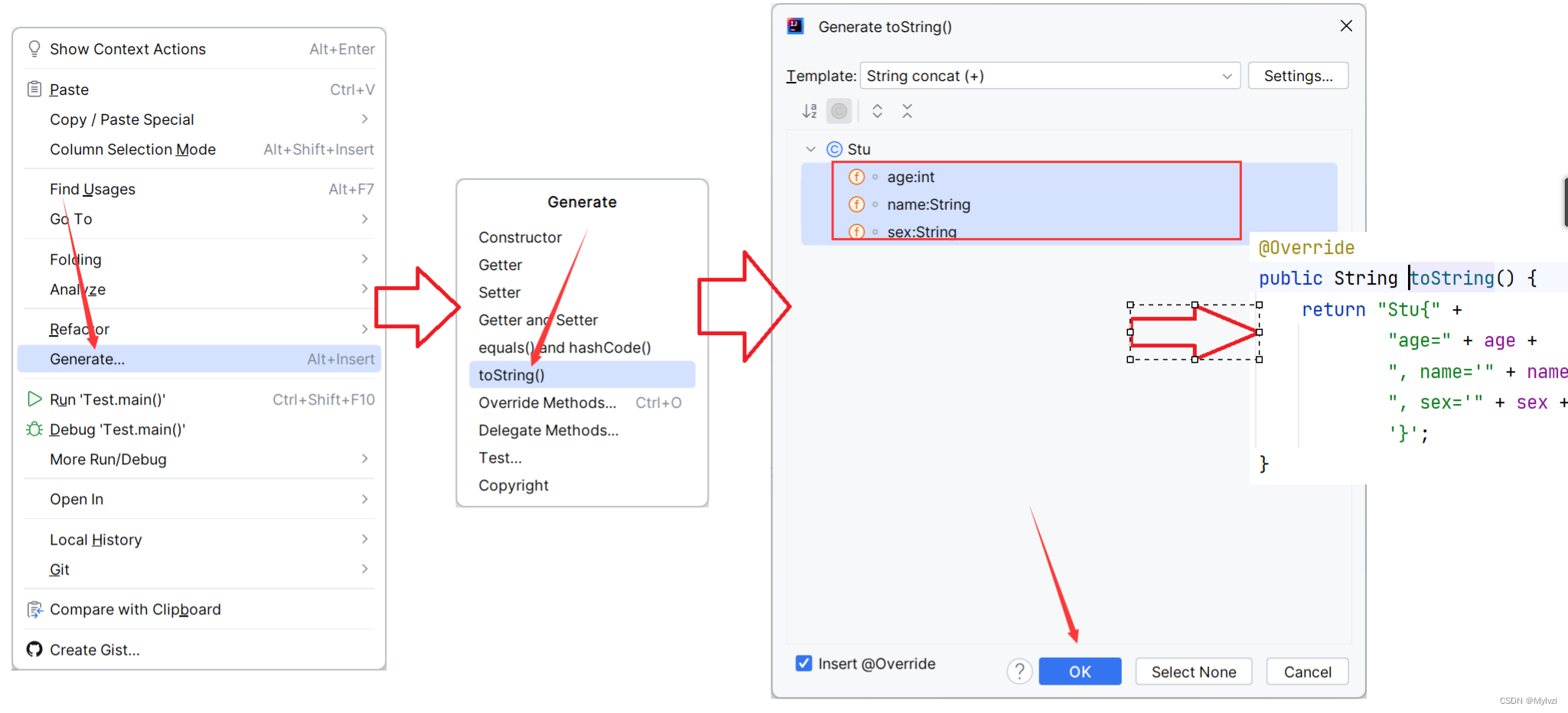
创建java文件 自动添加作者、时间等信息 – IDEA 技巧
2023 09 亲测 文章目录 效果修改位置配置信息 效果 每次创建文件的时候,自动加上作者、时间等信息 修改位置 打开:File —> Settings —> Editor —> File and Code Templates —> includes —> FileHeader 配置信息 /*** author : Java…...
第27章_瑞萨MCU零基础入门系列教程之freeRTOS实验
本教程基于韦东山百问网出的 DShanMCU-RA6M5开发板 进行编写,需要的同学可以在这里获取: https://item.taobao.com/item.htm?id728461040949 配套资料获取:https://renesas-docs.100ask.net 瑞萨MCU零基础入门系列教程汇总: ht…...
Java学习之--类和对象
💕粗缯大布裹生涯,腹有诗书气自华💕 作者:Mylvzi 文章主要内容:Java学习之--类和对象 类和对象 类的实例化: 1.什么叫做类的实例化 利用类创建一个具体的对象就叫做类的实例化! 当我们创建了…...

Unity技术手册-UGUI零基础详细教程-Canvas详解
点击跳转专栏>Unity3D特效百例点击跳转专栏>案例项目实战源码点击跳转专栏>游戏脚本-辅助自动化点击跳转专栏>Android控件全解手册点击跳转专栏>Scratch编程案例点击跳转>软考全系列点击跳转>蓝桥系列 👉关于作者 专注于Android/Unity和各种游…...

破天荒呀!小杜微信有名额了
写在前面 小杜粉,众所周知前面加小杜微信为好友的基本都是由名额限制的。一般都是付费进入社群且进行备注,小杜才会长期保留微信好友。主要由于,添加的人数太多了,微信账号人数名额有限。因此,小杜过一段时间…...
领域驱动设计:领域模型与代码模型的一致性
文章目录 领域对象的整理从领域模型到微服务的设计领域层的领域对象应用层的领域对象 领域对象与微服务代码对象的映射典型的领域模型非典型领域模型 DDD 强调先构建领域模型然后设计微服务,以保证领域模型和微服务的一体性,因此我们不能脱离领域模型来谈…...

TypeScript命名空间和模块
🎬 岸边的风:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 ⛺️ 生活的理想,就是为了理想的生活 ! 目录 命名空间(Namespace) 命名空间(Namespace)使用场景 第三方库 兼容…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...

